建筑结构——受弯构件计算

一、构件编号: L-1二、设计依据《混凝土结构设计规范》 GB50010-2002三、计算信息1. 几何参数截面类型: 矩形截面宽度: b=200mm截面高度: h=450mm2. 材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2受拉纵筋种类: HRB400 fy=360N/mm2受压纵筋种类: HRB400 fy=360N/mm2受拉纵筋最小配筋率: ρmin=0.200％受压纵筋最小配筋率: ρ'min=0.200％受拉纵筋合力点至近边距离: as=35mm受压纵筋合力点至近边距离: as'=35mm3. 配筋信息As=942mm2A's=628mm24. 设计参数结构重要性系数: γo=1.0四、计算过程1. 验算受拉钢筋最小配筋率ρ=As/(b*h)=942/(200*450)=1.047％ρ=1.047％≥ρmin=0.200％, 满足最小配筋率要求。

2. 验算受压钢筋最小配筋率ρ'=A's/(b*h)=628/(200*450)=0.698％ρ'=0.698％≥ρ'min=0.200％, 满足最小配筋率要求。

3. 计算截面有效高度ho=h-as=450-35=415mm4. 计算混凝土受压区高度x=(fy*As-f'y*A's)/(α1*fc*b)=(360*942-360*628)/(1.0*14.3*200)=40mm5. 计算弯矩设计值2a's=2*35=70>x=40M=fy*As*(ho-a's)/γo=360*942*(415-35)/1.0=128.866kN*m一、构件编号: L-2（处理后）二、设计依据《混凝土结构设计规范》 GB50010-2002三、计算信息1. 几何参数截面类型: 矩形截面宽度: b=200mm截面高度: h=450mm2. 材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2受拉纵筋种类: HRB400 fy=360N/mm2受压纵筋种类: HRB400 fy=360N/mm2受拉纵筋最小配筋率: ρmin=0.200％受压纵筋最小配筋率: ρ'min=0.200％受拉纵筋合力点至近边距离: as=35mm受压纵筋合力点至近边距离: as'=35mm3. 配筋信息As=1239mm2A's=628mm24. 设计参数结构重要性系数: γo=1.0四、计算过程1. 验算受拉钢筋最小配筋率ρ=As/(b*h)=1239/(200*450)=1.377％ρ=1.377％≥ρmin=0.200％, 满足最小配筋率要求。

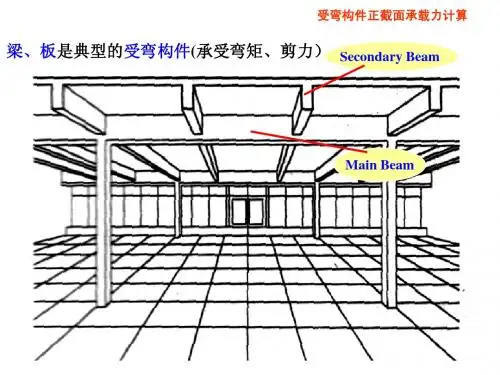
混凝土梁受弯计算方法混凝土梁是建筑结构中常见的承受荷载的构件，而受弯是梁在承受荷载作用下所发生的主要变形形式之一。

准确计算混凝土梁的受弯性能，对于工程结构的设计和施工至关重要。

在本文中，我将介绍混凝土梁受弯计算的基本方法，并分享我对这个主题的观点和理解。

1. 引言混凝土梁受弯计算方法是结构力学中的一个重要课题。

在工程实践中，设计工程师需要根据梁的几何形状、荷载条件和材料性能等参数，计算梁的受弯承载力和变形。

合理的计算方法能够保证梁的结构安全性和正常使用性能。

2. 混凝土梁受弯计算方法混凝土梁受弯计算方法主要包括弯矩计算和截面抵抗力计算两个方面。

弯矩计算是确定梁在不同截面上的弯矩大小和分布规律，而截面抵抗力计算则是确定混凝土梁在不同截面上的抗弯能力。

2.1 弯矩计算弯矩计算是混凝土梁受弯计算的第一步。

根据梁的几何形状、荷载条件和支座情况，可以通过力学原理和结构受力平衡条件来确定梁上各截面的弯矩大小和分布规律。

常用的计算方法包括弯矩图法、力矩平衡法和变位法等。

2.2 截面抵抗力计算截面抵抗力计算是混凝土梁受弯计算的第二步。

根据混凝土材料的强度和变形性能，可以确定混凝土梁在不同截面上的抗弯能力。

常用的计算方法包括弯矩-曲率法、受拉区尺寸法和变形受力法等。

在计算截面抵抗力时，需要考虑混凝土的压杆破坏、拉杆破坏和受压区剪切破坏等不同破坏模式。

3. 观点和理解对于混凝土梁受弯计算方法，我认为以下几个方面值得关注和思考：3.1 简化计算与精确计算的权衡在实际工程中，设计工程师通常需要权衡计算的精确度和计算的简化程度。

简化计算方法可以减少计算复杂度和工作量，提高设计效率。

然而，过于简化的计算方法可能导致计算结果的不准确性和梁的施工和使用安全性的隐患。

在实际应用中，设计工程师需要根据具体情况选择合适的计算方法，并考虑计算结果的安全裕度。

3.2 材料性能和设计准则的应用混凝土材料的力学性能和设计准则对于梁的受弯计算具有重要影响。

钢结构受弯构件计算4.1 梁的类型和应用钢梁在建筑结构中应用广泛，主要用于承受横向荷载。

在工业和民用建筑中，最常见的是楼盖梁、墙架梁、工作平台梁、起重机梁、檩条等。

钢梁按制作方法的不同，可分为型钢梁和组合梁两大类，如图4-1所示。

型钢梁又可分为热轧型钢梁和冷弯薄壁型钢梁。

前者常用工字钢、槽钢、H 型钢制成，如图4-1（a）、（b）、（c）所示，应用比较广泛，成本比较低廉。

其中，H 型钢截面最为合理，其翼缘内外边缘平行，与其他构件连接方便。

当荷载较小、跨度不大时可用冷弯薄壁C 型钢[图4-1（d）、（e）]或Z型钢[图4-1（f）]，可以有效节约钢材，如用作屋面檩条或墙面墙梁。

受到尺寸和规格的限制，当荷载或跨度较大时，型钢梁往往不能满足承载力或刚度的要求，这时需要用组合梁。

最常见的是用三块钢板焊接而成的H 形截面组合梁[图4-1（g）]，俗称焊接H 型钢，其构造简单，加工方便。

当所需翼缘板较厚时，可采用双层翼缘板组合梁[图4-1（h）]。

荷载很大而截面高度受到限制或对抗扭刚度要求较高时，可采用箱形截面梁[图4-1（i）]。

当梁要承受动力荷载时，由于对疲劳性能要求较高，需要采用高强度螺栓连接的H 形截面梁[图4-1（j）]。

混凝土适用于受压，钢材适用于受拉，钢与混凝土组合梁[图4-1（k）]可以充分发挥两种材料的优势，经济效果较明显。

图4-1 梁的截面形式（a）工字钢；（b）槽钢；（c）H 型钢；（d），（e）C型钢；（f）Z型钢；（g）H 形截面组合梁；（h）双层翼缘板组合梁；（i）箱形截面梁；（j）高强度螺栓连接的H 形截面梁；（k）钢与混凝土组合梁为了更好地发挥材料的性能，钢材可以做成截面沿梁长度方向变化的变截面梁。

常用的有楔形梁，这种梁仅改变腹板高度，而翼缘的厚度、宽度及腹板的厚度均不改变。

因其加工方便，经济性能较好，目前已经广泛用于轻型门式刚架房屋中。

简支梁可以在支座附近降低截面高度，除节约材料外，还可以节省净空，已广泛应用于大跨度起重机梁中，另外，还可以做成改变翼缘板的宽度或厚度的变截面梁。

【钢筋混凝土受弯构件的裂缝宽度和挠度计算】一、引言钢筋混凝土结构是现代建筑中常见的结构形式之一，而受弯构件作为其重要组成部分，其裂缝宽度和挠度的计算是设计过程中的关键内容。

在本文中，我将分析钢筋混凝土受弯构件的裂缝宽度和挠度计算，并对其进行深度探讨，希望能为您提供有价值的信息。

二、裂缝宽度计算1.裂缝宽度计算公式钢筋混凝土受弯构件的裂缝宽度计算可以使用以下公式进行：\[w_k = k \times \frac{f_s}{f_y} \times \frac{M_s}{b \times d}\]其中，\(w_k\)为裂缝宽度，\(k\)为调整系数，\(f_s\)为梁内应力，\(f_y\)为钢筋的屈服强度，\(M_s\)为抗弯强度矩，\(b\)为截面宽度，\(d\)为截面有效高度。

2.裂缝宽度计算包含的因素在裂缝宽度计算中，需要考虑梁内应力、钢筋的屈服强度以及抗弯强度矩等因素。

通过对这些因素的综合考虑，可以准确计算出钢筋混凝土受弯构件的裂缝宽度，从而确保结构的安全性。

三、挠度计算1.挠度计算公式钢筋混凝土受弯构件的挠度计算可以使用以下公式进行：\[f = \frac{5 \times q \times l^4}{384 \times E \times I}\]其中，\(f\)为挠度，\(q\)为荷载，\(l\)为构件长度，\(E\)为弹性模量，\(I\)为惯性矩。

2.挠度计算的影响因素在挠度计算中，荷载、构件长度、弹性模量和惯性矩等因素都会对挠度产生影响。

通过对这些因素进行综合考虑，并结合实际工程情况，可以准确计算出钢筋混凝土受弯构件的挠度，从而满足设计要求。

四、个人观点和理解钢筋混凝土受弯构件的裂缝宽度和挠度计算是结构设计中的重要内容，它直接关系到结构的安全性和稳定性。

在实际工程中，我们需要充分理解裂缝宽度和挠度计算的原理和方法，结合设计规范和实际情况，确保结构设计的合理性和可行性。

五、总结与展望通过本文的分析，我们深入探讨了钢筋混凝土受弯构件的裂缝宽度和挠度计算，并对其进行了详细介绍。