近圆轨道遥感卫星星下点轨迹的计算

卫星的近地点和远地点速度公式
1. 卫星运动的基本原理。

- 根据开普勒第二定律，卫星与中心天体的连线在相等的时间内扫过相等的面积。

设卫星在近地点的速度为v_1，近地点到中心天体的距离为r_1；在远地点的速度为v_2，远地点到中心天体的距离为r_2。

- 由于卫星在运动过程中机械能守恒，其机械能E = (1)/(2)mv^2-(GMm)/(r)（其中m为卫星质量，v为卫星速度，r为卫星到中心天体的距离，G为引力常量，M 为中心天体质量）是一个常量。

2. 近地点和远地点速度公式推导。

- 根据开普勒第二定律可得v_1r_1 = v_2r_2，即v_2=(r_1)/(r_2)v_1。

- 由机械能守恒定律E_1 = E_2，(1)/(2)mv_1^2-(GMm)/(r_1)=(1)/(2)mv_2^2-(GMm)/(r_2)。

- 将v_2=(r_1)/(r_2)v_1代入机械能守恒方程(1)/(2)mv_1^2-
(GMm)/(r_1)=(1)/(2)m((r_1)/(r_2)v_1)^2-(GMm)/(r_2)。

- 化简可得v_1=√(frac{2GM r_2){(r_1 + r_2)r_1}}，v_2=√(frac{2GM r_1){(r_1 + r_2)r_2}}。

卫星星下点轨迹计算1. 前言随着卫星技术的不断发展与应用，卫星星下点轨迹计算越来越重要。

卫星星下点轨迹计算可以帮助我们预测卫星通过的起点、终点以及轨迹。

这对于卫星通信、卫星遥感、导航等应用非常有用。

下面，我们会详细介绍卫星星下点轨迹计算的原理和方法。

2. 卫星星下点轨迹计算的原理卫星星下点轨迹计算就是把卫星的轨道经纬度转化为地面的经纬度。

卫星的轨道是一条椭圆，而卫星的星下点（也就是卫星从地面看到的影子）则在地球的球面上。

因此，我们需要用到球面三角形学来求出卫星星下点的经纬度。

球面三角形学是解决球面上三角形的形状和位置的科学。

3. 卫星星下点轨迹计算的方法3.1 坐标系转换首先，我们需要把卫星的赤道坐标系转化为地心惯性坐标系，然后再把地心惯性坐标系转化为地心地固坐标系。

3.2 椭球体转换我们还需要对卫星的轨道进行椭球体转换。

地球是一个略带扁平的椭球体，因此我们需要用到椭球坐标系来描述卫星的位置。

3.3 计算卫星坐标通过把转换后的卫星轨道信息代入文献中的卫星机轨迹计算公式，我们可以得到任意时刻卫星的坐标。

3.4 计算卫星星下点坐标最后一步是计算卫星星下点的经纬度。

这可以通过球面三角形学中的余弦定理来完成。

根据余弦定理，我们可以通过已知的三角形边长（卫星高度、地球半径和卫星天线到卫星向地球的连线的夹角）求出三角形的角度。

利用这些角度，我们可以通过三角函数算出卫星星下点的经纬度。

4. 结论卫星星下点轨迹计算是卫星应用中的重要环节之一，可以帮助我们预测卫星的轨迹和星下点位置。

这对于卫星通信、卫星遥感、导航等应用非常重要。

通过本文的介绍，我们希望读者能够了解卫星星下点轨迹计算的原理和方法，从而更好地理解卫星应用中的相关内容。

卫星星下点轨迹计算
卫星星下点轨迹计算是指通过卫星的轨道参数和地球的形状参数，计算出卫星在地球上的投影点的运动轨迹。

这个过程需要考虑到地球的自转、引力场、大气阻力等因素，因此需要进行复杂的数学模型和计算。

我们需要了解卫星的轨道参数。

卫星的轨道通常由半长轴、偏心率、轨道倾角、升交点赤经和升交点赤纬等参数来描述。

这些参数可以通过卫星的发射信息或者卫星测量数据来获取。

我们需要了解地球的形状参数。

地球并不是一个完美的球体，而是一个略带扁平的椭球体。

因此，我们需要知道地球的赤道半径和极半径，以及地球的引力场参数。

接下来，我们需要考虑地球的自转。

地球的自转会导致卫星在地球上的投影点产生运动，因此我们需要考虑地球自转的角速度和卫星的轨道倾角。

我们需要考虑大气阻力对卫星的影响。

大气阻力会导致卫星的轨道逐渐下降，因此我们需要考虑大气密度和卫星的速度等因素。

通过以上的参数和因素，我们可以建立一个复杂的数学模型来计算卫星星下点轨迹。

这个模型需要考虑到各种因素的相互作用，因此需要进行大量的计算和模拟。

同时，由于地球和卫星的运动都是三
维的，因此我们需要进行三维的计算和可视化。

卫星星下点轨迹计算在卫星导航、遥感、气象等领域都有着广泛的应用。

通过计算卫星星下点轨迹，我们可以更加准确地预测卫星的位置和运动轨迹，从而提高卫星的使用效率和精度。

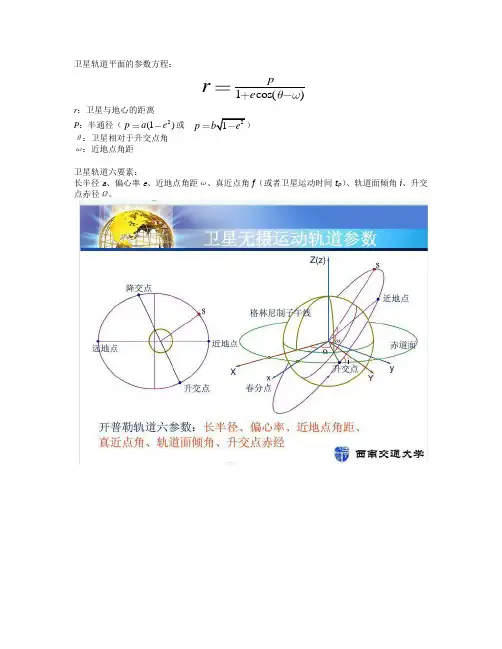
卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。

OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。

两个坐标系：地心轨道坐标系、赤道惯性坐标系。

地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。

赤道惯性坐标系：OXYZ,X轴指向春分点。

由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。

在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。

1）计算平均角速度n
已知卫星轨道长半轴a，利用计算平均角速度。

2）计算平近点角M和偏近点角E
已知卫星过近地点时刻τ和卫星轨道离心率e，利用平近点交M和时间t的关系式计算平近点角M。

利用开普勒方程计算偏近点角E。

3）计算卫星向径的模r
利用式计算。

4）计算卫星真近点角f
利用计算。

5）计算卫星在轨道平面直角坐标系中的坐标（x’,y’）
利用式计算，其中r已计算出，如下
注意此处可以通过偏近点角E和椭圆参数直接计算坐标。

6）卫星在天球坐标系中的位置
由轨道倾角i，升交点赤经Ω和近升角距ω三个轨道参数，可以计算出卫星在天球坐标系中的位置。

此处R下标1、2、3对应的为x’、y’、z’的坐标轴，负号表示顺时针旋转。

7）卫星在瞬时地球坐标系中的位置
上面所求的坐标或速度，一般为惯性坐标系J2000.0。

要实现天球坐标系到地球坐标系的转换，应该首先考虑岁差和章动的影响先转换到瞬时真天球坐标系中。

但在实际应用中，如GPS导航电文的轨道根数提供的轨道根数，所求的上述结果已对应于瞬时天球坐标系，因而只需进行Z轴旋转GAST(t)，就转换到瞬时地球坐标系。

8）卫星在协议地球坐标系中的位置
若考虑极移的影响，有
以上就完成了卫星位置的计算。

一、实验名称遥感卫星近地圆轨道设计及仿真二、实验要求设计一个卫星用途为遥感卫星，要求卫星对福建省福州地区进行全天候观测，轨道选用低轨圆轨道，1天内至少要经过福州上空6次，轨道高度为272km，要求卫星模型具有合适大小。

三、实验步骤1、双击桌面上的STK9图标，启动软件在弹出的warning窗口中，单击Continue Startup按钮，然后新建场景，单击Create a New Scenario；2、在弹出的窗口中修改场景的名称name，同时设置仿真分析的起始时间为1 Jul 2007 12:00:00.000 UTCG和终止时间2 Jul 2007 12:00:00.000 UTCG，设置完成后点击ok按钮，然后我们即可在Object Browser （对象浏览器）中看到新建的场景Scenario1，如果自动跳出一个叫做“Insert STK Objects”的窗口；3、在场景中填加卫星：在“Insert STK Objects”窗口的Scenario Objects下单击Satellite 图标，然后在右方的Select A Method下单击选中Insert Default图标，单击“Insert…”按钮，在“Object Browser”窗口添加了Satellite1图标，生成一颗卫星。

4、在卫星上填加敏感器：继续在“Insert STK Objects”窗口的Attached Objects下单击Sensor图标，然后在右方的Select A Method下单击选中Insert Default图标，单击“Insert…”按钮。

此时会弹出“Select Object”窗口，单击“OK”按钮，在在“Object Browser”窗口添加了Sensor1图标。

5、在场景中填加目标城市福州：继续在“Insert STK Objects”窗口的Scenario Objects 下单击Target图标，然后在右方的Select A Method下单击选中Select From City Database图标，单击“Insert…”按钮，会弹“Insert From City Database”窗口。

GPS卫星轨道的理论和计算1.引言GPS全球定位系统是一种利用卫星定位技术实现精确定位和时间同步的全球导航卫星系统，由美国的军方开发，目前已经向全世界开放。

其中，GPS卫星是实现GPS定位的核心部分，而卫星的轨道是卫星运动的基础，也是GPS定位的重要参考基准。

2. GPS卫星轨道的理论GPS卫星运动的物理过程与地球引力和旋转的运动规律密切相关。

GPS卫星的轨道通常是圆形或近似圆形的，但在现实世界中，卫星的轨道呈现为稍微不规则的椭圆形。

GPS卫星成功运行的关键在于，卫星轨道的参数设定和运行稳定性的维持，这些问题都需要靠严密的理论计算处理。

2.1 GPS卫星轨道的类型GPS卫星轨道主要分为两类：中心天球和地球中心。

中心天球轨道不考虑地球的自转和引力等因素，只以恒星为参照物，将GPS卫星的轨道作为一个运行的天体，根据行星运动学的定义和理论计算出卫星的运行轨迹。

而地球中心轨道则更加复杂，它不仅需要考虑恒星引力，还要包括地球引力、地球自转引起的离心效应等因素，这些因素对于卫星的轨迹有着较大的影响。

2.2 GPS卫星轨道计算方法GPS卫星轨道的计算方法比较复杂，需要使用天文学和航空航天学等多个领域的相关知识。

目前，根据GPS卫星运行的特点，卫星轨道的计算主要分为以下两种方法。

2.2.1 斯塔克-德鲁瑟方法斯塔克-德鲁瑟方法也称为SDP4算法，它是一种常用的GPS卫星轨道计算方法。

该方法通过外推算法预测卫星位置，并在每个预报周期内根据实际观测数据进行校正。

SDP4方法的优点是速度快，精度较高，但在某些情况下可能会出现误差。

2.2.2 数值积分方法数值积分方法是一种更加精确的GPS卫星轨道计算方法，它可以模拟卫星运动在地球引力和自转等因素的影响下的完整轨迹。

该方法的优点在于精确度很高，但计算量较大，需要进行多次迭代计算。

3. GPS卫星轨道计算案例以GPS卫星PRN25为例，我们来看看如何进行轨道计算。

3.1 基本信息卫星编号：PRN25发射时间：1987年6月10日升轨期：20分钟轨道高度：20200公里3.2 计算过程我们可以通过卫星计算软件，填入卫星的基本信息，以及需要预测的时间和卫星位置，进行轨道计算。

卫星近地点远地点速度计算一、卫星近地点远地点速度计算相关知识卫星在近地点和远地点的速度计算可是个很有趣的话题呢！咱们先得知道一些基本的原理。

卫星绕着地球转的时候，它的运动是受到万有引力的影响的。

在近地点，卫星离地球比较近，这时候它的速度相对比较快。

为什么呢？就好像你在一个圆形跑道的内侧跑步，你得跑快一点才能维持在这个轨道上。

根据万有引力公式 F = GMm/r²（这里G是引力常量，M是地球质量，m是卫星质量，r是卫星到地球中心的距离），再结合向心力公式 F = mv²/r，我们可以推导出卫星速度的计算公式。

在近地点，r比较小，为了平衡万有引力，v就会比较大。

而在远地点呢，卫星离地球远一些，r变大了。

按照前面的公式，这时候卫星的速度就会相对小一些。

二、具体计算示例咱们假设一颗卫星，地球质量M = 5.97237×10²⁴kg，引力常量G = 6.67430×10⁻¹¹N·m²/kg²。

如果卫星在近地点的高度是h₁ = 200km（这里我们要把这个高度加上地球半径R = 6371km得到卫星到地球中心的距离r₁），那r₁ = 6371 + 200 = 6571km = 6571000m。

我们把数值代入公式v₁ = √(GM/r₁)，就可以算出近地点的速度啦。

v₁= √((6.67430×10⁻¹¹×5.97237×10²⁴)/6571000) ≈ 7786m/s。

要是卫星在远地点的高度h₂ = 1000km，那r₂ = 6371+1000 = 7371km = 7371000m。

再代入公式v₂ = √(GM/r₂)，算出远地点速度。

v₂= √((6.67430×10⁻¹¹×5.97237×10²⁴)/7371000) ≈ 7350m/s。

1）计算平均角速度n已知卫星轨道长半轴a ，利用23n a μ=计算平均角速度。

2）计算平近点角M 和偏近点角E已知卫星过近地点时刻τ和卫星轨道离心率e ，利用平近点交M 和时间t 的关系式()M n t τ=-计算平近点角M 。

利用开普勒方程sin E M e E =+计算偏近点角E 。

3）计算卫星向径的模r利用式(1cos )r a e E =-计算。

4）计算卫星真近点角f 利用2(1)1cos 1cos a e P r e f e f-==--计算。

21(1)cos 1/a e f e r -⎡⎤⎛⎫-=-⎢⎥ ⎪⎝⎭⎣⎦5）计算卫星在轨道平面直角坐标系中的坐标（x ’,y’）利用式cos (cosE )sin sin (1cosE)x r y r f a e f b E E r a e =⎫⎪⎪=⎬⎪=⎪⎭⋅=-⋅===-计算，其中r 已计算出，如下''cos (cosE )sin sin x r y r f a e f b E E =⎫⎪⎬=⎪⎭⋅=-⋅== 注意此处可以通过偏近点角E 和椭圆参数直接计算坐标。

6）卫星在天球坐标系中的位置由轨道倾角i ，升交点赤经Ω和近升角距ω三个轨道参数，可以计算出卫星在天球坐标系中的位置。

()()313,,()()()',','T T x y z R R i R x y z ω=-Ω--此处R 下标1、2、3对应的为x ’、y’、z’的坐标轴，负号表示顺时针旋转。

7）卫星在瞬时地球坐标系中的位置上面所求的坐标或速度，一般为惯性坐标系J2000.0。

要实现天球坐标系到地球坐标系的转换，应该首先考虑岁差和章动的影响先转换到瞬时真天球坐标系中。

但在实际应用中，如GPS 导航电文的轨道根数提供的轨道根数，所求的上述结果已对应于瞬时天球坐标系，因而只需进行Z 轴旋转GAST(t)，就转换到瞬时地球坐标系。

()[]()3X,,GAST(t),,T T Y Z R x y z = (0.1)8）卫星在协议地球坐标系中的位置若考虑极移的影响，有()()21X,,(x )(y )X,,T T p p CTS Y Z R R Y Z =-- (0.2) 以上就完成了卫星位置的计算。

近圆轨道遥感卫星星下点轨迹的计算
近圆轨道遥感卫星星下点轨迹的计算是将近圆轨道的参数，即空
间方位角、入射角与距离在历元上收集的遥感数据及相应时间戳元素
之间建立联系的一类数学计算问题。

使用近圆轨道遥感卫星的星下点计算，首先需要根据天文学理论，确定卫星初始状态，即相对于地心惯性系的位置、速度以及参考时间。

其次，根据牛顿动力学模型，计算出各历元时刻的位置和速度，包括
地心高度h, 地心位置x，地心位置y，地心位置z，地心速度u，地心
速度v，地心速度w。

接着，可以利用投影变换，计算出每时标的空间
方位角、入射角和距离，并将此参数投影到地表，最后得到一组精准
的空间相对位置坐标。

还有一种计算方法是利用定矩和轨道椭球体法，利用定矩部分可
以通过初始状态，以及地心高度、时间，计算出太阳系内每一个时标
下卫星的相对位置，再利用椭球体法，将卫星位置转换成地心坐标，
最后由地心坐标可以计算出空间方位角、入射角和距离，并有精确的
坐标值。

因此，在近圆轨道遥感卫星星下点轨迹的计算中，采用牛顿动力
学模型和定矩及轨道椭球体法是一种高精度的计算方式，需要精准的
参数，它们可以提供准确可靠的空间相对位置坐标。

近圆轨道遥感卫星星下点轨迹的计算
近圆轨道遥感卫星星下点轨迹的计算是一项关于近圆轨道遥感卫星图像采集规律性的研究技术，它可以提供有效的图像数据，以满足用户对卫星信息数据产品的需求。

经过多年的研究，已经提出了计算近圆轨道遥感卫星星下点轨迹的全部流程，包括轨道动态学的建立，解析法的原理及其相关算法，现代卫星运动学及其应用，星下点轨迹计算步骤及算法等……
首先，近圆轨道遥感卫星的星下点轨迹计算，需要先建立轨道动态学，形成轨道参考系下的三维空间几何轨道动态模型。

该模型将会考虑到卫星各种外力、温度等因素对轨道运行的影响，从而决定卫星的立体运动状态。

其次，接着就要采用解析法的原理，如径向-轨向方程法，通过解决解析方程，来提取给定时刻的轨道参数的值，从而计算给定时刻的星下点轨迹。

其次，考虑到现代卫星运动学真实性，一般情况下，用现代卫星运动学及其应用微弱响应理论（GWRT）或理论微弱响应特征（RTC）来分析星下点轨迹，可以使其遥感应用变得更加准确。

最后，采用高精度计算软件，实施星下点轨迹计算，如采用Ephemeris及其它星轨数据等。

这些软件可以实现卫星状态向量的迭代计算，从而精确算出卫星的星下点轨迹。

总之，计算近圆轨道遥感卫星星下点轨迹，需要建立轨道动态学模型，采用解析法原理，现代卫星运动学及其应用以及低姿态卫星运动学计算等一系列精密的算法才能够得出准确的结果。

近圆轨道遥感卫星星下点轨迹的计算
张云彬;张永生
【期刊名称】《测绘科学技术学报》
【年(卷),期】2001(018)004
【摘要】根据遥感卫星轨道的特点,提出了计算近圆轨道卫星星下点轨迹的算法,并对其进行了精度评估.结果表明这种算法是快捷和有效的,能够满足卫星规划阶段对轨道精度的要求.
【总页数】3页(P257-259)
【作者】张云彬;张永生
【作者单位】信息工程大学测绘学院,;信息工程大学测绘学院,
【正文语种】中文
【中图分类】P228
【相关文献】
1.J2摄动下脉冲推力星下点轨迹调整解析算法 [J], 盛靖;张刚;耿云海
2.一类由星下点反算卫星近圆回归轨道的方法 [J], 段方;刘建业
3.近圆低轨道控制量简易计算方法 [J], 李英良;林西强;谭炜;李革非
4.星下点轨迹有限范围照相目标的快速计算 [J], 陈金勇;彭会湘;张学庆
5.星下点轨迹为"∞"字形同步卫星轨道的实现及应用 [J], 李红;包海涛
因版权原因，仅展示原文概要，查看原文内容请购买。