卫星轨道计算.doc

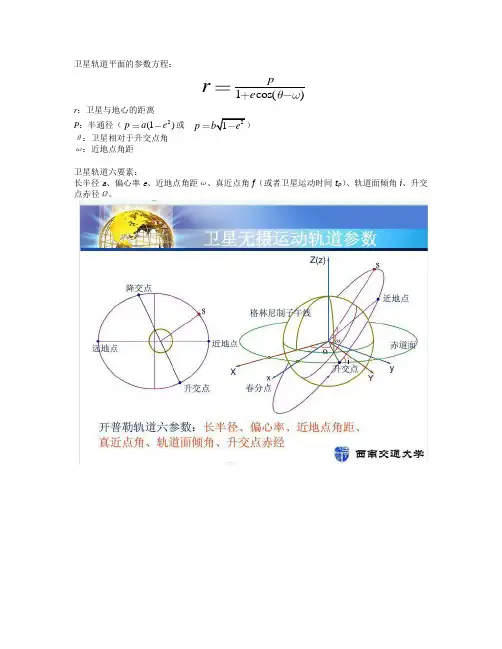
卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。

OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。

两个坐标系：地心轨道坐标系、赤道惯性坐标系。

地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。

赤道惯性坐标系：OXYZ,X轴指向春分点。

由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。

在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。

卫星轨道参数详解⽬录⼀.卫星根数1.1 六根数1.2 卫星星历两⾏根数（TLE(two line element)）tle1:tle2:1.3 航天器的运⾏轨道分类1.4轨道速度的计算⼀.卫星根数1.1 六根数⼈造卫星轨道六要素（也称为轨道六根数）是⽤于表征卫星轨道形状、位置及运动等属性的参数，可⽤来确定任意时刻卫星的轨道和位置。

通常的轨道六根数指的是：半长轴a、离⼼率e、轨道倾⾓i、近⼼点辐⾓ω、升交点经度Ω和真近点⾓φ。

六根数中，前2项确定了轨道形状，第3、4、5项确定了轨道平⾯所处的位置，第6项确定了卫星在轨道中当前所处位置（注意：第6项除了⽤真近点⾓来表征外，还常常⽤平近点⾓、过升交点时刻、过近地点时刻等参量表征，其效果是等价的。

六根数⽰意图半长轴a:这个根数决定了卫星轨道形成的椭圆长半轴的长度，及轨道的⼤⼩。

同时，这个根数也决定了发射卫星到这个轨道需要多少能量，因为根据活⼒公式，⼀个确定轨道的机械能是固定的。

不同任务类型的卫星，或者运载约束，⼯作在不同的轨道⾼度上。

发射到不同轨道所需要的能量都需要依靠半长轴来计算。

如下图所⽰，飞得越⾼的卫星速度越慢，也是依据半长轴计算⽽来的。

偏⼼率e:跟椭圆的扁率是⼀个意思，代表轨道偏⼼的程度。

偏⼼率近似等于0的轨道⼀般称为近圆轨道，此时地球的质⼼⼏乎与轨道⼏何中⼼重合。

偏⼼⼤于0⼩于1，轨道就呈椭圆状，偏⼼率越⼤轨道越扁。

轨道倾⾓i:即轨道平⾯与⾚道平⾯之间的夹⾓，⽤于描述轨道的倾斜程度，简单地说就是轨道平⾯相对于地球⾚道平⾯是躺着的还是⽴着的或者是斜着的。

卫星轨道的倾⾓决定了卫星星下点所能覆盖的地理⾼度，并对发射场和运载⽕箭的运⼒形成硬性约束。

具体⽽⾔，若想卫星⾏下点轨迹覆盖⾼纬度地区，则卫星轨道倾⾓不能⼩于该纬度；发射场的纬度不能⾼于卫星轨道倾⾓；在半长轴和发射场相同的情况下，运载⽕箭发射倾⾓更⾼的卫星需要提供更多的能量。

升交点⾚经Ω：理解这个轨道根数需要在称为惯性系的三维空间中进⾏。

卫星运动椭圆轨道计算
卫星的运动轨迹可以使用椭圆轨道来描述。

在计算椭圆轨道时，需要考虑卫星的速度、质量、引力、离心力等因素。

下面将详细介绍卫星运动椭圆轨道计算的相关知识。

首先，我们需要了解椭圆轨道的基本定义。

椭圆轨道是指一个物体以一个焦点为中心，另一个焦点为另一端点的椭圆运动轨迹。

在卫星运动中，这两个焦点分别是地球的中心和一个虚拟点。

其次，我们需要了解椭圆轨道的参数。

椭圆轨道的参数包括长轴、短轴、偏心率、倾角等。

其中，长轴是椭圆轨道的最长直径，短轴是椭圆轨道的最短直径，偏心率是椭圆轨道焦点距离轨道中心的距离与长轴的比值，倾角是轨道平面与地球赤道面的夹角。

接下来，我们需要了解卫星的运动方程。

在计算卫星的运动轨迹时，需要根据牛顿运动定律来求解卫星的加速度和速度，然后再根据运动方程求解卫星的位置。

具体来说，卫星的运动方程为：
f(r) = r - (a*(1 - e^2)/(1 - e*cos(theta))) - r0 = 0
其中，f(r)是卫星的运动方程，r是卫星距离地心的距离，a是椭圆轨道的长轴，
e是椭圆轨道的偏心率，theta是卫星当前的真近点角度，r0是卫星当前的距离地心的距离。

最后，我们需要了解卫星轨道的计算方法。

在计算卫星轨道时，可以采用数值模拟和解析计算两种方法。

数值模拟方法利用计算机模拟卫星在轨道上的运动，可以得到较为准确的结果；解析计算方法则通过求解卫星的运动方程来计算卫星的运动轨迹，可以得到精确的结果，但需要较高的数学能力。

以上是关于卫星运动椭圆轨道计算的相关知识介绍，希望对您有所帮助。

卫星轨道计算1.轨道根数如果知道卫星的轨道根数，可以根据它们求出卫星在任一时刻的位置。

1．1 开普勒六参数卫星的轨道根数包括六个积分常数，如图1，包括，a为轨道长半轴；e为轨道偏心率；i 为卫星运动轨道面与赤道面的夹角；Ω为卫星轨道升交点N的赤道经度(自春分点算起)；ω为轨道近地点极角，即轨道平面内升交点到近地点的角度；ζ为卫星过近地点时刻1. 轨道半长轴，是椭圆长轴的一半。

2. 轨道偏心率，也就是椭圆两焦点的距离和长轴比值。

3. 轨道倾角，这个是轨道平面和地球赤道平面的夹角。

对于位于赤道上空的同步静止卫星来说，倾角就是0。

4. 升交点赤经：卫星从南半球运行到北半球时穿过赤道的那一点叫升交点。

这个点和春分点对于地心的张角称为升交点赤经。

5. 近地点幅角：这是近地点和升交点对地心的张角。

6. 过近地点时刻：卫星位置随时间的变化需要一个初值。

其中i、Ω、ω决定卫星轨道平面和长轴在空间的位置，而a、e、ζ可求出卫星在任何时刻在轨道上的位置。

1．2 TLE卫星星历TLE两行根数格式如下：AAAAAAAAAAAAAAAAAAAAAAAA1 NNNNNU NNNNNAAA NNNNN.NNNNNNNN +.NNNNNNNN +NNNNN-N +NNNNN-N N NNNNN2 NNNNN NNN.NNNN NNN.NNNN NNNNNNN NNN.NNNN NNN.NNNN NN.NNNNNNNNNNNNNN以国际空间站为例ISS (ZARYA)1 25544U 98067A 06052.34767361.00013949 00000-0 97127-4 0 39342 25544 051.6421 063.2734 0007415 308.6263 249.9177 15.74668600414901（1）第0行第0行是一个最长为24个字符的卫星通用名称，由卫星所在国籍的卫星公司命名，如SINOSAT 3。

卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。

OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。

两个坐标系：地心轨道坐标系、赤道惯性坐标系。

地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。

赤道惯性坐标系：OXYZ,X轴指向春分点。

由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。

在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。

一．GPS观测量接收机在观测相位和伪距数据的同时，还将广播星历和预报星历记录下来。

接收GPS信号还能获取纳秒级精度的时间基准信号。

由于接收机的型号很多，厂商设计的数据格式各不相同，国际上为了能统一使用不同接收机的数据，设计了一种与接收机无关的RINEX(The Receiver Independent Exchange Format)格式，目前已使用2号版本。

下面分别介绍RINEX 2格式的广播星历文件、观测数据文件、和地面气象数据文件。

RINEX 2格式的GPS数据文件的命名规则为：.s s s s d d d f y y t其中：ssss～以4个字节表示的台站名；ddd～文件中第一组数据观测时间的年积日(例如：1月1日为001，2月2日为032)；f～该站该日收到的某类文件的顺序号，0表示只有一个；yy～以两位数表示的年(例如：96表示1996年)；t～文件种类：O～观测数据文件；N～广播星历文件；M～地面气象数据文件。

为了便于交流，RINEX 2格式的GPS数据文件均以①无带标；②ASCII码；③每个记录长度为80个字符，块大小为8000；录制在磁带上，磁带上的第一个文件是全部文件的目录。

但目前国际上的IGS等组织是通过通讯方式(Internet网)，来快速地提取全球GPS长年观测站数据的，并将数据存在大型计算机中，使用着可通过Internet网任意提取。

应注意，在RINEX 2格式的GPS数据中，时间均以GPST计，即与UTC要差一个整数跳秒数。

⒈广播星历文件接收机锁定卫星并解出C/A码后，就能取得广播星历，即卫星坐标计算参数，在实时GPS应用中，它是必不可少的，大部分的工程网观测数据的后处理也采用广播星历。

RINEX 2格式的广播星历文件如下表2.1.1所示，作为例子，表中给出了PRN9和PRN17两颗卫星的广播星历数据，PRN表示GPS卫星的伪随机编号号码，GPS卫星在有些场合采用美国航空与航天局NASA(National Aeronautics and Space Administration)的编号。

1）计算平均角速度n
已知卫星轨道长半轴a，利用计算平均角速度。

2）计算平近点角M和偏近点角E
已知卫星过近地点时刻τ和卫星轨道离心率e，利用平近点交M和时间t的关系式计算平近点角M。

利用开普勒方程计算偏近点角E。

3）计算卫星向径的模r
利用式计算。

4）计算卫星真近点角f
利用计算。

5）计算卫星在轨道平面直角坐标系中的坐标（x’,y’）
利用式计算，其中r已计算出，如下
注意此处可以通过偏近点角E和椭圆参数直接计算坐标。

6）卫星在天球坐标系中的位置
由轨道倾角i，升交点赤经Ω和近升角距ω三个轨道参数，可以计算出卫星在天球坐标系中的位置。

此处R下标1、2、3对应的为x’、y’、z’的坐标轴，负号表示顺时针旋转。

7）卫星在瞬时地球坐标系中的位置
上面所求的坐标或速度，一般为惯性坐标系J2000.0。

要实现天球坐标系到地球坐标系的转换，应该首先考虑岁差和章动的影响先转换到瞬时真天球坐标系中。

但在实际应用中，如GPS导航电文的轨道根数提供的轨道根数，所求的上述结果已对应于瞬时天球坐标系，因而只需进行Z轴旋转GAST(t)，就转换到瞬时地球坐标系。

8）卫星在协议地球坐标系中的位置
若考虑极移的影响，有
以上就完成了卫星位置的计算。

卫星轨道动⼒学数值计算⽬录1星历计算的时间和坐标系统 (2)1.1 有关的时间系统与坐标系统 (2)1.1.1 时间系统及其换算 (2)1.1.2 坐标系统及其换算 (4)1.2 计算单位和有关常数 (7)2 轨道动⼒学计算的基本数学模型 (12)2.1 ⼆体问题 (12)2.2 地球⾮球形引⼒摄动 (12)2.3 ⽇、⽉摄动 (15)2.4 太阳直接辐射压摄动 (16)2.5 地球固体潮摄动 (19)2.6 ⼤⽓阻⼒摄动 (19)2.7 Y轴偏差加速度摄动 (20)2.8 巡航姿态控制动⼒摄动 (20)2.9 其它摄动影响 (21)附录：⽇⽉位置计算 (21)3 轨道计算⽅法 (24)3.1 Runge_Kutta积分法 (24)3.2 Adams_Cowell积分 (25)3.3 轨道计算 (27)3.4 星历的快速插值 (28)4 轨道根数与位置⽮量、速度⽮量的关系 (32)4.1 由位置⽮量和速度⽮量计算轨道根数 (32)4.2 由轨道根数计算位置⽮量和速度⽮量 (33)1星历计算的时间和坐标系统1.1 有关的时间系统与坐标系统轨道计算过程重要涉及到不同的时间系统和坐标系统，下⾯将空间战场环境系统中所涉及到的时间系统和坐标系统进⾏定义，并说明各系统之间的相互关系。

⼀般情况下，仿真系统采⽤的是TDT 时间系统和J2000地⼼惯性坐标系。

1.1.1 时间系统及其换算在轨道计算中，时间是独⽴变量。

但是，在计算不同的物理量时，却使⽤不同的时间系统。

例如：在计算恒星时⽤世界时UT1；定位解算时采⽤GPS 时GPST ；岁差和章动量的计算采⽤TDB 时等。

所以必须清楚各时间系统的定义和各时间系统之间的转换，下⾯给出各种时间系统的定义及它们之间的转换公式。

格林尼治恒星时格林尼治恒星时为春分点对格林尼治平天⽂⼦午⾯的时⾓。

由于岁差、章动原因，它由格林尼治真恒星时（GAST ）和平恒星时（GMST ）之分。

一．GPS观测量接收机在观测相位和伪距数据的同时，还将广播星历和预报星历记录下来。

接收GPS信号还能获取纳秒级精度的时间基准信号。

由于接收机的型号很多，厂商设计的数据格式各不相同，国际上为了能统一使用不同接收机的数据，设计了一种与接收机无关的RINEX(The Receiver Independent Exchange Format)格式，目前已使用2号版本。

下面分别介绍RINEX 2格式的广播星历文件、观测数据文件、和地面气象数据文件。

RINEX 2格式的GPS数据文件的命名规则为：.s s s s d d d f y y t其中：ssss～以4个字节表示的台站名；ddd～文件中第一组数据观测时间的年积日(例如：1月1日为001，2月2日为032)；f～该站该日收到的某类文件的顺序号，0表示只有一个；yy～以两位数表示的年(例如：96表示1996年)；t～文件种类：O～观测数据文件；N～广播星历文件；M～地面气象数据文件。

为了便于交流，RINEX 2格式的GPS数据文件均以①无带标；②ASCII码；③每个记录长度为80个字符，块大小为8000；录制在磁带上，磁带上的第一个文件是全部文件的目录。

但目前国际上的IGS等组织是通过通讯方式(Internet网)，来快速地提取全球GPS长年观测站数据的，并将数据存在大型计算机中，使用着可通过Internet网任意提取。

应注意，在RINEX 2格式的GPS数据中，时间均以GPST计，即与UTC要差一个整数跳秒数。

⒈广播星历文件接收机锁定卫星并解出C/A码后，就能取得广播星历，即卫星坐标计算参数，在实时GPS应用中，它是必不可少的，大部分的工程网观测数据的后处理也采用广播星历。

RINEX 2格式的广播星历文件如下表2.1.1所示，作为例子，表中给出了PRN9和PRN17两颗卫星的广播星历数据，PRN表示GPS卫星的伪随机编号号码，GPS卫星在有些场合采用美国航空与航天局NASA(National Aeronautics and Space Administration)的编号。

卫星轨道动力学数值计算
1.轨道参数：卫星轨道计算需要确定卫星的轨道参数，如半长轴，轨道倾角，近地点角，升交点赤经等。

这些参数必须根据历元计算出来，以确定卫星在指定历元的轨道位置。

2.运动方程：对于卫星的运动，除了已知的轨道参数外，还需要建立一个基本的运动方程，用来描述卫星的运动。

3.动力学模型：动力学模型是用来描述卫星在太空中的运动方程的，可以根据引力加速度来建立运动方程，通过改变模型来模拟不同的太空环境。

4.时间序列：卫星轨道动力学数值计算时，还需要指定一定的时间序列，用来记录卫星在每个时刻的轨道位置，以及卫星在一段时间内的运动过程。

5.计算系统：所有这些参数和模型都需要一个程序来实现，该程序由运算程序和辅助程序组成，根据输入的轨道参数及时间序列，建立动力学模型，计算出卫星在指定时间内的轨道位置。

本文介绍了卫星轨道动力学数值计算方法的基本原理。