数据采样插补

插补的基本概念脉冲增量插补与数据采样插补的特点和区别逐点比较法的基本原理直线插补和圆弧插补
脉冲增量插补和数据采样插补是实现插补的两种不同方法。

脉冲增量插补是将连续的运动轨迹离散化，以一定的脉冲数来表示，通过控制脉冲信号的频率和方向来控制机床的运动方向和速度。

而数据采样插补则是将预先生成的轨迹数据存储在内存中，通过对数据进行采样来得到机床的控制指令。

脉冲增量插补的特点是运算简单，系统响应速度较快，适合于高速运动控制；但由于其离散化的特点，可能会引入累积误差。

数据采样插补的特点是能够精确控制机床的运动轨迹，减小累积误差，但需要占用较大的内存空间。

逐点比较法是一种用于校正控制系统误差的方法。

其基本原理是通过对实际运动轨迹数据和预期轨迹数据进行逐点比较，根据比较结果来调整机床的控制指令，使实际运动轨迹尽可能地与预期轨迹一致。

逐点比较法的关键是选择合适的比较误差补偿算法，以实现高效准确的校正。

直线插补是指在机床坐标系下，按照直线轨迹进行插补运动。

直线插补的计算相对简单，只需要对坐标进行线性插值即可。

圆弧插补是指在机床坐标系下，按照圆弧轨迹进行插补运动。

圆弧插补的计算相对复杂，需要考虑起点、终点和半径等参数，通过数学运算得出插补指令。

总之，插补是机床运动控制的基础，脉冲增量插补和数据采样插补是两种常见的实现方式，逐点比较法是一种用于校正误差的方法，直线插补和圆弧插补则是两种常见的插补方式。

数据采样插补一、概述数据采样插补多用于进给速度要求较高的闭环掌握系统。

它与前面我们介绍的插补方法的最大不同就是前者计算机一般不包含在伺服掌握环内，计算机插补的结果是输出进给脉冲，伺服系统依据进给脉冲进给。

每进给一步（一个脉冲当量），计算机都要进行一次插补运算。

进给速度受计算机插补速度的限制，很难满意现代数控机床高速度的要求。

而后者计算机一般包含在伺服掌握环内。

数据采样插补用小段直线来靠近给定轨迹，插补输出的是下一个插补周期内各轴要运动的距离，不需要每走一个脉冲当量就插补一次，可达到很高的进给速度。

1. 数据采样插补的基本原理粗插补：采纳时间分割思想，依据进给速度F和插补周期T，将廓型曲线分割成一段段的轮廓步长L，L=FT，然后计算出每个插补周期的坐标增量。

精插补：依据位置反馈采样周期的大小，由伺服系统的硬件完成。

2. 插补周期和检测采样周期插补周期大于插补运算时间与完成其它实时任务时间之和，现代数控系统一般为2~4ms，有的已达到零点几毫秒。

插补周期应是位置反馈检测采样周期的整数倍。

3.插补精度分析直线插补时，轮廓步长L与被加工直线重合，没有插补误差。

圆弧插补时，轮廓步长L作为弦线或割线对圆弧进行靠近，存在半径误差。

二、数据采样法直线插补1.插补计算过程（1）插补预备主要是计算轮廓步长l＝FT及其相应的坐标增量。

（2）插补计算实时计算出各插补周期中的插补点（动点）坐标值。

2.有用的插补算法（1）直线函数法插补预备：插补计算：2）进给速率数法（扩展DDA法）插补预备: 引入步长系数K则插补计算：三、数据采样法圆弧插补1. 直线函数法（弦线法）如图5-13所示，要加工圆心在原点O（0，0）、半径为R的第一象限顺圆弧，在顺圆弧上的B点是继A点之后的插补瞬时点，两点的坐标分别为A（Xi，Yi）、B（Xi＋1，Yi＋1），现求在一个插补周期T内X 轴和Y轴的进给量△X、△Y。

图中的弦AB是圆弧插补时每个插补周期内的进给步长l，AP是A点的圆弧切线，M是弦的中点。

数控加工中两种插补原理及对应算法数控机床上进行加工的各种工件，大部分由直线和圆弧构成。

因此，大多数数控装置都具有直线和圆弧的插补功能。

对于非圆弧曲线轮廓轨迹，可以用微小的直线段或圆弧段来拟合。

插补的任务就是要按照进给速度的要求，在轮廓起点和终点之间计算出若干中间控制点的坐标值。

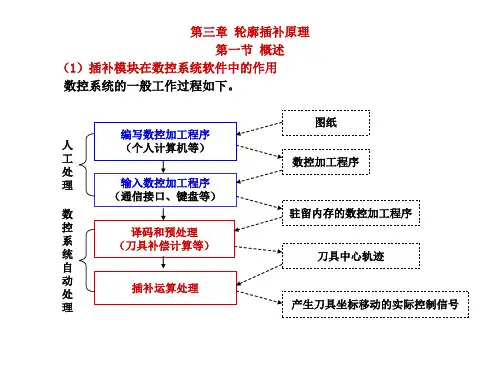
由于每个中间点计算的时间直接影响数控装置的控制速度，而插补中间点的计算精度又影响整个数控系统的精度，所以插补算法对整个数控系统的性能至关重要，也就是说数控装置控制软件的核心是插补。

插补的方法和原理很多，根据数控系统输出到伺服驱动装置的信号的不同，插补方法可归纳为脉冲增量插补和数据采样插补两种类型。

一、脉冲增量插补这类插补算法是以脉冲形式输出，每次插补运算一次，最多给每一轴一个进给脉冲。

把每次插补运算产生的指令脉冲输出到伺服系统，以驱动工作台运动。

一个脉冲产生的进给轴移动量叫脉冲当量，用δ表示。

脉冲当量是脉冲分配计算的基本单位，根据加工的精度选择，普通机床取δ＝0.01mm，较为精密的机床取δ＝1μm或0.1μm。

插补误差不得大于一个脉冲当量。

这种方法控制精度和进给速度低，主要运用于以步进电动机为驱动装置的开环控制系统中。

二、数据采样插补数据采样插补又称时间标量插补或数字增量插补。

这类插补算法的特点是数控装置产生的不是单个脉冲，而是数字量。

插补运算分两步完成。

第一步为粗插补，它是在给定起点和终点的曲线之间插入若干个点，即用若干条微小直线段来拟合给定曲线，每一微小直线段的长度△L都相等，且与给定进给速度有关。

粗插补时每一微小直线段的长度△L与进给速度F和插补T周期有关，即△L＝FT。

数字化实训报告一数据采样差补简介所谓数据采样插补法，或称为时间分割法。

它尤其适合于闭环和半闭环以直流或交流电机为执行机构的位置采样控制系统。

这种方法是把加工一段直线或圆弧的整段时间细分为许多相等的时间间隔，称为单位时间间隔（或插补周期）。

每经过一个单位时间间隔就进行一次插补计算，算出在这一时间间隔内各坐标轴的进给量，边计算，边加工，直至加工终点。

与基准脉冲插补法不同，采用数据采样法插补时，在加工某一直线段或圆弧段的加工指令中必须给出加工进给速度F，先通过速度计算，将进给速度分割成单位时间间隔的插补进给量L（或称为轮廓步长），又称为一次插补进给量。

这类算法的核心问题是如何计算各坐标轴的增长数∆x和∆y（而不是单个脉冲），有了前一插补周期末的动点位置值和本次插补周期内的坐标增长段，就很容易计算出本插补周期末的动点命令位置坐标值。

对于直线插补来讲，插补所形成的轮廓步长子线段（即增长段）与给定的直线重合，不会造成轨迹误差。

而在圆弧插补中，因要用切线或弦线来逼近圆弧，因而不可避免地会带来轮廓误差。

其中切线近似具有较大的轮廓误差而不大采用，常用的是弦线逼近法。

有时，数据采样插补是分两步完成的，即粗插补和精插补。

第一步为粗插补，它是在给定起点和终点的曲线之间插入若干个点，即用若干条微小直线段来逼近给定曲线，粗插补在每个插补计算周期中计算一次。

第二步为精插补，它是在粗插补计算出的每一条微小直线段上再做“数据点的密化”工作，这一步相当于对直线的脉冲增量插补。

二直线插补直线插补的情况如右图所示。

要求刀具在XY 平面中作所示的直线运动。

在这一程序段中,每一小段的长度为L=KFT（K进给倍率，F进给速度，T插补周期）。

只要求出∆x和∆y即可。

tanα=X E Y Ecosα=1√1+（tanα）2∆X=L∗cosα∆Y=∆X∗tanα三顺圆圆弧插补3.1公式推导圆弧插补的情况如下。

顺圆弧AB为待加工曲线，可以依据几何知识推导出关系式：∆Y ∆X =X I+0.5∗L∗COSαY I−0.5∗L∗SINα无法求解出∆x和∆y，取α=45°.如此会引起的误差就是下一点可能不在圆弧上面，所以修正关系式为：∆X′=L*COS45X I2+Y I2=(X I+∆X)2+(Y I−∆Y)2AB3.2流程图3.3程序CLOSE&1#1->2500X#2->2500YOPEN PROG 28CLEARINC;增量模式P0=1；每个周期的步长P1=100；半径P2=0；x0P3=100；y0P4=100；x1P5=0；y1P11=0.7071；sin45，cos45P6=SQRT((P4-P2)*(P4-P2)+(P5-P3)*(P5-P3))；始末点距离P7=INT(2*(ASIN(P6/2/P1))*P1/P0)+1；步数WHILE(P7>0)；由步数控制循环P8=ATAN((P2+0.5*P0*P12)/(P3-0.5*P12*P0))；计算新的角度P9=P0*COS(P8)；dxP10=-(P2+0.5*P9)*P9/(P3-0.5*P9)；dyP2=P2+P9；新的x0P3=P3+P10；新的y0X(P9)；电机动作Y(P10)P7=P7-1；步数减一ENDWHILECLOSE四逆圆圆弧插补4.1公式推导圆弧插补的情况如下。

插补方法的分类
1）基准脉冲插补（脉冲增量插补）
每次插补结束时向各运动坐标轴输出一个基准脉冲序列，驱动各坐标轴进给电机的运动。

每个脉冲使坐标轴产生1个脉冲当量的增量，代表刀具或工件的最小位移；脉冲数量代表刀具或工件移动的位移量；脉冲序列频率代表刀具或工件运动的速度。

基准脉冲插补特点：运算简洁，用硬件电路实现，运算速度快。

适用步进电机驱动的、中等精度或中等速度要求的开环数控系统。

有的数控系统将其用于数据采样插补中的精插补。

基准脉冲插补方法：逐点比较法、数字积分法、比较积分法、数字脉冲乘法器法、最小偏差法、矢量判别法、单步追踪法、直接函数法等。

应用较多的是逐点比较法和数字积分法。

2）数据采样插补（数据增量插补、时间分割法）
采纳时间分割思想，依据编程的进给速度将轮廓曲线分割为每个插补周期的进给直线段（又称轮廓步长）进行数据密化，以此来靠近轮廓曲线。

着重解决两个问题——
（1）如何选择插补周期T；
（2）如何计算在一个插补周期内各坐标轴的增量值△x或△y。

闭环、半闭环系统采纳数据采样插补方法。

数据采样插补方法：直线函数法、扩展数字积分法、二阶递归扩展数字积分法、双数字积分插补法等。

在CNC系统中较广泛采用的另一种插补计算方法即所谓数据采样插补法，或称为时间分割法。

它尤其适合于闭环和半闭环以直流或交流电机为执行机构的位置采样控制系统。

这种方法是把加工一段直线或圆弧的整段时间细分为许多相等的时间间隔，称为单位时间间隔（或插补周期）。

每经过一个单位时间间隔就进行一次插补计算，算出在这一时间间隔内各坐标轴的进给量，边计算，边加工，直至加工终点。

与基准脉冲插补法不同，采用数据采样法插补时，在加工某一直线段或圆弧段的加工指令中必须给出加工进给速度v，先通过速度计算，将进给速度分割成单位时间间隔的插补进给量（或称为轮廓步长），又称为一次插补进给量。

例如，在FANUC 7M系统中，取插补周期为8 ms，若v的单位取mm/min，f的单位取mμ/8 ms，则一次插补进给量可用下列数值方程计算：10008260100015vf v⨯⨯==⨯按上式计算出一次插补进给量f后，根据刀具运动轨迹与各坐标轴的几何关系，就可求出各轴在一个插补周期内的插补进给量，按时间间隔（如8 ms）以增量形式给各轴送出一个一个插补增量，通过驱动部分使机床完成预定轨迹的加工。

由上述分析可知，这类算法的核心问题是如何计算各坐标轴的增长数x∆或y∆（而不是单个脉冲），有了前一插补周期末的动点位置值和本次插补周期内的坐标增长段，就很容易计算出本插补周期末的动点命令位置坐标值。

对于直线插补来讲，插补所形成的轮廓步长子线段（即增长段）与给定的直线重合，不会造成轨迹误差。

而在圆弧插补中，因要用切线或弦线来逼近圆弧，因而不可避免地会带来轮廓误差。

其中切线近似具有较大的轮廓误差而不大采用，常用的是弦线逼近法。

有时，数据采样插补是分两步完成的，即粗插补和精插补。

第一步为粗插补，它是在给定起点和终点的曲线之间插入若干个点，即用若干条微小直线段来逼近给定曲线，粗插补在每个插补计算周期中计算一次。

第二步为精插补，它是在粗插补计算出的每一条微小直线段上再做“数据点的密化”工作，这一步相当于对直线的脉冲增量插补。

数据采样插补原理数据采样插补是指在数据分析和处理过程中，由于数据缺失或不完整而需要进行填补的一种方法。

在实际应用中，我们常常会遇到一些数据缺失的情况，例如某些观测点没有数据记录，或者某些时间段没有数据。

这时候，我们就需要使用数据采样插补的方法来填补这些缺失的数据，以便进行后续的分析和处理。

数据采样是指从总体中抽取一部分样本数据进行分析和推断的过程。

在数据采样过程中，我们需要保证样本的代表性和可靠性，以尽可能准确地反映总体的特征。

常用的数据采样方法包括随机抽样、分层抽样、整群抽样等。

通过合理选择采样方法和样本数量，我们可以在一定程度上降低数据采样误差，提高数据分析的准确性和可靠性。

数据插补是指根据已有数据的特征和规律，推断和填充缺失的数据。

数据插补可以通过各种方法进行，常见的方法包括均值插补、中位数插补、回归插补、插值法等。

这些方法都是根据已有数据的特征和规律进行推断和填充，以尽可能准确地恢复缺失的数据。

数据插补的目的是保持数据集的完整性和一致性，使得后续的分析和处理可以顺利进行。

数据采样插补的原理是将数据采样和数据插补两个方法相结合，通过采样得到样本数据，然后根据已有数据的特征和规律进行插补，填补缺失的数据。

这样可以在保持数据集完整性和一致性的同时，尽可能准确地反映总体的特征。

数据采样插补的过程中，我们需要考虑样本的代表性和可靠性，以及插补方法的准确性和可行性，以确保插补结果的准确性和可靠性。

数据采样插补在实际应用中具有广泛的应用场景。

例如，在气象领域，由于观测站点的分布不均匀，某些地区的观测数据可能缺失。

为了分析和预测气象变化，我们需要对这些缺失的数据进行插补，以获得完整的数据集。

又如，在金融领域，由于某些交易记录的缺失或错误，我们需要对这些数据进行插补，以保持数据集的完整性和一致性，以便进行后续的分析和建模。

数据采样插补是一种常用的数据处理方法，它可以在数据缺失或不完整的情况下，通过采样和插补的方法，填补缺失的数据，以保持数据集的完整性和一致性。

#include<stdio.h>#include<math.h>#include<stdlib.h>/********************************************************************/ /* 函数名: InsertPoint *//* 功能：控制机床各轴进给并将进给结果写入文件中 *//* 参数：double x, double y 插补点单位:毫米 *//* 说明：与机床硬件关联，每产生一个点调用一次 *//********************************************************************/ void InsertPoint(double xCur,double yCur){extern FILE *fp;char ch=10;printf("xCur=%f,yCur=%f\n",xCur,yCur);fprintf(fp,"%f,%f",xCur,yCur);fputc(ch,fp);}/********************************************************************/ /* 函数名: Judge_Quadrant *//* 功能：判断参数坐标的所在象限并返回相应象限值 *//* 参数：double x mm *//* double y mm *//********************************************************************/ unsigned short Judge_Quadrant(double x, double y){unsigned short nDir;if (x>=0){ //象限判断if (y>=0){nDir=1;return 1;}else{nDir=4;return 4;}}else{if (y>=0){nDir=2;return 2;}else{nDir=3;return 3;}}}/********************************************************************/ /* 函数名: DSM_Line *//* 功能：数据采样法直线插补 *//* 参数：double XEnd, double YEnd 插补终点 mm *//* double FVal 插补速度 mm/min *//* unsigned short Ts 插补周期 ms *//********************************************************************/ void DSM_Line(double XEnd, double YEnd, double FVal, unsigned short Ts){double fDeltaL,fL;double K;int bXIsBigger;double GEnd,NEnd;double GStepVal;//NStepVal;double AxisGVal,AxisNVal;double fStVel;double fDistToEnd;fStVel=FVal/300000; //插补速度 ,单位为mm/stAxisGVal=AxisNVal=0;fDeltaL=FVal*Ts/(60*1000); //一个插补周期内的合成增量,单位为毫米fL=sqrt(XEnd*XEnd+YEnd*YEnd);K=fDeltaL/fL;//确定引导坐标和非引导坐标if (fabs(XEnd>=fabs(YEnd))){bXIsBigger=1;GEnd=XEnd;NEnd=YEnd;}else{bXIsBigger=0;GEnd=YEnd;NEnd=XEnd;}GStepVal=GEnd*K;fDistToEnd=(AxisGVal-GEnd)*(AxisGVal-GEnd)+(AxisNVal-NEnd)*(AxisNVal-NEnd);while (fDistToEnd>(fDeltaL*fDeltaL/4)){AxisGVal+=GStepV al;AxisNVal=AxisGVal*NEnd/GEnd;if (bXIsBigger){InsertPoint(AxisGVal,AxisNVal);}else{InsertPoint(AxisNVal,AxisGVal);}fDistToEnd=(AxisGVal-GEnd)*(AxisGVal-GEnd)+(AxisNVal-NEnd)*(AxisNVal-NEnd);}}/********************************************************************//* 函数名: DSM_Circle *//* 功能：数据采样法圆弧插补 *//* 参数：double XStart, double YStart 插补起点 mm *//* double XEnd, double YEnd 插补终点 mm *//* double FVal 插补速度 mm/min *//* unsigned short Ts 插补周期 ms *//* double radius 圆弧半径 mm *//* bool bIsCW 圆弧插补方向 0或1 *//********************************************************************/void DSM_Circle(double xSt, double ySt, double xEnd, double yEnd,double radius, double FVal, i nt Ts, int bIsCW){double FT,a,xCur,yCur,xCur1;double es,xdir,ydir;//用于判定终点的误差int full_circle=0,judge=1;int ndir;if(xSt==xEnd&ySt==yEnd)full_circle=1;//整圆判断 FT=FVal*Ts/60/1000.0; es=FT/2;a=2*asin(FT/2/radius);//每个插补周期所超过的弦线对应的圆心角xCur=xSt,yCur=ySt;InsertPoint(xCur,yCur);if(bIsCW==0)//逆圆插补{while(judge==1||full_circle==1)//终点判断{xCur1=xCur*cos(a)-yCur*sin(a);//三角函数圆弧插补的迭代公式yCur=yCur*cos(a)+xCur*sin(a);xCur=xCur1;InsertPoint(xCur,yCur);full_circle=0;xdir=xCur-xEnd;ydir=yCur-yEnd;ndir=Judge_Quadrant(xdir,ydir);switch(ndir){case 1:judge=xdir>=es||ydir>=es;break;case 2:judge=(-xdir)>=es||ydir>=es;break;case 3:judge=(-xdir)>=es||(-ydir)>=es;break;case 4:judge=xdir>=es||(-ydir)>=es;break;}}}else//顺圆插补{while(judge==1||full_circle==1)//终点判断{xCur1=xCur*cos(a)+yCur*sin(a);//三角函数圆弧插补的迭代公式yCur=yCur*cos(a)-xCur*sin(a);xCur=xCur1;InsertPoint(xCur,yCur);full_circle=0;xdir=xCur-xEnd;ydir=yCur-yEnd;ndir=Judge_Quadrant(xdir,ydir);switch(ndir){case 1:judge=xdir>=es||ydir>=es;break;case 2:judge=(-xdir)>=es||ydir>=es;break;case 3:judge=(-xdir)>=es||(-ydir)>=es;break;case 4:judge=xdir>=es||(-ydir)>=es;break;}}}}FILE *fp;//文件指针int main(){double ft=1000.0*10/60/1000;char fn[10];printf("please input filename:\n");scanf("%s",fn);if((fp=fopen(fn,"w"))==NULL){printf("can't open file\n");exit(0);}// DSM_Circle(40,0,40,0,40,1000,10,1);//输入要插补圆弧的参数DSM_Line(30,50,1000,10);//输入要插补直线的参数fclose(fp);return 0;}。

数据采样插补算法一、数据采样插补算法的基本概念说起数据采样插补算法，你可能觉得有点复杂，但其实它说白了就是一种填补数据空缺的“巧妙办法”。

你知道的，数据在收集的过程中总会有一些缺失，或者因为各种原因出现了空白。

这就像是你做菜时，调料放多了或者放错了，结果某一味突然少了，这时候你怎么办？对了，你得想办法补回来。

数据插补也是这个道理，只不过是通过一定的数学方法，来填补那些“缺席”的数据点。

举个简单的例子，想象一下你正在做一个大数据分析，收集到的数据表上有一些空格，可能是因为设备故障，可能是因为操作失误。

怎么办呢？这时候插补算法就可以派上用场。

它就像是那个在厨房里总能找到替代品的“食材补充专家”，能精准地根据现有的数据，推测出合理的值来填补空白。

就像你看着锅里的汤，知道该加点什么，才能保持整体的美味。

这个插补过程可不简单，它需要运用一定的数学模型和统计技巧。

你可以把它想象成一个非常懂数据脾气的“厨师”，通过对已有数据的了解，来合理“调配”缺失的数据，确保最终的结果既合理又准确。

这样做，不仅能避免因为缺失数据导致的分析偏差，还能提高整体的数据质量，进而增强你分析的可信度。

1.插补算法的应用数据插补算法广泛应用于很多领域，比如医疗、金融、市场营销等。

举个例子，你在做一项关于医院病人的研究时，可能有些病人的某些数据缺失。

比如，某些病人没做某项检查，或者没提供完整的个人历史。

怎么办？通过插补算法，你可以根据其他病人的相似数据来推测这些缺失值，避免因为这些小缺失而影响整项研究的结果。

更神奇的是，这种方法不仅让你得到更完整的数据，甚至有时候能提高预测的准确性。

2.插补的基本方法常见的插补方法有很多，最简单的就是“均值插补”。

它就是把缺失的数据填上该列数据的平均值。

这就像是你做一个大锅饭，大家都吃差不多的份量，结果有一个人不小心掉了几颗米。

没关系，其他人的饭份量可以稍微补一下，最终饭量差不多。

但是，如果你的数据差距特别大，这种方法可能就不太靠谱了。