江苏省南通市通州区2012年高一数学暑假自主学习 单元检测十二 综合试卷2

2012年高一上册数学期中测试卷(含答案)江苏省南通第一中学2012―2013学年度第一学期期中考试卷高一数学说明 1．本试卷满分160分，考试时间120分钟； 2．在答题纸的密封线内填写班级、姓名、考号，在右下角填上座位号，密封线内不要答题； 3．请将所有答案按照题号填写在答题纸相应的答题处，否则不得分．一、填空题：本大题共14小题，每小题5分，共70分，请把答案填写在答题纸相应的位置上 1．若，则▲ ． 2．函数的定义域是▲ ． 3．已知幂函数的图象过点，则▲ ． 4．设函数满足，则的表达式是▲ ． 5．函数的值域是▲ ． 6．若 , ,则用“＞”将按从大到小可排列为▲ ． 7．已知函数，则▲ ． 8．若函数在区间上的最大值与最小值之和为，则a的值为▲ ． 9．给定函数：① ,② ,③ ,④ ，其中在区间上是单调减函数的序号是▲ ．（填上所有你认为正确的结论的序号） 10．已知方程的解所在区间为，则= ▲ ． 11．已知函数在区间上是减函数，则的取值范围是▲ ． 12．定义在实数集R上的奇函数满足：① 在内单调递增，② ，则不等式的解集为▲ ． 13．已知函数，当时，恒成立，则实数的取值范围是▲ ． 14．已知函数，现给出下列命题：① 当其图象是一条连续不断的曲线时，则 = ；② 当其图象是一条连续不断的曲线时,能找到一个非零实数使在上是增函数；③ 当时，不等式恒成立；④ 函数是偶函数．其中正确命题的序号是▲ ．（填上所有你认为正确的命题的序号）二、解答题：本大题共6小题，共计90分，请在答题纸相应的位置上作答，解答时应写出文字说明、证明或演算步骤 15．（本小题满分14分）设全集 R，集合，．（1）求；（2）若集合，满足，求实数的取值范围 16．（本小题满分14分）（1）计算的值；（2）已知，求和的值． 17．（本小题满分15分）已知为定义在R上的奇函数，当时，为二次函数，且满足，在上的两个零点为和．（1）求函数在R上的解析式；（2）作出的图象，并根据图象讨论关于的方程根的个数． 18．（本小题满分15分）已知函数，其中，记函数的定义域为D．（1）求函数的定义域D；（2）若函数的最小值为，求的值；（3）若对于D内的任意实数 ,不等式＜恒成立,求实数的取值范围．19．（本小题满分16分）已知函数（ R）．（1）试判断的单调性，并证明你的结论；（2）若为定义域上的奇函数，① 求函数的值域；② 求满足的的取值范围．20．（本小题满分16分）若函数满足下列条件：在定义域内存在使得成立，则称函数具有性质；反之，若不存在，则称函数不具有性质．（1）证明：函数具有性质，并求出对应的的值；（2）已知函数具有性质，求的取值范围；（3）试探究形如：① ,② ,③,④ ,⑤ 的函数，指出哪些函数一定具有性质 ?并说明理由．江苏省南通第一中学2012―2013学年度第一学期期中考试高一数学参考答案一、填空题：本大题共14小题，每小题5分，共70分，请把答案填写在答题纸相应的位置上. 1． 2． 3．9 4．（或写成）5． 6．c＞a＞b 7．4 8． 9．②④ 10．4 11．a≤ 12． 13． 14．①③ 二、解答题：本大题共6小题，共计90分，请在答题纸相应的位置上作答，解答时应写出文字说明、证明或演算步骤. 15．（本小题满分14分）解：（1）∵ ∴ ……………………………………4分∴ ……………………………………7分（2）由得……………………………………9分根据数轴可得，……………………………………12分从而……………………………………14分16．（本小题满分14分）解：（1）原式 (4)分…………………………………7分（2）…………………………………10分∵ ∴由得…………………………………14分（注：不指出得扣1分；直接得扣2分）17．（本小题满分15分）解：（1）由题意，当时，设，，∴ ，∴ .................................2分（注：设一样给分）当时，，∵ 为上的奇函数，∴ ，∴ 即时， (5)分当时，由得：……………………………6分所以．……………………………7分（2）作出的图象（如图所示）…………………10分（注：的点或两空心点不标注扣1分，不要重复扣分）由得：，在图中作，根据交点讨论方程的根：当或时，方程有个根；………………………………………11分当或时，方程有个根；………………………………………12分当或时，方程有个根；………………………………………13分当或时，方程有个根；………………………………………14分当时，方程有个根．………………………………………15分18．（本小题满分15分）解：（1）要使函数有意义：则有，解得∴ 函数的定义域D为………………………………………2分（2），，即，…………5分由，得，．……………………………7分（注：不化简为扣1分）（3）由题知－x2+2mx－m2+2m＜1在x∈ 上恒成立，－2mx+m2－2m+1＞0在x∈ 上恒成立，……………………………8分令g(x)=x2－2mx+m2－2m+1，x∈ ，配方得g(x)=(x－m)2－2m+1，其对称轴为x=m，①当m≤－3时， g(x)在为增函数，∴g(－3)= (－3－m)2－2m+1= m2+4m +10≥0，而m2+4m +10≥0对任意实数m恒成立，∴m≤－3．………………………10分②当－3＜m＜1时，函数g(x)在（－3,－1）为减函数，在（－1, 1）为增函数，∴g(m)=－2m+1＞0，解得m＜∴－3＜m ＜…………………12分③当m≥1时，函数g(x)在为减函数，∴g(1)= (1－m)2－2m+1= m2－4m +2≥0，解得m≥ 或m≤ ，∴－3＜m＜…………………14分综上可得，实数m的取值范围是 (－∞，)∪[ ，+∞) …………………15分19．（本小题满分16分）解：（1）函数为定义域(－∞，+∞)，且，任取 (－∞，+∞)，且则………………3分∵ 在上单调递增，且∴ ，，，，∴ ，即，∴ 在(－∞，+∞)上的单调增函数．.....................5分（2）∵ 是定义域上的奇函数，∴ ，即对任意实数恒成立，化简得，∴ ，即，..................8分（注：直接由得而不检验扣2分）①由得，∵ ，∴ ， (10)分∴ ，∴ 故函数的值域为．………………………………………………12分②由得，且在(－∞，+∞)上单调递增，∴ ，…………………………14分解得，故的取值范围为．……………………………………………………16分20．（本小题满分16分）解：（1）证明：代入，得：，即，……………………………………2分解得，∴函数具有性质．…………………………………3分（2）的定义域为R，且可得，]∵ 具有性质，∴存在，使得 ,代入得，化为，整理得: 有实根，……………………………5分①若 ,得，满足题意；……………………………………………6分②若 ,则要使有实根，只需满足，即，解得，∴ ，综合①②,可得………………………………………8分（3）解法一：函数恒具有性质，即关于的方程（*）恒有解. ………………………………………9分①若，则方程（*）可化为整理，得，当时，关于的方程（*）无解，∴ 不恒具备性质；………………………………………10分②若，则方程（*）可化为，解得，∴函数一定具备性质；…………………12分③若，则方程（*）可化为无解，∴ 不具备性质；……………………………………………13分④若，则方程（*）可化为，化简得，当时，方程（*）无解，∴ 不恒具备性质；…………………………14分⑤若，则方程（*）可化为，化简得，显然方程无解，∴ 不具备性质；…………………………15分综上所述，只有函数一定具备性质．…………16分（注：第（3）问直接得一定具备性质而不说明理由只给1分）。

综合试卷1、填空题：本大题共14题，每小题5分，共70分.1 •若0 m, m22m，则实数m的值为________________ .2 .已知f(x) = ax3+bsinx+1，且f(—1) = 5,贝U f(1) = __________ .3. 已知不等式ax2—bx + 2 v 0 的解集为｛x|1 v x v 2｝，贝U a = _______ , b = ________ .4. 已知a n是等差数列，a415 , S5 55，则过点P(3, a3), Q(4, aj的直线的斜率__________ 5.若函数y=f(x)的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，然后再将整1 个图象沿x轴向左平移2个单位，沿y轴向下平移1个单位，得到函数y=?sinx的图象，则y=f(x)是 _______________.6 .在样本的频率分布直方图中，共有4个长方形，这4个小长方形的面积由小到大构成等差数列｛a n｝，已知a2 = 2a1，且样本容量为400，则小长方形面积最大的一组的频数为__________ .27 .已知sin( ) a ,则cos( )的值为6 3&对于下列的伪代码(n€ N*),给出如下判断：①当输入n=2时，输出结果为1;②当输入n=3时，输出结果为1;③当输入n =99时，输出结果一定是非负的.其中所有正确命题的序号为____________ .9.在等腰直角三角形ABC的斜边AB上随机取一点M,则/ ACM < 30的概率为___________ .10 .在△ ABC中，a, b, c分别是角A, B, C的对边，若a2, b2, c2成等差数列，则cosB的最小值为_____________ .11.如图，设P是单位圆和x轴正半轴的交点，M、N是单位圆上的两点，O是坐标原点，POM— , POM ,3uumr uuir[0, ] , f( ) OM ON，则f()的范围为a J 1:b J 2；Read n:For I From 1To:n； c J a — b i p J a: a J b: b J p:End For；If c >0 Then ；Print c ■ Else: c J —c ; Print c :End12 .设点A(1,0), B(2,1),如果直线ax by 1与线段AB有2 2 公共点,那么a b的最小值为 .13 •数列a n中，a i 6，且a n a n 1 空n 1 ( n N* , n > 2 )，则这个数列的通项公n式a n _________________ .14 •已知函数f x 2x 3，若0 2a b 1，且f 2a f b 3，则T 3a2b的取值范围为________________ .二、解答题：本大题共6小题，共90分，解答应写出文字说明、证明过程或演算步骤.15 .(本小题满分14分)已知集合A x x22x 8<0 , B xx2(2m 3)x m23m<0, m R .(1 )若AI B 2, 4，求实数m的值；(2)设全集为R，若A sB，求实数m的取值范围.16 .(本小题满分14分)已知ABC中，a,b,c分别是角A,B,C所对的边，且『ac，向量m cos A C ,1和n 1,cos B 满足m n 3.2(1 )求sinAsinC 的值；(2)求证：ABC为等边三角形.17 .(本小题满分14分)已知函数 f (x) 3 2log 2 x, g(x) log 2 x .(1)当x 1,4时，求函数h(x) f (x) 1 g(x)的值域；(2)如果对任意的x 1,4 ,不等式f(x2) f(「x) k g(x)恒成立，求实数k的取值范围.18 .(本小题满分16分)在平面直角坐标系中，已知矩形ABCD的长为2，宽为1, AB、AD 边分别在x轴、y轴的正半轴上，A点与坐标原点重合(如图所示)。

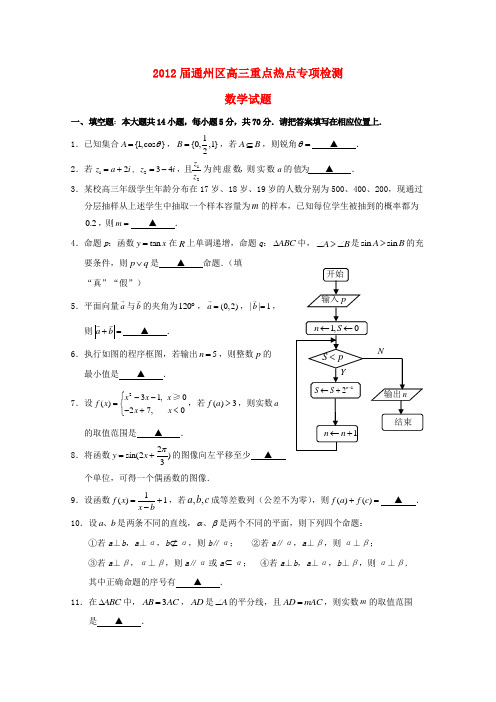
2012届通州区高三重点热点专项检测数学试题一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在相应位置上．1．已知集合{1,cos }A θ=，1{0,,1}2B =，若A B ⊆，则锐角θ= ▲ ．2．若 12z a i =+, 234z i =-，且12zz 为 纯 虚 数，则 实 数 a 的 值为 ▲ ．3．某校高三年级学生年龄分布在17岁、18岁、19岁的人数分别为500、400、200，现通过分层抽样从上述学生中抽取一个样本容量为m 的样本，已知每位学生被抽到的概率都为0.2，则m = ▲ ．4．命题p ：函数tan y x =在R 上单调递增，命题q ：ABC ∆中，A B ∠>∠是sin sin A B >的充要条件，则p q ∨是 ▲ 命题．（填“真”“假”）5．平面向量a 与b 的夹角为120︒，(0,2)a =，||1b =， 则a b += ▲ ．6．执行如图的程序框图，若输出5n =，则整数p 的 最小值是 ▲ ．7．设231,0()27,0x x x f x x x ⎧--=⎨-+<⎩≥，若()3f a >，则实数a的取值范围是 ▲ ． 8．将函数2sin(2)3y x π=+的图像向左平移至少 ▲ 个单位，可得一个偶函数的图像． 9．设函数1()1f x x b=+-，若,,a b c 成等差数列（公差不为零），则()()f a f c += ▲ ． 10．设a b 、是两条不同的直线，αβ、是两个不同的平面，则下列四个命题：①若a ⊥b ，a ⊥α，b ⊄α，则b ∥α； ②若a ∥α，a ⊥β，则α⊥β； ③若a ⊥β，α⊥β，则a ∥α或a ⊂α； ④若a ⊥b ，a ⊥α，b ⊥β，则α⊥β． 其中正确命题的序号有 ▲ ．11．在ABC ∆中，3AB AC =，AD 是A ∠的平分线，且AD mAC =，则实数m 的取值范围 是 ▲ ．12．设函数2()sin (,)3sin f x x m x R m R x=++∈∈+最大值为()g m ，则()g m 的最小值为▲ ．13．已知,a b R ∈，1C ：2224250x y x y a +-+-+=与2C ：22(210)2x y b x by +---+2210160b b -+=交于不同两点1122(,),(,)A x y B x y ，且121212120x x y y y y x x -++=-+，则实数b 的值为 ▲ ．14．已知等比数列{}n a 满足11a =，102q <<，且对任意正整数k ，12()k k k a a a ++-+仍是该数列中的某一项，则公比q 的取值集合为 ▲ ．二、解答题：本大题共六小题，共计90分．请在指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知向量(sin ,2)a θ=-与(1,cos )b θ=互相垂直，其中(0,)2πθ∈．（1）求sin θ和cos θ的值； （2）若sin()(0,)2πθϕϕ-=∈，求cos ϕ的值．16．（本小题满分14分）已知PA ⊥矩形ABCD所在平面，PA AD ==，E 为线段PD 上一点，G 为线段PC 的中点．（1）当E 为PD 的中点时，求证：BD CE ⊥； （2）当2PEED=时，求证：BG //平面AEC ．17．（本小题满分14分）某创业投资公司拟投资开发某种新能源产品，估计能获得10万元～1000万元的投资收 益．现准备制定一个对科研课题组的奖励方案：奖金y （单位：万元）随投资收益x （单 位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%．现PABC DEG有两个奖励方案的函数模型：（1）2150xy =+；（2）4lg 3y x =-．试问这两个函数模 型是否符合该公司要求，并说明理由．18．（本小题满分16分）已知椭圆2222:1x y C a b +=(0)a b >>上的一动点P 到右焦点的最短距离为2焦点到右准线的距离等于短半轴的长． （1）求椭圆C 的方程；（2）设()4,0P ，,A B 是椭圆C 上关于x 轴对称的任意两个不同的点，连结PB 交椭圆C 于另一点E ，证明直线AE 与x 轴相交于定点Q ；（3）在（2）的条件下，过点Q 的直线与椭圆C 交于,M N 两点，求OM ON ⋅的取值 范围．19．（本小题满分16分） 函数ln ()a xf x x x=-，其中a 为常数． （1）证明：对任意a R ∈，函数()y f x =图像恒过定点；（2）当1a =时，不等式()20f x b +≤在(0,)x ∈+∞上有解，求实数b 的取值范围； （3）若对任意[),0a m ∈时，函数()y f x =在定义域上恒单调递增，求m 的最小值．20．（本小题满分16分）数列{}n a 中，11a =，37a =，且11(2)1n n na a n n +-=-≥． （1）求2a 及{}n a 的通项公式；（2）设k a 是{}n a 中的任意一项，是否存在,()r p N r p k *∈>>，使,,k p r a a a 成等比 数列？如存在，试分别写出p 和r 关于k 的一个．．表达式，并给出证明； （3）证明：对一切n N *∈，21176ni i a =<∑．2012届高三重点热点专项检测数学附加题21．本题包括高考A ，B ，C ，D 四个选题中的B ，C 两个小题，每小题10分，共20分．把答案写在答题卡相应的位置上．解答时应写出文字说明、证明过程或演算步骤． B ．选修4—1：矩阵与变换已知二阶矩阵A 有特征值11λ=及对应的一个特征向量111⎡⎤=⎢⎥⎣⎦e 和特征值22λ=及对应的一个特征向量210⎡⎤=⎢⎥⎣⎦e ，试求矩阵A ．C ．选修4—4：极坐标与参数方程将参数方程cos sin ,(sin 2x y θθθθ=+⎧⎨=⎩为参数)化为普通方程．22．【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤．由数字1，2，3，4组成五位数12345a a a a a ，从中任取一个．（1）求取出的数满足条件：“对任意的正整数()15j j ≤≤，至少存在另一个正整数 (15k k ≤≤，且)k j ≠，使得j k a a =”的概率；（2）记ξ为组成该数的相同数字的个数的最大值，求ξ的概率分布列和数学期望．23．【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤．求证：对于任意的正整数n ，(2n s N *∈. 2012届高三重点热点专项检测数学参考答案及评分标准一、填空题：本大题共14小题，每小题5分，共70分．1．3π 2．83 3．220 4．真 5．8 7．{|0a a <或}4a >8．512π 9．2 10．①②③④ 11．3(0,)2 12．34 13．53 14．1}二、解答题：本大题共6小题，共90分． 15．解：（1）∵a b ⊥，∴sin 2cos 0θθ-=，又22sin cos 1θθ+=，且(0,)2πθ∈，∴sin θ，cos θ=． …………………………6分（2）∵(0,)2πθ∈，(0,)2πϕ∈，∴(,)2ππθϕ-∈-，又sin()θϕ-=，∴cos()θϕ- …………………………10分∴[]cos cos ()ϕθθϕ=--cos cos()sin sin()θθϕθθϕ=-+-2==． …………………………14分 16．（1）过点E 作EQ AD ⊥于Q ，连结CQ ，则tan CD DBC BC ∠==tan DQ QCD CD ∠==，所以DBC QCD ∠=∠，又90QDC BCD ∠=∠=︒， ∴Rt DBC Rt QCD ∆∆，则易得BD CQ ⊥． ∵PA ⊥平面ABCD ，∴PA BD ⊥，又//PA EQ ，∴BD EQ ⊥，又CQ EQ Q =，∴BD ⊥平面ECQ ，∴BD CE ⊥. …………………………7分 （2）取PE 的中点F ，连接GF ，BF ， ∵G 为PC 的中点，∴GF //CE ，又GF ⊄平面ACE ，CE ⊂平面ACE ， ∴GF //平面ACE ，连接BD 交AC 与点O ，连接OE ． ∵E 为DF 的中点，∴BF //OE ，又BF ⊄平面ACE ，OE ⊂平面ACE ∴BF //平面ACE ，∵F GF BF = ， ∴平面BGF //平面AEC .又BG BGF ⊂平面，∴BG //平面AEC ． …………………………14分17．解：设奖励函数模型为y ＝f (x )，由题意可知该公司对函数模型应满足下列条件：当x ∈[10，1000]时，①f (x )是增函数；②f (x )≤9恒成立；③1()5f x x ≤恒成立．①对于函数模型()2150xf x =+：当x ∈[10，1000]时，f (x )是增函数，则max 100020()(1000)2291503f x f ==+=+<．所以f (x )≤9恒成立． …………………………3分因为函数()12150f x x x =+在[10，1000]上是减函数，所以max()121150105f x x ⎡⎤=+>⎢⎥⎣⎦． 从而1()5f x x ≤不恒成立．故该函数模型不符合公司要求． …………………………7分 ②对于函数模型f (x )＝4lg x －3：当x ∈[10，1000]时，f (x )是增函数，则max ()(1000)4lg100039f x f ==-=．所以f (x )≤9恒成立． …………………………9分设g (x )＝4lg x －35x -，则4lg 1()5e g x x '=-.当x ≥10时，24lg 12lg 1lg 1()0555e e e g x x --'=-=<≤，所以g (x )在[10，1000]上是减函数，从而g (x )≤g (10)＝－1＜0，所以4lg x －35x -＜0，即4lg x －3＜5x ，所以1()5f x x ≤恒成立．故该函数模型符合公司要求． …………………………14分18．解：（1）由题意知222a c a c bc ⎧-=-⎪⎨-=⎪⎩， 解得22a b =⎧⎪⎨=⎪⎩，故椭圆C 的方程为22142x y +=． …………………………4分（2）由题意知直线PB 的斜率存在，设直线PB 的方程为(4)y k x =-． 由22(4),1.42y k x x y =-⎧⎪⎨+=⎪⎩ 得2222(21)163240k x k x k +-+-=． ①设点11(,)B x y ，22(,)E x y ，则11(,)A x y -．直线AE 的方程为212221()y y y y x x x x +-=--． 令0y =，得221221()y x x x x y y -=-+．将11(4)y k x =-，22(4)y k x =-代入，整理，得12121224()8x x x x x x x -+=+-． ②由①得 21221621k x x k +=+，212232421k x x k -=+代入②整理，得1x =．所以直线AE 与x 轴相交于定点(1,0)Q ． …………………………10分 （3）当过点Q 直线MN 的斜率存在时，设直线MN 的方程为(1)y m x =-，(,)M M M x y ，(,)N N N x y ．由22(1),1.42y m x x y =-⎧⎪⎨+=⎪⎩ 得2222(21)4240m x m x m +-+-=．∴22421M N m x x m +=+，222421M N m x x m -=+， 22321M N m y y m =-+．则M N M N OM ON x x y y ⋅=+222222224341712121212221m m m m m m m -+=-=-=--⋅++++． 因为20m ≥，所以21711422212m ---⋅<-+≤．所以1[4,)2OM ON ⋅∈--．当过点Q 直线MN 的斜率不存在时，其方程为1x =．解得6M ，6(1,N ．此时12OM ON ⋅=-．所以OM ON ⋅的取值范围是1[4,]2--． …………………………16分19．解：（1）令ln 0x =，得1x =，且(1)1f =，∴函数()y f x =图像恒过定点(1,1)． …………………………2分（2）当1a =时，ln ()xf x x x=-，∴21ln ()1xf x x-'=-，即22ln 1()x x f x x +-'=， 令()0f x '=，得1x =．x(0，1) 1 （1，＋∞）()f x '－ 0 ＋ f (x )极小值∴min ∵()20f x b +≤在(0,x ∈+∞）上有解，∴min 2()b f x -≥，即21b -≥，∴实数b 的取值范围为1(,]2-∞-．…………………9分（3）2ln ()1a a xf x x-'=-，即22ln ()x a x a f x x +-'=，令2()ln g x x a x a =+-，由题意可知，对任意[,0)a m ∈，()f x '≥0在(0,)x ∈+∞恒成立， 即2()ln 0h x x a x a =+-≥在(0,)x ∈+∞恒成立．∵22()2a x ah x x x x+'=+=，令()0h x '=，得x =∴min 3()02h x h a ⎛⎫== ⎪ ⎪⎝⎭≥，解得32a e -≥． ∴m 的最小值为32e -． …………………16分20．解：（1）23211a a -=，故24a =． …………………1分2n ≥时，1111()111n n n a a a n n n n n n+-==----- ∴1111n n a a n n +--=-，∴11n a n -⎧⎫⎨⎬-⎩⎭为常数列． ………………………4分 ∴141121n a n --=--，所以32(2)n a n n =-≥． 又11a =也满足上式，∴{}n a 的通项公式为32()n a n n N *=-∈． ………………………6分（2）当42p k =-，1610r k =-时满足,,k p r a a a 成等比数列． 证明如下：424(32)p k a a k -==-，161016(32)r k a a k -==-，显然,,k p r a a a 成等比数列． …………………………10分 （3）证明：2k ≥时， 22111111()(32)(34)(31)33431k a k k k k k =<=------， …………………12分 ∴当2n ≥时， 221211111111111325583431n ni i i i a a n n ==⎡⎤⎛⎫⎛⎫⎛⎫=+<+-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎝⎭⎣⎦∑∑ 1117132316n ⎛⎫=+-< ⎪-⎝⎭． …………………………15分又1n =时，211716a =<，∴对一切n N *∈，21176ni ia =<∑． …………………16分附加题参考答案21B ．解：设矩阵a b A c d ⎡⎤=⎢⎥⎣⎦，其中a b c d ∈R ,,,， 因为11⎡⎤⎢⎥⎣⎦是矩阵A 的属于11λ=的特征向量，则有110110a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ ①， 又因为10⎡⎤⎢⎥⎣⎦是矩阵A 的属于22λ=的特征向量，则有210100a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ ②， …6分由①②得1010200a b c d a c --=⎧⎪-+-=⎪⎨-=⎪⎪-=⎩,,,,……………8分解得2101a b c d ==-==,,,,因此2101A -⎡⎤=⎢⎥⎣⎦， ……………10分 21C ．解：cos sin (1)sin 2(2)x y θθθ=+⎧⎨=⎩，将(1)式平方得21sin 2(3)x θ=+， 将（2）式代入（3）式得21x y =+， ……………8分所以所求的普通方程为21(y x x =-. ……………10分 22．解：（1）由数字1,2,3,4组成的五位数12345a a a a a 共有54个数，满足条件的数分为两类：①只有一个数组成共有4个；②由两个数字组成，共有22452120C C ⋅⋅=个， ∴所求的概率为5124314256p ==. ……………4分（2） ξ的可能取值为2,3,4,5，则1332124543545150(2)4256C A C C C C P ξ⋅+⋅⋅⋅===， 312545390(3)4256C C P ξ⋅⋅===， 411543515(4)4256C C C P ξ⋅⋅===， 541(5)4256P ξ===. ……………6分 ∴ξ的分布为：∴6352(2)3(3)4(4)5(5)256EP P P P ξξξξξ=⋅=+⋅=+⋅=+⋅==. ……………9分 答：ξ的数学期望为635256． ……………10分 23．解：由二项式定理可知，1201122(22222nn nn n nn n n n C C C C --=++++,设(2n x =，而若有(2n +=,ab N *∈，则(2n =,a b N *∈， …………………6分∵(2(21n n ⋅=+⋅-=，∴令,a s s N *=∈，则必有1b s =-． …………………9分 ∴(2n s N *∈． …………………10分 注：本题也可用数学归纳法证明，证明正确的也给相应的分数．。

2012—2013学年第一学期通州区三星级高中期中联考高一数学试题试题总分：160分 考试时间：120分钟一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置．．．．．．．． 1. 集合{}1,1-=A 的子集的个数为 ▲ ．2. 已知f (x )＝x 2＋ax ＋b ，满足f (1)＝0，f (2)＝0，则f (－1)= ▲ ． 3. 函数)4lg(2x x y -++=的定义域为 ▲ ． 4. 已知0m >，化简21334(2)m m -÷的结果为 ▲ ．5. 对应:f A B →是集合A 到集合B 的映射，若集合{}1,0A =-，{}1,2B =，则这样的映射有 ▲ 个．6. 已知函数⎩⎨⎧<≥=)0(2)0(2)(x x x x f x 则=-))1((f f ▲ ．7. 计算：12839()log 9log 324-+⨯= ▲ ．8. 已知函数()f x 由下表给出，则满足(())2f f x ≤的x 的值是 ▲ ．9. 某班共30人，其中15人喜爱篮球运动，10人喜爱兵乓球运动，8人对这两项运动都不喜爱，则 喜爱篮球运动但不喜爱乒乓球运动的人数为 ▲ ． 10. 已知5.02.12.05.1,8.0log ,3.0log ===c b a , 则将c b a ,,按从小到大的顺序排列为 ▲ ．11. 若函数2)21()(1+=-x x f 的图像恒过定点 ▲ ．12. 已知)(x f y =是定义在R 上的奇函数，且当0>x 时，x x f 21)(+=，则=)8(log 21f ▲ ．13．若,,,2121x x R x x ≠∈则下列性质对函数x x f 2)(=成立的序号是 ▲ ． ①);()()(2121x f x f x x f ⋅=+ ②);()()(2121x f x f x x f +=⋅ ③;0)()]()([2121>-⋅-x x x f x f ④).2(2)()(2121x x f x f x f +>+ 14. 下列说法正确的有 ▲ ．（填序号）①若函数()f x 为奇函数，则(0)0f =；②函数1()1f x x =-在(,1)(1,)-∞+∞U 上是单调减函数；③若函数(21)y f x =+的定义域为[2,3]，则函数()f x 的定义域为1[,1]2；④要得到(21)y f x =-的图象，只需将(2)y f x =的图象向右平移12个单位.二、解答题：本大题共6小题，共计90分．请在答卷纸指定区域内．．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 15. (本小题满分14分)设全集为R ，集合{}63≥≤=x x x A 或,{}92<<-=x x B .（1）求B A Y ，(∁U A)I B ；（2）已知{}1+<<=a x a x C ，若B C ⊆,求实数a 的取值范围.16. (本小题满分14分)化简与求值 （143342(0,0)()a b a b a b->>⋅；（2）02221log log 12log 42(1)2---.17. (本小题满分14分)已知某皮鞋厂一天的生产成本C （元）与生产数量n （双）之间的函数关系是400050.C n =+ （1）如果某天的生产成本是36000元，问这一天生产了多少双皮鞋？（2）若每双皮鞋的售价是90元，且生产的皮鞋全部售出，试写出这一天的利润P 关于这一天生产数量n 的函数表达式，并求出每天至少生产多少双皮鞋，才能保证每天的利润不低于8500元？18. (本小题满分16分)函数).(1212)(R x x f x x ∈+-=（1）判断并证明函数)(x f 的单调性； （2）判断并证明函数)(x f 的奇偶性； （3）解不等式.0)32()1(<-+-m f m f19. (本小题满分16分)二次函数)(x f 的图像顶点为),16,1(A 且图像在x 轴上截得线段长为8. （1）求函数)(x f 的解析式；（2）令),()22()(x f x a x g --=若)(x g 在区间]2,0[上的最大值是5，求实数a 的值.20. (本小题满分16分)已知集合M 是满足下列性质的函数)(x f 的全体：在定义域D 内存在0x ，使得 )1()()1(00f x f x f +=+成立.（1）函数xx f 1)(=是否属于集合M ?说明理由； （2）若函数b kx x f +=)(属于集合M ，试求实数k 和b 的取值范围；（3）设函数1lg )(2+=x ax f 属于集合M ，求实数a 的取值范围．2012—2013学年第一学期通州区三星级高中期中联考高一数学参考答案及评分标准一、填空题: 本大题共14小题，每小题5分，共70分. 1.集合{}1,1-=A 的子集的个数为 ▲ . 42. 已知f (x )＝x 2＋ax ＋b ，满足f (1)＝0，f (2)＝0，则f (－1)= ▲ ． 6 3. 函数)4lg(2x x y -++=的定义域为 ▲ . )4,2[- 4. 已知0m >，化简21334(2)m m -÷的结果为 ▲ ．2m5. 对应:f A B →是集合A 到集合B 的映射，若集合{}1,0A =-，{}1,2B =，则这样的映射有 ▲ 个．46. 已知函数⎩⎨⎧<≥=)0(2)0(2)(x x x x f x则=-))1((f f ▲ . 17. 计算：=⨯+-32log 9log )49(3821▲ . 48. 已知函数()f x 由下表给出，则满足(())2f f x ≤的x 的值是 ▲ . 2，39. 某班共30人，其中15人喜爱篮球运动，10人喜爱兵乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为 ▲ . 1210. 已知5.02.12.05.1,8.0log ,3.0log ===c b a , 则将c b a ,,按从小到大的顺序排列为 ▲ .b <a <c11. 若函数2)21()(1+=-x x f 的图像恒过定点 ▲ . （1,3）12. 已知)(x f y =是定义在R 上的奇函数，且当0>x 时，x x f 21)(+=，则=)8(log 21f ▲ . -913.若,,,2121x x R x x ≠∈则下列性质对函数x x f 2)(=成立的序号是 ▲ .①③④ ①);()()(2121x f x f x x f ⋅=+ ②);()()(2121x f x f x x f +=⋅ ③;0)()]()([2121>-⋅-x x x f x f ④).2(2)()(2121x x f x f x f +>+14. 下列说法正确的有 ▲ ．（填序号）④①若函数()f x 为奇函数，则(0)0f =；②函数1()1f x x =-在(,1)(1,)-∞+∞U 上是单调减函数；③若函数(21)y f x =+的定义域为[2,3]，则函数()f x 的定义域为1[,1]2；④要得到(21)y f x =-的图象，只需将(2)y f x =的图象向右平移12个单位. 二、解答题: 本大题共6小题，计90分，解答应写出必要的文字说明，证明过程或演算步骤． 15. （本题14分）设全集为R ，集合 {}63≥≤=x x x A 或,{}92<<-=x x B . （1）求B A Y ，(∁U A)I B ；（2）已知{}1+<<=a x a x C ，若B C ⊆,求实数a 的取值范围. 解：（1）A B U =R ………………………3分∁U A =}63{<<x x ，∴ （∁U A ） {}63<<=x x B I …………9分 （2）∵{}|1C x a x a =<<+，且C B ⊆, ∴219a a ≥-⎧⎨+≤⎩…………12分∴所求实数a 的取值范围是82≤≤-a …………14分 16.（本题14分）化简与求值 （143342(0,0)()a b a b a b->>⋅；（2）02221log log 12log 42(1)2---.（1）1ab - …………7分；（2）32-…………7分。

高一数学暑期自主学习单元检测一直线与方程一、填空题：本大题共14 题，每题 5 分，共 70 分．1．直线 l ： ax ＋y － 2－ a ＝0 在 x 轴和 y 轴上的截距相等，则a 的值是 ______．2．若直线的倾斜角的余弦值为 4______5，则与此直线垂直的直线的斜率为．3．两条直线 ax ＋ y － 4＝ 0 与 x － y － 2 ＝ 0 订交于第一象限，则实数 a 的取值范围是 ______．4．设直线 l 与 x 轴的交点是 P ，且倾斜角为α，若将此直线绕点P 按逆时针方向旋转 45°，获得直线的倾斜角为α＋45°，则 α 的取值范围为 ______ ．5．直线 x cos α ＋3y ＋ 2＝ 0 的倾斜角的范围是 ______．6．已知点 A ( － 2,4) 、 B (4,2) ，直线 l 过点 P (0 ，－ 2) 与线段 AB 订交，则直线 l 的斜率 k 的取值范围是 ____ __ ．7．已知直线 l 1：y ＝ 2x ＋3，直线 l 2 与 l 1 对于直线 y ＝－ x 对称，则直线 l 2 的斜率为 ____ __．8．过点(1,2) 作直线l ，使直线l 与点(2,3) 和点(4 ，－ 5) 距离相等，则直线 l的方程为PMN____ __ ．9．如图，已知 A (4 ，0) 、B (0,4) ，从点 P (2,0) 射出的光芒经直线AB 反射后再射到直线 OB上，最后经直线 OB 反射后又回到 P 点，则光芒所经过的行程是 ____ __．10．一条直线过点P (1,2) 且被两条平行直线4x ＋ 3y ＋ 1＝ 0 和 4x ＋ 3y ＋ 6＝ 0 截取的线段长为2，求这条直线的方程______ ．11．设 l 的倾斜角为π 绕其上一点 P 沿逆时针方向旋转 α 角得直线 l，1α， α∈(0 ， 2 ) ， l12l 2的纵截距为－ 2，2 绕P 沿逆时针方向旋转 π－ α 角得直线 l 3： ＋ 2 － 1＝0，则 l 1的方l2 x y程为 ________．12．已知 b >0，直线 ( b 2＋1) x ＋ ay ＋ 2＝ 0 与直线 x － b 2y ＝ 0 相互垂直，则 ab 的最小值等于_______．13．已知△ ABC 的两个极点坐标为 B (1,4) 、 C (6,2) ，极点 A 在直线 x － y ＋ 3＝0 上，若△ ABC的面积为 21. 则极点 A 的坐标为 ____ __ ．14．已知 0<k <4，直线 l1：kx －2y － 2k ＋8＝ 0 和直线 l2：2x ＋ k 2y － 4k 2－ 4＝ 0 与两坐标轴围成一个四边形，则使得这个四边形面积最小的k 值为 ______ ．二、解答题：本大题共 6 小题，共90 分，解答应写出文字说明、证明过程或演算步骤．15． ( 本小题满分 14 分)已知两直线 l 1：＋ y sin θ －1＝0 和l 2：2 x sinθ ＋ y ＋ 1＝0，试求θ 的值，使得：(1) l 1 ∥ 2；xl(2)l 1⊥ l 2．16． ( 本小题满分14 分 )已知直线 l 与两坐标轴围成的三角形面积为3，分别求知足以下条件的直线l 的方程：（ 1）斜率为1的直线；（2）过定点A( 3,4)的直线. 617． ( 本小题满分14 分 )已知三条直线l 1：4x＋ y－4＝0，l 2： mx＋ y＝0及 l 3：2x－3my－4＝0，求 m的值，使 l 1，l 2， l 3三条直线能围成三角形．18． ( 本小题满分16 分 )已知三直线l 1：2x－＋＝ 0(a＞ 0) ，直线l2：－4＋2 ＋1＝0 和l3：＋－1＝0 且l1 y a x y x y与 l 2的距离是75．10(1)求 a 的值；(2) 可否找到一点P，使 P 同时知足以下三个条件：① P 是第一象限的点；②P 点到 l 1的距离是 P 点到 l距离的1的距离与 P 点到 l的距离之比是 2∶5？若能，求出P22；③ P 点到 l13点的坐标；若不可以，说明原因．19． ( 本小题满分16 分 )已知直线 l ：kx－ y＋1＋2k＝0( k∈ R)．(1)证明：直线 l 过定点；(2) 若直线不经过第四象限，求k 的取值范围；(3)若直线 l 交 x 轴负半轴于 A，交 y 轴正半轴于 B，△ AOB的面积为 S，求 S的最小值并求此时直线 l 的方程．20． ( 本小题满分16 分 )将一块直角三角板ABO （45o角）置于直角坐标系中，已知AB OB 1, AB OB ，点 P( 1,1) 是三角板内一点，现因三角板中部分（POB ）受破坏，要把破坏的部分锯掉，2 4可用经过 P 的随意向来线MN （M、N可分别与O、B重合）将其锯成AMN ．(1)求直线 MN 的斜率的取值范围；(2)uuur uuurMN 能否存在，如不存在，请说明原因；若存若 P点知足MP 1 PN，这样的直线3在，求出此时直线 MN 的方程；(3)怎样确立直线 MN 的斜率，才能使锯成的AMN 的面积最大和最小，并求出最值？MP A NO B高一数学暑期自主学习单元检测一参照答案一、填空题：a ＋ 21．答案：－ 2 或 1分析：由 a ＋2＝a ，∴ a ＝－ 2 或 1．44 π2．答案：－ 3分析：设直线的倾斜角为θ ，由题意知， cos θ＝ 5，θ∈(0 ， 2 ) ， 3 sin θ 3 4∴ sin θ＝ ， k ＝tan θ ＝ cos θ ＝ . ∴与此直线垂直的直线的斜率为－ ．5 4 363．答案： ( － 1,2)ax ＋ y － 4＝ 0， x ＝ 1＋ a ，由 x ＞ 0，y ＞ 0，分析：由得y ＝ 4－ 2a . x － y － 2＝0，1＋ a6得1＋ a ＞ 0 ，解得，－1＜ a ＜ 2.4－ 21＋ a ＞ 04．答案： 0°＜ α＜135°分析：由0°＜ α＜180°，∴ 0°＜ α＜135°.0°≤ α＋45°＜ 180°π 5π5．答案： [0 ， 6 ] ∪[ 6 ，π) 分析：由直线 x cos α＋ 3y ＋ 2＝ 0，因此直线的斜率为k ＝cos α－.3ββcos α3cos α33β3设直线的倾斜角为，则 tan ＝－3 ，又由于－ 3 ≤－3 ≤ 3 ，即－3 ≤tan ≤ 3 ，π5π因此 β∈[0 ， 6 ] ∪[ 6 ，π ) ．6．答案： ( －∞，－ 3] ∪[1 ，＋∞ ) 分析：由 k PA ＝－ 3，k PB ＝ 1，由图得直线l 的斜率 k 的取值范围是 ( －∞，－ 3] ∪[1 ，＋∞ ) ．1分析：∵ l 、l对于 y ＝－ x 对称，∴ l137．答案： 2的方程为－ x ＝－ 2y ＋3，即 y ＝2x ＋2，212∴l 的斜率为 12.28．答案： 4x ＋ y － 6＝ 0 或 3x ＋ 2 y － 7＝ 0 分析：直线 l 为与MN 平行或经过 MN 的中点的直线，当l 与 平行时，斜率为－ 4，故直线方程为 － 2＝－ 4( x －1) ，即 4 ＋ － 6＝ 0；当lMNyx y33经过 MN 的中点时， MN 的中点为 (3 ，－ 1) ，直线 l 的斜率为－ 2，故直线方程为 y －2＝－ 2( x－ 1) ，即 3x ＋2y － 7＝ 0.9．答案： 210 分析：分别求 P 对于直线 x ＋ y ＝ 4 及 y 轴的对称点， 为 P 1(4,2) 、P 2( － 2,0) ，由物理知识知，光芒所经行程即为 | PP | ＝2 10.1 210．答案： x ＋ 7y － 15＝ 0 或 7x － y －5＝ 0分析： (1)当斜率不存在时，直线方程为x ＝ 1，5 105 10 5与两直线交点 A (1 ，－ 3) ，B (1 ，－ 3 ) ，∴ AB ＝ － －－＝ 3≠ 2. ∴ x ＝ 1 不是所求直33线．(2) 当斜率存在时，设为k ，则所求直线的方程为 y － 2＝ k ( x － 1) ，它与两已知直线分别联立方程组，求出它与两已知直线的交点坐标分别是A ( 3k －7 －5 k ＋ 8， ) ，3k ＋ 4 3k ＋ 4( 3k － 12 8－ 10k) ．由2＝( 52＋(5k22，得＝ 7 或13k ＋ 4，4AB)3k ＋ 4 ) ＝ k k ＝－ .B 3k ＋3k ＋ 47故所求直线的方程为x ＋7 －15＝0 或 7 x － －5＝0.yy11．答案： 2x －y ＋ 8＝ 0分析：∵ l 1⊥ l 3，∴ k 1＝tan α＝2， k 2＝ tan2 α2tan α 4＝1－ tan 2α＝－3.4y ＝－ 4x － 2，l2，∴ly－ 2.3∴ ( － 3,2)∵2的纵截距为－2的方程为 ＝－由，3xx ＋ 2y － 1＝0，Pl 1过P 点，∴l 1的方程为 2x － ＋8＝0.yb 2＋ 1 1b 2＋ 112．答案： 2 分析：由两条直线垂直可得：－a ·b 2 ＝－ 1，解得 a ＝ b 2，b 2＋ 1 b 2＋ 1 111因此 ab ＝ b 2 · b ＝ b ＝ b ＋ b . 又由于 b >0，故 b ＋ b ≥2b ·b ＝ 2，1当且仅当 b ＝ b ，即 b ＝ 1 时取“＝”．|6 － 2＋3|13．答案： (7,10) 或 ( － 5，－ 2) 分析：点 C (6,2) 到直线 x －y ＋ 3＝ 0 的距离为 d ＝2＝ 7 ，由于点 A 在直线 x － ＋3＝ 0 上，能够考证点(1,4) 也在直线 x － ＋3＝ 0 上，因此设 2y B yA ( x ， y ) ．|1 －x|又由于直线 x － y ＋ 3＝ 0 的倾斜角为 45°，因此 | AB | ＝ cos45°＝2|1 － x | ，因此三角形面积117S ＝ 2| AB | d ＝ 2× 2|1 － x | · 2 ＝21. 因此 x ＝ 7 或 x ＝－ 5. 故 A 点坐标为 (7,10) 或( － 5，－ 2) ． 1 分析： l ：k ( x -2)-2 y +8=0 过定点 (2,4) 2 x 也过定点 (2,4)， 14．答案：8 ， l ： k ( y-4)=4-21 2如图， (0,4-)， (2 21224+(4-+4)212 -+8. 当1获得最小k+2,0) ， =kk =4kk = 时，SAB kS 22k 8值 .二、解答题：15．解： (1) 法一：当 sin θ＝ 0 时， l1的斜率不存在， l 2 的斜率为零， l 1 明显不平行于 l 2.当 sinθ ≠0时，1＝－ 1 ， k 2＝－ 2sinθ ，欲使 l 1∥ 2，只需－ 1 ＝－ 2sin θ ， sin θk sin θ lsin θ2＝± 2，∴ θ＝k π± π， k ∈Z ，此时两直线截距不相等．∴当θ＝ k π± π， k ∈Z 时， l 1∥l 2.442212法二：由 A 1B 2－ A 2B 1＝0，即 2sin θ－ 1＝ 0，得 sin θ＝2，∴ sin θ＝± 2 ，由 B 1C 2－ B 2C 1≠0，即 1＋ sin ≠0，即 sin ≠－ 1，得 ＝ π ＝ k π± π l 1∥ l 2.θ θ θ k 4 k θ k4(2) ∵ l 1 ⊥l 2 ∴A 1A 2＋ B 1B 2＝ 0，∴ 2sin θ＋sin θ＝ 0，即 sin θ ＝ 0，∴ θ＝ k π(k ∈Z) ，∴当 θ＝ k π， k ∈Z 时， l 1⊥ l 2.16．解：（ 1）设直线 l 的方程为 y 1 x b ，则直线 l 与坐标轴的交点为 A( 6b,0) 、 B(0, b)依题设有 1|6b |6 1|b | 3 ，得 b1 ，则直线 l 的方程为 y x1263 4 13a3 （ 2）设直线 l 的方程为x ya ba1，则由，解得ab12 或23b4 b| ab |2则直线 l 方程为x y 1 或 xy 1即 24 x 3y 120 或 2x 3 y 634 3 2217．解： (1) 若 l1，l 2， l 3 三条直线交于一点．明显 m ≠4，若 m ＝ 4，则 l 1∥ l 2.4x ＋ y － 4＝0，得 l 1， l 2 的交点坐标为 (4－ 4m由， ) ．＋ ＝ 04－ m 4－ mmx y代入l 3的方程得 8· －4m2－ 3 － 4＝0. 解得＝－1或 ＝，4－m m 4－ mmm32∴当 m ＝－ 1 或 m ＝ 3时， l 1，l 2，l 3 交于一点．1(2) 若 l 1 ∥l 2，则 m ＝4，若 l 1∥l 3，则 m ＝－ 6，若 l 2∥l 3，则 m ∈?.(3) 若 l 1 ∥l 2∥ l 3，则 m ∈ ?.21综上知：当 m ＝－ 1 或 m ＝3或 m ＝ 4 或 m ＝－ 6时，三条直线不可以组成三角形，即组成三角形的条件是1 12 2m ∈( －∞，－ 1) ∪( － 1，－ ) ∪( －， )∪( ，4)∪(4，＋∞)．663311| a ＋ 2|7 518．解： (1) ∵ l 2 ：2x － y － 2＝ 0，∴ l 1 与 l 2 的距离 d ＝5＝ 10 ，∵ a ＞ 0，∴ a ＝ 3.(2) 设存在点 P ( x 0， y 0) 知足②，则 P 点在与 l 1、 l 2 平行的直线 l ′： 2x － y ＋c ＝ 0 上，1| c － 3| 1 | c ＋ 2|13 111311且5 ＝ 2· 5 ，即 c ＝ 2 或 c ＝6 ，∴2x 0－ y 0＋ 2 ＝ 0 或 2x 0 －y 0＋ 6 ＝ 0，若 P 点知足条件③，由点到直线的距离公式有：|2 x 0 － y 0 ＋3| ＝2| x 0 ＋y 0－ 1| ，55 2即|2 x 0－ y 0＋ 3| ＝ | x 0＋ y 0－1|. ∴ x 0－ 2y 0 ＋4＝ 0 或 3x 0＋ 2＝ 0， ∵P 在第一象限，∴3 x 0 ＋2＝ 0 不行能，13x 0＝－ 3，11 2x 0－ y 0＋ ＝ 0，1(舍去)2x 0－ y 0＋ ＝ 0， 联立 2解得由 6x 0－ 2y 0＋ 4＝ 0.y 0＝ 2.x 0－ 2 0＋ 4＝ 0，y11 37x ＝ 9，得∴P ( 9， 18) 即为同时知足条件的点．y 0＝ 37，1819．解： (1)证明：直线 l 的方程是： k ( x ＋2) ＋ (1 － y ) ＝ 0，x ＋ 2＝0x ＝－ 2 令解之得y ＝ 1，1－ y ＝0∴不论 k 取何值，直线总经过定点 ( － 2,1) ．(2) 由方程知，当k ≠0时直线在 x 轴上的截距为－1＋ 2k，k－1＋2k≤－ 2 在 y 轴上的截距为1＋2k ，要使直线不经过第四象限，则一定有k，1＋2k ≥1解之得 k ＞ 0；当 k ＝ 0 时，直线为y ＝ 1，合题意，故 ≥0.k1＋ 2k1＋ 2k (3) 由 l 的方程，得 A －－ k ＜ 0，， 0 ， B(0,1 ＋ 2k) ．依题意得，解得 kk1＋2k ＞ 0＞ 0.11 1＋ 2k1(1 ＋2k) 2 1 1 1∵S ＝ 2·|OA| ·|OB| ＝ 2·k·|1 ＋ 2k| ＝ 2·k＝ 2 4k ＋ k ＋4 ≥ 2(2 ×2＋ 4)＝ 4，“＝”建立的条件是k ＞0且 41 k 1＝ ，即 ＝ ，k k 2∴S min ＝4，此时 l ： x － 2y ＋4＝ 0．20．解： (1)由图知 A(1,1), B(1,0) ， k OP1, k BP 1 ,22设直线 MN 的斜率为 k ，直线 MN 与POB 不可以订交，因此1≤ k ≤ 1，22（ 2）直线 MN 的方程为 y1 k( x 1) ，令 x 1 得 y 2k 1 N (1, 2k 1 )4 2 44 令 y x 得 x y2k 1M ( 2k 1 , 2k 1 )4( k 1)4(k 1) 4(k 1)uuur1 uuur1 2k1 1 2k 111 2k1 1 ) ∴ k 1∵ MPPN ，∴(4(k,44(k )(1,442321) 1) 32∴ MN 的方程为 x2 y 1 0 ，此时和 BP 重合．（ 3）由（ 2）知 | AN |2k 13 2 k12k 12k 3 144, 点 M 到直线 AN 的距离为4(k 1)4 (k 1)S AMN 1 3 2k 2k 3 1[(1 k) 1 1]244(k 1) 8 4(1 k)Q1≤ k ≤11≤ 1 k ≤ 3而函数 yx1 在[1, ) 上是增函数，故当22 224x 21k3,即 k1 时 S AMN 获得最大值1当 1 k1 ,即 k1时，22322S AMN 获得最小值1（最小值也可用基本不等式直接获得）.4。

高二数学暑假自主学习单元检测九直线与圆一、填空题：本大题共14 题，每小题 5 分，共70 分．1．与直线 x＋ 3y－ 1＝ 0 垂直的直线的倾斜角为．2．过点 (2,1) 且在两坐标轴截距相等的直线方程是．3．直线 3x－ y＋ m＝ 0 与圆 x2＋ y2－2x－ 2＝ 0 相切，则实数m＝．4．已知实数 x，y 满足2x＋ y＋ 5＝0，那么 x2＋ y2的最小值为．5．已知直线l1 ax 3 y 1 0 l2 2x (a 1)y 1 0，若l1∥l 2，则实数 a 的值是．：，：6．已知直线l1 ：axy2a 1 0 和 l2： 2x (a 1) y 20 ( aR)，则l1l2 的充要条件是a ．7．已知直线 3x+2y-3=0 和 6x+my+1=0 互相平行，则它们之间的距离是．8．已知圆 x2 y2 m 与圆 x2 y2 6x 8 y 11 0相交，则实数m的取值范围为．9．若圆心在x 轴上、半径为5的圆 C 位于 y 轴左侧，且与直线x＋ 2y＝0 相切，则圆 C 的方程是．10．在平面直角坐标系xOy 中，已知圆x2＋ y2＝ 4 上有且仅有四个点到直线12x －5y＋ c＝0 的距离为 1，则实数 c 的取值范围是．11．过原点O作圆 x2+y2-－ 6x－8y＋ 20=0 的两条切线，设切点分别为P、 Q，则线段 PQ的长为．12．直线 y＝ kx ＋ 3 与圆 (x － 2) 2＋ (y － 3) 2＝ 4 相交于 M，N 两点，若 |MN|≥23，则实数 k 的取值范围是．13．若直线y＝ x＋ b 与曲线 y＝ 3－4x－ x2有公共点，则 b 的取值范围是．14．已知AC、 BD 为圆 O :x2y2 4 的两条相互垂直的弦，垂足为M 1, 2, 则四边形ABCD 的面积的最大值为．二、解答题：本大题共 6 小题，共90 分，解答应写出文字说明、证明过程或演算步骤．15． ( 本小题满分14 分 )已知圆 C 过点 (1,0)，且圆心在x 轴的正半轴上，直线l：y＝ x－ 1 被圆 C 所截得的弦长为2 2 ，求过圆心且与直线l 垂直的直线的方程．16． ( 本小题满分14 分)自点 A(-3,3) 发出的光线 l 射到 x 轴上,被 x 轴反射, 其反射光线所在的直线与圆x2 y2 4 x 4y 7 0相切, 求光线 l 所在的直线方程．17． ( 本小题满分14 分 )已知直线 l 过点 P 3,2 ，且与x轴、y轴的正半轴分别交于A B两点．、（ 1）求ABO的面积的最小值及其这时的直线l 的方程。

2012届高三模拟考试试卷(五)南通市2012届高三第一次调研测试数 学(满分160分，考试时间120分钟)2012．3参考公式：样本数据x 1，x 2，…，x n 的方差s 2＝1n (x i －x －)2，其中x －＝1n x i .一、 填空题：本大题共14小题，每小题5分，共70分．1. 在平面直角坐标系xOy 中，双曲线y 2－x 2＝1的离率心为____________．2. 若复数z 满足(1＋2i)z ＝－3＋4i(i 是虚数单位)，则z ＝____________.3. 在右图的算法中，最后输出的a 、b 的值依次是____________． a←1b←2c←3c←a a←b b←cPrint a ，b(第3题)4. 一组数据9.8,9.9,10，a,10.2的平均数为10，则该组数据的方差为______________．5. 设全集U ＝Z ，集合A ＝{x|x 2－x －2≥0，x ∈Z }，则U A ＝____________(用列举法表示)．6. 在平面直角坐标系xOy 中，已知向量a ＝(1,2)，a －12b ＝(3,1)，则a·b ＝____________. 7. 将甲、乙两个球随机放入编号为1、2、3的3个盒子中，每个盒子的放球数量不限，则在1、2号盒子中各有1个球的概率为____________．8. 设P 是函数y ＝x(x ＋1)图象上异于原点的动点，且该图象在点P 处的切线的倾斜角为θ，则θ的取值范围是____________．9. 如图，矩形ABCD 的三个顶点A 、B 、C 分别在函数y ＝log 22x ，y ＝x 12，y ＝⎝ ⎛⎭⎪⎫22x 的图象上，且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2，则点D 的坐标为__________．(第9题)10. 观察下列等式： 13＝1， 13＋23＝9，13＋23＋33＝36，13＋23＋33＋43＝100， …猜想：13＋23＋33＋43＋…＋n 3＝____________(n ∈N *)．11. 在棱长为4的正方体ABCDA 1B 1C 1D 1中，E 、F 分别为棱AA 1、D 1C 1上的动点，点G 为正方形B 1BCC 1的中心．则空间四边形AEFG 在该正方体各个面上的正投影所构成的图形中，面积的最大值为____________．12. 若a 1x≤sinx≤a 2x 对任意的x ∈⎣⎡⎦⎤0，π2都成立，则a 2－a 1的最小值为____________．13. 如图，在平面直角坐标系xOy 中，F 1，F 2分别为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点，B 、C 分别为椭圆的上、下顶点，直线BF 2与椭圆的另一交点为D.若cos ∠F 1BF 2＝725，则直线CD 的斜率为__________．(第13题)14. 各项均为正偶数的数列a 1，a 2，a 3，a 4中，前三项依次成公差为d(d ＞0)的等差数列，后三项依次成公比为q 的等比数列．若a 4－a 1＝88，则q 的所有可能的值构成的集合为____________．二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分)在斜三角形ABC 中，角A 、B 、C 的对边分别为a 、b 、c.(1) 若2sinAcosC ＝sinB ，求ac 的值； (2) 若sin(2A ＋B)＝3sinB ，求tanAtanC 的值．16.(本小题满分14分)如图，在六面体ABCDA 1B 1C 1D 1中，AA 1∥CC 1，A 1B ＝A 1D ，AB ＝AD.求证： (1) AA 1⊥BD ；(2) BB 1∥DD 1.将52名志愿者分成A 、B 两组参加义务植树活动，A 组种植150捆白杨树苗，B 组种植200捆沙棘树苗．假定A 、B 两组同时开始种植．(1) 根据历年统计，每名志愿者种植一捆白杨树苗用时25小时，种植一捆沙棘树苗用时12小时．应如何分配A 、B 两组的人数，使植树活动持续时间最短？(2) 在按(1)分配的人数种植1小时后发现，每名志愿者种植一捆白杨树苗仍用时25小时，而每名志愿者种植一捆沙棘树苗实际用时23小时，于是从A 组抽调6名志愿者加入B 组继续种植，求植树活动所持续的时间．如图，在平面直角坐标系xOy 中，已知圆C 1：(x ＋1)2＋y 2＝1，圆C 2：(x －3)2＋(y －4)2＝1.(1) 若过点C 1(－1,0)的直线l 被圆C 2截得的弦长为65，求直线l 的方程； (2) 设动圆C 同时平分圆C 1的周长、圆C 2的周长． ① 证明：动圆圆心C 在一条定直线上运动；② 动圆C 是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．已知函数f(x)＝x ＋sinx.(1) 设P 、Q 是函数f(x)图象上相异的两点，证明：直线PQ 的斜率大于0；(2) 求实数a 的取值范围，使不等式f(x)≥axcosx 在⎣⎡⎦⎤0，π2上恒成立．设数列{a n}的各项均为正数．若对任意的n∈N*，存在k∈N*，使得a2n＋k＝a n·a n＋2k成立，则称数列{a n}为“J k型”数列．(1) 若数列{a n}是“J2型”数列，且a2＝8，a8＝1，求a2n；(2) 若数列{a n}既是“J3型”数列，又是“J4型”数列，证明：数列{a n}是等比数列．2012届高三模拟考试试卷(五)数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A 、B 、C 、D 四小题中选做2题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修41：几何证明选讲) 如图，AB 是半圆O 的直径，延长AB 到C ，使BC ＝3，CD 切半圆O 于点D ，DE ⊥AB ，垂足为E.若AE ∶EB ＝3∶1，求DE 的长．B. (选修42：矩阵与变换)在平面直角坐标系xOy 中，直线y ＝kx 在矩阵⎣⎢⎡⎦⎥⎤0 11 0对应的变换下得到的直线过点P(4,1)，求实数k 的值．C. (选修44：坐标系与参数方程)在极坐标系中，已知圆ρ＝asinθ(a ＞0)与直线ρcos ⎝⎛⎭⎫θ＋π4＝1相切，求实数a 的值．D. (选修45：不等式选讲)已知正数a ，b ，c 满足abc ＝1，求证：(a ＋2)(b ＋2)(c ＋2)≥27.【必做题】 第22题、第23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．22. 已知数列{a n }满足：a 1＝12，a n ＋1＝2a na n ＋1(n ∈N *)．(1) 求a 2，a 3的值；(2) 证明：不等式0＜a n ＜a n ＋1对于任意n ∈N *都成立．23.如图，在平面直角坐标系xOy中，抛物线的顶点在原点，焦点为F(1,0)．过抛物线在x轴上方的不同两点A、B作抛物线的切线AC、BD，与x轴分别交于C、D两点，且AC与BD交于点M，直线AD与直线BC交于点N.(1) 求抛物线的标准方程；(2) 求证：MN⊥x轴；(3) 若直线MN与x轴的交点恰为F(1,0)，求证：直线AB过定点．2012届高三模拟考试试卷(五)(南通)数学参考答案及评分标准1. 22. 1＋2i3. 2,14. 0.025. {0,1}6. 07. 298. ⎣⎡⎭⎫π3，π29. ⎝⎛⎭⎫12，1410.⎣⎡⎦⎤n n ＋122 11. 12 12. 1－2π 13. 1225 14. ⎩⎨⎧⎭⎬⎫53，8715. 解：(1) 由正弦定理，得sinA sinB ＝ab ， 从而2sinAcosC ＝sinB 可化为2acosC ＝b ，(3分) 由余弦定理，得2a×a 2＋b 2－c 22ab ＝b ， 整理得a ＝c ，即ac ＝1.(7分)(2) 在斜三角形ABC 中，A ＋B ＋C ＝π，所以sin(2A ＋B)＝3sinB 可化为sin[π＋(A －C)]＝3sin[π－(A ＋C)]， 即－sin(A －C)＝3sin(A ＋C)，(10分)故－sinAcosC ＋cosAsinC ＝3(sinAcosC ＋cosAsinC)， 整理，得4sinAcosC ＝－2cosAsinC ，(12分)因为△ABC 是斜三角形，所以sinAcosAcosC≠0， 所以tanA tanC ＝－12.(14分)16. 证明：(1) 取线段BD 的中点M ，连结AM 、A 1M ，因为A 1D ＝A 1B ，AD ＝AB ，所以BD ⊥AM ，BD ⊥A 1M ，(3分)又AM∩A 1M ＝M ，AM 、A 1M 平面A 1AM ，所以BD ⊥平面A 1AM ， 而AA 1平面A 1AM ， 所以AA 1⊥BD.(7分) (2) 因为AA 1∥CC 1，AA 1平面D 1DCC 1，CC 1平面D 1DCC 1， 所以AA 1∥平面D 1DCC 1.(9分)又AA 1平面A 1ADD 1，平面A 1ADD 1∩平面D 1DCC 1＝DD 1，(11分) 所以AA 1∥DD 1，同理得AA 1∥BB 1， 所以BB 1∥DD 1.(14分)17. 解：(1)设A 组人数为x ，且0＜x ＜52，x ∈N *， 则A 组活动所需时间f(x)＝150×25x ＝60x ，(2分) B 组活动所需时间g(x)＝200×1252－x ＝10052－x ，(4分)令f(x)＝g(x)，即60x ＝10052－x，解得x ＝392，所以两组同时开始的植树活动所需时间F(x)＝⎩⎨⎧60x ，x≤19，x ∈N *，10052－x ，x≥20，x ∈N *，(6分)而F(19)＝6019，F(20)＝258，故F(19)＞F(20)，所以当A 、B 两组人数分别为20、32时，使植树活动持续时间最短．(8分) (2) A 组所需时间为1＋150×25－20×120－6＝367(小时)，(10分)B 组所需时间为1＋200×23－32×132＋6＝323(小时)，(12分)所以植树活动所持续的时间为367小时．(14分)18. 解：(1) 设直线l 的方程为y ＝k(x ＋1)，即kx －y ＋k ＝0，因为直线l 被圆C 2截得的弦长为65，而圆C 2的半径为1，所以圆心C 2(3,4)到l ：kx －y ＋k ＝0的距离为|4k －4|k 2＋1＝45.(3分)化简，得12k 2－25k ＋12＝0，解得k ＝43或k ＝34， 所以直线l 的方程为4x －3y ＋4＝0或3x －4y ＋3＝0.(6分) (2) ① 证明：设圆心C(x ，y)，由题意，得CC 1＝CC 2， 即x ＋12＋y 2＝x －32＋y －42， 化简得x ＋y －3＝0，即动圆圆心C 在定直线x ＋y －3＝0上运动．(10分) ② 圆C 过定点，设C(m,3－m)，则动圆C 的半径为1＋CC 21＝1＋m ＋12＋3－m 2， 于是动圆C 的方程为(x －m)2＋(y －3＋m)2＝1＋(m ＋1)2＋(3－m)2， 整理，得x 2＋y 2－6y －2－2m(x －y ＋1)＝0，(14分)由⎩⎪⎨⎪⎧x －y ＋1＝0，x 2＋y 2－6y －2＝0，得⎩⎨⎧x ＝1＋322，y ＝2＋322；或⎩⎨⎧x ＝1－322，y ＝2－322.所以定点的坐标为⎝⎛⎭⎫1－322，2－322，⎝⎛⎭⎫1＋322，2＋322.(16分)19. (1) 证明：由题意，得f′(x)＝1＋cosx≥0，所以函数f(x)＝x ＋sinx 在R 上单调递增，设P(x 1，y 1)，Q(x 2，y 2)，则有y 1－y 2x 1－x 2＞0，即k PQ ＞0.(6分) (2) 解：当a≤0时，f(x)＝x ＋sinx≥0≥axcosx 恒成立．(8分)当a ＞0时，令g(x)＝f(x)－axcosx ＝x ＋sinx －axcosx ，g′(x)＝1＋cosx －a(cosx －xsinx)＝1＋(1－a)cosx ＋axsinx.① 当1－a≥0，即0＜a≤1时，g′(x)＝1＋(1－a)cosx ＋axsinx ＞0，所以g(x)在⎣⎡⎦⎤0，π2上为单调增函数， 所以g(x)≥g(0)＝0＋sin0－a×0×cos0＝0，符合题意．(10分)② 当1－a ＜0，即a ＞1时，令h(x)＝g′(x)＝1＋(1－a)cosx ＋axsinx ，于是h′(x)＝(2a －1)sinx ＋axcosx ，因为a ＞1，所以2a －1＞0，从而h′(x)≥0，所以h(x)在⎣⎡⎦⎤0，π2上为单调增函数， 所以h(0)≤h(x)≤h ⎝⎛⎭⎫π2，即2－a≤h(x)≤π2a ＋1， 亦即2－a≤g′(x)≤π2a ＋1.(12分)(ⅰ) 当2－a≥0，即1＜a≤2时，g′(x)≥0，所以g(x)在⎣⎡⎦⎤0，π2上为单调增函数．于是g(x)≥g(0)＝0，符合题意．(14分) (ⅱ) 当2－a ＜0，即a ＞2时，存在x 0∈⎝⎛⎭⎫0，π2，使得 当x ∈(0，x 0)时，有g′(x)＜0，此时g(x)在(0，x 0)上为单调减函数，从而g(x)＜g(0)＝0，不能使g(x)＞0恒成立，综上所述，实数a 的取值范围为a≤2.(16分)20. (1) 解：由题意，得a 2，a 4，a 6，a 8，…成等比数列，且公比q ＝⎝⎛⎭⎫a 8a 213＝12， 所以a 2n ＝a 2q n －1＝⎝⎛⎭⎫12n －4.(4分) (2) 证明：由{a n }是“J 4 型”数列，得a 1，a 5，a 9，a 13，a 17，a 21，…成等比数列，设公比为t ，(6分)由{a n }是“J 3型”数列，得a 1，a 4，a 7，a 10，a 13，…成等比数列，设公比为α1；a 2，a 5，a 8，a 11，a 14，…成等比数列，设公比为α2；a 3，a 6，a 9，a 12，a 15，…成等比数列，设公比为α3；则a 13a 1＝α41＝t 3，a 17a 5＝α42＝t 3，a 21a 9＝α43＝t 3， 所以α1＝α2＝α3，不妨记α＝α1＝α2＝α3，且t ＝α43，(12分)于是a 3k －2＝a 1αk －1＝a 1(3α)(3k －2)－1，a3k－1＝a5αk－2＝a1tαk－2＝a1αk－23＝a1(3α)(3k－1)－1，a3k＝a9αk－3＝a1t2αk－3＝a1αk－13＝a1(3α)3k－1，所以a n＝a1(3α)n－1，故{a n}为等比数列．(16分)2012届高三模拟考试试卷(五)(南通) 数学附加题参考答案及评分标准 21. A. 选修41：几何证明选讲解：连结AD 、DO 、DB.由AE ∶EB ＝3∶1，得DO ∶OE ＝2∶1.又DE ⊥AB ，所以∠DOE ＝60°.故△ODB 为正三角形．(5分)于是∠DAC ＝30°＝∠BDC.而∠ABD ＝60°，故∠C ＝30°＝∠BDC.所以DB ＝BC ＝ 3.在△OBD 中，DE ＝32DB ＝32.(10分)B. 选修42：矩阵与变换解：设变换T ：⎣⎢⎡⎦⎥⎤x y ―→⎣⎢⎡⎦⎥⎤x′y′，则⎣⎢⎡⎦⎥⎤x′y′＝⎣⎢⎡⎦⎥⎤0 110⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤y x ，即⎩⎪⎨⎪⎧ x′＝y ，y′＝x.(5分) 代入直线y ＝kx ，得x′＝ky′.将点P(4,1)代入上式，得k ＝4.(10分)C. 选修44：坐标系与参数方程解：将圆ρ＝asinθ化成普通方程为x 2＋y 2＝ay ，整理，得x 2＋⎝⎛⎭⎫y －a 22＝a 24. 将直线ρcos ⎝⎛⎭⎫θ＋π4＝1化成普通方程为x －y －2＝0.(6分) 由题意，得⎪⎪⎪⎪－a 2－22＝a2.解得a ＝4＋2 2.(10分)D. 选修45：不等式选讲证明：(a ＋2)(b ＋2)(c ＋2)＝(a ＋1＋1)(b ＋1＋1)(c ＋1＋1)(4分)≥3·3a·3·3b·3·3c＝27·3abc＝27(当且仅当a ＝b ＝c ＝1时等号成立)．(10分)22. (1) 解：由题意，得a 2＝23，a 3＝45.(2分)(2) 证明：① 当n ＝1时，由(1)，知0＜a 1＜a 2，不等式成立．(4分)② 设当n ＝k(k ∈N *)时，0＜a k ＜a k ＋1成立，(6分)则当n ＝k ＋1时，由归纳假设，知a k ＋1＞0.而a k ＋2－a k ＋1＝2a k ＋1a k ＋1＋1－2a k a k ＋1＝2a k ＋1a k ＋1－2a k a k ＋1＋1a k ＋1＋1a k ＋1＝2a k ＋1－a k a k ＋1＋1a k ＋1＞0， 所以0＜a k ＋1＜a k ＋2，即当n ＝k ＋1时，不等式成立．由①②，得不等式0＜a n ＜a n ＋1对于任意n ∈N *成立．(10分)23. 解：(1) 设抛物线的标准方程为y 2＝2px(p ＞0)，由题意，得p 2＝1，即p ＝2.所以抛物线的标准方程为y 2＝4x.(3分)(2) 设A(x 1，y 1)，B(x 2，y 2)，且y 1＞0，y 2＞0.由y 2＝4x(y ＞0)，得y ＝2x ，所以y′＝1x. 所以切线AC 的方程为y －y 1＝1x 1(x －x 1)，即y －y 1＝2y 1(x －x 1)． 整理，得yy 1＝2(x ＋x 1)， ①且C 点坐标为(－x 1,0)．同理得切线BD 的方程为yy 2＝2(x ＋x 2)， ②且D 点坐标为(－x 2,0)．由①②消去y ，得x M ＝x 1y 2－x 2y 1y 1－y 2.(5分) 又直线AD 的方程为y ＝y 1x 1＋x 2(x ＋x 2)， ③ 直线BC 的方程为y ＝y 2x 1＋x 2(x ＋x 1)． ④ 由③④消去y ，得x N ＝x 1y 2－x 2y 1y 1－y 2. 所以x M ＝x N ，即MN ⊥x 轴．(7分)(3) 由题意，设M(1，y 0)，代入(1)中的①②，得y 0y 1＝2(1＋x 1)，y 0y 2＝2(1＋x 2)， 所以A(x 1，y 1)，B(x 2，y 2)都满足方程y 0y ＝2(1＋x)．所以直线AB 的方程为y 0y ＝2(1＋x)．故直线AB 过定点(－1,0)．(10分)你脸上云淡风轻，谁也不知道你牙咬得多紧。

江苏省南通中学2023-2024学年第一学期12月阶段考试高一数学一、单选题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}20,1,A a =，{}1,0,23B a =+，若A B =，则a 等于（）A ．1-或3B ．0或1-C ．3D ．1-2．若扇形的弧长是8，面积是16，则这个扇形的圆心角的弧度数是（）A ．2B ．3C ．4D ．53．已知 1.21.2a =， 1.20.6b =，ln 0.6c =，则,,a b c 的大小为（）A ．a c b >>B ．a b c >>C ．b c a>>D ．b a c>>4．“2x >”是“|1|1x ->”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．已知35,37a b ==，则9a b -=（）A ．57B ．75C ．4925D ．25496．函数()2cos ln2cos xf x x x-=+的部分图象可能是()A ．B ．C ．D ．7．设()f x 是定义域为R 且最小正周期为2π的函数，且有sin ,0π()cos ,π0x x f x x x ≤≤⎧=⎨-<<⎩，则13π()4f -=（）A 2B ．2C ．0D ．18．在平面直角坐标系xOy 中，点()12ππcos ,sin ,cos ,sin 33P P αααα⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，3ππcos ,sin 66P αα⎛⎫⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭⎝⎭，则下列说法错误的是（）A ．线段2OP 与3OP 的长均为1B ．线段23P P 的长为1C ．当π3α=时，点12,P P 关于y 轴对称D ．当13π12α=时，点13,P P 关于x 轴对称二、多选题：本大题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．下列结论正确的是（）A ．()cos πcos αα-=B ．πsin cos 2αα⎛⎫-=- ⎪⎝⎭C ．()tan πtan αα--=-D ．5πcos sin 2αα⎛⎫+= ⎪⎝⎭10．已知M ，N 为全集U 的真子集，若()U M N ⋂=∅ð，则（）A ．M N ⋂=∅B ．M N M ⋃=C ．()U N M =∅ðD ．()U N M U= ð11．已知函数()f x ，当[1,1]x ∈-时单调递增，若角A ，B ，C 是锐角三角形的内角，则下列说法正确的是（）A ．(sin )(cos )f A fB >；B ．(sin )(cos )f A f B <C ．(cos )(sin )f A f B >；D ．(cos )(sin )f A f B <12．定义在R 上的函数()f x 满足()()2f x f x =+，当[]3,5x ∈时，()24f x x =--，则下列说法正确的是（）A ．()f x 为偶函数B ．()f x 的图象没有对称中心C ．()f x 的增区间为[]()21,22Z k k k ++∈D ．方程()ln 0f x x -=有5个实数解三、填空题：本大题共4小题，每小题5分，共20分.13．已知关于x 的不等式220ax bx ++<的解集为122x x ⎧⎫<<⎨⎬⎩⎭，则a b +=.14．为了保证信息安全传输，有一种系统称为秘密密钥密码系统，其加密、解密原理如下：明文−−−−−→加密密钥系统密文t −−−→发送密文t −−−−−→解密密钥系统明文y ．现在加密密钥为幂函数，解密密钥为指数函数．过程如下：发送方发送明文“9”，通过加密后得到密文“3”，再发送密文“3”，接受方通过解密密钥得到明文“27”．若接受方得到明文“9”，则发送方发送的明文为．15．已知cos 6απ⎛⎫-= ⎪⎝⎭54cos sin 63ππαα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭的值为．16．定义{},min ,,a a b a b b a b≤⎧=⎨>⎩若函数(){}2min 33,33f x x x x =-+--+，则()f x 的最大值为；若()f x 在区间[],m n 上的值域为3,24⎡⎤⎢⎥⎣⎦，则n m -的最大值为．四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．已知全集为R ，集合{}12A x x =≤≤，{B x x m =<或}21,0x m m >+>.(1)当2m =时，求A B ⋂；(2)若R A B ⊆ð，求实数m 的取值范围.18．已知3,24παπ⎛⎫∈ ⎪⎝⎭,且sin cos αα-=(1)求1tan tan αα+的值;(2)求()()()cos 2cos 2sin cos 2πααπαπα⎛⎫--+ ⎪⎝⎭--+-的值.19．已知函数()2sin 3cos 3f x x x =--+，x R ∈．（1）求()f x 的值域；（2）求不等式()75cos 22f x x ≥-+的解集．20．习近平指出，倡导环保意识、生态意识，构建全社会共同参与的环境治理体系，让生态环保思想成为社会生活中的主流文化.某化工企业探索改良工艺，使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为32mg/m ，首次改良后所排放的废气中含有的污染数量为31.94mg/m .设改良工艺前所排放的废气中含有的污染物数量为0r ，首次改良工艺后所排放的废气中含有的污染物数量为1r ，则第n 次改良后所排放的废气中的污染物数量n r ，可由函数模型()0.50015n pn r r r r +=--⋅（p ∈R ，*n ∈N ）给出，其中n 是指改良工艺的次数.(1)试求改良后n r 的函数模型；(2)依据国家环保要求，企业所排放的废气中含有的污染物数量不能超过30.08mg/m .试问：至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标？（参考数据：取lg 20.3=）21．已知函数()1221x x f x -=+.(1)求()()22f f -+的值；(2)求函数()f x 的值域；(3)若()()24221x a g x f x a ⎡⎤=-+⎣⎦+，且对任意的1x 、2x ∈R ，都有()()123g x g x -<，求实数a 的取值范围.22．已知函数()()2log 41xf x kx =++为偶函数．(1)求实数k 的值；(2)解关于m 的不等式()()211f m f m +>-；(3)设()()()2log 20xg x a a a =⋅+≠，若函数()f x 与()g x 图象有2个公共点，求实数a 的取值范围．1．C【分析】依题意可得223a a =+，求出a 的值，再检验即可.【详解】因为{}20,1,A a =，{}1,0,23B a =+且A B =，即223a a =+，解得1a =-或3a =，当1a =-时2231a a =+=，不满足集合元素的互异性，故舍去，当3a =时{}0,1,9A =，{}1,0,9B =，符合题意.故选：C 2．A【分析】利用扇形的面积、弧长公式求圆心角的弧度即可.【详解】令扇形的圆心角的弧度数为θ，半径为r ，则18162r ⨯=，即4r =，又8r θ=，故2θ=.故选：A 3．B【分析】根据指数函数和对数函数的图像及单调性解题即可.【详解】根据指数函数的图像及性质可知：1a >，0x >，所以函数x y a =单调递增且01x a a >=，故 1.21.21a =>，又根据指数函数的图像及性质可知：1a <，0x >，所以函数x y a =单调递减且01x a a <=，故 1.20.61b =<，又根据对数函数的图像及性质可知：函数ln y x =单调递增，则当1x <时，ln ln10y x =<=，故ln 0.60c =<，综上：10a b c >>>>，故选：B.【点睛】对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．当底数与指数都不相同时，选取适当的“媒介”数（通常以“0”或“1”为媒介），分别与要比较的数比较，从而可间接地比较出要比较的数的大小．4．A【分析】根据充分条件、必要条件的定义判断即可.【详解】由|1|1x ->，则11x ->或11x -<-，解得2x >或0x <，所以由2x >推得出|1|1x ->，即充分性成立，由|1|1x ->推不出2x >，即必要性不成立，所以“2x >”是“|1|1x ->”的充分不必要条件.故选：A 5．D【分析】根据指数幂及对数的运算性质计算.【详解】∵35,37a b ==，∴33log 5,log 7a b ==，∴223333325222log 52log 7log 5log 7log 49a b -=-=-=，∴3o 225l g 4922549933a ba b--===.故选：D.6．C【分析】先确定函数奇偶性，再确定0x →的时候y 的值.【详解】因为()()()()()2cos 2cos ln ln2cos 2cos x xf x x x f x x x----=-=-=-+-+，所以()f x 为奇函数，排除AB ；又0x +→时2cos 1ln ln 02cos 3x x -→<+，所以排除D,故选：C 7．A【分析】利用给定函数的性质，结合分段函数解析式代入计算作答.【详解】因为()f x 是定义域为R 且最小正周期为2π的函数，且sin ,0π()cos ,π0x x f x x x ≤≤⎧=⎨-<<⎩，所以13π3π3π3π()(4π)()sin 44442f f f -=-===.故选：A8．B【分析】结合同角三角函数的平方关系，计算线段2OP 与3OP 的长，判断A ；利用两点间距离公式结合两角差的余弦公式，可判断B ；根据三角函数特殊值求出12,P P 坐标，判断C ；结合诱导公式化简可得13,P P 坐标，判断D.【详解】对于A ，21OP =,31OP =，则线段2OP 与3OP 的长均为1，A 说法正确；对于B ，23P P ==B 说法错误；对于C ，当π3α=时，1ππcos ,sin 33P ⎛⎫⎪⎝⎭，即112P ⎛ ⎝⎭，22π2πcos ,sin33P ⎛⎫ ⎪⎝⎭，即212P ⎛- ⎝⎭，故点12,P P 关于y 轴对称，C 说法正确；对于D ，当13π12α=时，113π13πcos ,sin 1212P ⎛⎫ ⎪⎝⎭，即1ππcos ,sin 1212P⎛⎫-- ⎪⎝⎭313ππ13ππcos ,sin 126126P ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即3ππcos ,sin 1212P ⎛⎫- ⎪⎝⎭，则点13,P P 关于x 轴对称，D 说法正确，即说法错误的是B ，故选：B 9．BC【分析】根据三角函数诱导公式一一化简各选项中的三角函数式，判断正误，即可得答案.【详解】对于A ，()()cos πcos πcos ααα-=-=-，A 错误；对于B ，ππsin sin cos 22ααα⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭，B 正确；对于C ，()()tan πtan πtan ααα--=-+=-，C 正确；对于D ，5πππcos cos 2π=cos sin 222αααα⎛⎫⎛⎫⎛⎫+=+++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，D 错误，故选：BC 10．BD【分析】依题意可得N M ⊆，即可判断A 、B 、D ，分N M =和N M 两种情况判断C.【详解】因为M ，N 为全集U 的真子集且()U M N ⋂=∅ð，所以N M ⊆，则M N N ⋂=，M N M ⋃=，()U N M U = ð，故A 错误，B 、D 正确；当N M =时()U N M =∅ ð，当N M 时()U N M ≠∅ ð，故C 错误；故选：BD 11．AD【分析】根据正弦函数的单调性及()f x 的单调性比较可得．【详解】由题意π2A B +>，且π02A <<，π02B <<，因此ππ022B A <-<<，∴πcos sin()sin 2B B A =-<，而()f x 在[1,1]-上递增，sin ,cos [1,1]A B ∈-，∴(cos )(sin )f B f A <，同理(cos )(sin )f A f B <，故选：AD ．12．ACD【分析】由题意可判断函数的周期，结合[]3,5x ∈时的解析式，即可作出函数图象，数形结合，即可判断A ，B ，C ；将方程()ln 0f x x -=的解的个数问题，转化为函数知ln y x =和()f x 的图象的交点个数问题，即可判断D.【详解】由题意知定义在R 上的函数()f x 满足()()2f x f x =+，即2为函数()f x 的周期，当[]3,4x ∈时，()2f x x =-，当(4,5]x ∈时，()6f x x =-+，故结合函数()f x 的周期，作出其图象如图：结合图象可知()f x 为偶函数，A 正确；结合图象可知1313(2),(2)Z 2222k ,k ,,k +-∈为()f x 的对称中心，B 错误；对于C ，结合图象知()f x 的增区间为[]()21,22Z k k k ++∈，正确，对于D ，作出函数方程ln y x =的图象，由图象可知ln y x =和()f x 的图象有5个交点，故方程()ln 0f x x -=有5个实数解，D 正确，故选：ACD【点睛】关键点睛：本题考查了函数的奇偶性以及周期性和方程的解的问题，综合性较强，解答的关键是明确函数的性质，结合性质和解析式作出其图象，数形结合，解决问题.13．3-【分析】由题意得1,22是方程220ax bx ++=的两个根，由根与系数的关系求出,a b 即可.【详解】由题意可知，1,22是方程220ax bx ++=的两个根，且0a >，由根与系数的关系得122b a +=-且1222a⨯=，解得2,5a b ==-，则3a b +=-.故答案为：3-.14．4【分析】根据题意求出加密密钥的幂函数以及解密密钥指数函数，再根据接受方得到明文“9”，进行逆运算，即可求得答案.【详解】设加密密钥为幂函数1y x α=，则由题意得1932,αα=∴=，即121y x =设解密密钥为指数函数2x y a =，则3273a ,a =∴=，即23xy =，故接受方得到明文“9”，则932t ,t =∴=，则1224x ,x =∴=，即发送方发送的明文为4，故答案为：415．0【分析】由已知利用三角函数的诱导公式分别求得5cos()6πα+与4sin()3πα+的值，则答案可求．【详解】解：∵cos()6πα-=∴5cos()cos[()]66ππαπα+=--cos()6πα=--=4sin(sin()33ππαα+=-+sin ()26ππα⎡⎤=---=⎢⎥⎣⎦cos()6πα--=∴54cos()sin(63ππαα+-+(0=-=，故答案为：0．【点睛】本题主要考查三角函数的化简求值，考查诱导公式的应用，属于基础题．16．334+【分析】先表示出()f x 的解析式，然后作出()f x 的图象，根据图象求解出最大值；结合图象分析值域为3,24⎡⎤⎢⎥⎣⎦时定义域的情况，由此确定出,m n 的取值情况，即可求n m -的最大值.【详解】当23333x x x -+=--+时，解得1x =或3x =，所以()(][)()233,,13,33,1,3x x f x x x x ∞∞⎧--+∈-⋃+⎪=⎨-+∈⎪⎩，作出()f x 的图象如下图所示：由图象可知：当3x =时，()f x 有最大值，所以()()max 33f x f ==；当()34f x =时，解得34x =或32或214；当()2f x =时，x =4x =，由图象可知：当33,42m ⎡⎤∈⎢⎥⎣⎦，n =()f x 的值域为3,24⎡⎤⎢⎥⎣⎦，此时n m -的最大值为333244+-=；当214,4m n ==时，()f x 的值域为3,24⎡⎤⎢⎥⎣⎦，此时5344n m +-=<，由上可知，n m -的最大值为34+，故答案为：3【点睛】思路点睛：本题考查取最小值函数的应用，处理这一类函数时，图象法是首选方法，通过数形结合的思想能高效的将问题简化.常见的图象应用的命题角度有：（1）确定方程根的数目；（2）求参数范围；（3）解不等式；（4）研究函数性质.17．(1){}12x x ≤<(2)1,12⎡⎤⎢⎥⎣⎦【分析】（1）根据2m =，求出集合B ，再根据集合的交集运算，即可求出结果；（2）先求出R B ð，再根据R A B ⊆ð，可得1221m m ≤⎧⎨≤+⎩，求解不等式即可.【详解】（1）解：当2m =时，{2B x x =<或}5x >，又{}12A x x =≤≤，所以{}12A B x x ⋂=≤<；（2）因为{B x x m =<或}21,0x m m >+>，所以{}R 21B x m x m =≤≤+ð，又R A B ⊆ð，所以1221m m ≤⎧⎨≤+⎩，解得112m ≤≤，即1,12m ⎡⎤∈⎢⎥⎣⎦.所以实数m 的取值范围1,12⎡⎤⎢⎥⎣⎦.18．（1）103-（2）12【解析】（1）先求出tan α，代入即可.（2）化简求值即可.【详解】因为sin cos 5αα-=，所以()2sin co 8s 5αα-=2222sin 2sin cos cos 8sin cos 5αααααα-+=+，即22tan 2tan 18tan 15ααα-+=+解得：1tan 3tan =3αα=--或又3,24παπ⎛⎫∈ ⎪⎝⎭,所以tan 3α=-则1110tan =3tan 33αα+--=-（2）()()()cos 2cos 2sin cos 2πααπαπα⎛⎫--+ ⎪⎝⎭--+-sin 2cos tan 2321sin cos tan 1312αααααα++-+====++-+【点睛】此题考查三角函数的化简求值，注意诱导公式的使用，属于简单题目.19．（1）[]0,6；（2）{}22,2,33x k x k k Z x x k k Z ππππππ⎧⎫-≤≤+∈⋃=+∈⎨⎬⎩⎭.【分析】（1）变形得出()231cos 24f x x ⎛⎫=-- ⎪⎝⎭，由1cos 1x -≤≤结合二次函数的基本性质可求得函数()f x 的值域；（2）将不等式变形为22cos cos 10x x +-≥，结合1cos 1x -≤≤可求得cos x 的取值范围，进而可求得x 的取值范围，即可得解.【详解】（1）()22231sin 3cos 3cos 3cos 2cos 24f x x x x x x ⎛⎫=--+=-+=-- ⎪⎝⎭ ，1cos 1x -≤≤ ，则531cos 222x -≤-≤-，所以，21325cos 424x ⎛⎫≤-≤ ⎪⎝⎭，所以，()06f x ≤≤，因此，函数()f x 值域为[]0,6；（2）由()75cos 22f x x ≥-+可得275cos 3cos 2cos 22x x x -+≥-+，即211cos cos 022x x +-≥，即22cos cos 10x x +-≥，解得1cos 2≥x 或cos 1x ≤-，因为1cos 1x -≤≤，1cos 12x ∴≤≤或cos 1x =-.解不等式1cos 12x ≤≤可得()2233k x k k Z ππππ-≤≤+∈，解方程cos 1x =-可得()2x k k =π+π∈Z .因此，不等式()75cos 22f x x ≥-+的解集为{}22,2,33x k x k k Z x x k k Z ππππππ⎧⎫-≤≤+∈⋃=+∈⎨⎬⎩⎭.【点睛】方法点睛：形如()2cos cos 0y a x b x c a =++≠型函数值域的求解，一般利用换元cos t x =，将问题转化为求二次函数2y at bt c =++在区间[]1,1-上的值域，结合二次函数的基本性质求解.20．(1)0.50.520.065n n r -=-⨯（*n ∈N ）(2)6次【分析】（1）由题意得02r =，1 1.94r =，当1n =时，求得0.5p =-，得到n r 的表达式.（2）由0.08n r ≤结合对数运算求得 5.3n ≥即可.【详解】（1）由题意得02r =，1 1.94r =，所以当1n =时，()0.510015p r r r r +=--⋅，即()0.51.9422 1.945p +=--⋅，解得0.5p =-，所以0.50.520.065n n r -=-⨯（*n ∈N ），故改良后所排放的废气中含有的污染物数量的函数模型为0.50.520.065n n r -=-⨯（*n ∈N ）.（2）由题意可得0.50.520.0650.08n n r -=-⨯≤，整理得0.50.5532n -≥两边同时取常用对数，得lg 3205055.lg .n -≥，整理得5lg 2211lg 2n ≥⨯+-，将lg 20.3=代入，可得5lg 230211 5.31lg 27⨯+=+≈-，所以 5.3n ≥，又因为*n ∈N ，所以6n ≥，综上，至少进行6次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.21．(1)0；(2)()1,1-；(3)11a ≤-.【分析】（1）代值计算即可得解；（2）利用指数函数的值域以及不等式的性质可求得函数()f x 的值域；（3）令()()1,1t f x =∈-，()()22h t g x t at ==-，分1a ≥、1a ≤-、11a -<<三种情况讨论，分析函数()h t 在()1,1-上的单调性，根据题意可得出关于a 的不等式，综合可得出实数a 的取值范围.【详解】（1）解：()()22221112121433422012121415514f f -------+=+=+=-=++++.（2）解：()()212212121x x x f x -++==-++.20x > ，则211x +>，则20221x <<+，所以，211121x -<-<+，∴函数()f x 的值域为()1,1-.（3）解：()()()()()2224222122121x x a g x f x a f x a f x af x ⎛⎫⎡⎤⎡⎤⎡⎤=-+=--=- ⎪⎣⎦⎣⎦⎣⎦++⎝⎭，令()t f x =，则()()22g x h t t at ==-，()1,1t ∈-，函数()h t 的对称轴为直线t a =.①当1a ≥时，函数()h t 在()1,1-上单调递减，()()()()12113g x g x h h ∴-<--≤，()()12123a a ∴+--≤，解得34a ≤，此时a 的取值不存在；②当1a ≤-时，函数()h t 在()1,1-上单调递增，()()()()12113g x g x h h ∴-<--≤，()()12123a a ∴--+≤，解得34a ≥-，此时a 的取值不存在；③当11a -<<时，函数()h t 在()1,a -上单调递减，在(),1a 上单调递增，()()()()121g x g x h h a ∴-<--，且()()()()121g x g x h h a -<-，所以，()()()()2211231123h h a a a h h a a a ⎧--=++≤⎪⎨-=-+≤⎪⎩，解得11a ≤≤，此时11a ≤≤.综上，实数a的取值范围为11a ≤-.22．(1)1-(2)()(),20,∞∞--⋃+(3)()21-，【分析】（1）根据偶函数的定义建立方程，解出即可；（2）考查函数在R 的单调性，根据条件转化不等式，解出即可；（3）根据题意可知方程()()f x g x =有两个不同的根，化简方程后，列出条件，解出即可.【详解】（1）函数的定义域为R ，因为函数()()2log 41x f x kx =++为偶函数．所以()()f x f x -=，即()()22log 41log 41x x kx kx -+-=++，所以()()222log 41log 41x x kx -=+-+22414log log 4241x x x x x -+===-+，所以1k =-；（2）因为()()222411log 41log log 222x x x x x f x x ⎛⎫+⎛⎫=+-==+ ⎪ ⎪⎝⎭⎝⎭，当0x ≥时，21x ≥，122x xy =+单调递增，所以()f x 在[)0,∞+上单调递增，又函数()f x 为偶函数，所以函数()f x 在(],0∞-上单调递减；因为()()211f m f m +>-，所以211m m +>-，解得2m <-或0m >，所以不等式的解集为()(),20,∞∞--⋃+（3）因为函数()f x 与()g x 图象有2个公共点，所以方程()()f x g x =有两个不同的根，方程即为()()22log 41log 2x x x a a +-=⋅+，可化为4112222x xx x x a a +⋅+==+，则有20x a a ⋅+>，0a >，设20x t =>，则1at a t t+=+，即()2110a t at -+-=，又2x t =在R 上单调递增，所以方程()2110a t at -+-=有两个不等的正根；所以()()210Δ411001101a a a a a a -≠⎧⎪=--⨯->⎪⎪⎨->-⎪⎪->⎪-⎩，解得21a <<，所以a的取值范围为()21，．。

江苏省南通第一中学2019-2020学年度第二学期暑假作业检测高一数学试卷一、选择题：（本大题共8小题，共40.0分） 1. 下列集合中与{1,9}是同一集合的是()A. {{1},{9}}B. {(1,9)}C. {(9,1)}D. {9,1}2. 设21log 2a =，2log 3b =，231()4c =，则()A. c a b <<B. b a c <<C. a c b <<D. c b a <<3. 给出函数()f x ，()g x 如表，则(())f g x 的值域为().x1 2 3 4 ()g x1133A. {4,2}B. {1,3}C. {}1,2,3,4D. 以上情况都有可能4. 计算2tan123()(4cos 122)sin12︒︒︒-=-A. 4B. 2-C. 4-D. 25. 已知定义在R 上的函数()y f x =满足下列三个条件： ①对任意的x R ∈都有(2)()f x f x +=-； ②对于任意的1202x x <，都有12()();f x f x <③(2)y f x =+的图象关于y 轴对称.则下列结论中正确的是().A. (4.5)(6.5)(7)f f f <<B. (7)(6.5)(4.5)f f f <<C. (7)(4.5)(6.5)f f f <<D. (4.5)(7)(6.5)f f f <<6. 已知函数cos(sin )y x =，则下列结论正确的是()A. 它是奇函数B. 值域为[cos1,1]C. 它不是周期函数D. 定义域为[1,1]-7. 已知a 、b 是平面内两个互相垂直的单位向量，若向量c 满足()()0c a c b -⋅-=，则||c 的最大值是() A. 1B. 2C. 2D.228. 如图，在正四棱锥S ABCD -中，,,M N E 分别是,,CD SC BC 的中点，点P 在线段MN 上运动，有如下结论：①PE AC ⊥；②//PE BD ；③//PE 平面SBD ；④PE ⊥平面.SAC 其中正确结论的个数是()A. 1B. 2C. 3D. 4二、不定项选择题（本大题共4小题，共20.0分）9. 设某大学的女生体重y (单位：kg )与身高x (单位：cm )具有线性相关关系，根据一组样本数据(x i ，y i )(i ＝1，2，…，n)，用最小二乘法建立的回归方程为y ^＝0.85x －85.71，则下列结论中正确的是( )A . y 与x 不具有正的线性相关关系B . 回归直线过样本点的中心(x ，y )C . 若该大学某女生身高增加1 cm ，则其体重约增加0.85 kgD . 若该大学某女生身高为170 cm ，则可断定其体重必为58.79 kg10. 如图，在ABC 中，BC 边上的中线AD 长为3，且2BD =，36sin 8B =，则()A. 6sin 4BAD ∠=B. 1cos 4ADC ∠=C. 10AC =D. ABC 外接圆的面积为128.27π11. 在平面直角坐标系xOy 中，已知圆O ：x 2＋y 2＝4，直线l ：12x －5y ＋c ＝0(其中c 为常数)，下列有关直线l 与圆O 的命题中正确的是( )A. 当c ＝0时，圆O 上有四个不同点到直线l 的距离为1B. 若圆O 上恰有三个不同点到直线l 的距离为1，则c ＝13C. 若圆O 上有四个不同点到直线l 的距离为1，则－13<c <13D. 若圆O 上恰有两个不同点到直线l 的距离为1，则13<c <3912. 下列说法正确的是()A. 函数2211y x x =-+-是偶函数，但不是奇函数B. 函数()f x 的值域是[2,2]-，则函数(1)f x +的值域为[2,2]-C. 设函数()y f x =定义域为R ，则函数(1)y f x =-与(1)y f x =-的图象关于y 轴对称D. 一条曲线2|3|y x =-和直线()y a a R =∈的公共点个数是m ，则m 的值不可能是1x1 2 3 4 ()f x4321三、填空题（本大题共4小题，共20.0分）13. 若点P (2，4)，Q (3，y 0)均在幂函数y ＝f (x )的图象上，则实数y 0＝________． 14. 设α是第二象限角，P (x ，4)为其终边上的一点，且cos α＝15x ，则tan α＝________．15. 已知在正四棱锥P ABCD 中，底面边长为2，高为3，则此正四棱锥P ABCD 的表面积为________． 16. 若非零向量a ，b 满足|a |＝3|b |＝|a ＋2b |，则a 与b 的夹角θ的余弦值为________． 四、解答题： 17. (1)化简：a 43－8a 13b4b 23＋23ab ＋a23÷⎝ ⎛⎭⎪⎫1－23b a ×3a ； (2) 若x log 34＝1，求23x ＋2－3x2x ＋2－x 的值；18. 某高三理科班共有60名同学参加某次考试，从中随机挑选出5名同学，他们的数学成绩x(单位：分)与物理成绩y(单位：分)如下表：数学成绩x 145 130 120 105 100 物理成绩y110901027870数据表明y 与x 之间有较强的线性关系． (1) 求y 关于x 的线性回归方程；(2) 该班一名同学的数学成绩为110分，利用(1)中的回归方程，估计该同学的物理成绩．参考数据：回归直线的系数b ^＝∑i ＝1n（x i －x ）（y i －y ）∑i ＝1n（x i －x ）2，a ^＝y －b ^x .19. 在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，3a cos B ＝b sin A . (1) 求角B 的大小；(2) 设AD 是BC 边上的中线，若AD ⊥AB ，AB ＝2，求AC 的长．20. 在平面直角坐标系xOy 中，记二次函数f (x )＝x 2＋2x ＋b (x ∈R)与两坐标轴有三个交点，经过三个交点的圆记为C .(1) 求实数b 的取值范围；(2) 求圆C 的方程；(3) 问：圆C 是否经过定点(其坐标与b 的值无关)？请证明你的结论．21. 如图，在四棱锥P ABCD 中，底面ABCD 是正方形，P A ⊥平面ABCD ，且P A ＝AD ＝2，点E 为线段PD 的中点．(1) 求证：PB ∥平面AEC ；(2) 求证：AE ⊥平面PCD ； (3) 求三棱锥APCE 的体积．22. 已知函数f (x )＝x 2－ax －6(a 为常数，a ∈R).给出下列四个函数：①g 1(x )＝2x ＋1；②g 2(x )＝3x ；③g 3(x )＝log 2x ；④g 4(x )＝cos x .(1) 当a ＝5时，求不等式f (g 2(x ))≥0的解集； (2) 求函数y ＝f (g 4(x ))的最小值；(3) 在给出的四个函数中，请选择一个函数(不需写出选择过程和理由)，该函数记为g (x )，g (x )满足条件：存在实数a ，使得关于x 的不等式f (g (x ))≤0的解集为[s ，t ]，其中常数s ，t ∈R ，且s ＞0.对选择的g (x )和任意x ∈[2，4]，不等式f (g (x ))≤0恒成立，求实数a 的取值范围．。

2012年江苏省高考数学试卷参考答案与试题解析一、填空题：本大题共14小题.每小题5分.共计70分．请把答案填写在答题卡相应位置上．1．（5分）（2012•江苏）已知集合A={1.2.4}.B={2.4.6}.则A∪B={1.2.4.6} ．考点：并集及其运算．专题：集合．分析：由题意.A.B两个集合的元素已经给出.故由并集的运算规则直接得到两个集合的并集即可解答：解：∵A={1.2.4}.B={2.4.6}.∴A∪B={1.2.4.6}故答案为{1.2.4.6}点评：本题考查并集运算.属于集合中的简单计算题.解题的关键是理解并的运算定义2．（5分）（2012•江苏）某学校高一、高二、高三年级的学生人数之比为3：3：4.现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本.则应从高二年级抽取15 名学生．考点：分层抽样方法．专题：概率与统计．分析：根据三个年级的人数比.做出高二所占的比例.用要抽取得样本容量乘以高二所占的比例.得到要抽取的高二的人数．解答：解：∵高一、高二、高三年级的学生人数之比为3：3：4.∴高二在总体中所占的比例是=.∵用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本.∴要从高二抽取.故答案为：15点评：本题考查分层抽样方法.本题解题的关键是看出三个年级中各个年级所占的比例.这就是在抽样过程中被抽到的概率.本题是一个基础题．3．（5分）（2012•江苏）设a.b∈R.a+bi=（i为虚数单位）.则a+b的值为8 ．考点：复数代数形式的乘除运算；复数相等的充要条件．专题：数系的扩充和复数．分析：由题意.可对复数代数式分子与分母都乘以1+2i.再由进行计算即可得到a+bi=5+3i.再由复数相等的充分条件即可得到a.b的值.从而得到所求的答案解答：解：由题.a.b∈R.a+bi=所以a=5.b=3.故a+b=8故答案为8点评：本题考查复数代数形式的乘除运算.解题的关键是分子分母都乘以分母的共轭.复数的四则运算是复数考查的重要内容.要熟练掌握.复数相等的充分条件是将复数运算转化为实数运算的桥梁.解题时要注意运用它进行转化．4．（5分）（2012•江苏）图是一个算法流程图.则输出的k的值是 5 ．考点：循环结构．专题：算法和程序框图．分析：利用程序框图计算表达式的值.判断是否循环.达到满足题目的条件.结束循环.得到结果即可．解答：解：1﹣5+4=0＞0.不满足判断框．则k=2.22﹣10+4=﹣2＞0.不满足判断框的条件.则k=3.32﹣15+4=﹣2＞0.不成立.则k=4.42﹣20+4=0＞0.不成立.则k=5.52﹣25+4=4＞0.成立.所以结束循环.输出k=5．故答案为：5．点评：本题考查循环框图的作用.考查计算能力.注意循环条件的判断．5．（5分）（2012•江苏）函数f（x）=的定义域为（0.] ．考点：对数函数的定义域．专题：函数的性质及应用．分析：根据开偶次方被开方数要大于等于0.真数要大于0.得到不等式组.根据对数的单调性解出不等式的解集.得到结果．解答：解：函数f（x）=要满足1﹣2≥0.且x＞0∴.x＞0∴.x＞0.∴.x＞0.∴0.故答案为：（0.]点评：本题考查对数的定义域和一般函数的定义域问题.在解题时一般遇到.开偶次方时.被开方数要不小于0.；真数要大于0；分母不等于0；0次方的底数不等于0.这种题目的运算量不大.是基础题．6．（5分）（2012•江苏）现有10个数.它们能构成一个以1为首项.﹣3为公比的等比数列.若从这10个数中随机抽取一个数.则它小于8的概率是．考点：等比数列的性质；古典概型及其概率计算公式．专题：等差数列与等比数列；概率与统计．分析：先由题意写出成等比数列的10个数为.然后找出小于8的项的个数.代入古典概论的计算公式即可求解解答：解：由题意成等比数列的10个数为：1.﹣3.（﹣3）2.（﹣3）3…（﹣3）9其中小于8的项有：1.﹣3.（﹣3）3.（﹣3）5.（﹣3）7.（﹣3）9共6个数这10个数中随机抽取一个数.则它小于8的概率是P=故答案为：点评：本题主要考查了等比数列的通项公式及古典概率的计算公式的应用.属于基础试题7．（5分）（2012•江苏）如图.在长方体ABCD﹣A1B1C1D1中.AB=AD=3cm.AA1=2cm.则四棱锥A ﹣BB1D1D的体积为 6 cm3．考点：棱柱、棱锥、棱台的体积．专题：空间位置关系与距离；立体几何．分析：过A作AO⊥BD于O.求出AO.然后求出几何体的体积即可．解答：解：过A作AO⊥BD于O.AO是棱锥的高.所以AO==.所以四棱锥A﹣BB1D1D的体积为V==6．故答案为：6．点评：本题考查几何体的体积的求法.考查空间想象能力与计算能力．8．（5分）（2012•江苏）在平面直角坐标系xOy中.若双曲线的离心率为.则m的值为 2 ．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：由双曲线方程得y2的分母m2+4＞0.所以双曲线的焦点必在x轴上．因此a2=m＞0.可得c2=m2+m+4.最后根据双曲线的离心率为.可得c2=5a2.建立关于m的方程：m2+m+4=5m.解之得m=2．解答：解：∵m2+4＞0∴双曲线的焦点必在x轴上因此a2=m＞0.b2=m2+4∴c2=m+m2+4=m2+m+4∵双曲线的离心率为.∴.可得c2=5a2.所以m2+m+4=5m.解之得m=2故答案为：2点评：本题给出含有字母参数的双曲线方程.在已知离心率的情况下求参数的值.着重考查了双曲线的概念与性质.属于基础题．9．（5分）（2012•江苏）如图.在矩形ABCD中.AB=.BC=2.点E为BC的中点.点F在边CD 上.若=.则的值是．考点：平面向量数量积的运算．专题：平面向量及应用．分析：根据所给的图形.把已知向量用矩形的边所在的向量来表示.做出要用的向量的模长.表示出要求得向量的数量积.注意应用垂直的向量数量积等于0.得到结果．解答：解：∵.====||=.∴||=1.||=﹣1.∴=（）（）==﹣=﹣2++2=.故答案为：点评：本题考查平面向量的数量积的运算．本题解题的关键是把要用的向量表示成已知向量的和的形式.本题是一个中档题目．10．（5分）（2012•江苏）设f（x）是定义在R上且周期为2的函数.在区间[﹣1.1]上.f （x）=其中a.b∈R．若=.则a+3b的值为﹣10 ．考点：函数的周期性；分段函数的解析式求法及其图象的作法．专题：函数的性质及应用．分析：由于f（x）是定义在R上且周期为2的函数.由f（x）的表达式可得f（）=f（﹣）=1﹣a=f（）=；再由f（﹣1）=f（1）得2a+b=0.解关于a.b的方程组可得到a.b的值.从而得到答案．解答：解：∵f（x）是定义在R上且周期为2的函数.f（x）=.∴f（）=f（﹣）=1﹣ a.f（）=；又=.∴1﹣a=①又f（﹣1）=f（1）.∴2a+b=0.②由①②解得a=2.b=﹣4；∴a+3b=﹣10．故答案为：﹣10．点评：本题考查函数的周期性.考查分段函数的解析式的求法.着重考查方程组思想.得到a.b的方程组并求得a.b的值是关键.属于中档题．（2012•江苏）设α为锐角.若cos（α+）=.则sin（2α+）的值为．11．（5分）考点：三角函数中的恒等变换应用；两角和与差的余弦函数；两角和与差的正弦函数；二倍角的正弦．专题：三角函数的求值；三角函数的图像与性质．分析：先设β=α+.根据cosβ求出sinβ.进而求出sin2β和cos2β.最后用两角和的正弦公式得到sin（2α+）的值．解答：解：设β=α+.∴sinβ=.s in2β=2sinβcosβ=.cos2β=2cos2β﹣1=.∴sin（2α+）=sin（2α+﹣）=sin（2β﹣）=sin2βcos﹣cos2βsin=．故答案为：．点评：本题要我们在已知锐角α+的余弦值的情况下.求2α+的正弦值.着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式.考查了三角函数中的恒等变换应用.属于中档题．12．（5分）（2012•江苏）在平面直角坐标系xOy中.圆C的方程为x2+y2﹣8x+15=0.若直线y=kx﹣2上至少存在一点.使得以该点为圆心.1为半径的圆与圆C有公共点.则k的最大值是．考点：圆与圆的位置关系及其判定；直线与圆的位置关系．专题：直线与圆．分析：由于圆C的方程为（x﹣4）2+y2=1.由题意可知.只需（x﹣4）2+y2=1与直线y=kx﹣2有公共点即可．解答：解：∵圆C的方程为x2+y2﹣8x+15=0.整理得：（x﹣4）2+y2=1.即圆C是以（4.0）为圆心.1为半径的圆；又直线y=kx﹣2上至少存在一点.使得以该点为圆心.1为半径的圆与圆C有公共点.∴只需圆C′：（x﹣4）2+y2=1与直线y=kx﹣2有公共点即可．设圆心C（4.0）到直线y=kx﹣2的距离为d.则d=≤2.即3k2﹣4k≤0.∴0≤k≤．∴k的最大值是．故答案为：．点评：本题考查直线与圆的位置关系.将条件转化为“（x﹣4）2+y2=4与直线y=kx﹣2有公共点”是关键.考查学生灵活解决问题的能力.属于中档题．13．（5分）（2012•江苏）已知函数f（x）=x2+ax+b（a.b∈R）的值域为[0.+∞）.若关于x 的不等式f（x）＜c的解集为（m.m+6）.则实数c的值为9 ．考点：一元二次不等式的应用．专题：函数的性质及应用；不等式的解法及应用．分析：根据函数的值域求出a与b的关系.然后根据不等式的解集可得f（x）=c的两个根为m.m+6.最后利用根与系数的关系建立等式.解之即可．解答：解：∵函数f（x）=x2+ax+b（a.b∈R）的值域为[0.+∞）.∴f（x）=x2+ax+b=0只有一个根.即△=a2﹣4b=0则b=不等式f（x）＜c的解集为（m.m+6）.即为x2+ax+＜c解集为（m.m+6）.则x2+ax+﹣c=0的两个根为m.m+6∴|m+6﹣m|==6解得c=9故答案为：9点评：本题主要考查了一元二次不等式的应用.以及根与系数的关系.同时考查了分析求解的能力和计算能力.属于中档题．14．（5分）（2012•江苏）已知正数a.b.c满足：5c﹣3a≤b≤4c﹣a.clnb≥a+clnc.则的取值范围是[e.7] ．考点：导数在最大值、最小值问题中的应用；不等式的综合．专题：导数的综合应用；不等式的解法及应用．分析：由题意可求得≤≤2.而5×﹣3≤≤4×﹣1.于是可得≤7；由c ln b≥a+c ln c可得0＜a≤cln.从而≥.设函数f（x）=（x＞1）.利用其导数可求得f （x）的极小值.也就是的最小值.于是问题解决．解答：解：∵4c﹣a≥b＞0∴＞.∵5c﹣3a≤4c﹣a.∴≤2．从而≤2×4﹣1=7.特别当=7时.第二个不等式成立．等号成立当且仅当a：b：c=1：7：2．又clnb≥a+clnc.∴0＜a≤cln.从而≥.设函数f（x）=（x＞1）.∵f′（x）=.当0＜x＜e时.f′（x）＜0.当x＞e时.f′（x）＞0.当x=e时.f′（x）=0.∴当x=e时.f（x）取到极小值.也是最小值．∴f（x）min=f（e）==e．等号当且仅当=e.=e成立．代入第一个不等式知：2≤=e≤3.不等式成立.从而e可以取得．等号成立当且仅当a：b：c=1：e：1．从而的取值范围是[e.7]双闭区间．点评：本题考查不等式的综合应用.得到≥.通过构造函数求的最小值是关键.也是难点.考查分析与转化、构造函数解决问题的能力.属于难题．二、解答题：本大题共6小题.共计90分．请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤．15．（14分）（2012•江苏）在△ABC中.已知．（1）求证：tanB=3tanA；（2）若cosC=.求A的值．考点：解三角形；平面向量数量积的运算；三角函数中的恒等变换应用．专题：三角函数的求值；解三角形；平面向量及应用．分析：（1）利用平面向量的数量积运算法则化简已知的等式左右两边.然后两边同时除以c 化简后.再利用正弦定理变形.根据cosAcosB≠0.利用同角三角函数间的基本关系弦化切即可得到tanB=3tanA；（2）由C为三角形的内角.及cosC的值.利用同角三角函数间的基本关系求出sinC的值.进而再利用同角三角函数间的基本关系弦化切求出tanC的值.由tanC的值.及三角形的内角和定理.利用诱导公式求出tan（A+B）的值.利用两角和与差的正切函数公式化简后.将tanB=3tanA代入.得到关于tanA的方程.求出方程的解得到tanA的值.再由A为三角形的内角.利用特殊角的三角函数值即可求出A的度数．解答：解：（1）∵•=3•.∴cb cosA=3cacosB.即bcosA=3acosB.由正弦定理=得：sinBcosA=3sinAcosB.又0＜A+B＜π.∴cosA＞0.cosB＞0.在等式两边同时除以cosAcosB.可得tanB=3tanA；（2）∵cosC=.0＜C＜π.sinC==.∴tanC=2.则tan[π﹣（A+B）]=2.即tan（A+B）=﹣2.∴=﹣2.将tanB=3tanA代入得：=﹣2.整理得：3tan2A﹣2tanA﹣1=0.即（tanA﹣1）（3tanA+1）=0.解得：tanA=1或tanA=﹣.又cosA＞0.∴tanA=1.又A为三角形的内角.则A=．点评：此题属于解三角形的题型.涉及的知识有：平面向量的数量积运算法则.正弦定理.同角三角函数间的基本关系.诱导公式.两角和与差的正切函数公式.以及特殊角的三角函数值.熟练掌握定理及公式是解本题的关键．16．（14分）（2012•江苏）如图.在直三棱柱ABC﹣A1B1C1中.A1B1=A1C1.D.E分别是棱1上的点（点D 不同于点C）.且AD⊥DE.F为B1C1的中点．求证：（1）平面ADE⊥平面BCC1B1；（2）直线A1F∥平面ADE．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：空间位置关系与距离；立体几何．分析：（1）根据三棱柱ABC﹣AB1C1是直三棱柱.得到CC1⊥平面ABC.从而AD⊥CC1.结合已知1条件AD⊥DE.DE、CC1是平面BCC1B1内的相交直线.得到AD⊥平面BCC1B1.从而平面ADE⊥平面BCC1B1；（2）先证出等腰三角形△A1B1C1中.A1F⊥B1C1.再用类似（1）的方法.证出A1F⊥平面BCC1B1.结合AD⊥平面BCC1B1.得到A1F∥AD.最后根据线面平行的判定定理.得到直线A1F∥平面ADE．解答：解：（1）∵三棱柱ABC﹣AB1C1是直三棱柱.1∴CC1⊥平面ABC.∵AD⊂平面ABC.∴AD⊥CC1又∵AD⊥DE.DE、CC1是平面BCC1B1内的相交直线∴AD⊥平面BCC1B1.∵AD⊂平面ADE∴平面ADE⊥平面BCC1B1；（2）∵△A1B1C1中.A1B1=A1C1.F为B1C1的中点∴A1F⊥B1C1.∵CC1⊥平面A1B1C1.A1F⊂平面A1B1C1.∴A1F⊥CC1又∵B1C1、CC1是平面BCC1B1内的相交直线∴A1F⊥平面BCC1B1又∵AD⊥平面BCC1B1.∴A1F∥AD∵A1F⊄平面ADE.AD⊂平面ADE.∴直线A1F∥平面ADE．点评：本题以一个特殊的直三棱柱为载体.考查了直线与平面平行的判定和平面与平面垂直的判定等知识点.属于中档题．17．（14分）（2012•江苏）如图.建立平面直角坐标系xOy.x轴在地平面上.y轴垂直于地平面.单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx﹣（1+k2）x2（k＞0）表示的曲线上.其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．（1）求炮的最大射程；（2）设在第一象限有一飞行物（忽略其大小）.其飞行高度为3.2千米.试问它的横坐标a 不超过多少时.炮弹可以击中它？请说明理由．考点：函数模型的选择与应用．专题：函数的性质及应用．分析：（1）求炮的最大射程即求 y=kx﹣（1+k2）x2（k＞0）与x轴的横坐标.求出后应用基本不等式求解．（2）求炮弹击中目标时的横坐标的最大值.由一元二次方程根的判别式求解．解答：解：（1）在 y=kx﹣（1+k2）x2（k＞0）中.令y=0.得 kx﹣（1+k2）x2=0．由实际意义和题设条件知x＞0.k＞0．∴.当且仅当k=1时取等号．∴炮的最大射程是10千米．（2）∵a＞0.∴炮弹可以击中目标等价于存在 k＞0.使ka﹣（1+k2）a2=3.2成立.即关于k的方程a2k2﹣20ak+a2+64=0有正根．由韦达定理满足两根之和大于0.两根之积大于0.故只需△=400a2﹣4a2（a2+64）≥0得a≤6．此时.k=＞0．∴当a不超过6千米时.炮弹可以击中目标．点评：本题考查函数模型的运用.考查基本不等式的运用.考查学生分析解决问题的能力.属于中档题．18．（16分）（2012•江苏）若函数y=f（x）在x=x0处取得极大值或极小值.则称x0为函数y=f（x）的极值点．已知a.b是实数.1和﹣1是函数f（x）=x3+ax2+bx的两个极值点．（1）求a和b的值；（2）设函数g（x）的导函数g′（x）=f（x）+2.求g（x）的极值点；（3）设h（x）=f（f（x））﹣c.其中c∈[﹣2.2].求函数y=h（x）的零点个数．考点：函数在某点取得极值的条件；函数的零点．专题：导数的综合应用．分析：（1）求出导函数.根据1和﹣1是函数的两个极值点代入列方程组求解即可．（2）由（1）得f（x）=x3﹣3x.求出g′（x）.令g′（x）=0.求解讨论即可．（3）先分|d|=2和|d|＜2讨论关于的方程f（x）=d的情况；再考虑函数y=h（x）的零点．解答：解：（1）由 f（x）=x3+ax2+bx.得f′（x）=3x2+2ax+b．∵1和﹣1是函数f（x）的两个极值点.∴f′（1）=3﹣2a+b=0.f′（﹣1）=3+2a+b=0.解得a=0.b=﹣3．（2）由（1）得.f（x）=x3﹣3x.∴g′（x）=f（x）+2=x3﹣3x+2=（x﹣1）2（x+2）=0.解得x1=x2=1.x3=﹣2．∵当x＜﹣2时.g′（x）＜0；当﹣2＜x＜1时.g′（x）＞0.∴﹣2是g（x）的极值点．∵当﹣2＜x＜1或x＞1时.g′（x）＞0.∴1不是g（x）的极值点．∴g（x）的极值点是﹣2．（3）令f（x）=t.则h（x）=f（t）﹣c．先讨论关于x的方程f（x）=d根的情况.d∈[﹣2.2]当|d|=2时.由（2 ）可知.f（x）=﹣2的两个不同的根为1和一2.注意到f（x）是奇函数.∴f（x）=2的两个不同的根为﹣1和2．当|d|＜2时.∵f（﹣1）﹣d=f（2）﹣d=2﹣d＞0.f（1）﹣d=f（﹣2）﹣d=﹣2﹣d＜0.∴一2.﹣1.1.2 都不是f（x）=d 的根．由（1）知.f′（x）=3（x+1）（x﹣1）．①当x∈（2.+∞）时.f′（x）＞0.于是f（x）是单调增函数.从而f（x）＞f（2）=2．此时f（x）=d在（2.+∞）无实根．②当x∈（1.2）时.f′（x）＞0.于是f（x）是单调增函数．又∵f（1）﹣d＜0.f（2）﹣d＞0.y=f（x）﹣d的图象不间断.∴f（x）=d在（1.2 ）内有唯一实根．同理.在（一2.一1）内有唯一实根．③当x∈（﹣1.1）时.f′（x）＜0.于是f（x）是单调减函数．又∵f（﹣1）﹣d＞0.f（1）﹣d＜0.y=f（x）﹣d的图象不间断.∴f（x）=d在（一1.1 ）内有唯一实根．因此.当|d|=2 时.f（x）=d 有两个不同的根 x1.x2.满足|x1|=1.|x2|=2；当|d|＜2时.f （x）=d 有三个不同的根x3.x4.x5.满足|x i|＜2.i=3.4.5．现考虑函数y=h（x）的零点：（ i ）当|c|=2时.f（t）=c有两个根t1.t2.满足|t1|=1.|t2|=2．而f（x）=t1有三个不同的根.f（x）=t2有两个不同的根.故y=h（x）有5 个零点．（ i i ）当|c|＜2时.f（t）=c有三个不同的根t3.t4.t5.满足|t i|＜2.i=3.4.5．而f（x）=t i有三个不同的根.故y=h（x）有9个零点．综上所述.当|c|=2时.函数y=h（x）有5个零点；当|c|＜2时.函数y=h（x）有9 个零点．点评：本题考查导数知识的运用.考查函数的极值.考查函数的单调性.考查函数的零点.考查分类讨论的数学思想.综合性强.难度大．19．（16分）（2012•江苏）如图.在平面直角坐标系xOy中.椭圆（a＞b＞0）的左、右焦点分别为F1（﹣c.0）.F2（c.0）．已知（1.e）和（e.）都在椭圆上.其中e为椭圆的离心率．（1）求椭圆的方程；（2）设A.B是椭圆上位于x轴上方的两点.且直线AF1与直线BF2平行.AF2与BF1交于点P．（i）若AF1﹣BF2=.求直线AF1的斜率；（ii）求证：PF1+PF2是定值．直线与圆锥曲线的综合问题；直线的斜率；椭圆的标准方程．考点：圆锥曲线的定义、性质与方程．专题：分（1）根据椭圆的性质和已知（1.e）和（e.）.都在椭圆上列式求解．析：（2）（i）设AF1与BF2的方程分别为x+1=my.x﹣1=my.与椭圆方程联立.求出|AF1|、|BF2|.根据已知条件AF1﹣BF2=.用待定系数法求解；（ii）利用直线AF1与直线BF2平行.点B在椭圆上知.可得..由此可求得PF1+PF2是定值．解答：（1）解：由题设知a2=b2+c2.e=.由点（1.e）在椭圆上.得.∴b=1.c2=a2﹣1．由点（e.）在椭圆上.得∴.∴a2=2∴椭圆的方程为．（2）解：由（1）得F1（﹣1.0）.F2（1.0）.又∵直线AF1与直线BF2平行.∴设AF1与BF2的方程分别为x+1=my.x﹣1=my．设A（x1.y1）.B（x2.y2）.y1＞0.y2＞0.∴由.可得（m2+2）﹣2my1﹣1=0．∴.（舍）.∴|AF1|=×|0﹣y1|=①同理|BF2|=②（i）由①②得|AF1|﹣|BF2|=.∴.解得m2=2．∵注意到m＞0.∴m=．∴直线AF1的斜率为．（ii）证明：∵直线AF1与直线BF2平行.∴.即．由点B在椭圆上知..∴．同理．∴PF1+PF2==由①②得...∴PF1+PF2=．∴PF 1+PF 2是定值．点评： 本题考查椭圆的标准方程.考查直线与椭圆的位置关系.考查学生的计算能力.属于中档题．20．（16分）（2012•江苏）已知各项均为正数的两个数列{a n }和{b n }满足：a n+1=.n ∈N *.（1）设b n+1=1+.n ∈N*.求证：数列是等差数列；（2）设b n+1=•.n ∈N*.且{a n }是等比数列.求a 1和b 1的值．考点： 数列递推式；等差关系的确定；等比数列的性质． 专题： 等差数列与等比数列． 分析：（1）由题意可得.a n+1===.从而可得.可证（2）由基本不等式可得..由{a n }是等比数列利用反证法可证明q==1.进而可求a 1.b 1解答：解：（1）由题意可知.a n+1===∴从而数列{}是以1为公差的等差数列（2）∵a n ＞0.b n ＞0∴从而（*）设等比数列{a n}的公比为q.由a n＞0可知q＞0下证q=1若q＞1.则.故当时.与（*）矛盾0＜q＜1.则.故当时.与（*）矛盾综上可得q=1.a n=a1.所以.∵∴数列{b n}是公比的等比数列若.则.于是b1＜b2＜b3又由可得∴b1.b2.b3至少有两项相同.矛盾∴.从而=∴点评：本题主要考查了利用构造法证明等差数列及等比数列的通项公式的应用.解题的关键是反证法的应用．三、附加题(21选做题：任选2小题作答.22、23必做题）（共3小题.满分40分）21．（20分）（2012•江苏）A．[选修4﹣1：几何证明选讲]如图.AB是圆O的直径.D.E为圆上位于AB异侧的两点.连接BD并延长至点C.使BD=DC.连接AC.AE.DE．求证：∠E=∠C．B．[选修4﹣2：矩阵与变换]已知矩阵A的逆矩阵.求矩阵A的特征值．C．[选修4﹣4：坐标系与参数方程]在极坐标中.已知圆C经过点P（.）.圆心为直线ρsin（θ﹣）=﹣与极轴的交点.求圆C的极坐标方程．D．[选修4﹣5：不等式选讲]已知实数x.y满足：|x+y|＜.|2x﹣y|＜.求证：|y|＜．考点：特征值与特征向量的计算；简单曲线的极坐标方程；不等式的证明；综合法与分析法(选修）．专题：不等式的解法及应用；直线与圆；矩阵和变换；坐标系和参数方程．分析：A．要证∠E=∠C.就得找一个中间量代换.一方面考虑到∠B.∠E是同弧所对圆周角.相等；另一方面根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到．从而得证．B．由矩阵A的逆矩阵.根据定义可求出矩阵A.从而求出矩阵A的特征值．C．根据圆心为直线ρsin（θ﹣）=﹣与极轴的交点求出的圆心坐标；根据圆经过点P（.）.求出圆的半径.从而得到圆的极坐标方程．D．根据绝对值不等式的性质求证．解答：A．证明：连接 AD．∵AB是圆O的直径.∴∠ADB=90°（直径所对的圆周角是直角）．∴AD⊥BD（垂直的定义）．又∵BD=DC.∴AD是线段BC 的中垂线（线段的中垂线定义）．∴AB=AC（线段中垂线上的点到线段两端的距离相等）．∴∠B=∠C（等腰三角形等边对等角的性质）．又∵D.E 为圆上位于AB异侧的两点.∴∠B=∠E（同弧所对圆周角相等）．∴∠E=∠C（等量代换）．B、解：∵矩阵A的逆矩阵.∴A=∴f（λ）==λ2﹣3λ﹣4=0∴λ1=﹣1.λ2=4C、解：∵圆心为直线ρsin（θ﹣）=﹣与极轴的交点.∴在ρsin（θ﹣）=﹣中令θ=0.得ρ=1．∴圆C的圆心坐标为（1.0）．∵圆C 经过点P（.）.∴圆C的半径为PC=1．∴圆的极坐标方程为ρ=2cosθ．D、证明：∵3|y|=|3y|=|2（x+y）﹣（2x﹣y）|≤2|x+y|+|2x﹣y|.|x+y|＜.|2x﹣y|＜.∴3|y|＜.∴点评：本题是选作题.综合考查选修知识.考查几何证明选讲、矩阵与变换、坐标系与参数方程、不等式证明.综合性强22．（10分）（2012•江苏）设ξ为随机变量.从棱长为1的正方体的12条棱中任取两条.当两条棱相交时.ξ=0；当两条棱平行时.ξ的值为两条棱之间的距离；当两条棱异面时.ξ=1．（1）求概率P（ξ=0）；（2）求ξ的分布列.并求其数学期望E（ξ）．考点：离散型随机变量的期望与方差；古典概型及其概率计算公式．专题：概率与统计．分析：（1）求出两条棱相交时相交棱的对数.即可由概率公式求得概率．（2）求出两条棱平行且距离为的共有6对.即可求出相应的概率.从而求出随机变量的分布列与数学期望．解答：解：（1）若两条棱相交.则交点必为正方体8个顶点中的一个.过任意1个顶点恰有3条棱.∴共有8对相交棱.∴P（ξ=0）=．（2）若两条棱平行.则它们的距离为1或.其中距离为的共有6对.∴P（ξ=）=.P（ξ=1）=1﹣P（ξ=0）﹣P（ξ=）=．∴随机变量ξ的分布列是：ξ0 1P∴其数学期望E（ξ）=1×+=．点评：本题考查概率的计算.考查离散型随机变量的分布列与期望.求概率是关键．23．（10分）（2012•江苏）设集合P n={1.2.….n}.n∈N*．记f（n）为同时满足下列条件的集合A的个数：①A⊆P n；②若x∈A.则2x∉A；③若x∈ A.则2x∉A．（1）求f（4）；（2）求f（n）的解析式（用n表示）．考点：函数解析式的求解及常用方法；元素与集合关系的判断；集合的包含关系判断及应用．专题：集合．分析：（1）由题意可得P={1.2.3.4}.符合条件的集合A为：{2}.{1.4}.{2.3}.{1.3.4}.故4可求f（4）（2）任取偶数x∈p n.将x除以2.若商仍为偶数.再除以2….经过k次后.商必为奇数.此时记商为m.可知.若m∈A.则x∈A.⇔k为偶数；若m∉A.则x∈A⇔k为奇数.可求解答：解（1）当n=4时.P={1.2.3.4}.符合条件的集合A为：{2}.{1.4}.{2.3}.{1.3.4}4故f（4）=4（2）任取偶数x∈p n.将x除以2.若商仍为偶数.再除以2….经过k次后.商必为奇数.此时记商为m.于是x=m•2k.其中m为奇数.k∈N*由条件可知.若m∈A.则x∈A.⇔k为偶数若m∉ A.则x∈A⇔k为奇数于是x是否属于A由m是否属于A确定.设Q n是P n中所有的奇数的集合因此f（n）等于Q n的子集个数.当n为偶数时（或奇数时）.P n中奇数的个数是（或）∴点评：本题主要考查了集合之间包含关系的应用.解题的关键是准确应用题目中的定义。