通信原理第10章 数字信号的最佳接收
- 格式:pdf
- 大小:522.91 KB
- 文档页数:32


第一部分 最佳接收机的特点①最佳接收以最小差错概率为准则。
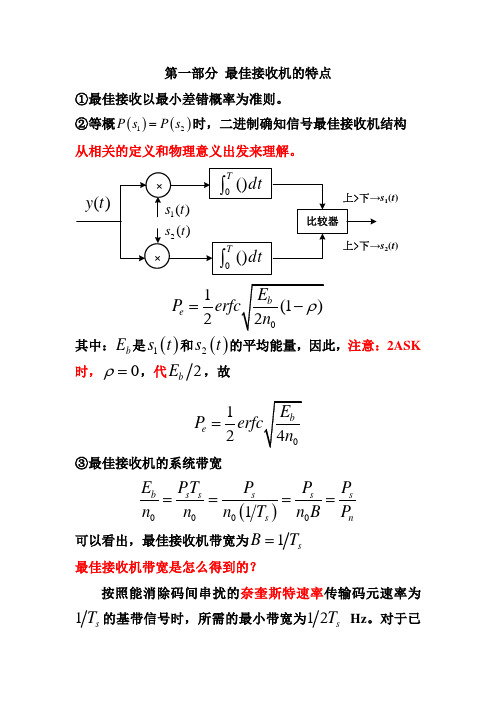
②等概()()12P s P s =时,二进制确知信号最佳接收机结构 从相关的定义和物理意义出发来理解。
s 1(t )s 2(t )12e P =其中:b E 是()1s t 和()2s t 的平均能量,因此,注意:2ASK时,0ρ=,代2b E ,故12e P =③最佳接收机的系统带宽()00001b s ss s s s nE PT P P P n n n T n B P ==== 可以看出,最佳接收机带宽为1s B = 最佳接收机带宽是怎么得到的?按照能消除码间串扰的奈奎斯特速率传输码元速率为1s T 的基带信号时,所需的最小带宽为12s T Hz 。
对于已调信号, 2PSK 、2ASK 和2FSK 信号,若采用最佳接收机,则其占用带宽应当是基带信号带宽的两倍,即恰好是1s T Hz ,相当于单边带调制。
这时,数字频带调制的最大频带利用率为1baud/Hz 。
④最佳接收机和一般接收机输入信噪比的比较实际接收机:2202n a S Sr N n Bσ=== 最佳接收机:0001b E ST S h n n n T=== 讨论:1B r h T ==,实际的性能同于最佳的性能 1B r h T ><,实际的性能劣于最佳的性能 1B r h T<>,实际的性能优于最佳的性能结论:实际中,仅1B T>情况发生,所以实际接收机性能劣于最佳接收机。
第二部分 匹配滤波器能够获得最大信噪比的一种线性滤波器。
①匹配滤波器传输函数和冲激响应s ()()o o n t s t 、2)ω结论:在白噪声背景下,若按0*()()j t H KS eωωω-=设计匹配滤波器,在给定时刻上0t ,获得最大输出信噪比max2o E r n =。
0()()h t Ks t t =-根据物理可实现条件:0()00()00h t t s t t t =<-=<,,注意到0t<时,00t t t ->0()0s t t t =>,结论:匹配滤波器的输入信号()st 必须在它获取最大信噪比时刻0t 之前结束。



第十章数字信号的最佳接收本章主要内容●最佳接收准则●最佳接收机结构●基带系统最佳化10.1 引言“最佳”不是一个绝对概念,而是在某个“最佳准则”下说的相对概念。
数字通信中常用的“最佳”准则:数字通信系统中,信道的传输特性和传输过程中噪声的存在是影响通信性能的两个主要因素。
最大输出信噪比准则——匹配接收最小差错概率准则——相关接收1 最大输出信噪比准则10.2匹配滤波器)(H ω)t (x )t (s )t (n 输出判决)t (y 数字接收滤波器的作用:z 使输出信号尽可能强;z 抑制带外噪声,减小噪声对信号判决的影响。
最佳线性滤波器设计的两种准则:z 输出信号波形与发送波形之间的均方误差最小——维纳滤波器;z 输出信噪比在某一特定时刻最大——匹配滤波器。
要求线性滤波器在t o 时刻有最大信号瞬时功率与噪声平均功率比值。
)t (n )t (s )t (x +=2/n )(P )(S )t (s o n =ωω⇔)t (n )t (s )t (y o o +=∫∞∞−ωωωωπ=d e )(S )(H 21)t (s tj o 输出噪声平均功率∫∫∞∞−∞∞−ωωπ=ω⋅ωπ=d )(H 4n d )2n ()(H 21N 2o o 2o 最佳接收滤波器:不要求滤波器输出信号波形与发送信号波形间相似程度如何,而取决于抽样时刻信号的瞬时功率与噪声的平均功率之比,即使输出信噪比在某一特定时刻上达到最大值,这样有利于正确判决。
(1)匹配滤波器t o 时刻输出信号瞬时功率与噪声平均功率比值∫∫∞∞−∞∞−ωωωπωωωπ==d )(H 4n de )(S )(H 21N )t (s r 2o 2t j o2o o o max0o r r ?)(H =→=ω利用许瓦尔兹(Schwartz )不等式求解∫∫∫∞∞−∞∞−∞∞−ωωπ⋅ωωπ≤ωωωπd )(Y 21d )(X 21d )(Y )(X 21222oo o o n E n d S d H n d S d H r 22/)(21)(4)()(4122222==⋅≤∫∫∫∫∞∞−∞∞−∞∞−∞∞−πωωωωπωωωωπ其中信号s(t)能量∫∫∞∞∞−ωωπ==022d )(S 1df )f (S Eomaxo n E 2r =最大输出信噪比上式取等号时满足)(KY )(X *ω=ω即ot j *e)(KS )(H ω−ω=ω该滤波器就是最大信噪比意义下的最佳线性滤波器,也称匹配滤波器。
)t t (Ks d e )(H 21)t (h o tj −=ωωπ=ω∞∞−∫匹配滤波器的冲激响应是输入信号s (t )的镜象及平移。
匹配滤波器的输出信号波形∫∞∞−τττ−==d )(h )t (s )t (h *)t (s )t (s o )t t (KR )t (s o o −=R(t)为s(t)自相关函数例:求对单个矩形脉冲匹配的匹配滤波器特性。
)t(stτ1)t(htτ1)t(sotτ0τ2∫∞∞−ωτ−ω−−ω==ω)e1(j1dte)t(s)(S jtjootjjtj*e)1e(j1e)(S)(Hω−ωτω−−ω=ω=ω)t(s)tt(s)t(ho−τ=−=⎪⎪⎩⎪⎪⎨⎧<≤−=<≤===∫∫−tttdttdtht ststto,其它)2(,2')0(,')(*)()(ττττττττ在s(t)结束时刻得到最大输出信噪比。
(2)采用匹配滤波器的最佳接收机对于二进制确知信号,最佳接收机结构如图)T t 0()t T (s )t (h 1<<−=)T t 0()t T (s )t (h 2<<−=比较器)(t y MFMF在T 时刻抽样判决,选择最大输出。
时T t =∫∫==TTo dt)t (s )t (y K dz )z (s )z (y K )t (u ∫∫ττ−τ−=τττ−==TT 0o d )T (s )t (y K d )(h )t (y K )t (h *)t (y )t (u zt −=τ令∫−+−=tTt o dzz t T s z y K t u )()()(⎩⎨⎧≤≤−=−=其他0/1)()()(T t T t t h t T s t h 解:例:在双边功率谱为密度n o /2的加性高斯白噪声干扰下,对如下信号设计一个匹配滤波器。
(1)写出匹配滤波器的冲激响应h(t) ,并绘出图形;(2)求出s(t)经过匹配滤波器的输出信号y(t),并绘出图形;(3) 求最大输出信噪比。
⎩⎨⎧≤≤=其他T t 0T /t )t (s )t (h t01Tτττ−=∫d )(h )t (s )t (y T)t (y t1T 2T3/T S(t)的能量3T dt )Tt (E T2==∫最大输出信噪比0maxo n 3T2n E 2r ==ωωπ==∫∫∞∞−∞∞−d )(F 21dt )t (f E 22(能量信号)判决规则xsn+y r消息空间信号空间观察空间噪声空间判决空间带噪声的数字信号的接收,实质上一个统计接收问题,或者说信号接收过程是一个统计判决的过程。
从统计学的观点可以将数字通信系统用一个统计模型表示。
确定y 的统计信息,即可按照一定判决规则确定r。
判决规则xsn+y r消息空间信号空间观察空间噪声空间判决空间带噪声的数字信号的接收,实质上一个统计接收问题,或者说信号接收过程是一个统计判决的过程。
从统计学的观点可以将数字通信系统用一个统计模型表示。
确定y 的统计信息,即可按照一定判决规则确定r。
发送信号{S}:⎟⎟⎠⎞⎜⎜⎝⎛)s (P )s (P )s (P )s (P s s s s m 321m 321LL ∑==m1i i1)s(P 噪声为加性高斯白噪声,且其各抽样值相互独立,在(0,T )观察时间的K 个噪声样值均为正态分布,则n 的统计特性用多维联合概率密度函数表示为(2)信号空间(3)噪声空间发送信号与消息之间通常是一一对应.若m=2,则为二进制数字通信系统。
离散消息源{x}:⎟⎟⎠⎞⎜⎜⎝⎛)x (P )x (P )x (P )x (P x x x x m 321m321L L ∑==m1i i1)x(P (1)消息空间若限带信道的截止频率为f H ,理想抽样频率为2f H ,则在(0,T )内有2 f H T(k)个样值,其平均功率为∫∑≈==T2k1i i2H o dt)t (n T1nTf 21N Tf 2k H =)T t ,f 21t (H<<Δ=Δ且抽样间隔)n (f )n (f )n (f )n (f k 21L ⋅=]n 21exp[)2(1k1i i 2n 2kn ∑=σ−σπ=02n 噪声均值为噪声方差−−−σ]dt )t (n n 1exp[)2(1]dt )t (n 2f 2exp[)2(1)n (f T2o kn T2n 2H kn ∫∫−σπ=σ−σπ=(4)观察空间y=s i (t)+n(t)i=1,2,…m由于n (t )为高斯噪声,y (t )可以看成是均值为S i (t)的正态分布,因此出现信号S i (t)时,y(t)的概率密度函数f Si (y)可表示为}dt )]t (S )t (y [n 1exp{))2(1()y (f T2i o kn si ∫−−σπ=m,...2,1i =——似然函数s]dt )t (y n 1exp[))2(1()y (f T02o kn 1s ∫−σπ=}dt ]1)t (y [n 1exp{))2(1()y (f T2o kn 2s ∫−−σπ=m =20s 1=1s 2=10.4 最小差错概率接收准则1. 最小差错概率准则由于信道噪声的存在,发送x i 时不一定正确判为r i ,从而造成错判。
数字通信中最直观而又合理的最佳接收准则就是“最小差错概率准则”。
发送消息:x 1(0), x 2(1)发送信号:s 1(0), s 2(1)当s 1,s 2在观察时刻取值为a 1,a 2时,y(t)的概率密度函数分别为]}dt ]a )t (y [n 1exp{))2(1()y (f T021o kn 1s ∫−−σπ=]}dt ]a )t (y [n 1exp{))2(1()y (f T22o kn 2s ∫−−σπ=发s 1错判为s 2的概率dy)y (f Q '0y 1s 1∫∞=发s 2错判为s 1的概率dy)y (f Q '0y 2s 2∫∞−=每一次判决的平均错误概率2211e Q )s (P Q )s (P P +=求最佳门限0)y (f )s (P )y (f )s (P y P 'o 2s 2'o 1s 1'oe =−+−=∂∂)s (P )s (P )y (f )y (f 12o 2S o 1S =最佳门限oy (1)似然比判决准则如果按以下规则进行判决,则能使总错误概率最小。
)s (P )s (P )y (f )y (f )s (P )s (P )y (f )y (f 122S 1S 122S 1S <>判为r 1判为r 2当P(s 1)=P(s 2)时,得到似然比准则的一种特例——最大似然准则:22s 1s 12s 1s s ),y (f )y (f s ),y (f )y (f 判为判为<>推广到多进制情况:发送信号有m 个,且它们出现概率相等,则最大似然准则可以表示为isj si s ,j i ,m ,...,2,1j ,m ,...,2,1i );y (f )y (f 判为≠==>这样,收到y 后,分别计算似然函数,然后进行比较。
(2)二进制确知信号的最佳接收机——相关检测器根据似然准则]}dt )]t (s )t (y [n 1exp{)s (P ]}dt )]t (s )t (y [n 1exp{)s (P T22o2T21o 1∫∫−−>−−判s 1出现]}dt )]t (s )t (y [n 1exp{)s (P ]}dt )]t (s )t (y [n 1exp{)s (P T22o2T 021o1∫∫−−<−−判s 2出现设s 1(t)和s 2(t)具有相同能量,则上式可以写成)s (P ln 2n u ),s (P ln 2n u 202101==∫∫∫∫+<++>+T222T11T0122T011s ,dt )t (s )t (y u dt )t (s )t (y u s ,dt )t (s )t (y u dt )t (s )t (y u 判为判为最佳接收机——相关检测器相乘器积分器相加器相乘器积分器相加器比较器)t (y )t (s 1)t (s 21u 2u 输出T t =时刻比较输出一般形式相乘器积分器相乘器积分器比较器)t ()t (s 1)t (s 2输出)s (P )s (P 21=相乘器积分器相乘器积分器选择和判决)t (y )t (s 1)t (s 2输出相乘器)t (s M 积分器M 进制例:设OOK 二进制信号为,传输中受到高斯白噪声的干扰,画出最佳相干接收及非相干接收框图。