数学---河北省衡水市冀州中学2016-2017学年高一下学期期末考试(理)试题A卷

试卷类型：B卷河北冀州中学2016-2017学年度下学期期末高一年级理科数学试题（考试时间：120分钟分值：150分）第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合则= ( )A. B.C.D.2.设变量x，y满足约束条件则目标函数的最小值为( )A. B. 10 C. 6 D.173. 在△ABC中，如果sin A＝sin C，B＝30°，角B所对的边长b＝2，则△ABC的面积为( ) A． B. 1 C．2 D．44.已知点A(1,3),B(4,-1),则与同方向的单位向量是（）A.B.C. D.5.已知等差数列中，前项和为，若，则（）A.36B.40C.42D.456.a，b为正实数，若函数f(x)＝ax3＋bx＋ab－1是奇函数，则f(2)的最小值是( )A．2 B．8 C．4 D．167.若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为 ( )A.5B. 4C.6D.98.函数的图像恒过定点A，若点A在直线上，其中，则的最小值为（）A.B. C.7 D.119.若，则（）A.B.C. D.10.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是()A. B.C.D.111.已知等差数列前n项和为S n，若S13＜0，S12＞0，则在数列中绝对值最小的项为( )A．第5项 B．第7项 C．第6项 D．第8项12.已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为 ( )A. B.C.D.第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分。

把答案直接答在答题纸上。

2016-2017学年河北省衡水中学高一（下）期中数学试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．2．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为BC、BB1的中点，则下列直线中与直线EF相交的是（）A．直线AA1B．直线A1B1C．直线A1D1D．直线B1C1 3．（5分）在空间中，设m，n为两条不同直线，α，β为两个不同平面，则下列命题正确的是（）A．若m∥α且α∥β，则m∥βB．若α⊥β，m⊂α，n⊂β，则m⊥nC．若m⊥α且α∥β，则m⊥βD．若m不垂直于α，且n⊂α，则m必不垂直于n4．（5分）如图，△O'A'B'是水平放置的△OAB的直观图，则△OAB的周长为（）A．B．3C．D．125．（5分）若正四棱锥的侧棱长为，侧面与底面所成的角是45°，则该正四棱锥的体积是（）A．B．C．D．6．（5分）已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O﹣ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）A．B．4πC．D．3π7．（5分）若某空间几何体的三视图如图所示，则该几何体的表面积是（）A．48+πB．48﹣πC．48+2πD．48﹣2π8．（5分）已知棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设面MEF∩面MPQ=l，则下列结论中不成立的是（）A．l∥面ABCDB．l⊥ACC．面MEF与面MPQ不垂直D．当x变化时，l不是定直线9．（5分）已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（）A．B．C．3πD．4π10．（5分）如图，等边△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，下列命题中，错误的是（）A．动点A′在平面ABC上的射影在线段AF上B．恒有平面A′GF⊥平面BCEDC．三棱锥A′﹣EFD的体积有最大值D．异面直线A′E与BD不可能垂直11．（5分）已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的=，则OA与平面ABCD所成的角的余弦值为（）体积为V球A．B．C．D．12．（5分）在底面为正三角形的直棱柱（侧棱垂直于底面的棱柱）ABC﹣A1B1C1中，AB=2，AA1=3，点D为棱BD的中点，点E为A，C上的点，且满足A1E=mEC （m∈R），当二面角E﹣AD﹣C的余弦值为时，实数m的值为（）A．1B．2C．D．3二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点A到平面A1DB的距离为．14．（5分）在三棱锥A﹣BCD中，侧棱AB，AC，AD两两垂直，△ABC、△ACD、△ABD的面积分别为、、，则三棱锥A﹣BCD的外接球的体积为．15．（5分）如图，三棱锥A﹣BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D 两点所经过的路程之和是．16．（5分）在正方体ABCD﹣A1B1C1D1中（如图），已知点P在直线BC1上运动．则下列四个命题：①三棱锥A﹣D1BC的体积不变；②直线AP与平面ACD1所成的角的大小不变；③二面角P﹣AD1﹣C的大小不变；④M是平面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是直线A1D1其中正确命题的编号是．（写出所有正确命题的编号）三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10分）如图，O是圆锥底面圆的圆心，圆锥的轴截面PAB为等腰直角三角形，C为底面圆周上一点．（Ⅰ）若弧的中点为D，求证：AC∥平面POD（Ⅱ）如果△PAB面积是9，求此圆锥的表面积与体积．18．（12分）《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形，且侧棱与底面垂直的棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABM﹣DCP与刍童的组合体中AB=AD，A1B1=A1D1．棱台体积公式：V=（S′++S）h，其中S′，S分别为棱台上、下底面面积，h为棱台高．（Ⅰ）证明：直线BD⊥平面MAC；（Ⅱ）若AB=1，A1D1=2，MA=，三棱锥A﹣A1B1D1的体积V=，求该组合体的体积．19．（12分）如图1，在Rt△ABC中，∠ABC=60°，AD是斜边BC上的高，沿AD 将△ABC折成60°的二面角B﹣AD﹣C，如图2．（1）证明：平面ABD⊥平面BCD；（2）在图2中，设E为BC的中点，求异面直线AE与BD所成的角．20．（12分）在长方体ABCD﹣A1B1C1D1中，E，F分别是AD，DD1的中点，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后．得到如图所示的几何体ABCD ﹣A1B1C1D1，且这个几何体的体积为．（1）求证：EF∥平面A1BC1；（2）求A1A的长；（3）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．21．（12分）如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．22．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．（Ⅰ）求证：BC⊥A1B；（Ⅱ）若P是线段AC上一点，，AB=BC=2，三棱锥A1﹣PBC的体积为，求的值．2016-2017学年河北省衡水中学高一（下）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．【解答】解：由俯视图可知，原几何体的上底面应该是圆面，由此排除选项A 和选项C．而俯视图内部只有一个虚圆，所以排除B．故选：D．2．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为BC、BB1的中点，则下列直线中与直线EF相交的是（）A．直线AA1B．直线A1B1C．直线A1D1D．直线B1C1【解答】解：根据异面直线的概念可看出直线AA1，A1B1，A1D1都和直线EF为异面直线；B1C1和EF在同一平面内，且这两直线不平行；∴直线B1C1和直线EF相交，即选项D正确．故选：D．3．（5分）在空间中，设m，n为两条不同直线，α，β为两个不同平面，则下列命题正确的是（）A．若m∥α且α∥β，则m∥βB．若α⊥β，m⊂α，n⊂β，则m⊥nC．若m⊥α且α∥β，则m⊥βD．若m不垂直于α，且n⊂α，则m必不垂直于n【解答】解：由m，n为两条不同直线，α，β为两个不同平面，知：在A中，若m∥α且α∥β，则m∥β或m⊂β，故A错误；在B中，若α⊥β，m⊂α，n⊂β，则m与n相交、平行或异面，故B错误；在C中，若m⊥α且α∥β，则由线面垂直的判定定理得m⊥β，故C正确；在D中，若m不垂直于α，且n⊂α，则m有可能垂直于n，故D错误．故选：C．4．（5分）如图，△O'A'B'是水平放置的△OAB的直观图，则△OAB的周长为（）A．B．3C．D．12【解答】解：根据斜二侧画法得到三角形OAB为直角三角形，底面边长0B=4，高OA=2O'A'=6，AB=2，∴直角三角形OAB的周长为10+2．故选：A．5．（5分）若正四棱锥的侧棱长为，侧面与底面所成的角是45°，则该正四棱锥的体积是（）A．B．C．D．【解答】解：过棱锥定点S作SE⊥AD，SO⊥平面ABCD，则E为AD的中点，O 为正方形ABCD的中心．连结OE，则∠SEO为侧面SAD与底面ABCD所成角的平面角，即∠SEO=45°．设正四棱锥的底面边长为a，则AE=OE=SO=，∴SE==．在Rt△SAE中，∵SA2=AE2+SE2，∴3=，解得a=2．∴SO=1，∴棱锥的体积V==．故选：B．6．（5分）已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O﹣ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）A．B．4πC．D．3π【解答】解：设正△ABC的中心为O1，连结O1O、O1C、O1D、OD，∵O1是正△ABC的中心，A、B、C三点都在球面上，∴O1O⊥平面ABC，结合O1C⊂平面ABC，可得O1O⊥O1C，∵球的半径R=3，O1O=2，∴Rt△O1OC中，O1C=．又∵D为BC的中点，∴Rt△O1DC中，O1D=O1C=．∴Rt△OO1D中，OD==．∵过D作球O的截面，当截面与OD垂直时，截面圆的半径最小，∴当截面与OD垂直时，截面圆的面积有最小值．此时截面圆的半径r==，可得截面面积为S=πr2=．故选：A．7．（5分）若某空间几何体的三视图如图所示，则该几何体的表面积是（）A．48+πB．48﹣πC．48+2πD．48﹣2π【解答】解：由三视图可知，原几何体为底面边长是2，高是5的正四棱柱内部挖去一个半径为1的半球．其表面积为=48+π．故选：A．8．（5分）已知棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设面MEF∩面MPQ=l，则下列结论中不成立的是（）A．l∥面ABCDB．l⊥ACC．面MEF与面MPQ不垂直D．当x变化时，l不是定直线【解答】解：如图作出过M的中截面，∵棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，QP∥EF，EF∥中截面，由平面与平面平行的性质定理，可知：面MEF∩面MPQ=l，由平面与平面平行的性质定理可知：l∥面ABCD；∵几何体是正方体，∴AC⊥EF，由三垂线定理可知：l⊥AC．过ACC1A1的平面如图，面MEF与面MPQ不垂直，当Q、P与D1，B1重合时，面MEF与面MPQ垂直，直线l与EF平行，是定直线．D错误．故选：D．9．（5分）已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（）A．B．C．3πD．4π【解答】解：由三视图可知，该几何体是一个三棱锥，如图所示，则几何体的表面积为，该几何体的体积为；设其内切球半径为r，则，求得，所以内切球的表面积为．故选：B．10．（5分）如图，等边△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，下列命题中，错误的是（）A．动点A′在平面ABC上的射影在线段AF上B．恒有平面A′GF⊥平面BCEDC．三棱锥A′﹣EFD的体积有最大值D．异面直线A′E与BD不可能垂直【解答】解：∵A′D=A′E，△ABC是正三角形，∴A′在平面ABC上的射影在线段AF上，故A正确；由A知，平面A′GF一定过平面BCED的垂线，∴恒有平面A′GF⊥平面BCED，故B正确；三棱锥A′﹣FED的底面积是定值，体积由高即A′到底面的距离决定，当平面A′DE⊥平面BCED时，三棱锥A′﹣FED的体积有最大值，故C正确；当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④错误．故选：D．11．（5分）已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的体积为V=，则OA与平面ABCD所成的角的余弦值为（）球A．B．C．D．【解答】解：如图，设球O的半径为R，由V==，球得，∴R=，即OA=．设正方形ABCD的中心为G，连接OG，则OG⊥平面ABCD，且AG=．∴OA与平面ABCD所成的角的余弦值为．故选：A．12．（5分）在底面为正三角形的直棱柱（侧棱垂直于底面的棱柱）ABC﹣A1B1C1中，AB=2，AA1=3，点D为棱BD的中点，点E为A，C上的点，且满足A1E=mEC （m∈R），当二面角E﹣AD﹣C的余弦值为时，实数m的值为（）A．1B．2C．D．3【解答】解：在正三棱柱ABC﹣A1B1C1中，取AC中点O，以O为坐标原点，以OB、OC所在直线为x、y轴建立如图所示空间直角坐标系，∵AB=2，AA1=3，点D为棱BC的中点，∴A（0，﹣1，0），C（0，1，0），D（），A1（0，﹣1，3），又点E为A1C上的点，且满足A1E=mEC（m∈R），∴，设E（x，y，z），则，，∴（x，y+1，z﹣3）=（﹣mx，m﹣my，﹣mz），得x=0，y=，z=．∴E（0，，），则，，设平面AED的一个法向量为，由，取x=，得．平面ADC的一个法向量．∴|cos＜＞|=||=||=．解得：m=1．故选：A．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点A到平面A1DB的距离为．【解答】解：构造三棱锥A﹣A 1DB，并且有=，因为=sh=××1×1×1=，所以==．设点A到平面A1DB的距离为x，又因为=×S A1BD×x=×××x=，所以x=，即点A到平面A1DB的距离为．故答案为：14．（5分）在三棱锥A﹣BCD中，侧棱AB，AC，AD两两垂直，△ABC、△ACD、△ABD的面积分别为、、，则三棱锥A﹣BCD的外接球的体积为8π．【解答】解：三棱锥A﹣BCD中，侧棱AB、AC、AD两两垂直，补成长方体，两者的外接球是同一个，长方体的对角线就是球的直径，设长方体的三边为a，b，c，则由题意得：ab=4，ac=4，bc=4，解得：a=2，b=2，c=2，所以球的直径为：=2所以球的半径为，所以三棱锥A﹣BCD的外接球的体积为=8π故答案为：8π．15．（5分）如图，三棱锥A﹣BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是．【解答】解：如图，取BC中点O，在△ABC和△BCD中，∵CA=AB=BC=CD=DB=4，∴AO=DO=2，在△AOD中，AO=DO=2，又AD=2，∴cos∠AOD===0，则∠AOD=，∴将该三棱锥以BC为轴转动，到点A落到平面α内时，A、D两点所经过的路程都是以O为圆心，以OA为半径的圆周，∴A、D两点所经过的路程之和是×2π×OA=．故答案为：．16．（5分）在正方体ABCD﹣A1B1C1D1中（如图），已知点P在直线BC1上运动．则下列四个命题：①三棱锥A﹣D1BC的体积不变；②直线AP与平面ACD1所成的角的大小不变；③二面角P﹣AD1﹣C的大小不变；④M是平面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是直线A1D1其中正确命题的编号是①③④．（写出所有正确命题的编号）【解答】解：对于①，显然三棱锥A﹣D1BC体积与P点位置无关，故①正确；对于②，以D1为坐标原点，建立如图所示的空间坐标系，设正方体边长为1，则=（1，1，﹣1）为平面ACD1的法向量，而=（1，0，0），=（1，﹣1，﹣1），∴cos＜＞==，cos＜，＞==，∴AB，AC1与平面ACD1所成的角不相等，即当p在直线BC1上运动时，AP平面ACD1所成的角会发生变化，故②错误；对于③，当P位置变化时，平面PAD1的位置不发生变化，故二面角P﹣AD1﹣C 的大小不变，故③正确；对于④，设Q为直线A1D1上任意一点，则Rt△QDD1≌Rt△QC1D1，∴QD=QC1，∴M的轨迹为直线A1D1，故④正确．故答案为：①③④．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10分）如图，O是圆锥底面圆的圆心，圆锥的轴截面PAB为等腰直角三角形，C为底面圆周上一点．（Ⅰ）若弧的中点为D，求证：AC∥平面POD（Ⅱ）如果△PAB面积是9，求此圆锥的表面积与体积．【解答】（Ⅰ）证明：∵AB是底面圆的直径，∴AC⊥BC．∵的中点为D，∴OD⊥BC．又AC、OD共面，∴AC∥OD．又AC⊄平面POD，OD⊂平面POD，∴AC∥平面POD；（Ⅱ）解：设圆锥底面圆半径为r，高为h，母线长为l，∵圆锥的轴截面PAB为等腰直角三角形，∴h=r，l=，由，得r=3，∴，．18．（12分）《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形，且侧棱与底面垂直的棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABM﹣DCP与刍童的组合体中AB=AD，A1B1=A1D1．棱台体积公式：V=（S′++S）h，其中S′，S分别为棱台上、下底面面积，h为棱台高．（Ⅰ）证明：直线BD⊥平面MAC；（Ⅱ）若AB=1，A1D1=2，MA=，三棱锥A﹣A1B1D1的体积V=，求该组合体的体积．【解答】解：（Ⅰ）证明：由题可知ABM﹣DCP是底面为直角三角形的直棱柱，∴AD⊥平面MAB，又MA⊂平面MAB，∴AD⊥MA，又MA⊥AB，AD∩AB=A，AD，AB⊂平面ABCD，∴MA⊥平面ABCD，又BD⊂平面ABCD，∴MA⊥BD．又AB=AD，∴四边形ABCD为正方形，∴BD⊥AC，又MA∩AC=A，MA，AC⊂平面MAC，∴BD⊥平面MAC．…（6分）（Ⅱ）设刍童ABCD﹣A1B1C1D1的高为h，则三棱锥A﹣A1B1D1体积V==，∴h=，故该组合体的体积为V==．19．（12分）如图1，在Rt△ABC中，∠ABC=60°，AD是斜边BC上的高，沿AD 将△ABC折成60°的二面角B﹣AD﹣C，如图2．（1）证明：平面ABD⊥平面BCD；（2）在图2中，设E为BC的中点，求异面直线AE与BD所成的角．【解答】证明：（1）∵折起前AD是BC边上的高，∴当折起后，AD⊥CD，AD⊥BD，又CD∩BD=D，∴AD⊥平面BCD，∵AD⊂平面ABD，∴平面ABD⊥平面BCD．解：（2）取CD的中点F，连结EF，由EF∥BD，∴∠AEF是异面直线AE与BD所成角，连结AF、DE，设BD=2，则EF=1，AD=2，CD=6，DF=3，在Rt△ADF中，AF==，在△BCD中，由题设知∠BDC=60°，则BC2=BD2+CD2﹣2BD•CD•cos60°=28，∴BC=2，∴BE=，∴cos，在△BDE中，DE2=BD2+BE2﹣2BD•BE•cos∠CBD=13，在Rt△ADE中，cos∠AEF===，∴∠AEF=60°，'∴异面直线AE与BD所成的角为60°．20．（12分）在长方体ABCD﹣A1B1C1D1中，E，F分别是AD，DD1的中点，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后．得到如图所示的几何体ABCD﹣A1B1C1D1，且这个几何体的体积为．（1）求证：EF∥平面A1BC1；（2）求A1A的长；（3）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．【解答】证明：（1）如图，连接AD1，∵E，F分别是AD，DD1的中点，∴AD1∥EF．又∵AD1∥BC1，∴EF∥BC1，∵EF⊄平面A1BC1，BC1⊂平面A1BC1，∴EF∥平面A1BC1解：（2）设A1A=h，∵几何体ABCD﹣A1C1D1的体积为，=V ABCD﹣A1B1C1D1﹣V B﹣A1B1C1=，∴V ABCD﹣A1C1D1即S ABCD×h﹣×S△A1B1C1×h=，即2×2×h﹣××2×2×h=，解得h=4．∴A1A的长为4．（3）在平面CC1D1D中作D1Q⊥C1D交CC1于Q，过Q作QP∥CB交BC1于点P，则A1P⊥C1D．（7分）因为A1D1⊥平面CC1D1D，C1D⊂平面CC1D1D，∴C1D⊥A1D1，而QP∥CB，CB∥A1D1，∴QP∥A1D1，又∵A1D1∩D1Q=D1，∴C1D⊥平面A1PQC1，且A1P⊂平面A1PQC1，∴A1P⊥C1D．（10分）∵△D1C1Q∽Rt△C1CD，∴=，∴C1Q=1又∵PQ∥BC，∴PQ=BC=．∵四边形A1PQD1为直角梯形，且高D1Q=，∴A1P==21．（12分）如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．【解答】（Ⅰ）证明：在直角梯形ABCD中，∵AB∥CD，BC⊥CD，AB=BC=2，CD=1∴AD==∵侧面SAB为等边三角形，AB=2∴SA=2∵SD=1∴AD2=SA2+SD2∴SD⊥SA同理：SD⊥SB∵SA∩SB=S，SA，SB⊂面SAB∴SD⊥平面SAB（Ⅱ）建立如图所示的空间坐标系则A（2，﹣1，0），B（2，1，0），C（0，1，0），作出S在底面上的投影M，则由四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB 为等边三角形知，M点一定在x轴上，又AB=BC=2，CD=SD=1．可解得MD=，从而解得SM=，故可得S（，0，）则设平面SBC的一个法向量为则，即取x=0，y=，z=1即平面SBC的一个法向量为=（0，，1）又=（0，2，0）cos＜，＞===∴＜，＞=arccos即AB与平面SBC所成的角的大小为arcsin22．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．（Ⅰ）求证：BC⊥A1B；（Ⅱ）若P是线段AC上一点，，AB=BC=2，三棱锥A1﹣PBC的体积为，求的值．【解答】（Ⅰ）证明∵AD⊥平面A1BC，BC⊂平面A1BC，∴AD⊥BC．∵AA1⊥平面ABC，BC⊂平面ABC，∴AA1⊥BC．又∵AA1∩AD=A，AA1⊂平面AA1B，AD⊂平面AA1B，∴BC⊥平面AA1B，∵A1B⊂平面AA1B，∴BC⊥A1B．（Ⅱ）解：设PC=x，过点B作BE⊥AC于点E．由（Ⅰ）知BC⊥平面AA1B1B，∴BC⊥AB，∵AB=BC=2，∴，．∴，∵AD⊥平面A1BC，其垂足D落在直线A1B上，∴AD⊥A1B．∴BD==1，又∵AA1⊥AB，∴Rt△ABD∽Rt△A1BA，∴，∴．∴=．解得：，∴．∴．。

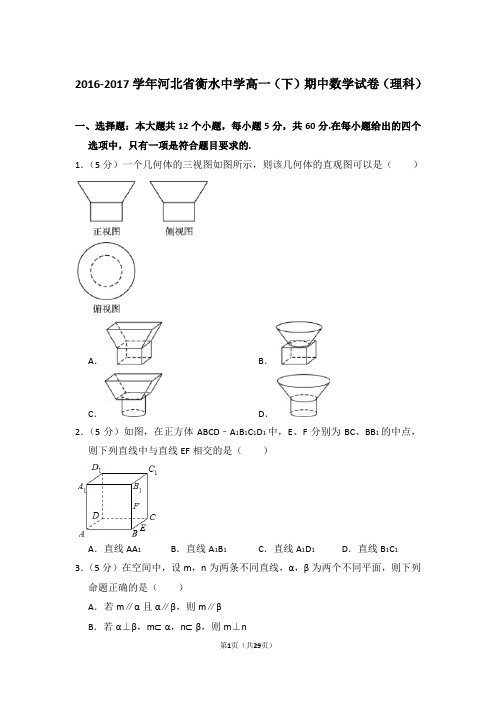
2016-2017学年河北省衡水中学高一（下）期中数学试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．2．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为BC、BB1的中点，则下列直线中与直线EF相交的是（）A．直线AA1B．直线A1B1C．直线A1D1D．直线B1C1 3．（5分）在空间中，设m，n为两条不同直线，α，β为两个不同平面，则下列命题正确的是（）A．若m∥α且α∥β，则m∥βB．若α⊥β，m⊂α，n⊂β，则m⊥nC．若m⊥α且α∥β，则m⊥βD．若m不垂直于α，且n⊂α，则m必不垂直于n4．（5分）如图，△O'A'B'是水平放置的△OAB的直观图，则△OAB的周长为（）A．B．3C．D．125．（5分）若正四棱锥的侧棱长为，侧面与底面所成的角是45°，则该正四棱锥的体积是（）A．B．C．D．6．（5分）已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O﹣ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）A．B．4πC．D．3π7．（5分）若某空间几何体的三视图如图所示，则该几何体的表面积是（）A．48+πB．48﹣πC．48+2πD．48﹣2π8．（5分）已知棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设面MEF∩面MPQ=l，则下列结论中不成立的是（）A．l∥面ABCDB．l⊥ACC．面MEF与面MPQ不垂直D．当x变化时，l不是定直线9．（5分）已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（）A．B．C．3πD．4π10．（5分）如图，等边△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，下列命题中，错误的是（）A．动点A′在平面ABC上的射影在线段AF上B．恒有平面A′GF⊥平面BCEDC．三棱锥A′﹣EFD的体积有最大值D．异面直线A′E与BD不可能垂直11．（5分）已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的=，则OA与平面ABCD所成的角的余弦值为（）体积为V球A．B．C．D．12．（5分）在底面为正三角形的直棱柱（侧棱垂直于底面的棱柱）ABC﹣A1B1C1中，AB=2，AA1=3，点D为棱BD的中点，点E为A，C上的点，且满足A1E=mEC （m∈R），当二面角E﹣AD﹣C的余弦值为时，实数m的值为（）A．1B．2C．D．3二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点A到平面A1DB的距离为．14．（5分）在三棱锥A﹣BCD中，侧棱AB，AC，AD两两垂直，△ABC、△ACD、△ABD的面积分别为、、，则三棱锥A﹣BCD的外接球的体积为．15．（5分）如图，三棱锥A﹣BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D 两点所经过的路程之和是．16．（5分）在正方体ABCD﹣A1B1C1D1中（如图），已知点P在直线BC1上运动．则下列四个命题：①三棱锥A﹣D1BC的体积不变；②直线AP与平面ACD1所成的角的大小不变；③二面角P﹣AD1﹣C的大小不变；④M是平面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是直线A1D1其中正确命题的编号是．（写出所有正确命题的编号）三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10分）如图，O是圆锥底面圆的圆心，圆锥的轴截面PAB为等腰直角三角形，C为底面圆周上一点．（Ⅰ）若弧的中点为D，求证：AC∥平面POD（Ⅱ）如果△PAB面积是9，求此圆锥的表面积与体积．18．（12分）《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形，且侧棱与底面垂直的棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABM﹣DCP与刍童的组合体中AB=AD，A1B1=A1D1．棱台体积公式：V=（S′++S）h，其中S′，S分别为棱台上、下底面面积，h为棱台高．（Ⅰ）证明：直线BD⊥平面MAC；（Ⅱ）若AB=1，A1D1=2，MA=，三棱锥A﹣A1B1D1的体积V=，求该组合体的体积．19．（12分）如图1，在Rt△ABC中，∠ABC=60°，AD是斜边BC上的高，沿AD 将△ABC折成60°的二面角B﹣AD﹣C，如图2．（1）证明：平面ABD⊥平面BCD；（2）在图2中，设E为BC的中点，求异面直线AE与BD所成的角．20．（12分）在长方体ABCD﹣A1B1C1D1中，E，F分别是AD，DD1的中点，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后．得到如图所示的几何体ABCD ﹣A1B1C1D1，且这个几何体的体积为．（1）求证：EF∥平面A1BC1；（2）求A1A的长；（3）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．21．（12分）如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．22．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．（Ⅰ）求证：BC⊥A1B；（Ⅱ）若P是线段AC上一点，，AB=BC=2，三棱锥A1﹣PBC的体积为，求的值．2016-2017学年河北省衡水中学高一（下）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．【解答】解：由俯视图可知，原几何体的上底面应该是圆面，由此排除选项A 和选项C．而俯视图内部只有一个虚圆，所以排除B．故选：D．2．（5分）如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为BC、BB1的中点，则下列直线中与直线EF相交的是（）A．直线AA1B．直线A1B1C．直线A1D1D．直线B1C1【解答】解：根据异面直线的概念可看出直线AA1，A1B1，A1D1都和直线EF为异面直线；B1C1和EF在同一平面内，且这两直线不平行；∴直线B1C1和直线EF相交，即选项D正确．故选：D．3．（5分）在空间中，设m，n为两条不同直线，α，β为两个不同平面，则下列命题正确的是（）A．若m∥α且α∥β，则m∥βB．若α⊥β，m⊂α，n⊂β，则m⊥nC．若m⊥α且α∥β，则m⊥βD．若m不垂直于α，且n⊂α，则m必不垂直于n【解答】解：由m，n为两条不同直线，α，β为两个不同平面，知：在A中，若m∥α且α∥β，则m∥β或m⊂β，故A错误；在B中，若α⊥β，m⊂α，n⊂β，则m与n相交、平行或异面，故B错误；在C中，若m⊥α且α∥β，则由线面垂直的判定定理得m⊥β，故C正确；在D中，若m不垂直于α，且n⊂α，则m有可能垂直于n，故D错误．故选：C．4．（5分）如图，△O'A'B'是水平放置的△OAB的直观图，则△OAB的周长为（）A．B．3C．D．12【解答】解：根据斜二侧画法得到三角形OAB为直角三角形，底面边长0B=4，高OA=2O'A'=6，AB=2，∴直角三角形OAB的周长为10+2．故选：A．5．（5分）若正四棱锥的侧棱长为，侧面与底面所成的角是45°，则该正四棱锥的体积是（）A．B．C．D．【解答】解：过棱锥定点S作SE⊥AD，SO⊥平面ABCD，则E为AD的中点，O 为正方形ABCD的中心．连结OE，则∠SEO为侧面SAD与底面ABCD所成角的平面角，即∠SEO=45°．设正四棱锥的底面边长为a，则AE=OE=SO=，∴SE==．在Rt△SAE中，∵SA2=AE2+SE2，∴3=，解得a=2．∴SO=1，∴棱锥的体积V==．故选：B．6．（5分）已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O﹣ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）A．B．4πC．D．3π【解答】解：设正△ABC的中心为O1，连结O1O、O1C、O1D、OD，∵O1是正△ABC的中心，A、B、C三点都在球面上，∴O1O⊥平面ABC，结合O1C⊂平面ABC，可得O1O⊥O1C，∵球的半径R=3，O1O=2，∴Rt△O1OC中，O1C=．又∵D为BC的中点，∴Rt△O1DC中，O1D=O1C=．∴Rt△OO1D中，OD==．∵过D作球O的截面，当截面与OD垂直时，截面圆的半径最小，∴当截面与OD垂直时，截面圆的面积有最小值．此时截面圆的半径r==，可得截面面积为S=πr2=．故选：A．7．（5分）若某空间几何体的三视图如图所示，则该几何体的表面积是（）A．48+πB．48﹣πC．48+2πD．48﹣2π【解答】解：由三视图可知，原几何体为底面边长是2，高是5的正四棱柱内部挖去一个半径为1的半球．其表面积为=48+π．故选：A．8．（5分）已知棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设面MEF∩面MPQ=l，则下列结论中不成立的是（）A．l∥面ABCDB．l⊥ACC．面MEF与面MPQ不垂直D．当x变化时，l不是定直线【解答】解：如图作出过M的中截面，∵棱长为1的正方体ABCD﹣A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，QP∥EF，EF∥中截面，由平面与平面平行的性质定理，可知：面MEF∩面MPQ=l，由平面与平面平行的性质定理可知：l∥面ABCD；∵几何体是正方体，∴AC⊥EF，由三垂线定理可知：l⊥AC．过ACC1A1的平面如图，面MEF与面MPQ不垂直，当Q、P与D1，B1重合时，面MEF与面MPQ垂直，直线l与EF平行，是定直线．D错误．9．（5分）已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（）A．B．C．3πD．4π【解答】解：由三视图可知，该几何体是一个三棱锥，如图所示，则几何体的表面积为，该几何体的体积为；设其内切球半径为r，则，求得，所以内切球的表面积为．10．（5分）如图，等边△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，下列命题中，错误的是（）A．动点A′在平面ABC上的射影在线段AF上B．恒有平面A′GF⊥平面BCEDC．三棱锥A′﹣EFD的体积有最大值D．异面直线A′E与BD不可能垂直【解答】解：∵A′D=A′E，△ABC是正三角形，∴A′在平面ABC上的射影在线段AF上，故A正确；由A知，平面A′GF一定过平面BCED的垂线，∴恒有平面A′GF⊥平面BCED，故B正确；三棱锥A′﹣FED的底面积是定值，体积由高即A′到底面的距离决定，当平面A′DE⊥平面BCED时，三棱锥A′﹣FED的体积有最大值，故C正确；当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④错误．故选：D．11．（5分）已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的体积为V=，则OA与平面ABCD所成的角的余弦值为（）球A．B．C．D．【解答】解：如图，==，设球O的半径为R，由V球得，∴R=，即OA=．设正方形ABCD的中心为G，连接OG，则OG⊥平面ABCD，且AG=．∴OA与平面ABCD所成的角的余弦值为．故选：A．12．（5分）在底面为正三角形的直棱柱（侧棱垂直于底面的棱柱）ABC﹣A1B1C1中，AB=2，AA1=3，点D为棱BD的中点，点E为A，C上的点，且满足A1E=mEC （m∈R），当二面角E﹣AD﹣C的余弦值为时，实数m的值为（）A．1B．2C．D．3【解答】解：在正三棱柱ABC﹣A1B1C1中，取AC中点O，以O为坐标原点，以OB、OC所在直线为x、y轴建立如图所示空间直角坐标系，∵AB=2，AA1=3，点D为棱BC的中点，∴A（0，﹣1，0），C（0，1，0），D（），A1（0，﹣1，3），又点E为A1C上的点，且满足A1E=mEC（m∈R），∴，设E（x，y，z），则，，∴（x，y+1，z﹣3）=（﹣mx，m﹣my，﹣mz），得x=0，y=，z=．∴E（0，，），则，，设平面AED的一个法向量为，由，取x=，得．平面ADC的一个法向量．∴|cos＜＞|=||=||=．解得：m=1．故选：A．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）在棱长为1的正方体ABCD﹣A1B1C1D1中，点A到平面A1DB的距离为．【解答】解：构造三棱锥A﹣A 1DB，并且有=，因为=sh=××1×1×1=，所以==．设点A到平面A1DB的距离为x，又因为=×S A1BD×x=×××x=，所以x=，即点A到平面A1DB的距离为．故答案为：14．（5分）在三棱锥A﹣BCD中，侧棱AB，AC，AD两两垂直，△ABC、△ACD、△ABD的面积分别为、、，则三棱锥A﹣BCD的外接球的体积为8π．【解答】解：三棱锥A﹣BCD中，侧棱AB、AC、AD两两垂直，补成长方体，两者的外接球是同一个，长方体的对角线就是球的直径，设长方体的三边为a，b，c，则由题意得：ab=4，ac=4，bc=4，解得：a=2，b=2，c=2，所以球的直径为：=2所以球的半径为，所以三棱锥A﹣BCD的外接球的体积为=8π故答案为：8π．15．（5分）如图，三棱锥A﹣BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=4，AD=2，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是．【解答】解：如图，取BC中点O，在△ABC和△BCD中，∵CA=AB=BC=CD=DB=4，∴AO=DO=2，在△AOD中，AO=DO=2，又AD=2，∴cos∠AOD===0，则∠AOD=，∴将该三棱锥以BC为轴转动，到点A落到平面α内时，A、D两点所经过的路程都是以O为圆心，以OA为半径的圆周，∴A、D两点所经过的路程之和是×2π×OA=．故答案为：．16．（5分）在正方体ABCD﹣A1B1C1D1中（如图），已知点P在直线BC1上运动．则下列四个命题：①三棱锥A﹣D1BC的体积不变；②直线AP与平面ACD1所成的角的大小不变；③二面角P﹣AD1﹣C的大小不变；④M是平面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是直线A1D1其中正确命题的编号是①③④．（写出所有正确命题的编号）【解答】解：对于①，显然三棱锥A﹣D1BC体积与P点位置无关，故①正确；对于②，以D1为坐标原点，建立如图所示的空间坐标系，设正方体边长为1，则=（1，1，﹣1）为平面ACD1的法向量，而=（1，0，0），=（1，﹣1，﹣1），∴cos＜＞==，cos＜，＞==，∴AB，AC1与平面ACD1所成的角不相等，即当p在直线BC1上运动时，AP平面ACD1所成的角会发生变化，故②错误；对于③，当P位置变化时，平面PAD1的位置不发生变化，故二面角P﹣AD1﹣C 的大小不变，故③正确；对于④，设Q为直线A1D1上任意一点，则Rt△QDD1≌Rt△QC1D1，∴QD=QC1，∴M的轨迹为直线A1D1，故④正确．故答案为：①③④．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（10分）如图，O是圆锥底面圆的圆心，圆锥的轴截面PAB为等腰直角三角形，C为底面圆周上一点．（Ⅰ）若弧的中点为D，求证：AC∥平面POD（Ⅱ）如果△PAB面积是9，求此圆锥的表面积与体积．【解答】（Ⅰ）证明：∵AB是底面圆的直径，∴AC⊥BC．∵的中点为D，∴OD⊥BC．又AC、OD共面，∴AC∥OD．又AC⊄平面POD，OD⊂平面POD，∴AC∥平面POD；（Ⅱ）解：设圆锥底面圆半径为r，高为h，母线长为l，∵圆锥的轴截面PAB为等腰直角三角形，∴h=r，l=，由，得r=3，∴，．18．（12分）《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形，且侧棱与底面垂直的棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABM﹣DCP与刍童的组合体中AB=AD，A1B1=A1D1．棱台体积公式：V=（S′++S）h，其中S′，S分别为棱台上、下底面面积，h为棱台高．（Ⅰ）证明：直线BD⊥平面MAC；（Ⅱ）若AB=1，A1D1=2，MA=，三棱锥A﹣A1B1D1的体积V=，求该组合体的体积．【解答】解：（Ⅰ）证明：由题可知ABM﹣DCP是底面为直角三角形的直棱柱，∴AD⊥平面MAB，又MA⊂平面MAB，∴AD⊥MA，又MA⊥AB，AD∩AB=A，AD，AB⊂平面ABCD，∴MA⊥平面ABCD，又BD⊂平面ABCD，∴MA⊥BD．又AB=AD，∴四边形ABCD为正方形，∴BD⊥AC，又MA∩AC=A，MA，AC⊂平面MAC，∴BD⊥平面MAC．…（6分）（Ⅱ）设刍童ABCD﹣A1B1C1D1的高为h，则三棱锥A﹣A1B1D1体积V==，∴h=，故该组合体的体积为V==．19．（12分）如图1，在Rt△ABC中，∠ABC=60°，AD是斜边BC上的高，沿AD 将△ABC折成60°的二面角B﹣AD﹣C，如图2．（1）证明：平面ABD⊥平面BCD；（2）在图2中，设E为BC的中点，求异面直线AE与BD所成的角．【解答】证明：（1）∵折起前AD是BC边上的高，∴当折起后，AD⊥CD，AD⊥BD，又CD∩BD=D，∴AD⊥平面BCD，∵AD⊂平面ABD，∴平面ABD⊥平面BCD．解：（2）取CD的中点F，连结EF，由EF∥BD，∴∠AEF是异面直线AE与BD所成角，连结AF、DE，设BD=2，则EF=1，AD=2，CD=6，DF=3，在Rt△ADF中，AF==，在△BCD中，由题设知∠BDC=60°，则BC2=BD2+CD2﹣2BD•CD•cos60°=28，∴BC=2，∴BE=，∴cos，在△BDE中，DE2=BD2+BE2﹣2BD•BE•cos∠CBD=13，在Rt△ADE中，cos∠AEF===，∴∠AEF=60°，'∴异面直线AE与BD所成的角为60°．20．（12分）在长方体ABCD﹣A1B1C1D1中，E，F分别是AD，DD1的中点，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后．得到如图所示的几何体ABCD ﹣A1B1C1D1，且这个几何体的体积为．（1）求证：EF∥平面A1BC1；（2）求A1A的长；（3）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．【解答】证明：（1）如图，连接AD1，∵E，F分别是AD，DD1的中点，∴AD1∥EF．又∵AD1∥BC1，∴EF∥BC1，∵EF⊄平面A1BC1，BC1⊂平面A1BC1，∴EF∥平面A1BC1解：（2）设A1A=h，∵几何体ABCD﹣A1C1D1的体积为，∴V ABCD=V ABCD﹣A1B1C1D1﹣V B﹣A1B1C1=，﹣A1C1D1即S ABCD×h﹣×S△A1B1C1×h=，即2×2×h﹣××2×2×h=，解得h=4．∴A1A的长为4．（3）在平面CC1D1D中作D1Q⊥C1D交CC1于Q，过Q作QP∥CB交BC1于点P，则A1P⊥C1D．（7分）因为A1D1⊥平面CC1D1D，C1D⊂平面CC1D1D，∴C1D⊥A1D1，而QP∥CB，CB∥A1D1，∴QP∥A1D1，又∵A1D1∩D1Q=D1，∴C1D⊥平面A1PQC1，且A1P⊂平面A1PQC1，∴A1P⊥C1D．（10分）∵△D1C1Q∽Rt△C1CD，∴=，∴C1Q=1又∵PQ∥BC，∴PQ=BC=．∵四边形A1PQD1为直角梯形，且高D1Q=，∴A1P==21．（12分）如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．【解答】（Ⅰ）证明：在直角梯形ABCD中，∵AB∥CD，BC⊥CD，AB=BC=2，CD=1∴AD==∵侧面SAB为等边三角形，AB=2∴SA=2∵SD=1∴AD2=SA2+SD2∴SD⊥SA同理：SD⊥SB∵SA∩SB=S，SA，SB⊂面SAB∴SD⊥平面SAB（Ⅱ）建立如图所示的空间坐标系则A（2，﹣1，0），B（2，1，0），C（0，1，0），作出S在底面上的投影M，则由四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB 为等边三角形知，M点一定在x轴上，又AB=BC=2，CD=SD=1．可解得MD=，从而解得SM=，故可得S（，0，）则设平面SBC的一个法向量为则，即取x=0，y=，z=1即平面SBC的一个法向量为=（0，，1）又=（0，2，0）cos＜，＞===∴＜，＞=arccos即AB与平面SBC所成的角的大小为arcsin22．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上．（Ⅰ）求证：BC⊥A1B；（Ⅱ）若P是线段AC上一点，，AB=BC=2，三棱锥A1﹣PBC的体积为，求的值．【解答】（Ⅰ）证明∵AD⊥平面A1BC，BC⊂平面A1BC，∴AD⊥BC．∵AA1⊥平面ABC，BC⊂平面ABC，∴AA1⊥BC．又∵AA1∩AD=A，AA1⊂平面AA1B，AD⊂平面AA1B，∴BC⊥平面AA1B，∵A1B⊂平面AA1B，∴BC⊥A1B．（Ⅱ）解：设PC=x，过点B作BE⊥AC于点E．由（Ⅰ）知BC⊥平面AA1B1B，∴BC⊥AB，∵AB=BC=2，∴，．∴，∵AD⊥平面A1BC，其垂足D落在直线A1B上，∴AD⊥A1B．∴BD==1，又∵AA1⊥AB，∴Rt△ABD∽Rt△A1BA，∴，∴．∴=．解得：，∴．∴．附赠模型一：手拉手模型—全等等边三角形条件：△OAB，△OCD均为等边三角形结论：①△OAC≌△OBD；②∠AEB=60°；③OE平分∠AED（易忘）等腰RT△条件：△OAB ，△OCD 均为等腰直角三角形结论：①△OAC ≌△OBD ；②∠AEB =90°；③OE 平分∠AED （易忘）任意等腰三角形条件：△OAB ，△OCD 均为等腰三角形，且∠AOB =∠COD结论：①△OAC ≌△OBD ；②∠AEB =∠AOB ；③OE 平分∠AED （易忘）模型总结：核心图形如右图，核心条件如下：①OA =OB ，OC =OD ；②∠AOB =∠COD导角核心图形模型二：手拉手模型—相似条件：CD ∥AB ，将△OCD 旋转至右图位置结论：右图 △OCD ∽△OAB ⇔△OAC ∽△OBD ；且延长AC 交BD 于点E 必有∠BEC=∠BOA 非常重要的结论：必须会熟练证明手拉手相似（特殊情况）当∠AOB =90°时，除△OCD ∽△OAB ⇔△OAC ∽△OBD 之外还会隐藏OCD OAOBOC OD AC BD ∠===tan ，满足BD ⊥AC ，若连接AD 、BC ，则必有 2222CD AB BC AD +=+；BD AC S ABCD ⨯=21（对角线互相垂直四边形）。

2016-2017学年河北省衡水中学高一下学期期中考试数学（理）试题一、选择题1．一个几何体的三视图如下图所示，则该几何体的直观图可以是（ ）A.B. C. D.【答案】B【解析】通过三视图的俯视图可知，该几何体是由两个旋转体组成，故选2．在正方体1111ABCD A BC D 中，,E F 分别为1,BC BB 的中点，则下列直线中与直线 EF 相交的是（ ）A.直线1AAB.直线11A BC.直线11A DD.直线11B C 【答案】D【解析】试题分析：根据已满治安的概念可得直线11111,,AA A B A D 都和直线EF 为异面直线，11B C 和EF 在同一个平面内，且这两条直线不平行；所以直线11B C 和EF 相交，故选D.【考点】异面直线的概念与判断.3．在空间中，设，为两条不同直线， ，为两个不同平面，则下列命题正确的是A. 若且，则B. 若，，，则C. 若且，则D. 若不垂直于，且，则必不垂直于【答案】C【解析】对于答案A若且，也有的可能；对于答案B，若，，，也有、相交等位置关系；对于答案D，若不垂直于，且，直线也有不垂直于的可能；因此以上三个答案都不正确。

依据线面垂直的定义可知答案C是正确的，应选答案C。

4．如图，是水平放置的的直观图，则的周长为 ( )A. B. C. D.【答案】A【解析】是水平放置的的直观图，如图所示：所以周长为：，故选A.5．若正四棱锥的侧棱长为，侧面与底面所成的角是，则该正四棱锥的体积是A. B. C. D.【答案】B【解析】设底面边长为，依据题设可得棱锥的高，底面中心到顶点的距离，由勾股定理可得，解之得，所以正四棱锥的体积，故应选答案B。

6．已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥 的高为2，点D是线段BC的中点，过点D作球O的截面，则截面面积O ABC的最小值为（）A.154π B. 4π C. 72πD. 3π【答案】A【解析】如图，设正三角形ABC 的边长为a ，中心为M ，由题设可知3,2OA OM ==，则AM =23a =⇒=D 为圆心12a =其最小值为2min 154S ππ==⎝⎭，应选答案A 。

试卷类型：B卷河北冀州中学2016-2017学年度下学期期末高一年级理科数学试题（考试时间：120分钟分值：150分）第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合则= ( )A. B. C.D.2.设变量x，y满足约束条件则目标函数的最小值为( )A. B. 10 C.6D.173. 在△ABC中，如果sin A＝sin C，B＝30°，角B所对的边长b＝2，则△ABC的面积为( ) A． B. 1 C．2 D．44.已知点A(1,3),B(4,-1),则与同方向的单位向量是（）A. B. C. D.5.已知等差数列中，前项和为，若，则（）A.36B.40C.42D.456.a，b为正实数，若函数f(x)＝ax3＋bx＋ab－1是奇函数，则f(2)的最小值是( )A．2 B．8 C．4 D．167. 若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )A.5B. 4C.6D.98. 函数的图像恒过定点A，若点A在直线上，其中，则的最小值为（）A. B. C.7 D.119.若，则（）A. B. C. D.10.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是()A. B. C.D.111.已知等差数列前n项和为S n，若S13＜0，S12＞0，则在数列中绝对值最小的项为( )A．第5项B．第7项C．第6项D．第8项12.已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为( )A. B. C. D.第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分。

把答案直接答在答题纸上。

试卷类型：A 卷 河北冀州中学2016-2017学年度下学期期末 高二年级理科数学试题（ 考试时间：120分钟 分值：150分）第Ⅰ卷（选择题 共52分）一、选择题：本大题共13小题，每小题4分，共52分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列说法正确的是( )A. x ∀， y R ∈，若0x y +≠，则1x ≠且1y ≠-B. a R ∈，“11a<”是“1a >”的必要不充分条件C. 命题“x R ∃∈，使得2230x x ++<”的否定是“x R ∀∈，都有2230x x ++>”D. “若22am bm <，则a b <”的逆命题为真命题2．设()()12i x yi ++=，其中i 为虚数单位，x ,y 是实数，则2x yi +=( )A. 1B.C.D. 3．设随机变量ξ服从正态分布()0,1N ，若(1)P p ξ>=，则(10)P ξ-<<=( )A.12p + B. 1p - C. 12p - D. 12p - 4．已知m ， n 是两条不同的直线， α， β是两个不同的平面，给出下列四个命题，错误的命题是( )A. 若//m α， //m β， n αβ⋂=，则//m nB. 若αβ⊥， m α⊥， n β⊥，则m n ⊥C. 若αβ⊥， αγ⊥， m βγ⋂=，则m α⊥D. 若//αβ， //m α，则//m β5．设等差数列满足，且，为其前项和，则数列的最大项为A. 23SB. 25S C. 24S D. 26S6．下图是一个算法流程图，则输出的x 值为 A. 95 B. 47 C. 23 D. 117．二项式2nx⎛⎝的展开式中所有二项式系数和为64，则展开式中的常数项为60，则a 的值为 ( ) A. 2 B. 1 C. -1 D. 1±8．设函数()()lnx =-f x x ax (a R ∈)在区间()0,2上有两个极值点，则a 的取值范围是( ) A. 1,02⎛⎫- ⎪⎝⎭B. ln210,4+⎛⎫⎪⎝⎭ C.1,12⎛⎫ ⎪⎝⎭ D. ln211,42+⎛⎫⎪⎝⎭9．若双曲线M ： 22221x y a b-=(0a >， 0b >)的左、右焦点分别是1F ， 2F ，以12F F 为直径的圆与双曲线M 相交于点P ，且116PF =， 212PF =，则双曲线M 的离心率为( ) A.54 B. 43 C. 53D. 5 10．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某四棱锥的三视图，则该四棱锥各个侧面中，最大的侧面面积为( ) A. 2B. C. 3 D. 411．已知函数()22cos 22f x x =-．给出下列命题：①(),R f x ββ∃∈+为奇函数；②30,4πα⎛⎫∃∈ ⎪⎝⎭，()()2f x f x α=+对x R ∈恒成立；③12,x x R ∀∈，若()()122f x f x -=，则12x x -的最小值为4π；④12,x x R ∀∈，若()()120f x f x ==，则()12x x k k Z π-=∈．其中的真命题有( )A. ①②B. ③④C. ②③D. ①④ 12．已知双曲线的左右焦点分别为，过点且垂直于轴的直线与该双曲线的左支交于两点，分别交轴于两点，若的周长为12，则取得最大值时该双曲线的离心率为( )A.B.C.D.13．已知函数，．方程有六个不同的实数解，则的取值范围是( )A.B.C.D.第Ⅱ卷（非选择题，共98分）二、填空题：本大题共4小题，每小题4分，共16分。

试卷类型：B卷河北冀州中学2016-2017学年度下学期期末高一年级理科数学试题（考试时间：120分钟分值：150分）第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合则= ( )A. B. C. D.2.设变量x，y满足约束条件则目标函数的最小值为( )A. B. 10 C. 6 D.173. 在△ABC中，如果sin A＝sin C，B＝30°，角B所对的边长b＝2，则△ABC的面积为( ) A． B. 1 C．2 D．44.已知点A(1,3),B(4,-1),则与同方向的单位向量是（）A. B. C. D.5.已知等差数列中，前项和为，若，则（）A.36B.40C.42D.456.a，b为正实数，若函数f(x)＝ax3＋bx＋ab－1是奇函数，则f(2)的最小值是( )A．2 B．8 C．4 D．167.若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为 ( )A.5B. 4C.6D.98.函数的图像恒过定点A，若点A在直线上，其中，则的最小值为（）A. B. C.7 D.119.若，则（）A.B. C. D.10.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是()A. B. C.D.111.已知等差数列前n项和为S n，若S13＜0，S12＞0，则在数列中绝对值最小的项为( )A．第5项 B．第7项 C．第6项 D．第8项12.已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为 ( )A. B. C. D.第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分。

河北省衡水市冀州中学2016-2017学年高一下学期期末考试数学（理）试题B卷第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合则= ( )A. B. C. D.2.设变量x，y满足约束条件则目标函数的最小值为( )A. B. 10 C. 6 D.173. 在△ABC中，如果sin A＝sin C，B＝30°，角B所对的边长b＝2，则△ABC的面积为( )A B. 1 C．2 D．44.已知点A(1,3),B(4,-1),则与同方向的单位向量是( )A. B. C. D.5.已知等差数列中，前项和为，若，则( )A.36B.40C.42D.456.a，b为正实数，若函数f(x)＝ax3＋bx＋ab－1是奇函数，则f(2)的最小值是( )A．2 B．8 C．4 D．167. 若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )A.5B. 4C.6D.98. 函数的图像恒过定点A，若点A在直线上，其中，则的最小值为（）A. B. C.7 D.119.若，则（）A. B. C. D.10.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )A. B. C. D.111.已知等差数列前n项和为S n，若S13＜0，S12＞0，则在数列中绝对值最小的项为( ) A．第5项B．第7项C．第6项D．第8项12.已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则的值为( )A. B. C. D.第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分.13.已知关于的不等式的解集是．则．14. 在锐角△ABC中，AB＝3，AC＝4，S△ABC＝33，则BC＝________．15.实数x,y满足，则x+y的最小值为_________．16.已知数列中，，则________．三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤。

冀州中学下学期第二次月考试题（理科）第Ⅰ卷一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、直线:1l x y -=与圆22:40C x y x +-=的位置关系是A ．相离B ．相切C ．相交D ．无法确定2、,a b 是两个向量，1,2a b ==且()a b a +⊥，则a 与b 的夹角为A ．030B ．060C ．0120D ．01503、直线20x y +-=与圆22(1)(2)1x y -+-=相交于A 、B 两点，则弦AB =A ．2B ．2C 4、已知3sin(),5παα+=是第四象限的角，则(2)cos απ-= A ．45 B ．45- C ．45± D ．35 5、已知向量(2,3),(1,2)a b ==-，若4ma b +与2a b -共线，则m 的值为A ．12B ．2C ．12-D ．-2 6、平面向量a 与b 的夹角为060,(2,0),1a b ==，则2a b +=等于A ．．4 C ．12 D ．167、已知1sin cos ,(0,)5αααπ+=∈，则tan α= A ．43- B ．34- C ．43 D ．348、把函数sin ()y x x R =∈的图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），再把所得图像上所有向左平行移动3π个单位长度，得到的图象所表示的函数是 A ．sin(2),3y x x R π=-∈ B ．sin(),26x y x R π=+∈ C ．sin(2),3y x x R π=+∈ D ．2sin(2),3y x x R π=+∈9、两圆相交于点(1,3),(,1)A B m -，两圆的圆心均为直线0x y c -+=上，则m c +的值为A ．-1B ．2C ．3D ．010、某几何体的三视图如图所示，则该几何体的体积为A ．123π+B ．136π C ．73π D ．52π 11、点(,)P x y 是直线40(0)kx y k ++=>上动点，,PA PB 是圆22:20C x y y +-=的两条切线，,A B 是切点，若四边形PACB 的最小面积是2，则k 的值为A C ．2 12、已知,,ABC 是单位元上互不相同的三点，且满足AB AC =，则AB AC ⋅的最小值为A ．14-B ．12-C ．34- D ．1-第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上。

2016-2017学年河北省衡水市冀州中学高一（下）第二次月考数学试卷（理科）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．直线l ：x ﹣y=1与圆C ：x 2+y 2﹣4x=0的位置关系是（ ） A ．相离 B ．相切 C ．相交 D ．无法确定2．已知，，若，则与的夹角为（ ）A ．30°B ．60°C ．120°D ．150°3．直线x +y ﹣2=0与圆（x ﹣1）2+（y ﹣2）2=1相交于A ，B 两点，则弦|AB |=（ ）A． B ． C ． D ．4．已知sin （π+α）=，且α是第四象限的角，那么cos （α﹣2π）的值是（ ）A ．B ．﹣C ．±D ．5．已知向量=（2，3），=（﹣1，2），若与共线，则m 的值为（ ）A ．B ．2C ．D ．﹣26．平面向量与的夹角为60°，=（2，0），||=1，则|+2|=（ ）A ．B ．C ．4D ．127．已知，则tanα的值为（ ）A ．﹣或﹣B ．或C ．﹣D ．﹣8．把函数y=sinx （x ∈R ）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得图象上所有向左平行移动个单位长度，得到的图象所表示的函数是（ ）A ．B ．C ．D ．9．两圆相交于点A （1，3）、B （m ，﹣1），两圆的圆心均在直线x ﹣y +c=0上，则m+c的值为（）A．﹣1 B．2 C．3 D．010．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C． D．11．已知点P（x，y）是直线kx+y+4=0（k＞0）上一动点，PA、PB是圆C：x2+y2﹣2y=0的两条切线，A、B为切点，若四边形PACB面积的最小值是2，则k的值是（）A．B．C．2 D．212．已知A，B，C是单位圆上互不相同的三点，且满足||=||，则的最小值为（）A．﹣ B．﹣ C．﹣ D．﹣1二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．.13．圆与圆外切，则m的值．14．已知直线y=ax﹣2和y=（a+2）x+1互相垂直，则实数a等于．15．已知向量的夹角为120°，且，则向量在向量方向上的投影为．16．已知a、b、c为某一直角三角形的三条边长，c为斜边．若点（m，n）在直线ax+by+2c=0上，则m2+n2的最小值是．三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤17．已知向量=（1，2），=（﹣3，4）．（1）求+与﹣的夹角；（2）若⊥（+λ），求实数λ的值．18．已知函数．（I）求函数f（x）的最小正周期；（Ⅱ）求函数f（x）的单调递增区间；（Ⅲ）当时，求函数f（x）的最小值，并求出使y=f（x）取得最小值时相应的x值．19．已知向量=（sinθ，cosθ﹣2sinθ），=（1，2），其中0＜θ＜π．（1）若∥，求sinθ•cosθ的值；（2）若|，求θ的值．20．正三棱柱ABC﹣A1B1C1，BC=BB1=1，D为BC上一点，且满足AD⊥C1D．（1）求证：截面ADC1⊥侧面BC1；（2）求点B到截面ADC1距离；（3）求二面角C﹣AC1﹣D的正弦值．21．已知圆C：x2+y2+Dx+Ey+3=0关于直线x+y﹣1=0对称，圆心C在第四象限，半径为．（Ⅰ）求圆C的方程；（Ⅱ）是否存在直线l与圆C相切，且在x轴上的截距是y轴上的截距的2倍？若存在，求直线l的方程；若不存在，说明理由．22．定义在区间[﹣π，π]上的函数y=f（x）的图象关于直线x=﹣对称，当x∈[﹣，π]时，函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，﹣＜φ＜），其图象如图．（Ⅰ）求函数y=f（x）在[﹣π，π]上的表达式；（Ⅱ）求方程f（x）=的解集．2016-2017学年河北省衡水市冀州中学高一（下）第二次月考数学试卷（理科）参考答案与试题解析一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．直线l：x﹣y=1与圆C：x2+y2﹣4x=0的位置关系是（）A．相离B．相切C．相交D．无法确定【考点】J9：直线与圆的位置关系．【分析】先由条件求得圆心和半径，再利用点到直线的距离公式求得圆心C到直线l的距离d小于半径，可得直线和圆的位置关系．【解答】解：由题意可得，圆C的圆心为C（2，0），半径为2，由于圆心C到直线l的距离d==＜2，所以圆与直线相交，故选C．2．已知，，若，则与的夹角为（）A．30°B．60°C．120° D．150°【考点】9S：数量积表示两个向量的夹角．【分析】首先利用已知的向量垂直得到两个向量的数量积，然后根据数量积公式求夹角．【解答】解：已知，，若，则（+）==0，所以=﹣1，所以与的夹角的余弦值为：，所以向量夹角为120°；故选C3．直线x+y﹣2=0与圆（x﹣1）2+（y﹣2）2=1相交于A，B两点，则弦|AB|=（）A．B．C．D．【考点】J9：直线与圆的位置关系．【分析】利用点到直线的距离公式可得：圆心到直线x﹣y﹣1=0的距离d，即可得出弦长|AB|．【解答】解：由圆（x﹣1）2+（y﹣2）2=1，可得圆心M（1，2），半径r=1．∴圆心到直线x+y﹣2=0的距离d==．∴弦长|AB|=2=2×=．故选：D．4．已知sin（π+α）=，且α是第四象限的角，那么cos（α﹣2π）的值是（）A．B．﹣ C．± D．【考点】GO：运用诱导公式化简求值．【分析】直接利用诱导公式化简已知条件，化简所求表达式，【解答】解：sin（π+α）=，可得sinα=﹣，α是第四象限的角，cosα==．cos（α﹣2π）=cosα=．故选：A．5．已知向量=（2，3），=（﹣1，2），若与共线，则m的值为（）A．B．2 C．D．﹣2【考点】96：平行向量与共线向量；9J：平面向量的坐标运算．【分析】先由向量的坐标运算表示出与，再根据向量共线定理的坐标表示可得答案．【解答】解：由题意可知=m（2，3）+4（﹣1，2）=（2m﹣4，3m+8）=（2，3）﹣2（﹣1，2）=（4，﹣1）∵与共线∴（2m﹣4）×（﹣1）=（3m+8）×4∴m=﹣2故选D．6．平面向量与的夹角为60°，=（2，0），||=1，则|+2|=（）A．B． C．4 D．12【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量的坐标求出向量的模，最后结论要求模，一般要把模平方，知道夹角就可以解决平方过程中的数量积问题，题目最后不要忘记开方．【解答】解：由已知|a|=2，|a+2b|2=a2+4a•b+4b2=4+4×2×1×cos60°+4=12，∴|a+2b|=．故选：B．7．已知，则tanα的值为（）A．﹣或﹣B．或C．﹣ D．﹣【考点】GI：三角函数的化简求值；GG：同角三角函数间的基本关系．【分析】通过sinα+cosα=，求出sinαcosα的值，再给式子添上一个分母1，把1变成角的正弦与余弦的平方和，分子和分母同除以余弦的平方，得到关于正切的方程，根据判断的角的范围求出结果．【解答】解：∵sinα+cosα=，所以2sinαcosα=﹣，∴=﹣，∴∴12tan2α+25tanα+12=0根据得到的角的范围得到tan故选C8．把函数y=sinx（x∈R）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得图象上所有向左平行移动个单位长度，得到的图象所表示的函数是（）A．B．C．D．【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【分析】利用y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：把函数y=sinx（x∈R）的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），可得y=sin2x的图象；再把所得图象上所有向左平行移动个单位长度，得到的图象所表示的函数是y=sin（2x+），故选：D．9．两圆相交于点A（1，3）、B（m，﹣1），两圆的圆心均在直线x﹣y+c=0上，则m+c的值为（）A．﹣1 B．2 C．3 D．0【考点】JA：圆与圆的位置关系及其判定．【分析】根据题意可知，x﹣y+c=0是线段AB的垂直平分线，由垂直得到斜率乘积为﹣1，而直线x﹣y+c=0的斜率为1，所以得到过A和B的直线斜率为1，利用A和B的坐标表示出直线AB的斜率等于1，列出关于m的方程，求出方程的解即可得到m的值，然后利用中点公式和m的值求出线段AB的中点坐标，把中点坐标代入x﹣y+c=0中即可求出c的值，利用m和c的值求出m+c的值即可．【解答】解：由题意可知：直线x﹣y+c=0是线段AB的垂直平分线，又直线x﹣y+c=0 的斜率为1，则=﹣1①，且﹣+c=0②，由①解得m=5，把m=5代入②解得c=﹣2，则m+c=5﹣2=3．故选C10．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C． D．【考点】L!：由三视图求面积、体积．【分析】利用三视图判断直观图的形状，结合三视图的数据，求解几何体的体积即可．【解答】解：由题意可知几何体的形状是放倒的圆柱，底面半径为1，高为2，左侧与一个底面半径为1，高为1的半圆锥组成的组合体，几何体的体积为：=．故选：B．11．已知点P（x，y）是直线kx+y+4=0（k＞0）上一动点，PA、PB是圆C：x2+y2﹣2y=0的两条切线，A、B为切点，若四边形PACB面积的最小值是2，则k的值是（）A．B．C．2 D．2【考点】J7：圆的切线方程．【分析】由圆的方程为求得圆心C，半径r，由“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”，最后利用点到直线的距离求出直线的斜率即可．【解答】解：∵圆的方程为：x2+（y﹣1）2=1，∴圆心C（0，1），半径r=1．根据题意，若四边形面积最小，当圆心与点P的距离最小时，即距离为圆心到直线l的距离最小时，切线长PA，PB最小．切线长为2，∴PA=PB=2，∴圆心到直线l的距离为d=．直线方程为y+4=kx，即kx﹣y﹣4=0，∴=，解得k=±2，∵k＞0，∴所求直线的斜率为：2．故选C．12．已知A，B，C是单位圆上互不相同的三点，且满足||=||，则的最小值为（）A．﹣ B．﹣ C．﹣ D．﹣1【考点】9R：平面向量数量积的运算．【分析】由题意可得，点A在BC的垂直平分线上，不妨设单位圆的圆心为O（0，0），点A（0，1），点B（x1，y1），则点C（﹣x1，y1），x12+y12=1，且﹣1≤y1＜1．根据=2y12﹣2y1，再利用二次函数的性质求得它的最小值．再利用二次函数的性质求得它的最小值．【解答】解：由题意可得，点A在BC的垂直平分线上，不妨设单位圆的圆心为O（0，0），点A（0，1），点B（x1，y1），则点C（﹣x1，y1），﹣1≤y1＜1．∴=（x1，y1﹣1），=（﹣x1，y1﹣1），x12+y12=1．∴•=﹣x12+y12﹣2y1+1=﹣（1﹣y12）+y12﹣2y1+1=2y12﹣2y1，∴当y1=时，取得最小值为﹣，故选：B．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．.13．圆与圆外切，则m的值0或﹣3．【考点】JA：圆与圆的位置关系及其判定．【分析】由题意，圆心距==5，即可求出m的值．【解答】解：由题意，圆心距==5，∴m=0或﹣3，故答案为0或﹣3．14．已知直线y=ax﹣2和y=（a+2）x+1互相垂直，则实数a等于﹣1．【考点】IA：两条直线垂直与倾斜角、斜率的关系．【分析】利用斜率都存在的两直线垂直，斜率之积等于﹣1，解方程求出实数a 的值．【解答】解：∵直线y=ax﹣2和y=（a+2）x+1互相垂直，∴他们的斜率之积等于﹣1，即a×（a+2）=﹣1，∴a=﹣1，故答案为：﹣1．15．已知向量的夹角为120°，且，则向量在向量方向上的投影为．【考点】9R：平面向量数量积的运算．【分析】根据平面向量数量积与向量投影的定义，计算即可．【解答】解：向量的夹角为120°，且，则•=2×3×cos120°=﹣3，∴（2+3）（2+）=4+8•+3=4×22+8×（﹣3）+3×32=19，|2+|===；∴向量在向量方向上的投影为|2+3|cos=|2+3|×==．故答案为：．16．已知a、b、c为某一直角三角形的三条边长，c为斜边．若点（m，n）在直线ax+by+2c=0上，则m2+n2的最小值是4．【考点】IT：点到直线的距离公式．【分析】由直角三角形且c为斜边，根据勾股定理表示出一个关系式，因为所求式子即为原点到已知点距离的平方，而点到直线的距离只有垂线段最短，利用点到直线的距离公式表示出原点到已知直线的距离，把表示出的关系式代入即可求出原点到已知直线的距离，平方即可得到所求式子的最小值．【解答】解：根据题意可知：当（m，n）运动到原点与已知直线作垂线的垂足位置时，m2+n2的值最小，由三角形为直角三角形，且c为斜边，根据勾股定理得：c2=a2+b2，所以原点（0，0）到直线ax+by+2c=0的距离d==2，则m2+n2的最小值为4．故答案为：4．三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤17．已知向量=（1，2），=（﹣3，4）．（1）求+与﹣的夹角；（2）若⊥（+λ），求实数λ的值．【考点】9S：数量积表示两个向量的夹角．【分析】（1）由题意求得+和﹣的坐标，再根据两个向量的夹角公式求得两个向量的夹角的余弦值，可得+与﹣的夹角．（2）由•（+λ）=0，求得λ的值．【解答】解：（1）由题意可得+=（﹣2，6），﹣=（4，﹣2），∴，∴求+与﹣的夹角为．（2）若⊥（+λ），则⊥（+λ）=（1，2）•（1﹣3λ，2+4λ）=1﹣3λ+4+8λ=5λ+5=0，求得λ=﹣1．18．已知函数．（I）求函数f（x）的最小正周期；（Ⅱ）求函数f （x ）的单调递增区间；（Ⅲ）当时，求函数f （x ）的最小值，并求出使y=f （x ）取得最小值时相应的x 值．【考点】H2：正弦函数的图象．【分析】（I ）由条件利用正弦函数的周期性求得函数f （x ）的最小正周期． （Ⅱ）由条件利用正弦函数的单调性求得函数f （x ）的单调递增区间． （Ⅲ）由条件利用正弦函数的定义域和值域求得函数f （x ）的最小值，以及此时相应的x 值．【解答】解：（I ）对于函数，它的最小正周期为．（II）令，求得，即．所以 函数f （x ）的单调递增区间是（k ∈Z ）．（III ）∵，∴，即．所以函数f （x ）的最小值是，此时，．19．已知向量=（sinθ，cosθ﹣2sinθ），=（1，2），其中0＜θ＜π． （1）若∥，求sinθ•cosθ的值；（2）若|，求θ的值．【考点】9R ：平面向量数量积的运算．【分析】（1）根据平面向量的共线定理的坐标表示即可解题．（2）由|，化简得sin2θ+cos2θ=﹣1，再由θ∈（0，π）可解出θ的值．【解答】解：（1）因为，所以2sinθ=cosθ﹣2sinθ，显然cosθ≠0，所以．所以sinθ•cosθ===，（2）因为，所以，所以cos 2θ+sinθcosθ=0，cosθ=0或sinθ=﹣cosθ．又0＜θ＜π，所以或．20．正三棱柱ABC﹣A1B1C1，BC=BB1=1，D为BC上一点，且满足AD⊥C1D．（1）求证：截面ADC1⊥侧面BC1；（2）求点B到截面ADC1距离；（3）求二面角C﹣AC1﹣D的正弦值．【考点】MT：二面角的平面角及求法；LY：平面与平面垂直的判定；MK：点、线、面间的距离计算．【分析】（1）推导出AD⊥CC1，AD⊥C1D，从而AD⊥平面BC1，由此能证明截面ADC1⊥侧面BC1．（2）连结A1C，AC1，交于E，设B到面ADC1的距离为d，由，能求出点B到截面ADC1距离．（3）过C作CF⊥AC1于F，连结EF，推导出∠CEF是二面角C﹣AC1﹣D的平面角，由此能求出二面角C﹣AC1﹣D的正弦值．【解答】证明：（1）∵正三棱柱ABC﹣A1B1C1，BC=BB1=1，D为BC上一点，且满足AD⊥C1D．∴AD⊥CC1，AD⊥C1D，∵CC1∩C1D=C1，∴AD⊥平面BC1，∵AD⊂截面ADC1，∴截面ADC1⊥侧面BC1．解：（2）连结A1C，AC1，交于E，由（1）知AD⊥BC，∵正三棱柱ABC﹣A1B1C1，BC=BB1=1，∴△ABC是正三角形，∴D为BC中点，E为A1C中点，∴ED∥A1B，∴A1B∥面AC1D，设B到面ADC1的距离为d，∵，∴，解得d=，∴点B到截面ADC1距离为．（3）过C作CF⊥AC1于F，连结EF，∵截面ADC1⊥侧面BC1，截面ADC1∩侧面BC1=C1D，∴CF⊥面DAC1，又EF为斜线CF在面ADC1上的射影，∴FE⊥AC1，∴∠CEF是二面角C﹣AC1﹣D的平面角，在Rt△C1CD中，由题意得CF=，∴sin∠CEF==，∴二面角C﹣AC1﹣D的正弦值为．21．已知圆C：x2+y2+Dx+Ey+3=0关于直线x+y﹣1=0对称，圆心C在第四象限，半径为．（Ⅰ）求圆C的方程；（Ⅱ）是否存在直线l与圆C相切，且在x轴上的截距是y轴上的截距的2倍？若存在，求直线l的方程；若不存在，说明理由．【考点】JE：直线和圆的方程的应用．【分析】（Ⅰ）将圆的方程化为标准方程，利用圆关于直线x+y﹣1=0对称，圆心C在第四象限，半径为，建立方程组，即可求圆C的方程；（Ⅱ）分类讨论，设出直线方程，利用直线l与圆C相切，建立方程，即可求出直线l的方程．【解答】解：（Ⅰ）由x2+y2+Dx+Ey+3=0得：∴圆心C，半径，由题意，，解之得，D=﹣4，E=2∴圆C的方程为x2+y2﹣4x+2y+3=0…（Ⅱ）由（Ⅰ）知圆心C（2，﹣1），设直线l在x轴、y轴上的截距分别为2a，a．当a=0时，设直线l的方程为kx﹣y=0，则解得，此时直线l的方程为…当a≠0时，设直线l的方程为即x+2y﹣2a=0，则，∴，此时直线l的方程为…综上，存在四条直线满足题意，其方程为或…22．定义在区间[﹣π，π]上的函数y=f（x）的图象关于直线x=﹣对称，当x∈[﹣，π]时，函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，﹣＜φ＜），其图象如图．（Ⅰ）求函数y=f（x）在[﹣π，π]上的表达式；（Ⅱ）求方程f（x）=的解集．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式；GQ：两角和与差的正弦函数．【分析】（1）观察图象易得当时，：，再由函数y=f（x）的图象关于直线对称求出x∈上的解析式，即可得到函数y=f（x）在的表达式；（2）由（1）函数的解析式是一个分段函数，故分段解方程求方程的解．【解答】解：（1）当时，函数，观察图象易得：A=1，周期为2π，可得ω=1，再将点代入，结合题设可得φ=，即函数，由函数y=f（x）的图象关于直线对称得，时，函数f （x）=﹣sinx．∴．（2）当时，由得，；当时，由得，．∴方程的解集为2017年5月27日。