加热弹性圆板的大振幅自由振动
- 格式:pdf
- 大小:176.63 KB
- 文档页数:5


自激振动●迄今讨论的问题都是自由振动或者受迫振动●存在另一类的扰动,称为自激振动⏹通过例子中二者区别的实质●普通单缸蒸汽发动机⏹活塞完成一个往复运动,可以看成是一个振动⏹维持这一振动的力来自蒸汽,在活塞的两侧交替推动●带失衡圆盘的弹性轴⏹弹性轴承在两个支撑上旋转⏹不平衡质量导致的离心力交替推动圆盘上下运动2●蒸汽发动机是自激振动⏹通过约束飞轮限制活塞运动,阀门将停止,不会有交替的蒸汽力作用在活塞上●盘的运动是普通的受迫振动⏹限制盘的振动,例如轴上靠近盘的两侧装两个球轴承,并把球轴承的外圈附在牢固的基础上,这样就限制了盘的振动,但是转动并未受影响.⏹因为失衡旋转继续,交替力一直保留不会消失3●于是总结出以下区别:⏹在自激振动中,维持运动的交替外力由运动自身产生或者控制;如果运动停止,交替外力将消失⏹在受迫振动中,交替外力与运动相互独立,即使运动停止,交替外力仍然存在4另一种看待此问题的方法是把自激振动定义成带有负阻尼的自由振动5●如下的含负阻尼的单自由度运动微分方程:其解可以写为是一个振幅呈指数增加的振动●普通的正阻尼力正比于振动速度并与其方向相反●负阻尼力也与速度成比例,但是与振动方向相同⏹负阻尼不仅没有减少自由振动的振幅,反而使其增加●不管是正阻尼还是负阻尼,都会随着运动停止而消失6●系统的动态稳定性质⏹具有正阻尼:动态稳定⏹具有负阻尼:动态不稳定●系统的静稳定性质⏹静态稳定:从平衡位置开始的位移所形成的力或力偶倾向于驱动系统回到平衡位置⏹静不稳定:这样形成的力倾向于增加位移⏹静不稳定性意味着负的弹性常数,或者更一般地说,其中一个固有频率的值为负●动态稳定和静态稳定的区别⏹动稳定性总是以静稳定性为前提的⏹反过来是不成立的:静态稳定的系统也可以是动不稳定的7系统的三个不同的稳定性阶段的行为(a) 静不稳定; (b) 静稳定,动不稳定; (c) 静稳定且动稳定8自激振动的频率●在大多数的实际例子中,负阻尼相对于运动的弹性力和惯性力很小⏹如果阻尼力为零,振动频率就是固有频率⏹不管是正的阻尼力还是负的阻尼力, 阻尼力将或多或少降低系统的固有频率⏹在机械工程的实践中,这一频率上的区别可以忽略不计,所以自激振动的频率就是系统的固有频率●只有当负阻尼力大于弹性力或者惯性力的时候,自激振动的频率才会与固有频率显著不同9●从能量角度考虑⏹对于正阻尼情况阻尼力做负功,总是与速度反向机械能转变成热能(通常耗散在阻尼器的油里面)这些能量来源于振动系统接下来每次振动振幅减小,动能减小,损失的动能被阻尼力吸收⏹负阻尼的情况阻尼力作为驱动力做正功,在一个循环里面,该功转化成动能,使振动增加●如果没有外来能源(如蒸汽锅炉), 自激振动就不能存在⏹能源自身是没有运动的交替频率的10●对于一个线性自激振动系统,由于每个循环都有能量进入系统里来,其振幅会随时间发展为无限大⏹实际观测不到无限大振幅●在大多数的系统里面,自激振动机制与阻尼同时、独立存在11●线性系统中阻尼每周的耗散能为,一个抛物线●如果负阻尼力也是线性的,每周输入能量将是另一个抛物线●是自激系统还是阻尼系统,取决于哪个抛物线高一些12●在实际的例子中,输入和阻尼力其中之一或者同时,都是非线性的,输入和耗散曲线是相交的⏹假定振幅为,那么输入的能量就会多于耗散的能量,振幅会增加⏹假如振幅为,阻尼力会大于自激振动,振动会消减⏹这两种情况下,振幅都会倾向于向发展, 此时能量平衡,系统所做的运动为无阻尼的稳态自由振动1311.2稳定的数学判据●对于单自由度系统,采用简单的物理推理即可显示阻尼常数是否为负,因而可以不通过数学方法,而直接以物理方法推导动态稳定准则。



179第七章 弹性连续体振动的准确解实际的振系都是弹性连续体系统,在很多情况下只是为了使问题简化,计算简便,才把它们简化成前几章所讨论的有限多的离散系统来分析。
当需要对弹性体振动问题作严密的分析时,这时就需要作为连续系统来处理。
弹性连续体问题与离散体问题有不同的特点,弹性连续体的质量、刚度、阻尼是连续分布的,因之具有无限多个自由度,需用无限多个点的独立坐标来表确定,其运动微分方程需要用偏微分方程来描述,而离散体在力学模型上具有明显的集中质量和不计质量的弹性元件,其自由度有限,运动以与自由度个数相等的二阶常系数微分方程来描述。
尽管如此,但两类问题在物理本质上是相同的,若把连续系统的质量分段聚集到有限个点上,各点之间用弹性元件连接起来便成为连续体,反之,离散系统当其质点数趋于无限多时就成为连续体,它们之间有相同的动力特性。
n 自由度连续体系统有n 个固有频率及主振型,而连续体则有无限多个固有频率及主振型,连续体中也存在各个主振型之间关于质量矩阵、刚度矩阵的正交性,对弹性体的响应分析,主振型迭加法有效。
本章将研究具有以下三个条件的理想弹性连续体振动问题的求解:1.材料是均匀的,具有各向同性;2.应力不超过弹性极限、并服从虎克定律;3.变形是微小的且是连续的。
具体是一维弹性体:轴、杆、梁等。
至于其它类弹性连续体如板、壳等的振动问题,因涉及到弹性力学知识,本章将不予讨论。
7-1弦的横向振动先研究最简单的弦的横向振动问题。
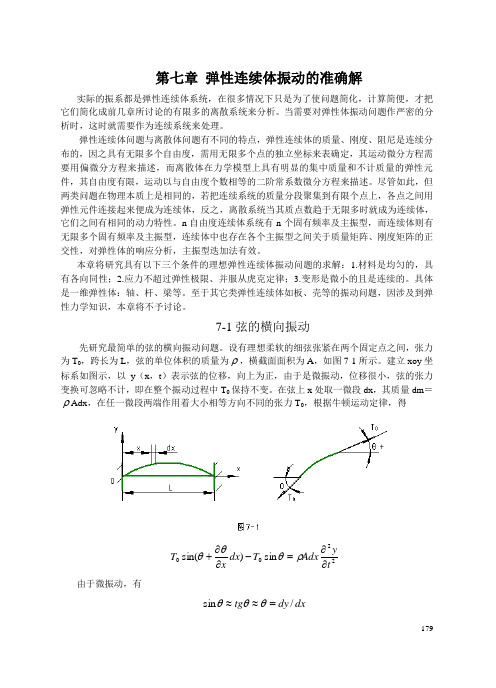
设有理想柔软的细弦张紧在两个固定点之间,张力为T 0,跨长为L ,弦的单位体积的质量为ρ,橫截面面积为A ,如图7-1所示。
建立xoy 坐标系如图示,以y (x ,t )表示弦的位移,向上为正,由于是微振动,位移很小,弦的张力变换可忽略不计,即在整个振动过程中T 0保持不变。
在弦上x 处取一微段dx ,其质量dm =ρAdx ,在任一微段两端作用着大小相等方向不同的张力T 0,根据牛顿运动定律,得2200sin )sin(tyAdx T dx x T ∂∂=-∂∂+ρθθθ由于微振动,有dx dy tg /sin =≈≈θθθ180故有2200)(ty Adx T dx x T ∂∂=-∂∂+ρθθθ代入x y∂∂=θ,简化后,即为 22220ty A x y T ∂∂=∂∂ρ 或写成22222t y a x y ∂∂=∂∂ (7-1) 式中AT a ρ0=称为波沿弦长度方向传播的速度。
弹性边界下附加大质量机器楼板振动分析随着城市建设快速推进,用电负荷不断增长,在紧缺的用地条件下,如何解决城市中心区域用地稀缺与用电需求之间的矛盾,是摆在政府部门和电力企业面前的重大课题。
在这样的实际背景下,附建式变电站以其不独立占地的显著优势应运而生。
然而,附建式变电站结构在放置于其楼板上的大质量机器正常运转过程中产生的简谐振动荷载的作用下会产生动力响应,可能会使处于其中的工作人员或者居民产生不舒适感,影响正常的工作生活。
这种大质量机器“上楼”影响楼中居民舒适性的现象,除了出现在附建式变电站结构的应用中,也出现在工业厂房、水电站等其他结构中。
论文针对这种大质量机器(如变压器)振动荷载对楼板上的振动及减振问题进行了深入的理论和数值分析和研究。
本论文研究工作主要包括了以下几个方面:首先,通过查阅大量国内外振动舒适度评价指标,对比各个舒适度指标,总结得到一个适用于附建式变电站振动舒适度评价的指标,即加速度评价指标。
其次,利用瑞利-里兹能量法,基于哈密顿变分原理,将矩形薄板体系的位移振型函数代入哈密顿变分方程,通过整理推导出以整体体系的自由振动固有频率为特征值,以位移振型函数中的傅里叶系数组成的向量为特征向量的标准特征方程。
通过对不同阶数的附加分布质量矩形薄板的振动控制微分方程进行变换积分,再根据格林公式的定义,推导得出判断附加分布质量的矩形薄板的模态振型正交性的数学公式。
在附加分布质量矩形薄板自由振动的基础上,将附加分布质量矩形薄板的横向位移函数分离变量为空间函数(即振型)和时间函数(广义坐标)的积,并利用振型的正交性推导出强迫振动作用下的振动位移响应的表达式。
在附加分布质量矩形薄板自由振动的基础上,在附加分布质量下添加隔振弹簧,对附加分布质量矩形薄板的隔振响应进行了讨论分析。
再次,用Mathematica和Matlab数学软件自行编程,求解典型边界条件下的模态和瞬态振动特性,并验证其振型的正交性。
并以四边简支边界条件下的附加变压器矩形薄板为例,分析了板的厚度、板长宽比、变压器的放置位置、弹性边界刚度四个参数对薄板体系的振动特性的影响。
收稿日期:1996-12-24*机械部教育司科研基金资助项目
加热弹性圆板的大振幅自由振动*李 世 荣(甘肃工业大学基础课部,兰州 730050)摘 要 基于vonKármán理论和Hamilton原理,导出了均匀加热弹性圆板用中面位移表示的大振幅自由振动动力学控制方程.并在调和振动模态假设下,采用Kan-
torovich平均方法将所得混合初-边值问题转化为相应的非线性常微分方程两点边值问题,采用打靶法和解析延拓法,分别获得了不可移简支和夹紧加热圆板非线性振动的调和振动响应,绘出了不同加热温度下的幅-频特征曲线.得出:升温使圆板的固有频率降低,从而实现改变板的温度对其固有频率的控制.关键词 加热圆板 大振幅振动 打靶法 解析延拓 固有频率分类号 O.343
受约束弹性构件在变温环境中的振动和热屈曲问题的研究对有效的工程设计具有十分重要的意义.关于薄板构件的热弯曲、热屈曲和热振动问题的研究状况可见Tauchert(1991)和Thornto(1993)的综述文章[1,2];文献[3]中采用Galerkin法研究了面内热应力作用下的圆薄板在热屈曲构形附近的微幅振动;在文献[4]中采用混合方法分析了变温产生的内力对矩形板和斜形板微幅振动的影响;Tani[5]采用有限差分格式研究了横向均布载荷作用下的加热环板在轴对称大变形弯曲平衡构形附近微幅振动的特征值问题;本文作者也曾采用摄动法与有限差分法有机结合的方法分别讨论过等厚度和变厚度环板在均匀变温场内的非线性振动问题[6,7].本文将以横向和径向位移作为基本未知量,讨论了周边受约束圆板在静态变温下的大振幅自由振动.
1 控制方程
考虑一半径为a,厚度为h的周边不可移圆形薄板,设板从自然状态起的均匀升温为T,分析该加热圆板的轴对称大振幅自由振动.忽略面内位移的惯性项,由Hamilton[8]原理可导出用中面位移表示的系统vonKármán型的无量纲动力学控制方程: 4w x4+2x 3w x3-1x2 2w x2+1x3 w x- 2w
f2+λx xx w
x
=12W2 xx u x+12 w x2+_xu w x(1) 2u x2+1x u x-ux2+ 2w x2 w x+1-_2x w x2=0(2)
第23卷第2期1997年6月甘 肃 工 业 大 学 学 报JournalofGansuUniversityofTechnologyVol.23No.2Jun.1997在x=0处,w有限, w x=0, u=0 (3)limx→0 3w x3+1x 2w x2=0(4)在x=1处,w=0, w x+k 2w x2=0, u=0(5)当f=0时,w=a(x), w f=0, u=Z(x)(6) 上述方程中各无量纲的含意分别为x=r/a, W=a/h, w=W/a,
u=U/a,f=t(D/d)12/T2, λ=12(1+_)W2TT(7)
式中 r径向坐标 f时间变量 W(r,t),U(r,t)中面的横向及径向位移 D抗弯刚度,D=Eh3[12(1-_2)]
E,_材料弹性模量及泊松比 d质量密度 T热膨胀系数 a(x),Z(x)无量纲初始位移 k=0,1/_分别表示圆板周边横向夹紧和简支边界条件设式(1~7)的动力响应为下列调和模式:w(x,f)=a(x)coskf, u(x,f)=Z(x)cos2kf(8)
其中,k为系统的无量纲固有频率.采用Kantorovich平均方法[7],可消去时间变量,将式(1~7)转化为a″″+2a /x-a″/x2+a′/x3+k2a+λ(a″+a′/x)=c[a′(Z″+a″a′+_Z′/x-_Z/x2)+(a″+a′/x)(Z′+a′2/2+_Z/x)](9)Z″+Z′/x-Z/x2+a′a″+(1-_)a′2/(2x)=0(10)
a(0)=A/W, a′(0)=0, Z(0)=0(11)limx→0(a +a″/x)=0(12)
a(1)=0, a′(1)+ka″(1)=0, Z(1)=0(13)其中,A=W(0,0)/h=a(0)W;c=9W2,式(9~13)中包含动力学参数k2,温度载荷参数λ和振幅参数(这里为非线性控制参数)A,构成一多参数的非线性常微分方程两点边值问题.其中若令k=0,c=12W2,则得圆板热过屈曲问题位移形式控制方程.
2 两点边值问题的打靶法式(9~13)为一组耦合的非线性常微分方程两点边值问题,其解析解难以求得.这里采用将边值问题初值化求解的打靶法来求其数值解.为此,先将式(9~13)记为下列标准形式:dYdx=H(x,Y,λ), Δx
·104·甘肃工业大学学报 第23卷B0Y(0)={A/W 0 0 0}T, B1Y(1)={0 0 0}T(15)式中 Y={y1 y2 y3 y4 y5 y6 y7}T={a a′ a″ a Z Z′ k2}T(16)H={y2 y3 y4 h y5 j 0}T(17)h=-2y4/x+y3/x2-y2/x3-y1y7-λ(y3+y2/x)
+c[y2(j+y2y3+_y6/x-_y5/x2)
+(y3+y2/x)(y6+y22/2+_y5/x)](18)
j=-y6/x+y5/x2-y2y3-(1-_)y22/(2x)(19)
B0=10000000100000001/Δx10000000100 B1=100000001k00000000100(20) 这里引入小量Δx>0,是为了避免横向无量纲剪力在x=0处的奇性.由a(x)在x=0处的连续性可知,当Δx充分小时中心无量纲振幅A可近似用a(Δx)W来代替.考察与式(14)和式(15)相应的初值问题:dYdx=H(x,Z;λ)(21)
Z(Δx)=I(A,D)(22)式中,Z,I,D为任意使初值问题有解的初始参数向量.Z={z1 z2 z3 z4 z5 z6 z7}T,I={A/W 0 d1 -d1/Δx 0 d2 d3}T, D={d1 d2 d3
}T.
设初值问题式(21,22)的解为
Z=Z(x;A,D,λ)=I(A,D)+∫xΔxH(x,Z,λ)dx(23) 于是,由常微分方程理论可知,对于确定的振幅参数A和变温参数λ,如果有D=D*=
{d*1 d*2 d*3}T,使Z(x;A,D*,λ)满足式(15)的第二个方程,即B1Z(1;A,D*,λ)={0 0 0}T(24)则可得边值问题式(14)和式(15)的解为Y(x;A,λ)=Z(x;A,D*,λ)(25) 从而可得混合问题(1~6)形如式(8)的解.上述分析过程称为常微分方程两点边值问题的打靶法(ShootingMethod)[9].
3 数值方法及结果由于方程(21,22)的解析解无法获得,因此,式(24)的具体形式是未知的.这里,采用变步长Runge-Kutta积分格式对方程(21,22)进行数值积分,用Newton-Raphson方法对方程组(24)进行迭代求解,并建立联立求解的数值计算过程,获得式(14,15)的数值解.具体编程和实现过程见文献[9],这里不再赘述.方程(14,15)连续性依赖于参数A的解Y(x;A,λ),可采用从其线性化问题(A→0)开始,使参数A小步递增的解析延拓法(AnalyticalContinuation)获得.具体计算时,取泊松比_=0.3,W=40,相对误差限EPS=10-5.取Δx=0.001近似地表
·105·第2期 李世荣:加热弹性圆板的大振幅自由振动示完善圆板.计算结果表明,这一近似引起的计算误差小于EPS.因此,可用A*近似表示圆板的中心无量纲振幅A.表1给出了A*=10-4,λ=0时周边不可移简支圆板的前几阶线性固有频率k0=d*3,并与Bessel函数[10]进行了比较,说明本文数值方法的可靠性和计算精度.由于表1 周边不可移简支圆板的前四阶线性固有频率k0
k(1)0k(2)0k(3)0k(4)0备 注
4.935229.72074.156138.32Bessel函数解[10]4.935229.72074.157138.32本文解
工程实际中主要关心振动系统的低阶频率,因此,下面着重分析圆板的基频.由式(25)可得下列特征关系:k=k(A,λ), λ≤λcr(26)其中,λcr是圆板热屈曲的无量纲临界温度.对应于支承参数分别为k=0,k=1/_的圆板,其临界温度分别是λcr=14.68,λcr=4.198.图1和图2分别给出上述两种支承圆板在不同无量纲变温λ下的k-A曲线.由此可见,升温可使板的固有频率降低,而降温会使固有频率增大.这是因为变温产生的面内应力会影响板的抗弯刚度.压应力使抗弯刚度减弱,而拉应力则使抗弯刚度增强.另外,从曲线的变化趋势来看,变温对线性固有频率的影响最大.随着振幅的增大,变温对非线性频率的影响逐渐减小.
图1 不同变温λ下的k-A曲线(k=0) 图2 不同变温λ下的k-A曲线(k=1/_)数值结果表明,一阶线性固有频率的平方k2与变温λ成线性关系:k2/k20+λ/λcr=1, λ≤λcr(27)
其中,k0为无变温时圆板的线性固有频率.当λ>λcr时,板已不具有形如式(8)的振动模态,问题将转化为圆板在热过屈曲构形附近的振动.这个问题将另文讨论.
4 结论1)面内变温产生的热应力对圆板的固有频率有影响.升温会使固有频率降低,降温会使固有频率升高.因此,可采用控制温度的办法来实现对系统频率的调节.2)本文所采用的数值分析方法具有普遍性,可直接用于任意非线性常微分方程两点边值问题的求解,所得结果是数值意义下的精确解,与摄动法及级数法相比具有明显的优点,它不
·106·甘肃工业大学学报 第23卷