全等三角形中常见辅助线的添加方法

全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变D C BAED F CB A换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”法构造全等三角形．3)遇到角平分线在三种添辅助线的方法4)（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

三角形全等添加辅助线口诀人说几何很困难点就在辅助线，辅助线，如何添加？把握定理和概念，还要刻苦加钻研，找出规律凭经验，图中有角平分线，可向两边引垂线，也可将图对折看，对称以后关系现，角平分线平行线，等腰三角形来添，角平分线加垂线，三线合一试试看，线段垂直平分线，常向两边把线连，要证线段倍与半，延长缩短可试验，三角形中两中点，连接则成中位线，三角形中有中线，延长中线等中线。

几何，不谈战术谈战略学而思中考研究中心施佳辰作为和代数并列为初中数学两大知识点的几何，常常因为图形变化多端，方法多种多样而被称为数学中的变形金刚。

话虽如此，变形金刚也不是无敌的，最终仍旧是人类的智慧更胜一筹。

实际上，每一道几何题目背后都有着一定的法则和规律，每一类题都有着相似的解题思想，这种思想的集中体现，便是模型（变形金刚的原力所在）对于几何，我们不仅仅要在战术上坚定执行，在战略层面上也要对几何在初中三年的整体学习有一个明确的了解。

得模型者得几何，而模型思想的建立又并非一朝一夕，是需要同学们在大量的实战做题和不断总结方法中培养出来的。

对于模型的理解和认识，分为很多层面，最浅的是基本的形似，看到图形相仿或相似的题目，能够有意识的联想以前学过的题型并加以运用，套用，这是最简单的模型思想。

高一些的是神似，看到一些关键点，关键线段或是题目所给条件的相似便能够联想到所学知识点，通过推理和演绎逐步取得正确的解法，记住的是一些具体模型，这，是第二种层次。

最高的境界是，心中只有很少几种基本模型，这些模型就像种子，看到一道题目就会发芽，开花结果，随着对于题目的深入理解，不断地寻找适合的花朵，每一朵花上面都有着一种具体的模型，而每种模型之间，都会有树枝相连，相互间并不是孤立的，而是借由其他条件贯穿连接的。

达到这样的理解才能算是包罗万象，驾轻就熟。

我们对于模型的把控能不应当仅限于会用于具有明显模型特征的题目，对于一些特征并不明显的题目，我们要有能力添加辅助线去挖掘图形当中的隐藏属性。

全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”法构造全等三角形．D C BAED F CB A3)遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

做三角形辅助线图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

线段和差及倍半，延长缩短可试验。

线段和差不等式，移到同一三角去。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.由角平分线想到的辅助线：图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等。

对于有角平分线的辅助线的作法，一般有两种。

①从角平分线上一点向两边作垂线；②利用角平分线，构造对称图形（如作法是在一侧的长边上截取短边）。

通常情况下，出现了直角或是垂直等条件时，一般考虑作垂线；其它情况下考虑构造对称图形。

至于选取哪种方法，要结合题目图形和已知条件。

与角有关的辅助线 （一）、截取构全等如图1-1，∠AOC=∠BOC ，如取OE=OF ，并连接DE 、DF ，则有△OED ≌△OFD ，从而为我们证明线段、角相等创造了条件。

例1． 如图1-2，AB//CD ，BE 平分∠BCD ，CE 平分∠BCD ，点E 在AD 上，求证：BC=AB+CD 。

（二）、角分线上点向角两边作垂线构全等过角平分线上一点向角两边作垂线，利用角平分线上的点到两边距离相等的性质来证明问题。

如图2-1，已知AB>AD, ∠BAC=∠FAC,C D=BC 。

求证：∠ADC+∠B=180图1-1O ABD EFC图1-2ADBCEF图2-1ABCDEF（三）：作角平分线的垂线构造等腰三角形从角的一边上的一点作角平分线的垂线，使之与角的两边相交，则截得一个等腰三角形，垂足为底边上的中点，该角平分线又成为底边上的中线和高，以利用中位线的性质与等腰三角形的三线合一的性质。

（如果题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交）。

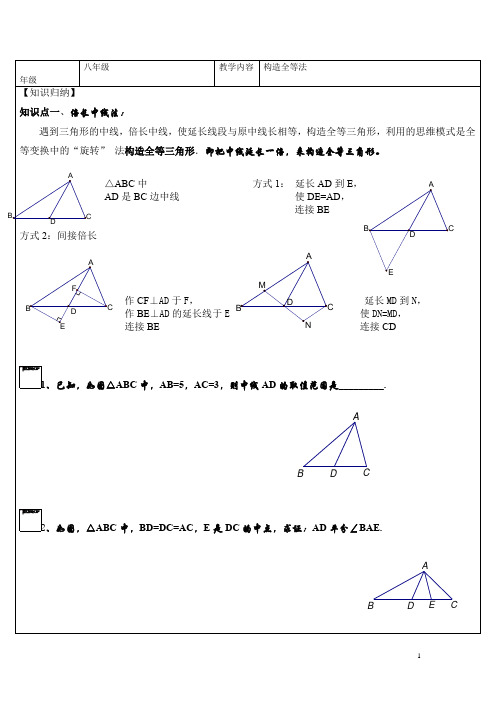
D C B A 年级【知识归纳】知识点一、倍长中线法：遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．即把中线延长一倍，来构造全等三角形。

△ABC 中 方式1： 延长AD 到E ，AD 是BC 边中线 使DE=AD ，连接BE方式2：间接倍长作CF ⊥AD 于F ， 延长MD 到N ， 作BE ⊥AD 的延长线于E 使DN=MD ，连接BE 连接CD1、已知，如图△ABC 中，AB=5，AC=3，则中线AD 的取值范围是_________.2、如图，△ABC 中，BD=DC=AC ，E 是DC 的中点，求证：AD 平分∠BAE.E D CB AD A CE D A B CF E D C B A N DC BAMO EDCBA3、已知，如图1-1，在四边形ABCD 中，BC ＞AB ，AD =DC ，BD 平分∠ABC .求证：∠BAD +∠BCD =180°.巩固练习：如图2-2，在△ABC 中，∠A=90 ，AB=AC ，∠ABD=∠CBD 。

求证：BC=AB+AD1：如图，已知在△ABC 中，∠B=60°，△ABC 的角平分线AD,CE 相交于点O ，求证：OE=ODABCD图1-1图2-2ABCDE（二）：作角平分线的垂线构等腰三角形从角的一边上的一点作角平分线的垂线，使之与角的两边相交，则截得一个等腰三角形，垂足为底边上的中点，该角平分线又成为底边上的中线和高，以利用中位线的性质与等腰三角形的三线合一的性质。

（如果题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交）。

4、如图3-2，AB=AC ，∠BAC=90 ，AD 为∠ABC 的平分线，CE ⊥BE.求证：BD=2CE 。

（三）、以角分线上一点做角的另一边的平行线有角平分线时，常过角平分线上的一点作角的一边的平行线，从而构造等腰三角形。

全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．3)遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂D C BAED F CB A线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

全等三角形中辅助线的添法(三大模型)【模型一：倍长中线模型】1.(23-24八年级上·江苏·期末)如图，在△ABC 中．AD 是BC 边上的中线，交BC 于点D．(1)如下图，延长AD 到点E ，使DE =AD ，连接BE ．求证：△ACD ≌△EBD．(2)如下图，若∠BAC =90°，试探究AD 与BC 有何数量关系，并说明理由．(3)如下图，若CE 是边AB 上的中线，且CE 交AD 于点O ．请你猜想线段AO 与OD 之间的数量关系，并说明理由．【思路点拨】(1)利用SAS 可得△ACD ≌△EBD ；(2)延长AD 到点E ，使DE =AD ，连接BE ，先根据△ACD ≌△EBD 证得∠C =∠CBE ，AC =BE ，进而得到AC ∥EB ，AD =12AE ；再证得△ABC ≌△BAE SAS 利用全等三角形全等的性质即可；(3)延长OE 到点M ，使EM =OE ，连接AM ．延长OD 到点N ，使DN =OD ，连接BM ，BN ，BO ，证得△MOB ≌△NBO ASA 可得MB =NO ，进而得到AO =2OD ，本题考查了全等三角形的判定与性质，三角形的中线，熟练掌握全等三角形的判定方法是解题的关键．【解题过程】(1)证明：在△ACD 和△EBD 中，DA =DE∠ADC =∠EDBDC =DB∴△ACD ≌△EBD SAS ；(2)解：AD =12BC ，理由如下：延长AD 到点E ，使DE =AD ，连接BE ，如图由(1)得△ACD ≌△EBD ，∴∠C =∠CBE ，AC =BE∴AC ∥EB ，AD =12AE ∴∠BAC +∠ABE =180°，∵∠BAC =90°，∴∠ABE =90°，∴∠BAC =∠ABE在△ABC 和△BAE 中AC =BE∠BAC =∠ABEAB =AB∴△ABC ≌△BAE SAS ∴BC =AE ，∴AD =12BC ；(3)AO =2OD ，理由如下：延长OE 到点M ，使EM =OE ，连接AM ．延长OD 到点N ，使DN =OD ，连接BM ，BN ，BO ，如图，由(1)得△AOE ≌△BME ，△ODC ≌△NDB ，∴∠AOE =∠BME ，∠OCD =∠NBD ，AO =BM ，∴AO ∥BM ，OC ∥NB ，∴∠MBO =∠BON ，∠MOB =∠NBO在△MOB 和△NBO 中，∠MBO =∠BONOB =OB ∠MOB =∠NBO，∴△MOB ≌△NBO ASA ∴MB =NO ，∴AO =2OD ．2.(23-24八年级上·广西北海·期末)八年级数学课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC 中，若AB =9，AC =5，求BC 边上的中线AD 的取值范围．小红在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE =AD ，请根据小红的方法思考作答：(1)由已知和作图能得到△ADC ≌△EDB 的理由是；A.SSS B.SAS C.AASD.HL(2)求得AD的取值范围是；A.5<AD<9B.5≤AD≤9C.2<AD<7D.2≤AD≤7(3)归纳总结：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．完成上题之后，小红善于探究，她又提出了如下的问题，请你解答．如图2，在△ABC中，点E在BC上，且DE=DC，过E作EF∥AB，且EF=AC．求证：AD平分∠BAC．【思路点拨】本题是三角形综合题，考查了倍长中线法解题，全等三角形的判定和性质，等腰三角形的判定和性质，熟练掌握倍长中线法，灵活进行三角形全等的证明，是解题的关键．(1)根据三角形全等的判定定理去选择即可；(2)根据三角形全等的性质和三角形三边关系定理计算即可；(3)由“SAS”可证△EFD≌△CMD，可得EF=DM，∠EFD=∠M，由平行线的性质和等腰三角形的性质可证∠M=∠BAD=∠CAM，可得AD平分∠BAC．【解题过程】(1)解：延长AD到点E，使DE=AD，∵BD=CD，在△ADC和△EDB中，CD=BD∠ADC=∠BDEAD=DE，∴△ADC≌△EDB(SAS)，故选：B．(2)解：∵△ADC≌△EDB，∴AC=EB，∵AB=9，AC=5，AB-BE<AE<AB+BE，∴4<2AD<14，∴2<AD<7，故选：C；(3)证明：如图，延长AD至M，使DM=DF，连接CM，∵DE=DC，∠EDF=∠CDM，DF=DM，∴△EFD≌△CMD(SAS)，∴EF=DM，∠EFD=∠M，∴EF∥CM，∵EF∥AB，∴CM∥AB，∴∠BAD=∠M，∵EF=AC，∴EF=DM=AC，∴∠CAM=∠M，∴∠BAD=∠CAM，∴AD平分∠BAC．3.(23-24八年级上·安徽安庆·期末)(1)如图①，在△ABC中，若AB=6，AC=4，AD为BC边上的中线，求AD的取值范围；(2)如图②，在△ABC中，点D是BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，判断BE+CF与EF的大小关系并证明；(3)如图③，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．【思路点拨】(1)由已知得出AB-BE<AE<AB+BE，即6-4<AE<6+4，AD为AE的一半，即可得出答案；(2)延长FD至点M，使DM=DF，连接BM，EM，可得△BMD≌△CFD，得出BM=CF，由线段垂直平分线的性质得出EM=EF，在△BME中，由三角形的三边关系得出BE+BM>EM即可得出结论；(3)延长AE，DF交于点G，根据平行和角平分线可证AF=FG，也可证得△ABE≌△GCE，从而可得AB= CG，即可得到结论．【解题过程】解：(1)如图①，延长AD到点E，使DE=AD，连接BE，∵D是BC的中点，∴BD=CD，∵∠ADC=∠BDE，∴△ACD≌△EBD SAS，∴BE=AC=4，在△ABE中，AB-BE<AE<AB+BE，∴6-4<AE<6+4，，∴2<AE<10，∴1<AD<5，故答案为：1<AD<5；(2)BE+CF>EF，理由如下：延长FD至点M，使DM=DF，连接BM、EM，如图②所示．同(1)得：△BMD≌△CFD SAS，∴BM=CF，∵DE⊥DF，DM=DF，∴EM=EF，在△BME中，由三角形的三边关系得：BE+BM>EM，∴BE+CF>EF；(3)AF +CF =AB ，理由如下：如图③，延长AE ，DF 交于点G ，∵AB ∥CD ，∴∠BAG =∠G ，在△ABE 和△GCE 中，CE =BE ，∠BAG =∠G ，∠AEB =∠GEC，∴△ABE ≌△GEC AAS ，∴CG =AB ，∵AE 是∠BAF 的平分线，∴∠BAG =∠GAF ，∴∠FAG =∠G ，∴AF =GF ，∵FG +CF =CG ，∴AF +CF =AB ．4.(23-24八年级上·江苏南通·期中)课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC 中，若AB =6,AC =4，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图1所示，延长AD 到点E ，使DE =AD ，连接BE．请根据小明的思路继续思考：(1)由已知和作图能证得△ADC ≌△EDB ，得到BE =AC ，在△ABE 中求得2AD 的取值范围，从而求得AD 的取值范围是．方法总结：上述方法我们称为“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系；(2)如图2，AD 是△ABC 的中线，AB =AE ,AC =AF ,∠BAE +∠CAF =180°，试判断线段AD 与EF 的数量关系，并加以证明；(3)如图3，在△ABC 中，D ,E 是BC 的三等分点．求证：AB +AC >AD +AE ．【思路点拨】本题考查了三角形三边关系，三角形全等的性质与判定，利用倍长中线辅助线方法是解题的关键．(1)延长AD 到点E ，使DE =AD ，连接BE ，根据题意证明△MDB ≌△ADC ，可知BM =AC ，在△ABM 中，根据AB -BM <AM <AB +BM ，即可；(2)延长AD 到M ，使得DM =AD ，连接BM ，由(1)的结论以及已知条件证明△ABM ≌△EAF ，进而可得AM =2AD ，由AM =EF ，即可求得AD 与EF 的数量关系；(3)，取DE 中点H ，连接AH 并延长至Q 点，使得AH =QH ，连接QE 和QC ，通过“倍长中线”思想全等证明，进而得到AB =CQ ，AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论．【解题过程】(1)解：如图1所示，延长AD到点E，使DE=AD，连接BE．∵AD是△ABC的中线，∴BD=CD，在△MDB和△ADC中，BD=CD∠BDM=∠CDA DM=AD，∴△MDB≌△ADC(SAS)，∴BM=AC=4，在△ABM中，AB-BM<AM<AB+BM，∴6-4<AM<6+4，即2<AM<10，∴1<AD<5，故答案为：1<AD<5．(2)EF=2AD，理由：如图2，延长AD到M，使得DM=AD，连接BM，由(1)知，△BDM≌△CDA(SAS)，∴BM=AC，∠M=∠MAC∵AC=AF，∴BM=AF，∵∠MBA+∠M+∠BAM=180°，即∠MBA+∠BAC=180°，又∵∠BAE+∠CAF=180°，∴∠EAF+∠BAC=180°，∴∠EAF=∠MBA，又∵AB=EA，∴△ABM≌△EAF(SAS)，∴AM=EF，∵AD=DM，∴AM=2AD，∵AM=EF，∴EF=2AD．(3)证明：如图所示，取DE中点H，连接AH并延长至Q点，使得AH=QH，连接QE和QC，∵H为DE中点，D、E为BC三等分点，∴DH=EH,BD=DE=CE，∴DH=CH，在△ABH和△QCH中，BH=CH∠BHA=∠CHQ AH=OH，∴△ABH≌△QCH(SAS),同理可得:△ADH≌△QEH,∴AB=CQ,AD=EQ，此时,延长AE交CQ于K点，∵AC+CQ=AC+CK+QK,AC+CK>AK，∴AC+CQ>AK+QK，∵AK+QK=AE+EK+QK>QE,EK+QK>QE，∴AK+QK>AE+QE，∴AC +CQ >AK +QK >AE +QE ，∵AB =CQ ,AD =EQ ，∴AB +AC >AD +AE ．5.(23-24七年级下·广东佛山·期中)【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图，△ABC 中，AB =8，AC =6，求BC 边上的中线AD 的取值范围，经过组内合作交流．小明得到了如下的解决方法：延长AD 到点E ，使DE =AD请根据小明的方法思考：(1)求得AD 的取值范围是；【问题解决】请利用上述方法(倍长中线)解决下列三个问题如图，已知∠BAC +∠CDE =180°，AB =AC ，DC =DE ，P 为BE 的中点．(2)如图1，若A ，C ，D 共线，求证：AP 平分∠BAC ；(3)如图2，若A ，C ，D 不共线，求证：AP ⊥DP ；(4)如图3，若点C 在BE 上，记锐角∠BAC =x ，且AB =AC =CD =DE ，则∠PDC 的度数是(用含x 的代数式表示)．【思路点拨】(1)根据三角形三边之间的关系：两边之和大于第三边，两边之差小于第三边，即可进行解答；(2)延长DP 交AB 延长线于点F ，证△APF ≌△APD 即可；(3)延长DP 至点F ，使得PF =PD ，连接BF 、AF 、AD ，证△APF ≌△APD 即可；(4)过点C 作CM ⊥BC 交AP 于点M ，由(3)可得∠APD =90°，证△ACM ≌△DCP ，用含x 的代数式表示出∠PDC 即可．【解题过程】(1)∵AD 为BC 边上的中线，∴BD =CD ，在△ADC 和△EDB 中，BD =CD∠ADC =∠EDBAD =ED∴△ADC ≌△EDB SAS ，∴BE =AC =6，∵AB =8，∴8-6<AE <8+6，即2<AE <14，∵DE =AD ，∴AD =12AE ，∴1<AD <7，故答案为：1<AD <7(2)如下图，DP 交AB 延长线于点F∠BAC +∠CDE =180°，∴AF ∥DE (同旁内角互补，两直线平行)，∴∠PFB =∠PDE ，∠PBF =∠PED ，∵P 为BE 的中点∴BP =PE ，∴△BPF ≌△EPD AAS ，∴BF =DE =DC ，PD =PF ，又∵AB =AC ，∴AB +BF =AC +DC ，即AF =AD ，在△APF 和△APD 中PF =PDAP =APAF =AD∴△APF ≌△APD (SSS )，∴∠P AF =∠P AD (全等三角形的对应角相等)，即AP 平分∠BAC(3)延长DP 至点F ，使得PF =PD ，连接BF 、AF 、AD由(1)同理易知△DPE ≌△FBP (SAS )，∴BF =DE =CD ，∠E =∠FBP ，∵∠BAC +∠CDE =180°，且∠BAC +∠CAD +∠ADC +∠CDE +∠E =360°，∠CAD +∠C +∠ADC =180°，∴∠ABF =∠ACD ，AB =AC ，∴△ABF ≌△ACD (SAS )，∴AF =AD ，∴△APF ≌△APD (SSS )，∴∠APD =∠APF =180°÷2=90°，∴AP ⊥DP(4)过点C 作CM ⊥BC 交AP 于点M ，由(3)可得∠APD =90°，∠BAC =x ，∠BAC+∠CDE =180°，AB =AC =CD =DE ，∴∠ACB =180°-x 2=90°-x 2，∴∠DCE =90°-∠CDE 2=90°-180°-x 2=x 2，∴∠ACB和∠DCE 互余，∠ACD =∠MCP =∠APD =90°，∴∠ACM =∠DCP =x 2，∠CAM =∠CDP ∴△ACM ≌△DCP (ASA )，∴MC =PC ，∴∠BP A =45°，又∵∠ACB =90°-x 2，∴∠PDC =∠P AC =∠ACB -∠APB =45°-x 2，故答案为：45°-x 2【模型二：旋转模型(截长补短)】6.(23-24八年级上·湖北武汉·期末)如图，在五边形ABCDE 中，∠B =∠E =90°，∠CAD =12∠BAE ，AB =AE ，且CD =3，AE =4，则五边形ABCDE 的面积为()A.6 B.8 C.10 D.12【思路点拨】本题考查了旋转的性质、全等三角形的判定与性质、三点共线，解题的关键是利用全等的性质将面积进行转化．将△ABC 绕点A 逆时针旋转至△AEF ，首先证明点D ，E ，F 三点共线，证明△ACD ≌△AFD (SAS )，得到CD =DF =3，S △ACD =S △AFD ，再将所求面积转化为2S △AFD 进行计算即可．【解题过程】解：如图，将△ABC 绕点A 逆时针旋转至△AEF ，∵AB =AE ，∠B =∠E =90°，则AF =AC ，∠B =∠AED =∠AEF =90°，∴∠DEF =180°，即点D ，E ，F 三点共线，∵∠CAD =12∠BAE ，∠BAC +∠DAE =∠DAE +∠EAF =∠CAD ，即∠FAD =∠CAD ，在△ACD 和△AFD 中，AC =AF∠CAD =∠FAD AD =AD，∴△ACD ≌△AFD (SAS )∴CD =DF ，S △ACD =S △AFD∵CD =3，∴DF =3，五边形ABCDE 的面积为：S 四边形ACDE +S △ABC =S 四边形ACDE +S △AEF=S △ACD +S △AFD =2S △AFD ，=2×12×DF ×AE ，=2×12×3×4=12．故选：D ．7.(23-24八年级上·上海·期中)如图所示，已知AC 平分∠BAD ，∠B +∠D =180°，CE ⊥AB 于点E ，判断AB 、AD 与BE 之间有怎样的等量关系，并证明．【思路点拨】在AB 上截取EF ，使EF =BE ，联结CF ．证明△BCE ≌△ECF (SAS )，得到∠B =∠BFC ，又证明△AFC ≌△ADC ，得到AF =AD ，最后结论可证了．【解题过程】证明：在AB 上截取EF ，使EF =BE ，联结CF ．∵CE ⊥AB∴∠BEC =∠FEC =90°在△BCE 和△ECF{BE =EF∠BEC =∠FECCE =CE∴△BCE ≌△ECF (SAS )∴∠B =∠BFC∵∠B +∠D =180°又∵∠BFC +∠AFC =180°∴∠D =∠AFC∵AC 平分∠BAD∴∠FAC =∠DAC在△AFC 和△ADC 中{∠AFC =∠D∠FAC =∠DACAC =AC∴△AFC≌△ADC(AAS)∴AF=AD∵AB=AF+BE+EF∴AB=AD+2BE8.(23-24八年级上·山东临沂·期中)【基本模型】(1)如图1，ABCD是正方形，∠EAF=45°，当E在BC边上，F在CD边上时，请你探究BE、DF与EF之间的数量关系，并证明你的结论．【模型运用】(2)如图2，ABCD是正方形，∠EAF=45°，当E在BC的延长线上，F在CD的延长线上时，请你探究BE、DF与EF之间的数量关系，并证明你的结论．【思路点拨】本题主要考查全等三角形的判定和性质．本题蕴含半角模型，遇到半角经常要通过旋转构造全等三角形．(1)结论：EF=BE+DF．将△ADF绕点A顺时针旋转，使AD与AB重合，得到△ABF ，然后求出∠EAF =∠EAF=45°，利用“边角边”证明△AEF和△AEF 全等，根据全等三角形对应边相等可得EF=EF ，从而得解；(2)结论：EF=BE-DF，证明方法同法(1)．【解题过程】解：(1)结论：EF=BE+DF．理由：如图1，将△ADF绕点A顺时针旋转，使AD与AB重合，得到△ABF ，则：∠F AB=∠DAF,∠ABF =∠D=90°，AF=AF ，BF =DF，∴∠ABF +∠ABC=180°，即：F ,B,E三点共线，∵∠EAF=45°，∴∠DAF+∠BAE=90°-∠EAF=45°，∴∠BAF +∠BAE=45°，∴∠EAF =∠EAF=45°，在△AEF 和△AEF 中，AF =AF∠EAF =∠EAF AE =AE，∴△AEF ≌△EAF (SAS )，∴EF =EF ，又EF =BE +BF ，∴EF =BE +DF ．(2)结论：EF =BE -DF ．理由：如图2，将△ADF 绕点A 顺时针旋转，使AD 与AB 重合，得到△ABF ，则：BF =DF ,AF =AF ，同法(1)可得：△AEF ≌△AEF (SAS )，∴EF =EF ，又EF =BE -BF =BE -DF ，∴EF =BE -DF ．9.(23-24八年级上·湖北武汉·周测)(1)如图，在四边形ABCD 中，AB =AD，∠B +∠D =180°，E 、F 分别是边BC 、CD 上的点，且∠EAF =12∠BAD ．求证：EF =BE +FD ；(2)如图，在四边形ABCD 中，AB =AD ，∠B +∠ADC =180°，E 、F 分别是边BC 、CD 延长线上的点，且∠EAF =12∠BAD ．(1)中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【思路点拨】(1)延长CB 至M ，使BM =DF ，连接AM ．先证明△ABM ≌△ADF ，得到AF =AM ，∠2=∠3，再证明△AME ≌△AFE ，得到EF =ME ，进行线段代换，问题得证；(2)在BE 上截取BG ，使BG =DF ，连接AG ．先证明△ABG ≌△ADF ，得到AG =AF ，再证明△AEG ≌△AEF ，得到EG =EF ，进行线段代换即可证明EF =BE -FD ．【解题过程】解：(1)证明：如图，延长CB 至M ，使BM =DF ，连接AM ．∵∠ABC +∠D =180°，∠1+∠ABC =180°，∴∠1=∠D ，在△ABM 与△ADF 中，AB =AD∠1=∠D BM =DF，∴△ABM ≌△ADF (SAS )．∴AF =AM ，∠2=∠3．∵∠EAF =12∠BAD ，∴∠2+∠4=12∠BAD =∠EAF ．∴∠3+∠4=∠EAF ，即∠MAE =∠EAF ．在△AME 与△AFE 中，AM =AF∠MAE =∠EAF AE =AE，∴△AME ≌△AFE (SAS )．∴EF =ME ，即EF =BE +BM ，∴EF =BE +DF ；(2)结论EF =BE +FD 不成立，应当是EF =BE -FD ．证明：如图，在BE 上截取BG ，使BG =DF ，连接AG ．∵∠B +∠ADC =180°，∠ADF +∠ADC =180°，∴∠B =∠ADF ．∵在△ABG 与△ADF 中，AB =AD∠ABG =∠ADF BG =DF，∴△ABG ≌△ADF (SAS )，∴∠BAG =∠DAF ，AG =AF ，∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD ，∴∠GAE =∠EAF ．在△AGE 与△AFE 中，AG =AF∠GAE =∠EAF AE =AE，∴△AEG ≌△AEF ，∴EG =EF ，∵EG =BE -BG ，∴EF =BE -FD ．10.(23-24八年级上·贵州黔东南·期末)【初步探索】(1)如图1，在四边形ABCD 中，AB =AD ，∠B =∠ADC =90°，∠BAD =120°，E 、F 分别是BC 、CD 上的点，且∠EAF =60°，探究图中BE 、EF、FD 之间的数量关系．小芮同学探究此问题的方法是：延长FD 到点G ，使DG =BE ，连接AG ，先证明：△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论应是；【灵活运用】(2)如图2，若在四边形ABCD中，AB=AD，∠B+∠D=∠180°，∠BAD=120°，E、F分别是BC、CD上的点，且∠EAF=60°，(1)中的结论是否仍然成立，说明理由．【拓展延伸】(3)如图3，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，满足EF=BE+FD，请判断∠EAF与∠DAB的数量关系．并证明你的结论．【思路点拨】本题属于四边形综合题，主要考查了全等三角形的判定以及全等三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应角相等进行推导变形．解题时注意：同角的补角相等．(1)根据SAS可判定△ABE≌△ADG，进而得出∠BAE=∠DAG，AE=AG，再根据SAS判定△AEF≌△AGF，可得出EF=GF=DG+DF=BE+DF，据此得出结论；(2)延长FD到点G，使DG=BE，连接AG，先根据SAS判定△ABE≌△ADG，进而得出∠BAE=∠DAG，AE=AG，再根据SAS判定△AEF≌△AGF，可得出EF=GF=DG+DF=BE+DF；(3)在DC延长线上取一点G，使得DG=BE，连接AG，先根据SAS判定△ADG≌△ABE，再根据SAS判定△AEF≌△AGF，得出∠FAE=∠FAG，最后根据∠FAE+∠FAG+∠GAE=360°，推导得到2∠FAE+∠DAB=360°，即可得出结论．【解题过程】解：(1)BE+FD=EF．理由如下：如图1，延长FD到点G，使DG=BE，连接AG，∵∠ADC=90°，∴∠ADG=180°-∠ADC=90°，又∵∠B=90°，∴∠B=∠ADG，在△ABE与△ADG中，AB=AD∠B=∠ADG BE=DG，∴△ABE≌△ADG(SAS)，∴∠BAE=∠DAG，AE=AG，∵∠BAD=120°，∠EAF=60°，∴∠BAE+∠DAF=∠BAD-∠EAF=60°，∴∠DAG+∠DAF=60°，即∠GAF=60°，∴∠GAF=∠EAF；在△AEF与△AGF中，AE=AG∠EAF=∠GAF AF=AF，∴△AEF≌△AGF(SAS)，∴EF=GF，∵GF=DG+DF，∴EF=BE+DF，故答案为：BE+FD=EF；(2)(1)中的结论仍成立，理由如下：如图2，延长FD到点G，使DG=BE，连接AG，∠B+∠ADF=180°，∠ADG+∠ADF=180°，∴∠B=∠ADG，又∵AB=AD，∴△ABE≌△ADG(SAS)，∴∠BAE=∠DAG，AE=AG，∵∠BAD=120°120°，∠EAF=60°，∴∠BAE+∠DAF=60°，∴∠DAG+∠DAF=60°，∴∠GAF=∠EAF=60°，又∵AF=AF，∴△AEF≌△AGF(SAS)，∴EF=FG=DG+DF=BE+DF；(3)∠EAF=180°-12∠DAB．证明：如图3，延长DC到点G，使DG=BE，连接AG，∵∠ABC+∠ADC=180°，∠ABC+∠ABE=180°，∴∠ADC=∠ABE，在△ABE与△ADG中，AB=AD∠B=∠ADG BE=DG，∴△ADG≌△ABE(SAS)，∴AG=AE，∠DAG=∠BAE，∵EF=BE+FD，∴EF=DG+FD，∴EF=GF，在△AEF与△AGF中，AE=AG EF=GF AF=AF，∴△AEF≌△AGF(SSS)，∴∠FAE=∠FAG，∵∠FAE+∠FAG+∠GAE=360°，∴2∠FAE+(∠GAB+∠BAE)=360°，∴2∠FAE+(∠GAB+∠DAG)=360°，即2∠FAE+∠DAB=360°，∴∠EAF=180°-12∠DAB．【模型三：“K子”型(一线三垂直)】11.(23-24八年级上·广东江门·阶段练习)已知，△ABC中，∠BAC=90°，AB=AC，直线m过点A，且BD⊥m于D，CE⊥m于E，当直线m绕点A旋转至图1位置时，我们可以发现DE=BD+CE．(1)当直线m绕点A旋转至图2位置时，问：BD与DE、CE的关系如何？请予证明；(2)直线m在绕点A旋转一周的过程中，BD、DE、CE存在哪几种不同的数量关系？(直接写出，不必证明)【思路点拨】(1)利用条件证明△ABD≌△CAE，再结合线段的和差可得出结论；(2)根据图，可得BD、DE、CE存在3种不同的数量关系；【解题过程】(1)证明：如图2，∵BD⊥m，CE⊥m，∴∠BDA=∠CEA=90°，∴∠ABD+∠DAB=90°．∵∠BAC=90°，∴∠DAB+∠CAE=90°，∴∠ABD=∠CAE．在△ABD和△CAE中，∠BDA=∠CBA ∠ABD=∠CAB AB=CA，∴△ABD≌△CAE(AAS)，∴AD=CE，BD=AE∵DE=AE-AD，(2)直线m 在绕点A 旋转一周的过程中，BD 、DE 、CE 存在3种不同的数量关系：DE =BD +CE ，DE =BD -CE ，DE =CE -BD．如图1时，DE =BD +CE ，如图2时，DE =BD -CE ，如图3时，DE =CE -BD ，(证明同理)12.(23-24八年级上·贵州铜仁·阶段练习)(1)如图1，已知△ABC 中，∠BAC =90°，AB =AC ，直线m 经过点A ,BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D ,E ．求证：DE =BD +CE ．(2)如图2，将(1)中的条件改为：在△ABC 中，AB =AC ,D ,A ,E 三点都在直线m 上，并且有∠BDA =∠AEC =∠BAC ．请写出DE ,BD ,CE 三条线段的数量关系，并说明理由．【思路点拨】(1)利用已知得出∠CAE =∠ABD ，进而利用AAS 得出则△ABD ≌△CAE ，即可得出DE =BD +CE ；(2)根据∠BDA =∠AEC =∠BAC ，得出∠CAE =∠ABD ，在△ADB 和△CEA 中，根据AAS 证出△ADB ≌△CEA ，从而得出AE =BD ，AD =CE ，即可证出DE =BD +CE ；【解题过程】(1)DE =BD +CE ．理由如下：∵BD ⊥m ，CE ⊥m ，∴∠BDA =∠AEC =90°又∵∠BAC =90°，∴∠BAD +∠CAE =90°，∠BAD +∠ABD =90°，∴∠CAE =∠ABD在△ABD 和△CAE 中，∠ABD =∠CAE∠ADB =∠CEA =90°AB =AC，∴△ABD ≌△CAE (AAS )∴BD =AE ，AD =CE ，∵DE =AD +AE ，(2)DE =BD +CE ，理由如下：∵∠BDA =∠AEC =∠BAC ，∴∠DBA +∠BAD =∠BAD +∠CAE ，∴∠CAE =∠ABD ，在△ADB 和△CEA 中，∠ABD =∠CAE∠ADB =∠CEA AB =AC，∴△ADB ≌△CEA (AAS )，∴AE =BD ，AD =CE ，∴BD +CE =AE +AD =DE ．13.(23-24八年级上·山西大同·阶段练习)某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．(1)如图1．已知：在△ABC 中，∠BAC =90°，AB =AC ，直线l 经过点A ，BD ⊥直线l ，CE ⊥直线l ，垂足分别为点D 、E ．证明：DE =BD +CE ．(2)组员小明对图2进行了探究，若∠BAC =90°，AB =AC ，直线l 经过点A ．BD ⊥直线l ，CE ⊥直线l ，垂足分别为点D 、E ．他发现线段DE 、BD 、CE 之间也存在着一定的数量关系，请你直接写出段DE 、BD 、CE 之间的数量关系，(3)数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG (正方形的4条边都相等，4个角都是直角)，AH 是BC 边上的高，延长HA 交EG 于点I ，若BH =3，CH =7，求AI 的长．【思路点拨】(1)根据BD ⊥直线l ，CE ⊥直线l ，∠BAC =90°，可得∠CAE =∠ABD ，利用AAS 可证明△ADB ≌△CEA ，根据DE =AE +AD 即可得到DE =BD +CE ；(2)同(1)利用AAS 可证明△ADB ≌△CEA ，根据DE =AE -AD 即可得到DE =BD -CE ；(3)过E 作EM ⊥HI 于M ，GN ⊥HI 的延长线于N ，可构造两组一线三直角全等模型，即：△ABH ≌△EAM ，△AHC ≌△GNA ，从而可以得到EM =GN ，MN =4，再根据△EMI ≌△CNI 可得MI =NI =2，即可确定AI 的长度；【解题过程】(1)证明：∵BD ⊥直线l ，CE ⊥直线l ，∴∠BDA =∠CEA =90°，∵∠BAC =90°，∴∠BAD +∠CAE =90°，∵∠BAD +∠ABD =90°，在△ADB和△CEA中，∠ABD=∠CAE ∠BDA=∠CEA AB=AC，∴△ADB≌△CEA AAS∴BD=AE，AD=CE，∴DE=AE+AD=BD+CE；(2)∵BD⊥直线l，CE⊥直线l，∴∠BDA=∠CEA=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°，∴∠CAE=∠ABD，在△ADB和△CEA中，∠ABD=∠CAE ∠BDA=∠CEA AB=AC，∴△ADB≌△CEA AAS∴BD=AE，AD=CE，∴DE=AE-AD=BD-CE；(3)如图，过E作EM⊥HI于M，GN⊥HI的延长线于N，∴∠EMI=∠GNI=90°∵∠BAH+∠EAM=90°，∠BAH+∠ABH=90°，∴∠EAM=∠ABH在△ABH和△EAM中，∠AHB=∠EMA ∠ABH=∠EAM AB=AE，∴△ABH≌△EAM(AAS)∴BH=AM=3，AH=EM，同理可得：△AHC≌△GNA∴CH=AN=7，AH=GN，即：EM=GN，MN=AN-AM=7-3=4，在△EMI和△CNI中，∠EMI=∠CNI∠EIM=∠CINEM=CN，∴△EMI≌△CNI(AAS)，∴MI=NI=12MN=2，∴AI=AM+MI=3+2=5．14.(23-24八年级上·河北石家庄·阶段练习)通过对如图数学模型的研究学习，解决下列问题：(1)如图1，∠BAD=90°，AB=AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D．又∠ACB=∠AED=90°，可以推理得到△ABC≌△DAE．进而得到AC=，BC=AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；(2)如图2，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接BC,DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；(3)如图3，已知四边形ABCD和DEGF为正方形，△AFD的面积为S1，△DCE的面积为S2，S1+S2= 10．求出S1的值．【思路点拨】(1)由△ABC≌△DAE即可求解；(2)作DM⊥AF,EN⊥AF，利用“K字模型”的结论可得△ABF≌△DAM,△ACF≌△EAN，故可推出DM =EN，再证△DMG≌△ENG即可；(3)作PQ⊥CE,AM⊥PQ,FN⊥PQ，利用“K字模型”的结论可得△ADM≌△DCP,△DFN≌△EDP，进一步可证△AMQ≌△FNQ，即可求解．【解题过程】(1)解：∵△ABC≌△DAE∴AC=DE故答案为：DE；(2)证明：作DM⊥AF,EN⊥AF由“K字模型”可得：△ABF≌△DAM,△ACF≌△EAN∴AF=DM,AF=EN∴DM=EN∵∠DMG=∠ENG=90°,∠DGM=∠BGN∴△DMG≌△ENG∴GM=GN即：点G是DE的中点(3)解：作PQ⊥CE,AM⊥PQ,FN⊥PQ，如图：21∵四边形ABCD 和四边形DEGF 均为正方形∴∠ADC =∠EDF =90°,AD =CD ,DE =DF由“K 字模型”可得：△ADM ≌△DCP ,△DFN ≌△EDP∴S △ADM =S △DCP ,S △DFN =S △EDPAM =DP ,FN =DP∵∠AMQ =∠FNQ =90°,∠AQM =∠FQN∴△AMQ ≌△FNQ∴S △AMQ =S △FNQ∴S △ADQ +S △FNQ +S △DFN =S △ADQ +S △AMQ +S △DFN =S △ADM +S △DFN =S △DCP +S △EDP即：S 1=S 2∵S 1+S 2=10∴S 1=515.(23-24七年级下·广东深圳·期末)【材料阅读】小明在学习完全等三角形后，为了进一步探究，他尝试用三种不同方式摆放一副三角板(在△ABC 中，∠ABC =90°，AB =CB ；△DEF 中，∠DEF =90°，∠EDF =30°)，并提出了相应的问题．【发现】(1)如图1，将两个三角板互不重叠地摆放在一起，当顶点B 摆放在线段DF 上时，过点A 作AM ⊥DF ，垂足为点M ，过点C 作CN ⊥DF ，垂足为点N ，①请在图1找出一对全等三角形，在横线上填出推理所得结论；∵∠ABC =90°，∴∠ABM +∠CBN =90°，∵AM ⊥DF ，CN ⊥DF ，∴∠AMB =90°，∠CNB =90°，∴∠ABM +∠BAM =90°，∴∠BAM =∠CBN ，∵∠BAM=∠CBN∠AMB=∠CNB=90°AB=BC，；②AM=2，CN=7，则MN=；【类比】(2)如图2，将两个三角板叠放在一起，当顶点B在线段DE上且顶点A在线段EF上时，过点C作CP⊥DE，垂足为点P，猜想AE，PE，CP的数量关系，并说明理由；【拓展】(3)如图3，将两个三角板叠放在一起，当顶点A在线段DE上且顶点B在线段EF上时，若AE= 5，BE=1，连接CE，则△ACE的面积为．【思路点拨】本题综合考查了全等三角形的判定与性质，熟记相关定理内容进行几何推理是解题关键．(1)①根据两个三角形全等的判定定理，结合已知求证即可得到答案；②由①中△ABM≌△BCN(AAS)，利用两个三角形全等的性质，得到AM=BN=2，BM=CN=7，即可得到MN=MB+BN=CN+AM=9；(2)根据两个三角形全等的判定定理，得到△ABE≌△BCP，利用两个三角形全等的性质，得到AE=BP，BE=CP，由图中BE=BP+PE，即可得到三者的数量关系；(3)延长FE，过点C作CP⊥FE于P，如图所示，由两个三角形全等的判定定理得到△ABE≌△BCP，从而PC=BE=1，PB=AE=5，则可求得PE，延长AE，过点C作CF⊥AE于F，如图所示，由平行线间的平行线段相等可得CF=PE=4，代入面积公式得S△ACE，即可得到答案．【解题过程】解：(1)①∵∠ABC=90°，∴∠ABM+∠CBN=90°，∵AM⊥DF，CN⊥DF，∴∠AMB=90°，∠CNB=90°，∴∠ABM+∠BAM=90°，∴∠BAM=∠CBN，∵∠BAM=∠CBN，∠AMB=∠CNB=90°，AB=BC，∴△ABM≌△BCN(AAS)；故答案为：△ABM≌△BCN(AAS)②由①知△ABM≌△BCN(AAS)，∴AM=BN,BM=CN，∵AM=2，CN=7，∴MN=MB+BN=CN+AM=9；故答案为：9；(2)结论：PE=PC-AE．理由如下：∵∠ABC=90°，∴∠ABE+∠CBE=90°，∵CP⊥BE，∴∠CPB=90°，∴∠BCP+∠CBP=90°∴∠ABE=∠BCP，2223∵∠AEB =90°，∴∠AEB =∠CPB =90°，∵AB =BC ，∴△ABE ≌△BCP ，∴AE =BP ，BE =CP∵BE =BP +PE ，∴PE =BE -BP =PC -AE ；(3)延长FE ，过点C 作CP ⊥FE 于P ，如图所示：∵∠ABE +∠EBC =90°，∠ABE +∠BAE =90°，∴∠EBC =∠BAE ，∵∠AEB =∠CPB =90°，AB =BC ，∴△ABE ≌△BCP ，∴PC =BE =1，PB =AE =5，∴PE =PB -BE =5-1=4，延长AE ，过点C 作CF ⊥AE 于F ，如图所示：∵AF ⊥PE ，CP ⊥PE ，∴AF ∥CP ，∵AF ⊥PE ，CF ⊥AF ，∴PE ∥CF ，由平行线间的平行线段相等可得CF =PE =4，S △ACE =12×AE ×CF =12×5×4=10．故答案为：10．。

全等三角形中常见的辅助线的作法全等三角形问题中最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等，本节来介绍下在全等三角形中常见的几种辅助线的作法：图中有角平分线，可向两边作垂线。

线段垂直平分线，常向两端把线连。

线段计算和与差，巧用截长补短法。

三角形里有中线，延长中线至两倍。

在作辅助线的时候要注意以下两点：①在原图形中作辅助线要用“虚线”；②在证明过程中要描述添加方法。

一、用角平分线的性质构造全等例1、如图,在四边形ABCD 中, ∠A= ∠D =90°, BE、CE 分别是∠B 和∠C 的角平分线。

求证：BC= AB + CD。

证明：过点E 作EF⊥BC ，垂足为点F∵BE 是∠B 的角平分线，∠EFB = ∠A = 90°∴EF = AE在△EFB 和△EAB 中∵∠EFB = ∠A = 90°，EF = AE ，EB = EB∴△EFB ≌△EAB （HL）∴BF = BA同理可证：CF = CD∴BC = CF + BF = AB + CD二、连接法例题2、如图,在五边形ABCDE中，点M 是CD 的中点，AB = AE , BC = ED ，AM⊥CD 。

求证：∠B = ∠E 。

连接AC ，AD∵点M 是CD 的中点，AM⊥CD∴AC = AD在△ABC 和△AED 中∵AB = AE , BC = ED，AC = AD∴△ABC ≌△AED （SSS）∴∠B = ∠E三、用“截长法”或“补短法”构造全等三角形例题3、如图，在△ABC中，AD是∠BAC的角平分线，∠C = 2∠B 。

求证：AB = AC + CD 。

证明：方法一、截长法在线段AB 上取点E ，使得AE = AC , 连接ED∵AD是∠BAC的角平分线∴∠EAD = ∠CAD在△EAD 和△CAD 中∵AE = AC , ∠EAD = ∠CAD ，AD = AD∴△EAD ≌△CAD∴ED = CD , ∠AED = ∠ACD又∵∠AED = ∠B + ∠EDB （三角形外角和定理），∠ACD = 2∠B∴∠B + ∠EDB = 2∠B （等量代换）∴∠B = ∠EDB∴BE = ED （等角对等边）又∵AB = AE + EB∴AB = AC + CD （等量代换）方法二、补短法延长线段AC 至点 F ，使CF = CD ，连接DF略证：由∠ACB = 2∠B = ∠CDF + ∠F ，∠CDF = ∠F可得∠B = ∠F在证△ABD ≌△AFD （AAS）可得AB = AF而AF = AC + CF = AC + CD即证AB = AC + CD注：遇到有二条线段长之和等于第三条线段的长，常用此方法。

专项练习(五)证明三角形全等四种添加辅助线的方法►方法一直接连线构造全等三角形1．如图5－ZT－1所示，AB＝AD，BC＝DC.求证：∠ABC＝∠ADC.图5－ZT－12．如图5－ZT－2，AB＝AE，∠ABC＝∠AED，BC＝ED，AF⊥CD.求证：F是CD的中点．图5－ZT－23．如图5－ZT－3，AC，BD相交于点O，且AB＝DC，AC＝DB.求证：∠ABO＝∠DCO.图5－ZT－3►方法二倍长中线构造全等三角形4．如图5－ZT－4，AD是△ABC的边BC上的中线，AB＝4，AC＝8，求中线AD的取值范围．图5－ZT－45．如图5－ZT－5，CE，CB分别是△ABC，△ADC的中线，且AB ＝AC.求证：CD＝2CE.(提示：等腰三角形的两底角相等)图5－ZT－5►方法三作垂直构造全等三角形6．如图5－ZT－6，四边形ABCD中，BC＜BA，AD＝CD，BD平分∠ABC.求证：∠A＋∠C＝180°.图5－ZT－67．如图5－ZT－7，∠AOB＝90°，OM平分∠AOB，将直角三角板的顶点P在射线OM上移动，两直角边与OA，OB分别交于点C，D，PC 与PD相等吗？试说明理由．图5－ZT－7►方法四翻折构造全等三角形8．如图5－ZT －8所示，BE 平分∠ABC ，E 为AD 的中点，且BC ＝B A ＋CD.求证：CE 平分∠BCD.图5－ZT －89．2019·南京二模命题：有两个角相等的三角形是等腰三角形(简称〝等角对等边〞)．：如图5－ZT －9，△ABC 中，∠B ＝∠C.求证：AB ＝AC.三名同学作出了三种不同的辅助线，并完成了命题的证明．小刚的方法：作∠BAC 的平分线AD ，可证△ABD ≌△ACD ，得AB ＝AC ；小亮的方法：作BC 边上的高AD ，可证△ABD ≌△ACD ，得AB ＝AC ；小莉的方法：作BC 边上的中线AD.(1)请你写出小刚与小亮的方法中△ABD ≌△ACD 的理由：________________；(2)请你按照小莉的思路完成命题的证明．图5－ZT －9详解详析1．证明：连接AC ， 在△ABC 与△ADC 中，∵⎩⎪⎨⎪⎧AB ＝AD ，BC ＝DC ，AC ＝AC ，∴△ABC ≌△ADC ，(SSS) ∴∠ABC ＝∠ADC.2．证明：如图，连接AC ，AD. 在△ABC 和△AED 中，∵⎩⎪⎨⎪⎧AB ＝AE ，∠ABC ＝∠AED ，BC ＝ED ，∴△ABC ≌△AED ，(SAS) ∴AC ＝AD.∵AF ⊥AD ，∴∠AFC ＝∠AFD ＝90°.在Rt △ACF 和Rt △ADF 中， ∵⎩⎪⎨⎪⎧AC ＝AD ，AF ＝AF ， ∴Rt △ACF ≌Rt △ADF ，(HL)∴CF ＝DF ，∴F 是CD 的中点．3．证明：连接BC. 在△ABC 和△DCB 中，∵⎩⎪⎨⎪⎧AB ＝DC ，AC ＝DB ，BC ＝CB ，∴△ABC ≌△DCB ，(SSS) ∴∠ABC ＝∠DCB ，∠ACB ＝∠DBC ，∴∠ABC －∠DBC ＝∠DCB －∠ACB ，即∠ABO ＝∠DCO.4．[解析] 通过作辅助线，把AB ，AD ，AC 转化到同一个三角形中，如图，证△ADB ≌△EDC ，推出EC ＝AB ，在△ACE 中，利用三角形的三边关系求解．解：如图，延长AD 到点E ，使AD ＝DE ，连接CE.∵D 是BC 的中点，∴BD ＝CD. 在△ADB 和△EDC 中，∵⎩⎪⎨⎪⎧AD ＝ED ，∠ADB ＝∠EDC ，BD ＝CD ，∴△ADB ≌△EDC ，(SAS) ∴EC ＝AB ＝4，∴AC －EC ＝AC －AB ＝8－4＝4，AC ＋EC ＝AC ＋AB ＝12.在△ACE 中，根据三角形的三边关系，得4<AE<12.∵AE ＝2AD ，∴2<AD<6.5．证明：延长CE 到点F ，使EF ＝CE ，连接FB.∵CE 是△ABC 的中线，∴AE ＝EB. 在△AEC 和△BEF 中，∵⎩⎪⎨⎪⎧AE ＝EB ，∠AEC ＝∠BEF ，CE ＝EF ，∴△AEC ≌△BEF ，(SAS) ∴∠A ＝∠EBF ，AC ＝BF.∵AB ＝AC ，∴∠ABC ＝∠ACB ，∴∠CBD ＝∠A ＋∠ACB ＝∠EBF ＋∠ABC ＝∠CBF.∵CB 是△ADC 的中线，∴AB ＝BD ，又∵AB ＝AC ，AC ＝BF ，∴BF ＝BD. 在△CBF 和△CBD 中，∵⎩⎪⎨⎪⎧BF ＝BD ，∠CBF ＝∠CBD ，CB ＝CB ，∴△CBF ≌△CBD ，(SAS) ∴CD ＝CF ＝CE ＋EF ＝2CE.6．证明：如图，过点D 作DE ⊥BA 于点E ，DF ⊥BC 交BC 的延长线与点F.∵BD 平分∠ABC ，∴∠DBE ＝∠DBF.∵DE ⊥AB ，DF ⊥BC ，∴∠BED ＝∠BFD ＝90°. 在△DBE 和Rt △DBF 中，∵⎩⎪⎨⎪⎧∠BED ＝∠BFD ，∠DBE ＝∠DBF ，BD ＝BD ， ∴△DBE ≌△DBF ，(AAS)∴DE ＝DF. 在Rt △DEA 和Rt △DFC 中，∵⎩⎪⎨⎪⎧AD ＝CD ，DE ＝DF ， ∴Rt △DEA ≌Rt △DFC ，(HL)∴∠A ＝∠DCF.∵∠BCD ＋∠DCF ＝180°，∴∠A ＋∠BCD ＝180°.7．解：PC 与PD 相等．理由如下：过点P 作PE ⊥OA 于点E ，PF ⊥OB 于点F.∵OM 平分∠AOB ，∴∠POE ＝∠POF. 在△OPE 与△OPF 中，∵⎩⎪⎨⎪⎧∠OEP ＝∠OFP ，∠POE ＝∠POF ，OP ＝OP ，∴△OPE ≌△OPF ，(AAS)∴PE ＝PF.∵∠AOB ＝90°，∠PEO ＝∠PFO ＝90°，∴∠EPF ＝90°，∴∠EPC ＋∠CPF ＝90°.又∵∠CPD ＝90°，∴∠CPF ＋∠FPD ＝90°，∴∠EPC ＝∠FPD ＝90°－∠CPF. 在△PCE 与△PDF 中，∵⎩⎪⎨⎪⎧∠PEC ＝∠PFD ，PE ＝PF ，∠EPC ＝∠FPD ，∴△PCE ≌△PDF ，(ASA)∴PC ＝PD.8．[解析] 在BC 上截取BF ＝BA.根据SAS 证明△BAE ≌△BFE ，再证明△CEF ≌△CED 即可．证明：如图，在BC 上截取BF ＝BA ，连接EF.∵BE 平分∠ABC ，∴∠ABE ＝∠FBE. 在△BAE 和△BFE 中，∵⎩⎪⎨⎪⎧BA ＝BF ，∠ABE ＝∠FBE ，BE ＝BE ，∴△BAE ≌△BFE ，(SAS)∴AE ＝FE.∵E 是AD 的中点，∴DE ＝AE ＝FE.又∵BC ＝BA ＋CD ，BA ＝BF ，∴CD ＝CF. 在△CED 和△CEF 中，⎩⎪⎨⎪⎧CD ＝CF ，DE ＝FE ，CE ＝CE ，∴△CED ≌△CEF ，(SSS) ∴∠FCE ＝∠DCE ，即CE 平分∠BCD.9．解：(1)AAS(2)证明：过点D 作DE ⊥AB 于点E ，DF ⊥AC 于点F.∵AD 是BC 边上的中线，∴BD ＝CD.在△BDE 和△CDF 中， ∵⎩⎪⎨⎪⎧∠BED ＝∠CFD ＝90°，∠B ＝∠C ，BD ＝CD ， ∴△BDE ≌△CDF ，(AAS)∴BE ＝CF ，DE ＝DF. 在Rt △AED 和Rt △AFD 中，∵⎩⎪⎨⎪⎧AD ＝AD ，DE ＝DF ， ∴Rt △AED ≌Rt △AFD ，(HL)∴AE ＝AF ，∴AE ＋BE ＝AF ＋CF ，即AB ＝AC.。