经典文档1、五点法作图的步骤

尺规作图五点定椭圆的方法徐文平（东南大学南京210096）摘要：已知椭圆上五点，通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤，尺规作图完成椭圆作图。

椭圆在开普勒行星运行三定律中扮演了重要角色，在机械制图和土木工程领域中也有重要运用。

利用几何画板和cad软件，依据任意五个点的椭圆尺规作图，具有重要意义。

一、引言在几何画板和cad软件中，任意五个点作椭圆，具有意义。

五点定椭圆在卫星轨道，机械制图和土木工程中是有重要用途。

第一步，通过五点寻找椭圆圆心第二步，确定椭圆坐标x、y主轴方向第三步、确定椭圆的长轴a和短轴b1）大狗熊定理1：二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。

如图1，椭圆内接四边形KLMN，对边线KN与LM交于A，对边线KL与NM交于B，对角线KM的极点为C，对角线LN的极点为D，KM与LN交于Q点，则A、B、C、D四点共线，且AB调和分割CD，即1/AC+1/AD＝2/AB。

双曲线和抛物线也具有同样性质。

2）命题1：已知椭圆的斜向割线AB，作一条过椭圆圆心O点的任意割线JK，JA、BK交于E点，JB、AK交于F点，确定EF的中点N点，连线NA、NB就是椭圆的切线。

证明：由于割线JK的切线交点极点在无穷远，利用定理1，可以快速证明这个命题。

定理2：圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。

命题3（高斯定理）：已知椭圆外一点P，过P点作PAB与PCD二条任意椭圆割线，AD、CB交于Q点，AC、BD延长交于R，连线QR与椭圆交于S、T两点，PS、PT就是椭圆的切线。

图 3二、通过五点寻找椭圆圆心原理：通过已知五点，作椭圆切线，获得割线的极点，将割线的极点和割线中点连接并延伸，必定通过椭圆的圆心。

图 4问题1：只有五点，没有坐标轴和原点，椭圆斜的，割线PQ的切线极点如何办？切线方法：帕斯卡定理（五点+ 一个切点二次）做切线，或者如图5方法作切线。

5.4.1 正弦函数、余弦函数的图象一、正弦函数、余弦函数图象的画法1．描点法：按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法． 2．几何法：利用三角函数线作出正弦函数和余弦函数在]2,0[π内的图象，再通过平移得到x y sin =和cos y x =的图象．3．五点法：先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点，再利用光滑曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象．在确定正弦函数x y sin =在]2,0[π上的图象时，关键的五点是：)0,2(),1,23(),0,(),1,2(),0,0(ππππ-【注意】（1）若x R ∈，可先作出正弦函数、余弦函数在]2,0[π上的图象，然后通过左、右平移可得到x y sin =和cos y x =的图象．（2）由诱导公式cos sin()2y x x π==+，故cos y x =的图象也可以将x y sin =的图象上所有点向左平移2π个单位长度得到． 二、正（余）弦函数的图象 函数y ＝sin xy ＝cos x图象图象画法五点法五点法关键五点 (0,0),π(,1)2,(,0)π,3π(,1)2-,(2,0)π (0,1),π(,0)2,(,1)π-,3π(,0)2,(2,1)π正（余）弦曲线正（余）弦函数的图象叫做正（余）弦曲线三、用三角函数图象解三角不等式的方法1、作出相应正弦函数或余弦函数在[0,2π]上的图象；2、写出适合不等式在区间[0,2π]上的解集；3、根据公式一写出不等式的解集．题型一 五点法作三角函数的图象【例1】用“五点法”作y ＝2sin2x 的图象，首先描出的五个点的横坐标是（ ） A ．30,,,,222ππππ B ． 30,,,,424ππππ C ．0,,2,3,4ππππD ．20,,,,6323ππππ【答案】B【解析】由“五点法”作图知：令2x ＝0，2π，π，32π，2π，解得x ＝0，4π，2π，34π，π，即为五个关键点的横坐标，故选：B.【变式1-1】用“五点法”作函数cos 1y x =-，[]0,2x π∈的大致图像，所取的五点是______．【答案】(0,0)，,12π⎛⎫- ⎪⎝⎭，(,2)π-，3,12π⎛⎫- ⎪⎝⎭，(2,0)π【解析】由“五点法”作函数cos 1y x =-，[0x ∈，2]π的图象时的五个点分别是(0,0)，,12π⎛⎫- ⎪⎝⎭，(,2)π-，3,12π⎛⎫- ⎪⎝⎭，(2,0)π．【变式1-2】用“五点法”画出下列函数的简图：（1）cos 1y x =-，[],x ππ∈-； （2）sin y x =，3,22x ππ⎡⎤∈-⎢⎥⎣⎦； （3）sin y x =-，[]0,2x π∈．【答案】（1）见解析；（2）见解析；（3）见解析 【解析】（1）按五个关键点列表xπ-2π-2ππcos x1-0 11cos 1x -2- 1- 01- 2-（2）按五个关键点列表x2π-0 2ππ32πsin x1- 011-描点并将它们用光滑的曲线连接起来如下图（3）按五个关键点列表x0 2ππ32π2πsin x11-sin x -0 1-0 1 0【变式1-3】用“五点法”作下列函数的简图. （1）2sin ([0,2])y x x π=∈；（2）5sin()([,])222y x x πππ=-∈. （3）2sin(2)3y x π=-(x ∈R ).【答案】（1）图象答案见解析；（2）图象答案见解析；（3）图象答案见解析. 【解析】（1）列表如下：x2ππ 32π2π 2sin x 02 0 -2 0描点连线如图：（2）列表如下：x2ππ 32π2π 52πsin()2x π-0 1 0 -1 0（3）函数π2sin 23y x ⎛⎫=- ⎪⎝⎭在长为一个周期π的区间上的图象，列表如下：x6π512π23π1112π76π23x π-0 2ππ32π2πy 02 0 -2 0再向左右两边扩展，其图象如下：题型二 含绝对值的三角函数【例2】函数y ＝|cos x |的一个单调增区间是（ ）A ．,22ππ⎡⎤-⎢⎥⎣⎦B ．[0，π]C ．3,2ππ⎡⎤⎢⎥⎣⎦D ．3,2π2π⎡⎤⎢⎥⎣⎦【答案】D【解析】将y ＝cos x 的图像位于x 轴下方的图像关于x 轴对称翻折到x 轴上方，x 轴上方(或x 轴上)的图像不变，即得y ＝|cos x |的图像根据各选项判断只有D 选项正确. 故选：D.【变式2-1】作出函数2sin sin y x x =+，[],x ππ∈-的大致图像． 【答案】图见解析【解析】函数[][]3sin ,0,2sin sin sin ,,0x x y x x x x ππ⎧∈⎪=+=⎨-∈-⎪⎩， 其图如下所示：【变式2-2】作出函数sin ||,[2,2]=∈-y x x ππ的大致图像. 【答案】图象见解析 【解析】列表x0 2ππ32π2πsin ||y x =1 0 -1 0作图：先作出(]0,2π的图像，又原函数是偶函数,图像关于y 轴对称， 即可作出[)2,0π-的图像.【变式2-3】作函数3sin 2y x π⎛⎫=+ ⎪⎝⎭的图象.【答案】图象见解析.【解析】3sin cos 2y x x π⎛⎫=+= ⎪⎝⎭ cos 22,Z 223cos 22,Z 22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象，如图题型三 三角函数识图问题【例3】函数1sin =+y x x的大致图象是（ ）A ．B ．C ．D ．【答案】A【解析】函数1sin =+y x x是定义域(,0)(0,)-∞+∞上的奇函数∴其图象关于原点对称，排除选项D ；当(0,)x π∈时，sin 0x >，此时1sin 0x x+>，∴当(0,)x π∈时，()f x 的图象在x 轴上方，排除选项B ； 当32x π=时，322sin 10233πππ+=-+<，()f x 的图象在x 轴下方，排除选项C ；综上所述，函数1sin =+y x x的大致图象为选项A .故选：A .【变式3-1】函数2sin 2xy x =-的图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】令0x =，则02sin 01y =-=，排除C 、D ；令1x =-，则()112sin 2sin 202y -=--=+>，排除B.故选：A【变式3-2】已知函数()y f x =的图象如图所示，则此函数可能是（ ）A ．()sin ln ||f x x x =⋅B ．()sin ln ||f x x x =-⋅C ．()sin ln f x x x =⋅D ．()|sin ln |f x x x =⋅ 【答案】A【解析】图象关于原点对称，为奇函数，CD 中定义域是0x >，不合，排除，AB 都是奇函数，当(0,1)x ∈时，A 中函数值为负，B 中函数值为正，排除B ．故选：A ．【变式3-3】已知函数()f x 的部分图象如图所示，则()f x 的解析式可能为（ ）A ．()sin πf x x x =B ．()(1)sin πf x x x =-C ．[]()cos π(1)f x x x =+D ．()(1)cos πf x x x =- 【答案】B【解析】对于A ，()()sin πsin π()f x x x x x f x -=--==，所以函数()sin πf x x x =为偶函数，故排除A ； 对于D ，()010f =-≠，故排除D ；对于C ，[]()cos π(1)cos πf x x x x x =+=-，则()()cos πf x x x f x -==-， 所以函数[]()cos π(1)f x x x =+为奇函数，故排除C.故选：B.题型四 利用图象解三角不等式【例4】不等式2sin ,(0,2)2xx π∈的解集为（ ） A ．,62ππ⎡⎤⎢⎥⎣⎦ B ．3,44ππ⎡⎤⎢⎥⎣⎦ C ．423,ππ⎡⎤⎢⎥⎣⎦ D ．,64ππ⎡⎤⎢⎥⎣⎦【答案】B 【解析】2sin ,(0,2)2xx π∈ sin y x =函数图象如下所示：∴344ππ≤≤x ，∴不等式的解集为：3,44ππ⎡⎤⎢⎥⎣⎦．故选：B ．【变式4-1】在()0,2x π∈上，满足cos sin x x >的x 的取值范围（ ）A ．5,44ππ⎛⎫ ⎪⎝⎭B ．0,4π⎛⎫ ⎪⎝⎭C ．50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ D ．5,24ππ⎛⎫⎪⎝⎭【答案】C【解析】作出sin y x =和cos y x =在()0,2x π∈的函数图象，根据函数图象可得满足cos sin x x >的x 的取值范围为50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭.故选：C.【变式4-2】在[]0,2π内，不等式3sin x < ） A ．(0，π) B ．3,34ππ⎛⎫ ⎪⎝⎭C ．45,33ππ⎛⎫ ⎪⎝⎭ D ．5,23ππ⎛⎫⎪⎝⎭【答案】C【解析】画出y ＝sin x ，[]0,2x π∈的草图如下．[]0,2x π∈内，令3sin x =43x π=或53x π=，结合图象可知不等式3sin x <的解集为45,33ππ⎛⎫ ⎪⎝⎭．故选：C ．【变式4-3】若函数()2sin13f x x π=- ）A ．56,622k k ππππ⎡⎤++⎢⎥⎣⎦（k ∈Z ） B ．156,622k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ）C ．56,644k k ππππ⎡⎤++⎢⎥⎣⎦（k ∈Z ） D ．156,644k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ） 【答案】B【解析】要使函数有意义，则2sin103x π-≥，即1sin32x π≥， 即522636k x k πππππ+≤≤+，k ∈Z ，得156622k x k +≤≤+，k ∈Z ， 即函数的定义域为156,622k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ）.故选：B【变式4-4】已知()f x 的定义域是3⎡-⎢⎣⎦，则(sin 2)f x 的定义域为（ ） A ．2,36k k ππππ⎡⎤-++⎢⎥⎣⎦，k Z ∈ B ．,63k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈C ．22,236k k ππππ⎡⎤-++⎢⎥⎣⎦，k Z ∈ D ．2,263k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈【答案】A 【解析】()f x 的定义域是3⎡-⎢⎣⎦，故由31sin 2x -≤≤解得()422233k x k k Z ππππ-+≤≤+∈， ()236k x k k Z ππππ∴-+≤≤+∈ 因此，函数(sin 2)f x 的定义域为()22,236k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.故选：A.【变式4-5】函数y 12log sin x________． 【答案】{}22,x k x k k Z πππ<<+∈ 【解析】由1122log sin 0log 1x ≥=知，0sin 1x <≤，由正弦函数图象特征知，22,k x k k Z πππ<<+∈． 故定义域为{}22,x k x k k Z πππ<<+∈. 故答案为：{}22,x k x k k Z πππ<<+∈.题型五 与正余弦函数有关的零点【例5】函数sin y x =，[]0,2πx ∈的图像与直线23y =-的交点的个数为（ ） A ．0 B ．1 C ．2 D ．3 【答案】C【解析】在同一平面直角坐标系内，先画函数sin y x =，[]0,2πx ∈的图像，再画直线23y =-，可知所求交点的个数为2．故选：C ．【变式5-1】已知函数f (x )=12x⎛⎫⎪⎝⎭-sin x ，则f (x )在区间[0，2π]上的零点个数为（ ）A ．1B ．2C ．3D ．4 【答案】B【解析】令sin 01()2xf x x ⎛⎫-=⎪⎝⎭= ，则1()sin 2x x =， 在同一坐标系中，作出1(),sin 2xy y x ==，如下图所示：由图知，f (x )在区间[0，2π]上的零点个数为2个.故选：B.【变式5-2】()f x 是定义在R 上的偶函数，且()()11f x f x -=+，[]1,0x ∈-时，()sin 2f x x ππ⎛⎫=+⎪⎝⎭，则函数()()e x g x f x -=-在区间[]2021,2022-上零点的个数为（ ）A ．2021B ．4043C ．2020D ．4044 【答案】B 【解析】(1)(1)f x f x -=+，()(2)f x f x ∴=+，即函数()f x 的周期为2，当[]1,0x ∈-时，()sin()sin()22f x x x πππ=+=-，则当[]0,1x ∈时，()()sin()sin()22f x f x x x ππ=-=--=， 由此可作出函数()f x 与函数e -=xy 的大致图象如下，由图象可知，每个周期内有两个交点， 所以函数((e))xg x f x -=-在区间[]2021,2022-上零点的个数为2021214043⨯+=个．故选：B ．【变式5-3】函数()sin 3|sin |,[0,2]f x x x x π=+∈的图象与直线y k =有且仅有两个不同的交点，则k 的取值范围是（ ）A ．[2,2]-B ．(1,0)(0,3)-C ．(2,4)D ．(1,4) 【答案】C【解析】当[0,]x π∈时，()sin 3sin 4sin f x x x x =+=，当(],2x ππ∈时，()sin 3sin 2sin f x x x x =+=-， 所以函数()f x 的图像如图所示，所以函数()f x 的图象与直线y k =有且仅有两个不同的交点时，(2,4)k ∈.故选：C【变式5-4】已知函数()1sin ,0,21cos ,0,2x x f x x x ⎧+<⎪⎪=⎨⎪+≥⎪⎩若()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点，()f x 在区间[],a π-上至多有5个零点，则正数a 的取值范围是（ ）A ．138,63ππ⎡⎤⎢⎥⎣⎦ B ．1310,63ππ⎡⎫⎪⎢⎣⎭ C ．1910,63ππ⎡⎫⎪⎢⎣⎭ D ．819,36ππ⎡⎤⎢⎥⎣⎦【答案】B【解析】因为方程1sin 2x =-在[),0π-上的解为56π-，6π-， 所以当()f x 在区间[],a π-上至多有5个零点时，100.3a π<<因为方程1cos 2x =-在30,2π⎡⎤⎢⎥⎣⎦上的解为23π，43π， 所以当()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点时，136a π-≤-，即136a π≥综上，正数a 的取值范围是1310,63ππ⎡⎫⎪⎢⎣⎭，故选：B。

五点作图教案教案标题：五点作图教案教学目标：1.学生能够理解并应用作图的基本概念和技巧。

2.学生能够使用五个给定的点在平面直角坐标系中绘制图形。

3.学生能够通过观察和分析已有的图形，推导出作图规律。

教学准备：1.平面直角坐标系的模型或投影仪。

2.五个标记好的点（可用彩色贴纸或小纸片标记）。

3.白板、白板笔、橡皮擦。

4.练习纸和铅笔。

教学过程：引入：1.通过展示平面直角坐标系的模型或投影仪，向学生介绍坐标系的概念和基本结构。

2.解释五点作图的概念，即使用五个给定的点在坐标系中绘制图形。

探究：1.给出五个标记好的点，并要求学生按照给定的顺序在坐标系中绘制图形。

2.引导学生观察和分析已绘制的图形，让他们发现图形之间的规律。

3.鼓励学生尝试不同的顺序和位置来绘制图形，以加深对作图规律的理解。

实践：1.提供一系列的作图练习，要求学生根据给定的五个点在坐标系中绘制图形。

2.逐步增加练习的难度，例如增加点的数量或要求绘制更复杂的图形。

3.鼓励学生思考和讨论不同的解决方法，以促进他们的创造力和批判性思维能力。

总结：1.复习并总结学生在本课程中学到的作图规律和技巧。

2.与学生一起回顾他们在探究和实践环节中的学习成果。

3.提醒学生在未来的学习中应用作图技巧，解决实际问题。

拓展：1.提供更多的作图练习，让学生进一步巩固所学的知识和技能。

2.引导学生思考如何将作图技巧应用到其他学科或实际生活中。

评估：1.观察学生在课堂上的参与度和作图的准确性。

2.布置作业，要求学生完成额外的作图练习，并对其进行评估。

3.根据学生的表现和理解程度，提供个别指导和反馈。

教学延伸：1.引导学生探索更高级的作图技巧，如使用曲线和不规则形状进行作图。

2.鼓励学生设计自己的作图练习，并与同学分享。

教学资源：1.平面直角坐标系的模型或投影仪。

2.五个标记好的点。

3.白板、白板笔、橡皮擦。

4.练习纸和铅笔。

教学反思：在教学过程中，我会密切观察学生的学习情况，并根据需要进行灵活调整。

新华爱心高级中学高一数学 高一（ ） 姓名： 时间：
1.1.1五点法作图
学习目标：会用五点法作图
完成下列题目：
例题一：（1）用五点法作出 y=sinx,

0,2x
的图象

用五点法作出y=cosx, 0,2x的图象
（2）看图像解题
1、根据函数y=sinx的图像，可知当263,x时，函数的最大值是 ，最小值
是

2、结合图像，关于方程8cosxx的零点有 个。
练习： 结合图象，判断方程xsinx的实数解的个数
练习：1、画出 cos1yx 的图象

/

x
sinx

x
cosx
新华爱心高级中学高一数学 高一（ ） 姓名： 时间：
2、画出cosyx的图像

例题二：（1）画出sin3yx 和 sin3yx 的图象
sin3yx




sin3yx



新华爱心高级中学高一数学 高一（ ） 姓名： 时间：
练习：1、书本P34 1、2
2、
画出下列函数的简图：(1) y=|sinx|， （2）y=sin|x|

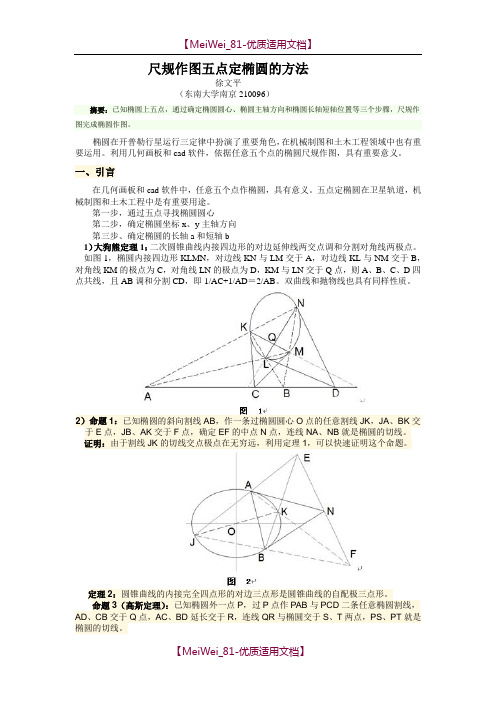
尺规作图五点定椭圆的方法徐文平（东南大学南京210096）摘要：已知椭圆上五点，通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤，尺规作图完成椭圆作图。

椭圆在开普勒行星运行三定律中扮演了重要角色，在机械制图和土木工程领域中也有重要运用。

利用几何画板和cad软件，依据任意五个点的椭圆尺规作图，具有重要意义。

一、引言在几何画板和cad软件中，任意五个点作椭圆，具有意义。

五点定椭圆在卫星轨道，机械制图和土木工程中是有重要用途。

第一步，通过五点寻找椭圆圆心第二步，确定椭圆坐标x、y主轴方向第三步、确定椭圆的长轴a和短轴b1）大狗熊定理1：二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。

如图1，椭圆内接四边形KLMN，对边线KN与LM交于A，对边线KL与NM交于B，对角线KM的极点为C，对角线LN的极点为D，KM与LN交于Q点，则A、B、C、D四点共线，且AB调和分割CD，即1/AC+1/AD＝2/AB。

双曲线和抛物线也具有同样性质。

2）命题1：已知椭圆的斜向割线AB，作一条过椭圆圆心O点的任意割线JK，JA、BK交于E点，JB、AK交于F点，确定EF的中点N点，连线NA、NB就是椭圆的切线。

证明：由于割线JK的切线交点极点在无穷远，利用定理1，可以快速证明这个命题。

定理2：圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。

命题3（高斯定理）：已知椭圆外一点P，过P点作PAB与PCD二条任意椭圆割线，AD、CB交于Q点，AC、BD延长交于R，连线QR与椭圆交于S、T两点，PS、PT就是椭圆的切线。

图3二、通过五点寻找椭圆圆心原理：通过已知五点，作椭圆切线，获得割线的极点，将割线的极点和割线中点连接并延伸，必定通过椭圆的圆心。

图4问题1：只有五点，没有坐标轴和原点，椭圆斜的，割线PQ的切线极点如何办？切线方法：帕斯卡定理（五点+一个切点二次）做切线，或者如图5方法作切线。

尺规作图五点定椭圆的方法本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March尺规作图五点定椭圆的方法徐文平（东南大学南京210096）摘要：已知椭圆上五点，通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤，尺规作图完成椭圆作图。

椭圆在开普勒行星运行三定律中扮演了重要角色，在机械制图和土木工程领域中也有重要运用。

利用几何画板和cad软件，依据任意五个点的椭圆尺规作图，具有重要意义。

一、引言在几何画板和cad软件中，任意五个点作椭圆，具有意义。

五点定椭圆在卫星轨道，机械制图和土木工程中是有重要用途。

第一步，通过五点寻找椭圆圆心第二步，确定椭圆坐标x、y主轴方向第三步、确定椭圆的长轴a和短轴b1）大狗熊定理1：二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。

如图1，椭圆内接四边形KLMN，对边线KN与LM交于A，对边线KL与NM交于B，对角线KM的极点为C，对角线LN的极点为D，KM与LN 交于Q点，则A、B、C、D四点共线，且AB调和分割CD，即1/AC+1/AD＝2/AB。

双曲线和抛物线也具有同样性质。

2）命题1：已知椭圆的斜向割线AB，作一条过椭圆圆心O点的任意割线JK， JA、BK交于E点，JB、AK交于F点，确定EF的中点N点，连线NA、NB就是椭圆的切线。

证明：由于割线JK的切线交点极点在无穷远，利用定理1，可以快速证明这个命题。

定理2：圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。

命题3（高斯定理）：已知椭圆外一点P，过P点作PAB与PCD二条任意椭圆割线，AD、CB交于Q点，AC、BD延长交于R，连线QR与椭圆交于S、T 两点，PS、PT就是椭圆的切线。

图 3二、通过五点寻找椭圆圆心原理：通过已知五点，作椭圆切线，获得割线的极点，将割线的极点和割线中点连接并延伸，必定通过椭圆的圆心。

5点校准法（原创版）目录1.5 点校准法简介2.5 点校准法的应用领域3.5 点校准法的操作步骤4.5 点校准法的优点与局限性5.结论正文【5 点校准法简介】5 点校准法是一种广泛应用于测量、绘图和其他需要精确空间定位的领域的技术。

它的核心思想是利用一个已知的准确点，通过对其他点的测量和计算，来确定这些点的精确位置。

这个方法因为其操作简便、精度高，所以在各种需要精确空间定位的场景中都得到了广泛的应用。

【5 点校准法的应用领域】5 点校准法在许多领域都有应用，比如在工程测量中，可以用来测量建筑物的精确位置，确保建筑的准确性和安全性。

在制造领域，它可以用来校准机器人的精确位置，提高生产的精度。

甚至在摄影和影视制作中，也可以利用 5 点校准法来确定摄影机的精确位置，以实现特效的精确制作。

【5 点校准法的操作步骤】5 点校准法的操作步骤主要包括：首先，选择一个已知的准确点，这个点通常是已知的控制点或者是可以精确测量的位置。

然后，通过对这个点的测量，得到一个基准点。

接下来，再选择其他的点，通过对这些点的测量和计算，来确定它们的精确位置。

最后，通过校准后的点，可以得到需要测量的点的精确位置。

【5 点校准法的优点与局限性】5 点校准法的优点是操作简便，精度高，可以快速准确地确定点的位置。

然而，它也存在一些局限性，比如需要有已知的准确点，对于没有准确点的场景，就无法应用。

此外，它的精度也受到测量设备的影响，如果设备的精度不高，那么通过 5 点校准法得到的点的精度也会受到影响。

【结论】总的来说，5 点校准法是一种操作简便、精度高的空间定位技术，广泛应用于各种需要精确空间定位的领域。

正弦、余弦函数的图象——五点法作图 一、教学目标： 知识与技能：理解正弦、余弦函数图象的画法，并能熟练画出两个函数的图象；理解“五点法”作图，并能用“五点法”画出函数sinyAx的图象。 过程与方法：利用正弦线画正弦曲线、结合诱导公式得到余弦曲线；由正弦函数0,2的图象总结“五点法”，进而画函数sinyAx的图象。

情感态度价值观：学生通过作图感受数学思维的严谨性，体会学习数学的乐趣、提升学习数学自信心。 二、教学重点：“五点法”画函数sinyAx的图象。

三、教学难点：用三角函数线画正弦曲线。

四、教学过程： 1、考纲解读：同学们阅读考纲对三角函数的图像和性质的要求，教师提出问题，你是怎样理解的？在这部分的复习中，你准备怎么做？ 2、你能回忆出正弦曲线是如何得到的？试画出sin,0,2yxx的图象。

找一名同学进行板演，追问你是如何精确地描出图象上的点的？引导学生回忆三角函数线的知识。学生回答后，要给与适当的点评与鼓励，用大屏幕显示图像的生成过程。

3、通过上述图象，你能找到关键点都有哪些？能利用这些关键点作出函数sin2yx



的图象吗？这又是哪一函数的图象？它的关键点又有哪些？ 学生先自主完成，教师有一个完整的板演。然后要求学生仿照例题，完成下面的练习。 4、根据“五点法”作下列函数的简图

（1）、1sin,0,2yxx；（2）、sin23yx； （3）、2sin44yx；（4）、3sin2,0,4yxx



。

五、小结：学生总结本节内容及需要注意的问题。

六、作业：根据本节课内容，请完成：

（1）、总结正弦函数、余弦函数都有哪些性质？ （2）、画出函数tanyx的图象。 （3）、从图象的变换这一角度，总结函数sin0,0yAxA， 的图象是由正弦曲线怎样变化得到的？ （4）、完成练习册相应习题。 七、板书设计：

五点光滑法分类：GIS算法2009-12-27 16:17 575人阅读评论(4) 收藏举报由离散点绘制光滑曲线的方法—五点光滑法在GIS开发中，我们经常会遇到一些由离散点绘制光滑曲线的问题，比如用不规则三角网生成等值线，我们求出了等值线上的各个点，怎么把这些点连成一条光滑的曲线，就需要用到光滑算法。

光滑算法有很多种，比如线性跌代、分段三次多项式插值法(又称五点法)，二次多项式加权平均法、张力样条函数法等。

本文主要介绍五点法，也是用来光滑等高线的常用方法。

五点法的基本思路如下：1）每两个数据点之间建立一条三次多项式曲线方程。

2）曲线具有连续的一阶导数3）各节点的导数是以一点为中心，左右两边各相邻的两个点，一共五个点来确定的。

由条件三，我们可以认为我们已经得到了该曲线在每一个点的一阶导数（方法见后面的介绍），那么在任意两个相邻的离散点之间，我们可以得到下面四个方程：设曲线方程为y = f(x)，已求出的各点的导数为设则可由上述方程组求出a、b、c、d的值，即得到两点之间的函数表达式。

下面介绍如何根据一个点的前两点及后两点来确定该点的一阶导数值：如下图所示：图中是待一阶导数的点，AB为曲线的切线，由AKIMA条件可得：既可求出点的一阶导数。

对于第一个点和第二个点以及倒数第二个点及第一个点，采用补点的方法，来求他们的导数，补点采用增量相等的原则来补，举个例子：P0为第一个点，P1为第二个点，p2为第三点，如果我要求P1的导数，就必须补出A点，这样它的前面才会有两个点。

P0和P1的坐标已知，则由：p2p1增量-p1p0增量=p1p0增量-p0A增量可补出A点，同理补出B点，这样P0、p1的一阶导数均可用五点法求出。

5.4 三角函数的图象与性质 5.4.1 正弦函数、余弦函数的图象 课标要求 素养要求 1.能利用三角函数的定义，画y＝sin x，y＝cos x的图象. 2.掌握“五点法”画y＝sin x，y＝cos x的图象的步骤和方法，能利用“五点法”作出简单的正弦、余弦曲线. 3.理解y＝sin x与y＝cos x图象之间的联系. 通过利用定义和“五点法”作y＝sin x与y＝cos x的图象，重点提升学生的数学抽象、逻辑推理和直观想象素养.

新知探究 将塑料瓶底部扎一个小孔做成一个漏斗，再挂在架子上，就做成了一个简易单摆(如图(1)所示).在漏斗下方放一块纸板，板的中间画一条直线作为坐标系的横轴.把漏斗灌上细沙并拉离平衡位置，放手使它摆动，同时匀速拉动纸板.这样就可在纸板上得到一条曲线，它就是简谐运动的图象.物理中把简谐运动的图象叫做“正弦曲线”或“余弦曲线”.它表示了漏斗对平衡位置的位移s(纵坐标)随时间t(横坐标)变化的情况.图(2)就是某个简谐运动的图象. 问题 1.通过上述实验，你对正弦函数、余弦函数图象的直观印象是怎样的？ 2.你能比较精确地画出y＝sin x在[0，2π]上的图象吗？ 3.以上方法作图虽然精确，但太麻烦，有没有快捷画y＝sin x，x∈[0，2π]图象的方法？你认为图象上哪些点是关键点？ 提示 1.正、余弦函数的图象是“波浪起伏”的连续光滑曲线. 2.能，利用特殊角的三角函数值. 3.五点作图法 y＝sin x的五点：(0，0)，π2，1，(π，0)，

3π

2，－1，(2π，0)；

y＝cos x的五点：(0，1)，π2，0，(π，－1)，

3π

2，0，(2π，1).

1.正弦函数、余弦函数的图象 两者的图象可以通过左右平移得到 函数 y＝sin x y＝cos x

图象 图象画法 “五点法” “五点法” 关键五点 (0，0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0) (0，1)，(π2，0)，(π，－1)，(3π2，0)，(2π，1) 2.(1)正弦函数的图象叫做正弦曲线，是一条“波浪起伏”的连续光滑曲线. (2)余弦函数y＝cos x，x∈R的图象叫做余弦曲线，它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线. 3.正弦函数、余弦函数的值域 (1)y＝sin x，x∈R的值域为[－1，1]； (2)y＝cos x，x∈R的值域为[－1，1]. 拓展深化 [微判断] 1.正弦函数y＝sin x的图象向左右和上下无限伸展.(×) 提示 正弦函数y＝sin x的图象向左右无限伸展，但上下限定在直线y＝1和y＝－1之间. 2.函数y＝sin x与y＝sin(－x)的图象完全相同.(×) 提示 二者图象不同，而是关于x轴对称.