buffon投针
- 格式:doc
- 大小:28.50 KB
- 文档页数:2

Buffon 掷针实验的计算机模拟实验的设计与实现收稿日期:2018-12-05基金项目:长沙理工大学大学生研究性学习与创新性实验项目(1203058);长沙理工大学教研教改项目(CNJG201808)作者简介:周浙泉,王志宇,张棣妍(女),隆超怡(女),长沙理工大学信息与计算科学专业2014级学生;万勇(1963-),硕士研究生,教授,研究方向:几何分析与偏微分方程。
一、研究背景18世纪,蒲丰(Buffon )提出Buffon 投针问题:(1)取一张白纸,在上面画上许多条间距为a 的平行线。
(2)取一根长度为l (l ≤a/2)的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m 。
(3)计算针与直线相交的概率。
蒲丰证明了这个概率是:p=2l πa。
因为它与π有关,人们想到利用投针实验来估计圆周率的值。
历史上,有不少人做过蒲丰掷针实验:这个问题十分有趣,只是人工实验往往耗时、耗力,而用计算机模拟实验,却能迅速获得结果。
自从20世纪90年代美国率先开始数学实验以来,数学实验改变了人们传统的数学思维方式,人们发现数学是可以借助计算机去探索和发现的。
近十年来,国内外已有不少的数学实验教材和一些好的数学实验范例,但是这需要一定的计算机编程能力,如math-ematica 编程、matlab 编程等,才能实现人机对话,因此数学实验只能在具有一定数学知识和较高计算机编程能力的特定人群中使用,不能“飞入寻常百姓家”。
二、系统的设计本系统研发工具为Java 语言。
Java 是一门面向对象编程语言,不仅吸收了C++语言的各种优点,还作为静态面向对象编程语言的代表,极好地实现了面向对象理论,允许程序员以优雅的思维方式进行复杂的编程。
Java 看起来设计得很像C++,但是能够自动处理对象的引用和间接引用,实现自动的无用单元收集,使用户不必为存储管理问题烦恼,能将更多的时间和精力花在研发上。
Java 是一个面向对象的语言。




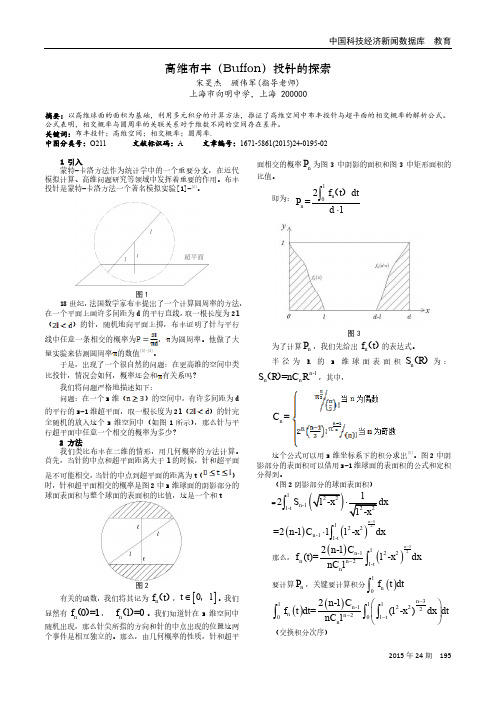
蒲丰投针问题的推广及其应用
张德然
【期刊名称】《阜阳师范学院学报:自然科学版》
【年(卷),期】1997(000)001
【摘要】本文从投针到投平面图形对蒲丰投针问题给出了一些推广,并指出了其概率规律及其在探矿,近拟计算中的应用。
【总页数】3页(P17-19)
【作者】张德然
【作者单位】无
【正文语种】中文
【中图分类】O211.2
【相关文献】
1.利用蒲丰(Buffon)投针问题在Excel中模拟π值 [J], 宗凤喜;李如兵
2.改进的蒲丰投针问题探究 [J], 代永嘉
3.蒲丰(Buffon)投针问题的一些推广 [J], 马丽;韩新方;杨小雪
4.基于蒲丰投针问题研究数学的“统一美” [J], 宋浩强
5.以皓骏设计“蒲丰投针”问题的积件及教学应用 [J], 谭势威;邹灵杰;黄永幸因版权原因,仅展示原文概要,查看原文内容请购买。
数学学习真正悲哀的就是,记住了某个神奇而伟大的定理,看懂了其最严密的推导过程,但却始终没能直观地去理解它。
虽然严密的推导是必要的,直观理解往往是不准确的,但如果能悟出一个让定理一瞬间变得很显然的解释,这不但是一件很酷的事,而且对定理更透彻的理解和更熟练的运用也很有帮助。
我惊奇地发现,国内的每一本高数课本上都严格地讲解了微积分基本定理的证明,但几乎没有任何一个课本上讲过积分等于函数下方的图形面积究竟是为什么。
事实上,这几乎是显然的,但还是有不少人学完微积分后仍然没有意识到。
每当谈到这个问题时,我更愿意首先提出一个非常有启发性的事实——圆的周长是2·pi·r,圆的面积就是pi·r^2,后者的导数正好就是前者。
这个现象是很容易理解的,因为圆的半径每增加一点,面积增加的就是周长那么一圈,换句话说面积的变化就等于周长。
类似地,如果你能找到一个函数g(x),它的导数正好就是f(x),那么当x每增加一点,g(x)就增加了一条小竖线段,显然g(x)就应当是f(x)下方的面积。
看清了这一点之后,我们才能欣赏到微积分基本定理真正牛B的地方。
原先大家都是用分割求极限的办法来求函数下方的面积,但Leibniz却把面积看作一个可变的整体,用一种办法“一下子”就把它求了出来。
有趣的是,这种现在看来如此自然的神奇办法,一千多年来居然没有任何人想到。
数学中有很多直观上看很不可思议的东西。
比如,神秘的常数pi就经常出现在一些貌似和它毫无关系的地方,其中最经典的例子莫过于Buffon投针实验。
Buffon投针实验是说,假设地板上画着一组间距为1的平行线。
把一根长度为1的针扔到地上,则这根针与地板上的平行线相交的概率为2/pi。
很多概率论课本上都会用微积分计算可行范围的方法求解Buffon投针问题,计算过程显得相当麻烦。
我一直觉得,这个问题一定有一个异常直观、一目了然的解释,不过我还从来没见到过,自己也没有想到过。
今天,我偶然看到了这个网页,猛地一下恍然大悟。
期望值的一个最引人注目的性质就是,E(A+B)=E(A)+E(B),不管A和B是不是独立的。
想象一根长度为L的铁丝,不管它被弯成了什么形状,扔到地上后它与地板上的平行线的交点个数的期望值都是一样的,并且这个值是和L成正比的。
这是因为,我们可以把一根弯铁丝看作很多很多小的直线段构成;而每个充分小的直线段与平行线交点个数的期望都是相同的,那么由期望值的线性关系,整个弯铁丝与平行线交点
数的期望就是c·L,其中c是某个固定的系数。
为了求出这个系数是多少,我们只需要考虑一些特殊的情况。
注意到,把一根长度为pi的铁丝弯成一个直径为1的圆,则把它扔到地上之后,它与这组平行线总有两个交点。
这就是说,pi的c倍就等于2,即c等于2/pi。
自然,一根单位长度的针与平行线的交点个数的期望值就是2/pi;而由于这根针与平行线要么没有交点,要么就只有一个交点,因此这个数值就相当于是针与平行线相交的概率了。