下载文档原格式
教材提到了“投针实验”求圆周率的方法。
1777年，法国数学家蒲丰取一根针，量出它的长度，然后在纸上画上一组间距相等的平行线，这根针的长度是这些平行线的距离是的一半。
把这根针随机地往画满了平行线的纸面上投去。
小针有的与直线相交，有的落在两条平行直线之间，不与直线相交。
这次实验共投针2212次，与直线相交的有704次，2212÷704≈3.142。
得数竟然是π的近似值。
这就是著名的蒲丰投针问题。
后来他把这个试验写进了他的论文《或然性算术尝试》中。
蒲丰证明了针与任意平行线相交的概率为p= 2l/πd 。
这个公式中l为小针的长，d为平行线的间距。
由这个公式，可以用概率方法得到圆周率的近似值。
当实验中投的次数相当多时，就可以得到π的更精确的值。
蒲丰实验的重要性并非仅仅是为了求得比其它方法更精确的π值。
而在于它是第一个用几何形式表达概率问题的例子。
计算π的这一方法，不但因其新颖，奇妙而让人叫绝，而且它开创了使用随机数处理确定性数学问题的先河，是用偶然性方法去解决确定性计算的前导。
找一根粗细均匀，长度为 d 的细针，并在一张白纸上画上一组间距为l 的平行线（方便起见，常取l = d/2），然后一次又一次地将小针任意投掷在白纸上。
这样反复地投多次，数数针与任意平行线相交的次数，布丰（Comte de Buffon）设计出他的著名的投针问题（needleproblem）。
依靠它，可以用概率方法得到π的近似值。
假定在水平面上画上许多距离为a的平行线，并且，假定把一根长为l＜a的同质均匀的针随意地掷在此平面上。
布丰证明：该针与此平面上的平行线之一相交的概率为：p=2l/(api) 把这一试验重复进行多次，并记下成功的次数，从而得到P的一个经验值，然后用上述公式计算出π的近似值，用这种方法得到的最好结果是意大利人拉泽里尼（Lazzeri ni）于1901年给出的。
布丰投针实验公元1777年的一天，法国科学家D•布丰(D.Buffon1707～1788)的家里宾客满堂，原来他们是应主人的邀请前来观看一次奇特试验的。
试验开始，但见年已古稀的布丰先生兴致勃勃地拿出一张纸来，纸上预先画好了一条条等距离的平行线。
接着他又抓出一大把原先准备好的小针，这些小针的长度都是平行线间距离的一半。
然后布丰先生宣布：“请诸位把这些小针一根一根往纸上扔吧!不过，请大家务必把扔下的针是否与纸上的平行线相交告诉我。
”客人们不知布丰先生要玩什么把戏，只好客随主意，一个个加入了试验的行列。
一把小针扔完了，把它捡起来又扔，而布丰先生本人则不停地在一旁数着、记着，如此这般地忙碌了将近一个钟头。
最后，布丰先生高声宣布：“先生们，我这里记录了诸位刚才的投针结果，共投针2212次，其中与平行线相交的704次。
总数2212与相交数704的比值为3.142。
”说到这里，布丰先生故意停了停，并对大家报以神秘的一笑，接着有意提高声调说：“先生们，这就是圆周率π的近似值!”众客哗然，一时疑议纷纷，大家全部感到莫名期妙：“圆周率π?这可是与圆半点也不沾边的呀!”布丰先生似乎猜透了大家的心思，得意洋洋地解释道：“诸位，这里用的是概率的原理，如果大家有耐心的话，再增加投针的次数，还能得到π的更精确的近似值。
不过，要想弄清其间的道理，只好请大家去看敝人的新作了。
”随着布丰先生扬了扬自己手上的一本《或然算术试验》的书。
π在这种纷纭杂乱的场合出现，实在是出乎人们的意料，然而它却是千真万确的事实。
由于投针试验的问题，是布丰先生最先提出的，所以数学史上就称它为布丰问题，布丰得出的一般结果是：如果纸上两平行线间相距为d，小针长为l，投针的次数为n，所以投的针当中与平行线相交的次数的m，那么当n相当大时有：π≈(2ln)/(dm)在上面故事中，针长l恰等于平行线间距离d的一半，所以代入上面公式简化得：π≈n/m值得一提的是，后来有不少人步布丰先生的后尘，用同样的方法来计算π值。
蒲丰投针实验原理
蒲丰投针实验是一种检测泥沙粒径分布的实验方法，它是利用悬浮在水中的粒度分布模拟藉由空气流抛掷及落入平板上的控制情形来模拟河流中悬浮颗粒的粒径分布，从而进行检测的。
该实验流程是：将检测的粒料悬浮于水中，利用抛掷及落入平板上的控制条件来模拟河流中悬浮颗粒的粒径分布，然后借助投针实验来观测平面上粒料的分布情况。
最后，根据获得的结果计算出每种粒径的百分率，从而可以得出泥沙粒径分布情况。
投针实验计算圆周率的数学分析王向东投针实验计算圆周率的数学证明方法，初中一般是采取假设针弯成直径等于平行线距离的方法巧妙证明。
这个方法是基于不管针弯成什么形状，针上的每一个部位与平行线相交的概率相同，但这是感观上的认识，要把其中原因解释清楚不是很容易。
笔者从纯数学的角度来推导这个公式。
一、投针问题的由来1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的蒲丰投针问题。
这一方法的步骤是：1) 取一张白纸，在上面画上许多条间距为d 的平行线。
2) 取一根长度为()l l d <的针，随机地向画有平行直线的纸上掷n 次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为d 的平行线，将一根长度为()l l d <的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。
”布丰本人证明了，这个概率是：2lp d π=，π为圆周率。
二、投针实验的数学证明投针这个动作是由两个事件构成的。
事件1：针投下后与平行线构成一定的夹角。
我们来分析一下针投下后与平行线之间的成某一特定夹角时的概率。
设针投下后与平行线之间的夹角为θ，则θ在0与π之间。
针与平行线之间的夹角在θ到θ+θ∆之间的概率为1p θπ∆=，当0θ∆→时，可看作针投下后与平行线之间成某一特定夹角为θ的概率。
事件2：针投下后会在平行线垂直的方向形成一个投影，针与平行线相交等于它的垂直投影与平行线相交。
这个投影的长度'l 在0到l 之间。
此时针在水平方向的投影为'sin()l l θ=。
再分析'l 与平行线相交的概率。
等于我们将问题转化成长度为'l 的针，并且只允许它处在与平行线垂直的方向上，这时它与平行线相交的概率显然为：2'sin()l l p d d θ==因为每一次投掷都是由上述两个事件组成的，因而对于针与平行线之间的夹角在θ到θ+θ∆之间时，针与平行线相交的概率()p θ为这两个事件概率的乘积，即：12sin()().l p p p d θθθπ∆== 因为针与平行线之间构成的夹角在0－π之间每个角度的机会都是均等的，因此针与平行线相交的概率相当于针落在每个θ附近θ∆范围内，当0θ∆→时与平行线相交的所有概率之和。
6·2 投针试验1.投针试验活动步骤：①分组，两人一组。
②取一张白纸，在上面画一组平行线，它们之间的距离约为2cm，另外备一根1cm长的针，在纸的下面垫一层柔软的东西，便针落在纸面上时不会弹跳。
③每组至少完成100次试验，分别记录下其中相交和不相交的次数。
④统计全班试验数据，估计针与平行线相交的概率。
2.求等可能事件发生的概率常有下列两种法：画树状图法、列表法。
在求可能事件的概率用列表法和树状图法时，应注意各种情况出现的可能性务必相同。
3.注意的问题：（1）列表法和树状图法适用于各种情况出现的总次数不是很大时求概率的问题；（2）在求可能事件的概率用列表法和树状图法时，应注意各种情况出现的可能性务必相同；（3）在列表或画树状图求概率的过程中，各种情况的可能性不能重复，也不能遗漏。
例1.中考前夕，某校为了了解初三年级480名学生的数学学习情况，特组织了一次检测。
教师随机抽取了一部分学生的检测成绩进行统计分析，绘制成下表：注：72分（含72分）以上为“及格”；96分（含96分）以上为“优秀”；36分（不含36分）以下为“后进”，全距是“最高分”与“最低分”之差。
（1）仔细观察上表，填出表中空格处的相应数据；（2）估计这480名学生本次检测成绩的中位数落在哪个分数段内；（3）根据表中相关统计量及相应数据，结合你所学的统计知识，选择两个方面对这次检测的总体情况作出合理分析。
解：（1）样本容量：50。
优秀率：3400。
频数：4。
频率：0.18。
（2）中位数落在85～95.5这一分数段内（3）略。
评分说明：只要选择了两个方面作答，分析合理 叙述准确，用语精炼，体现用样本估计总体的思想.例2.你喜欢玩游戏吗？现请你玩一个转盘游戏。
如图所示的两个转盘中指针落在每一个数字上的机会均等，现同时自由转动甲乙两个转盘，转盘停止后，指针各指向一个数字，用所指的两个数字作乘积。
请你：⑴列举（用列表或画树状图）所有可能得到的数字之积⑵求出数字之积为奇数的概率。
实验说明1：蒲丰投针一、 实验目的1、 运用基本采样技术计算积分；2、 体会用随机模拟方法解决实际问题。
二、 问题描述在历史上人们对π的计算非常感兴趣性，发明了许多求π的近似值的方法。
1777年法国科学家蒲丰（Buffon ）提出并解决了如下的投针问题来近似求解π。
蒲丰投针问题如图1所示。
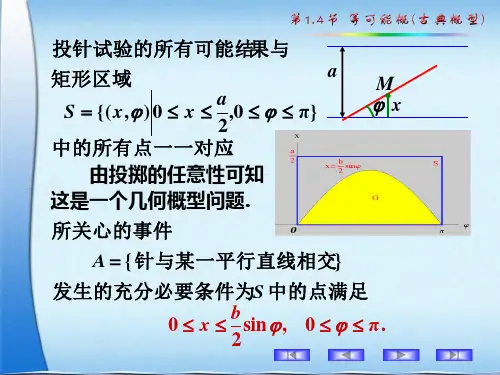
桌面上画有间隔为a (a >0) 的一些平行线，向平面任意投一枚长为l (l <a )的针，可以通过求针与任一平行线相交的概率，进而求得π的近似值。
用X 表示针的中点与最近一条平行线的距离，Y 表示针与此直线间的夹角。
如果sin 2X l Y <，或sin 2l X Y <时，针与一条直线相交。
图1：蒲丰投针示意图由于向桌面投针是随机的，所以可以用二维随机向量(X ,Y )来确定针在桌面上位置。
并且X 在0,2a ⎛⎞⎜⎜⎜⎝上服从均匀分布， Y 在0,2π⎛⎞⎟⎜⎟⎜⎟⎜⎝⎠上服从均匀分布, X 与Y 相互独立。
由此可以写出的联合概率密度函数为： ()40,0,220a x y f x y a ππ⎧⎪⎪<<<<⎪=⎨⎪⎪⎪⎩其他。
用随机事件A 针与平行线相交，则事件A 发生的概率为{}()sin 2200sin 242sin ,2l y l x y l l A X Y f x y dxdy dxdy a aπππ<⎧⎫⎪⎪=<===⎨⎬⎪⎪⎪⎪⎩⎭∫∫∫∫P P 。
如果{}A P 已知，则有该概率得到{}2l a A π=P 。
当蒲丰的实验中，通过投针N 次，其中针与平行线相交n 次，用频率n N 作为{}A P 的估计值，于是得到2Nl anπ≈。
三、 实验内容1、上述概率{}A P 为积分计算，可用Monte Carlo 积分近似。
通过从分布(),f x y 中产生随机数，近似积分{}A P ，从而计算π；2、当样本数N （N =50、100、1000、10000、50000）时，每个N 重复10次实验。
一、问题的提出
在人类数学文化史中，对圆周率π精确值的追求吸引了许多学者的研究兴趣。
在众多的圆周率计算方法中，最为奇妙的是法国物理学家布丰（Boffon）在1777年提出的“投针实验”。
与传统的“割圆术”等几何计算方法不同的是，“投针实验”是利用概率统计的方法计算圆周率的值，进而为圆周率计算开辟了新的研究途径，也使其成为概率论中很有影响力的一个实验。
本节我们将借助于MATLAB仿真软件，对“投针实验”进行系统仿真，以此来研究类比的系统建模方法和离散事件系统仿真。
二、系统建模
“投针实验”的具体做法是：在一个水平面上画上一些平行线，使它们相邻两条直线之间的距离都为a；然后把一枚长为l(0<l<a)的均匀钢针随意抛到这一平面上。
投针的结果将会有两种，一种是针与这组平行线中的一条直线相交，一种是不相交。
设n为投针总次数，k为相交次数，如果投针次数足够多，就会发
现公式2ln
ak
计算出来的值就是圆周率π。
当然计算精度与投针次数有关，一般情
况下投针次数要到成千上万次，才能有较好的计算精度。
有兴趣的读者可以耐心地做一下这个实验。
90
)
相交
为了能够快速的得到实验结果，我们可以通过编写计算机程序来模拟这个实验，即进行系统仿真。
所谓的系统仿真是指以计算机为工具，对具有不确定性因素的、可模型化的系统的一种研究方法。
建立能够反映实验情况的数学模型是系统仿真的基础。
系统建模中需解决两个问题，一个是如何模拟钢针的投掷结果，
另一个是如何判断钢针与平行线的位置关系。
这里，设O 为钢针中点，y 为O 点与最近平行线之间的距离，θ为钢针与平行线之间的夹角（0180θ≤<）。
首先，由于人的投掷动作是随机的，钢针落下后的具体位置也是随机的，因此可用按照均匀分布的两个随机变量y 和θ来模拟钢针投掷结果。
其次，人工实验时可以用眼睛直接判断出钢针是否与平行线相交，而计算机仿真实验则需要用数学的方法来判别。
如下图所示，如果y 、l 和θ满足关系式
1sin 2
y l θ≤，那么钢针就与平行线相交，否则反之，进而可以判断钢针与平行线的位置关系。
三、 基于MATLAB/SIMULNIK 的仿真实验
在系统模型基础上，我们可以绘制出程序的流程图如下所示。
根据流程图，在MATLAB 环境下可编写程序完成计算机系统仿真实验，在这
里我们设定平行线之间的距离为40cm a =，钢针长为30cm L =，计算精度0.00001pi επ=-=，这些参数可以根据实际情况做以修改，下面是仿真程序：
%投针实验：计算机模拟投针实验，计算圆周率%
clear
format long
a=40,L=30;n=0;k=0;pii=0; %主要参数值
while(abs(pii-pi)> %设置计算精度
n=n+1;
y=1/2*a*rand(1); %生成[0,a)区间的随机数 q=pi*rand(1); %生成[0，180)区间的随机数 if(y<1/2*L*sin(q)) %判断钢针与平行线是否相交 k=k+1;
pii=2*L*n/(a*k); %计算圆周率
end
disp('此次实验情况:')
disp('投掷次数:')
disp(n) %显示投掷次数
disp('相交次数:')
disp(k) %显示钢针与平行线相交次数 disp('实验结果:pi=')
disp(pii) %显示计算出的圆周率值 end
通过程序中的注释可以很好的理解程序内容。
程序运行时，将显示出每次的“投针实验”情况，即显示当前总投掷次数、钢针与平行线相交次数以及由此计算出来的圆周率值。
当满足所设置的精度要求后，程序停止运行,此时显示出当钢针投掷 276427次后，所计算出来的圆周率值满足精度要求，此时钢针与平行
线相交131984次，圆周率计算结果为。
当然，由于“投掷动作”具有随机性，因此每次“投针实验”的仿真结果不一定相同。
为使计算结果更趋近于π，可以减小误差ε的取值来提高计算精度，当然仿真时间也会随之变长。
这里对投针实验的基本原理做一简单解释。
首先，将一根钢丝弯成一个圆圈，使其直径恰好等于平行线间的距离a 。
可以想象得出，对于这样的圆圈来说，投掷结果不外乎有两种：一种是与一条平行线相交，一种是与相邻两根平行线相切，这两种情况都将导致圆圈和平行线有两个交点。
因此，如果圆圈扔下的次数为n ，那么相交的交点数必为2n 。
然后，将圆圈拉直变成一条长为a π的钢针。
显然，这样的钢针扔下时与平行线相交的情形要比圆圈复杂得多，可能没有交点，有1个交点，2个交点，3个交点，4个交点。
由于圆圈和拉直后的钢针的长度相同，根据机会均等的原理，当它们投掷次数足够多时，两者与平行线组交点的总数将是一样的。
换句话说，当长度为a π的钢针扔下无穷多次后，与平行线相交的交点总数也为2n 。
最后，讨论钢针长为l 的情形。
由于钢针与平行线相交的交点总数k 与钢针长度l 成正比，则存在下列比例关系式:2:k l n a π=，进而可求得2ln ak
π=。
四、结论
从本质上看，上述投针实验具有朴素的离散事件系统仿真思想。
如果按照布丰的做法，进行成千上万次的投针实验和手工计算，势必要消耗大量的人力、物力和财力。
而通过类比的方法，对实验进行系统建模，在此基础上使用计算机进行系统仿真，以此来解决“投针问题”将变得非常简单。
从中我们可得出以下结论：
首先，有意识地运用类比方法将有助于掌握复杂事物的内在规律，显著提升数学建模能力。
数学建模的过程蕴含着许多重要的数学思想和方法，其中类比方法是最重要也是最有效的一种。
类比建模的过程可表述为，根据已掌握的对客观事物的经验与认识，通过抽象分析运用数学语言、数学符号、数学公式等数学概念来表达这些量，从多种复杂因素中抽取主要因素，忽略次要因素，抓住事物的
本质特征，运用一系列等式或不等式来表达各个量之间的关系，建立起研究对象的数学模型。
其次，在建好的数学模型基础上，通过计算机进行系统仿真可对研究对象进行快速有效的模拟。
20世纪40年代以后，随着电子计算机的出现和发展，人们可以选择适当的软件和编程方法，使用计算机来模拟仿真一些实验和计算。
计算机具有计算速度快和存储容量大的优点，采用系统仿真技术可以代替许多实际上非常庞大而复杂的实验，并将实验结果快速的进行运算处理和结果分析，上述“投针实验”已经证明了这一点。
