投针试验PPT课件

6.2投针试验主备人：周利敏一、本课程的目标是什么？1、经历实验、统计等活动过程，在活动中进一步发展学生合作交流的意识和能力。

2、能用实验的方法估计一些复杂的随机事件发生的概率。

3、能力训练要求：通过活动操作，培养学生解决问题的能力。

4、情感与价值观：经历将一些复杂数学问题，用实验的方法解决。

让学生感到从事着一项极具探秘色彩的游戏活动。

让数学教育真正走进学生的世界，为他们所关注、喜爱、认同和向往。

二、本课程的教学重、难点是什么？重点：掌握实验方法估计一些复杂的随机事件发生的概率。

难点：对复杂事件发生的概率的体验教学方法。

三、核心问题是什么？1、经历实验、统计等活动过程，在活动中进一步发展学生合作交流的意识和能力。

2、能用实验的方法估计一些复杂的随机事件发生的概率。

3、让学生通过亲身的试验、统计过程获得用试验方法估计复杂事件发生的概率。

4、让学生参与活动,在合作交流中,发现惊奇的结论,感受数学的魅力。

四、教学设计策略及评价方法是什么？活动一：1.提出问题：平面上画着一些平行线，相邻的两条平行线之间的距离都为2cm，向此平面任投一长度为lcm的针，该针可能与其中某一条平行线相交，也可能与它们都不相交。

相交和不相交的可能性相同吗？你能通过列表或画树状图求出该针与平行线相交的概率吗？2、活动目的：利用当“试验次数较大时，试验频率稳定于某一试验概率”并据此估计针与平行线相交的概率。

3、活动用具：（1）桌子，（2）铁针若干枚，长度为lcm，粗细一致，﹙3﹚表格。

注意：每位同学的针都一样。

4、活动方式：小组合作交流，全班研讨。

5、活动步骤：（1）将学生分成两人一组，（2）利用一张大白纸，在纸上画出等距离2ｃｍ的8条平行线（线条要细）。

（3）准备若干枚长度为1ｃｍ的针（4）要求学生从一定高度随意抛针，保证投针的随意性；组内同学分工如下：一位投针，一位记录。

注意问题：在试验中有时针与线是否相交较难判断，采取的方法：（1）忽略这次试验；（2）认为相交、不相交各计半次，等等。

一、 问题的提出在人类数学文化史中，对圆周率π精确值的追求吸引了许多学者的研究兴趣。

在众多的圆周率计算方法中，最为奇妙的是法国物理学家布丰（Boffon ）在1777年提出的“投针实验”。

与传统的“割圆术”等几何计算方法不同的是，“投针实验”是利用概率统计的方法计算圆周率的值，进而为圆周率计算开辟了新的研究途径，也使其成为概率论中很有影响力的一个实验。

本节我们将借助于MATLAB 仿真软件，对“投针实验”进行系统仿真，以此来研究类比的系统建模方法和离散事件系统仿真。

二、 系统建模“投针实验”的具体做法是：在一个水平面上画上一些平行线，使它们相邻两条直线之间的距离都为a ；然后把一枚长为l (0<l <a )的均匀钢针随意抛到这一平面上。

投针的结果将会有两种，一种是针与这组平行线中的一条直线相交，一种是不相交。

设n 为投针总次数，k 为相交次数，如果投针次数足够多，就会发现公式2ln ak计算出来的值就是圆周率π。

当然计算精度与投针次数有关，一般情况下投针次数要到成千上万次，才能有较好的计算精度。

有兴趣的读者可以耐心地做一下这个实验。

为了能够快速的得到实验结果，我们可以通过编写计算机程序来模拟这个实验，即进行系统仿真。

所谓的系统仿真是指以计算机为工具，对具有不确定性因素的、可模型化的系统的一种研究方法。

建立能够反映实验情况的数学模型是系统仿真的基础。

系统建模中需解决两个问题，一个是如何模拟钢针的投掷结果，另一个是如何判断钢针与平行线的位置关系。

这里，设O 为钢针中点，y 为O 点与最近平行线之间的距离，θ为钢针与平行线之间的夹角（0180θ≤< ）。

首先，由于人的投掷动作是随机的，钢针落下后的具体位置也是随机的，因此可用按照均匀分布的两个随机变量y 和θ来模拟钢针投掷结果。

其次，人工实验时可以用眼睛直接判断出钢针是否与平行线相交，而计算机仿真实验则需要用数学的方法来判别。

如下图所示，如果y 、l 和θ满足关系式1sin 2y l θ≤，那么钢针就与平行线相交，否则反之，进而可以判断钢针与平行线的位置关系。

1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的蒲丰投针问题。

投针步骤这一方法的步骤是：1) 取一张白纸，在上面画上许多条间距为d的平行线。

2) 取一根长度为l（l<d）的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为d的平行线，将一根长度为l（l<d）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。

”布丰本人证明了，这个概率是p=2l/(πd) π为圆周率利用这个公式可以用概率的方法得到圆周率的近似值。

下面是一些资料实验者年代投掷次数相交次数圆周率估计值沃尔夫1850 5000 2531 3.1596史密斯1855 3204 1219 3.1554德摩根1680 600 383 3.137福克斯1884 1030 489 3.1595拉泽里尼1901 3408 1808 3.1415929赖纳1925 2520 859 3.1795布丰投针实验是第一个用几何形式表达概率问题的例子，他首次使用随机实验处理确定性数学问题，为概率论的发展起到一定的推动作用。

像投针实验一样，用通过概率实验所求的概率来估计我们感兴趣的一个量，这样的方法称为蒙特卡罗方法（Monte Carlo method）。

蒙特卡罗方法是在第二次世界大战期间随着计算机的诞生而兴起和发展起来的。

这种方法在应用物理、原子能、固体物理、化学、生态学、社会学以及经济行为等领域中得到广泛利用。

法国数学家布丰（1707-1788）最早设计了投针试验。

并于1777年给出了针与平行线相交的概率的计算公式P=2L/πd(其中L是针的长度，d是平行线间的距离，π是圆周率)。

由于它与π有关，于是人们想到利用投针试验来估计圆周率的值。

此外，随便说出3个正数，以这3个正数为边长可以围成一个钝角三角形的概率P也与π有关，这个概率为(π-2)/4,证明如下：设这三个正数为x，y，z，不妨设x≤y≤z，对于每一个确定的z，则必须满足x+y>z，x&sup2;+y&sup2;﹤z&sup2;，容易证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件，用线性规划可知满足题设的可行域为直线x+y=z与圆x&sup2;+y&sup2;=z&sup2;围成的弓形，总的可行域为一个边长为z的正方形，则可以围成一个钝角三角形的概率P=S弓形/S正方形=(πz&sup2;/4-z&sup2;/2)/z&sup2;=(π-2)/4.因为对于每一个z，这个概率都为(π-2)/4，因此对于任意的正数x，y，z，有P=(π-2)/4，命题得证。

一、问题的提出在人类数学文化史中，对圆周率π精确值的追求吸引了许多学者的研究兴趣。

在众多的圆周率计算方法中，最为奇妙的是法国物理学家布丰（Boffon）在1777年提出的“投针实验”。

与传统的“割圆术”等几何计算方法不同的是，“投针实验”是利用概率统计的方法计算圆周率的值，进而为圆周率计算开辟了新的研究途径，也使其成为概率论中很有影响力的一个实验。

本节我们将借助于MATLAB仿真软件，对“投针实验”进行系统仿真，以此来研究类比的系统建模方法和离散事件系统仿真。

二、系统建模“投针实验”的具体做法是：在一个水平面上画上一些平行线，使它们相邻两条直线之间的距离都为a；然后把一枚长为l(0<l<a)的均匀钢针随意抛到这一平面上。

投针的结果将会有两种，一种是针与这组平行线中的一条直线相交，一种是不相交。

设n为投针总次数，k为相交次数，如果投针次数足够多，就会发现公式2lnak计算出来的值就是圆周率π。

当然计算精度与投针次数有关，一般情况下投针次数要到成千上万次，才能有较好的计算精度。

有兴趣的读者可以耐心地做一下这个实验。

90)相交为了能够快速的得到实验结果，我们可以通过编写计算机程序来模拟这个实验，即进行系统仿真。

所谓的系统仿真是指以计算机为工具，对具有不确定性因素的、可模型化的系统的一种研究方法。

建立能够反映实验情况的数学模型是系统仿真的基础。

系统建模中需解决两个问题，一个是如何模拟钢针的投掷结果，另一个是如何判断钢针与平行线的位置关系。

这里，设O 为钢针中点，y 为O 点与最近平行线之间的距离，θ为钢针与平行线之间的夹角（0180θ≤<）。

首先，由于人的投掷动作是随机的，钢针落下后的具体位置也是随机的，因此可用按照均匀分布的两个随机变量y 和θ来模拟钢针投掷结果。

其次，人工实验时可以用眼睛直接判断出钢针是否与平行线相交，而计算机仿真实验则需要用数学的方法来判别。

如下图所示，如果y 、l 和θ满足关系式1sin 2y l θ≤，那么钢针就与平行线相交，否则反之，进而可以判断钢针与平行线的位置关系。

布丰投针实验详解1777年，法国数学家布丰（D，Buffon，1707年-1788年）提出了随机投针法并通过投针实验计算出了圆周率π的值，与刘徽的“割圆术”不同的是，随机投针法是利用概率统计的方法来计算圆周率π的值，开辟了计算圆周率的新途径，因此，“布丰投针实验”成为概率论中很有影响力的一个实验。

程序运行时，计算机上将显示出每次“投针实验”的具体情况，即显示当前总投掷的次数、钢针与平行线相交的次数以及由此计算出来的圆周率的值，当满足所设置的精度要求后，程序就停止运行，当钢针投掷276427次后，所计算出来的圆周率值满足精度要求，此时钢针与平行线相交131984次，圆周率计算结果为3.14159670869196.当然，由于“投掷动作”具有随机性，因此每次“投针实验”的仿真结果不一定相同，为了使计算结果更趋近于π，可以减小误差，取更小的s的值来提高计算的精度，当然仿真实验的时间也会随之变长，值得说明的是，若将一根钢丝弯成一个圆圈，使其直径恰好等于平行线间的距离a，投掷的结果不外乎有两种：一种是与一条平行线相交，一种是与相邻两条平行线相切，这两种情况都将导致圆圈和平行线有两个交点，因此，如果圆圈扔下的次数为n，那么相交的交点数必为2n。

若将圆圈拉直变成一根长为πa的钢针，显然，这样的钢针被扔下时与平行线相交的情形要比弯成圆圈的情况复杂得多，可能没有交点，还可能有1个交点、2个交点、3个交点、4个交点，由于圆圈和拉直后的钢针的长度相同，根据机会均等的原理可知，当投掷的次数足够多时，两者与平行线组的交点的总数将是一样的，换句话说，当长度为πa的钢针被扔下无穷多次后，它与平行线相交的交点总数也为2n。

從本质上看，上述投针实验运用了离散事件系统仿真，如果按照布丰的做法，进行成千上万次的投针实验和手工计算，势必要消耗大量的人力、物力和财力，而通过运用类比的方法，对实验进行系统建模，在此基础上使用计算机进行系统仿真来解决问题，事情就会变得非常简单，我们只需要根据已掌握的经验与认识，通过对比分析1，运用数学语言、数学符号、数学公式、数学概念等来表达这些量，从多种复杂的因素中抽取主要因素，忽略次要因素，抓住事物的本质特征，运用一系列等式或不等式来表达各个量之间的关系，从而建立起研究对象的数学模型，这有助于掌握复杂事物的内在规律。

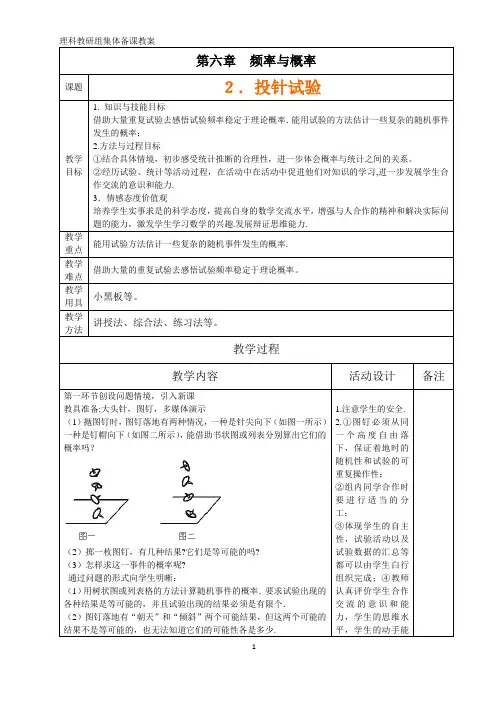
第六章频率与概率课题２．投针试验教学目标1. 知识与技能目标借助大量重复试验去感悟试验频率稳定于理论概率．能用试验的方法估计一些复杂的随机事件发生的概率；2.方法与过程目标①结合具体情境，初步感受统计推断的合理性，进一步体会概率与统计之间的关系。

②经历试验、统计等活动过程，在活动中在活动中促进他们对知识的学习,进一步发展学生合作交流的意识和能力.3．情感态度价值观培养学生实事求是的科学态度，提高自身的数学交流水平，增强与人合作的精神和解决实际问题的能力，激发学生学习数学的兴趣.发展辩证思维能力.教学重点能用试验方法估计一些复杂的随机事件发生的概率.教学难点借助大量的重复试验去感悟试验频率稳定于理论概率。

教学用具小黑板等。

教学方法讲授法、综合法、练习法等。

教学过程教学内容活动设计备注第一环节创设问题情境，引入新课教具准备:大头针，图钉，多媒体演示（1）抛图钉时，图钉落地有两种情况，一种是针尖向下（如图一所示）一种是钉帽向下（如图二所示），能借助书状图或列表分别算出它们的概率吗？（2）掷一枚图钉，有几种结果?它们是等可能的吗?（3）怎样求这一事件的概率呢?通过问题的形式向学生明晰：（1）用树状图或列表格的方法计算随机事件的概率．要求试验出现的各种结果是等可能的，并且试验出现的结果必须是有限个．（2）图钉落地有“朝天”和“倾斜”两个可能结果，但这两个可能的结果不是等可能的，也无法知道它们的可能性各是多少. 1.注意学生的安全.2.①图钉必须从同一个高度自由落下，保证着地时的随机性和试验的可重复操作性；②组内同学合作时要进行适当的分工；③体现学生的自主性，试验活动以及试验数据的汇总等都可以由学生白行组织完成；④教师认真评价学生合作交流的意识和能力，学生的思维水平，学生的动手能。

1 6．2 投针实验时间： 课时： 班级：初三（3）班教学目标教学目标：能用实验的方法估计一些复杂的随机事件发生的概率．能力目标：经历实验、统计等活动过程在活动中进一步发展学生的合作交流的意识和能力． 情感目标：1．激发学生实事求是的科学态度． 2．亲历实验，提高学生学习数学的兴趣．教学重点： 能用实验的方法估计一些复杂的随机事件发生的概率． 教学难点：借助大量重复实验去感悟实验频率稳定于理论概率． 教学方法：小组活动．教学媒体及准备：多媒体教学 多媒体课件 大头针，图钉 教学过程一．提出质疑，引入新课1、上节课我们介绍了用树状图或列表格的方法计算随机事件的概率．也就是计算一些事件的概率就可以在某个试验之前，算出某个结果的概率．但这些方法有一个前提条件，是什么?2、下面我们来看一个例子．比如掷一枚图钉，有几种结果?它们是等可能的吗? 有“朝天”和“倾斜”两个可能结果，但我觉得这两个可能的结果不是等可能的.3、能不能说“朝天”的概率是21，“倾斜”的概率也是21呢?4、再例如，掷一只墨水笔尖，也有“正”“反”两种可能，但出现的可能性相等吗? 很好．一个试验，虽然结果有有限个，但各个结果出现的可能性不相等，这时怎样求某一事件的概率呢? 二．讲授新课活动一：从一定高度落下的图钉，落地后可能钉尖着地，也可能钉帽着地．你估计哪种事件发生的概率大?活动目的：利用“当实验次数较大时，实验频率稳定于理论概率”来估计某一事件发生的概率．活动方式：小组合作交流，全班汇总实验数据，交流研讨． 活动工具：形状、大小完全相同的图钉．活动步骤：1．分组：每组5人．2．每组每人做20次实验，根据实验结果， 填写下表的表格：3．根据上表你认为哪种情况的频率较大?4．分别汇总本小组其中两人、三人、四人、五人的实验数据，相应得到实验40次、60次、80次、100次时钉帽着地的频率，填写下表，并绘制折线统计图．实验次数 20 40 60 80 100 钉帽着地的频数 钉帽着地的频率5．汇总全班各小组其一个组．两个组、三个组、四个组……的实验数据，相应得到实验100次、200次、300次、400次……时钉帽着地的频率，并绘制折线统计图． 6．由折线统计图，估计钉帽着地的概率．在数学的历史上，有一个较为著名的投针实验：平面上画着一些平行线，相邻的两条平行线之间的距离为a ，向此平面任投一长度为l(l<a)的针，该针可能与其中某一条平行线相交，也可能与它们都不相交．相交和不相交的可能性相同吗?你能通过列表或画树状图求出该针与平行线相交的概率吗? 活动二：平面上画着一些平行线，相邻的两条平行线之间的距离都是a ，向此平面任投一长度为l(l<a)的针，该针可能与其中某一条平行线相交，也可能与它们不相交，估计针与平行线相交的概率．活动目的：利用“当实验次数较大时，实验频率稳定于理论概率”，并据此估计针与平行线相交的概率．活动方式：小组交流，全班研讨的方法．活动工具：每组学生要在平面上画有相同距离“的一组平行线，并且有长度都为l 的针(l<a)．要求针必须粗细均匀． 活动步骤：1．分组，两人一组．2．取一张白纸，在上面画一组平行线．它们之间的距离为2厘米，另外准备一根1厘实验结果 钉尖着地钉帽着地频数 频率2 米长的针．在纸下面垫一层柔软的东西，使针落在纸面上时不会弹跳起来． 3．每组至少完成100次实验，分别记录下其中相交和不相交的次数． 4．统计全班的实验数据，估计针与平行线相交的概率[师]当针与直线相交时，必有其上的某1毫米处相交．而每1毫米最可能与直线相交的机会是相等的，它的次数应为全针与直线相交的最可能次数k 的101．如果针上某一段长n 毫米，那么这一段与直线最可能相交的次数应为10nk ，即最可能的相交次数和针的长度成正比．需要指出的是，这个最可能的相交次数只与针的长度成正比，而与针的形状无关．例如，我们将10毫米的针弯成两段，一段长x 毫米，另一段长为(10-x)毫米，那么这两段的最可能与直线相交的次数分别为10xk 和10)10(kx -.这样，全针的最可能相交次数仍为20)20(20kx xk -+＝k ，即这个最可能相交次数与针的形状无关．当然，将针的形状弯成某种形状后，有时可能在针的某儿处都和直线相交，这时应把每一个交点都记作相交一次． 现在将针弯曲成一个圆形．假定这时的针的粗细仍是均匀的，且圆的直径等于20毫米，那么每投一次圆环总能和直线相交于两点(正好和两条直线相切也记作两个交点)．投掷n 次，相交次数为2n 次．对于10毫米的针，它的最可能相交次数是k 次．由于圆环的长是π·20毫米，等于针长的2π倍，所以圆环相交次数应是针的最可能的相交次数的2π倍，即2n=2π·k ， 由此可得π=相交次数投掷总次数=k n三．课时小结这节课我们学会了用实验的方法估计一些复杂随机事件发生的概率，并亲自体验到了“当实验次数较大时，实验频率稳定于理论概率，并可据此估计某一事件发生的概率”．经历实验、统计等活动过程，在活动过程中，同学们都能积极参与到数学活动中去，合作意识和思维能力及思维水平得到了不同程度的提高，认识了蒙特卡罗方法，并用它来估计π的近似值． 四．课后作业1．习题6．32．继续做投针实验，估算π的值． Ⅴ．活动与探究随便说出3个正数，以这3个数为边长一定能围成一个三角形吗?一定能围成一个钝角三角形(其中最大边的平方大于另两边的平方和)吗?估计能围成一个钝角三角形的概率． [过程]本题仍是利用实验的方法估计随机事件发生的概率，选择该题材的原因是其概率与π有关，并与“读一读”中内容相呼应．具体操作时，可以几个学生组成合作小组，每人写一个数在纸上，然后同时公布各自的数进行判断．随便说出三个正数，以这三个正数为边不一定能组成一个三角形，如不能以1，3，5三个数为边长组成三角形；当然也不一定能组成一个钝角三角形；能围成一个钝角三角形的概率的估计值因人而异，因实验次数而异．事实上，不妨设所取三数为(a ，b ，c(0<a ≤b≤c)，若能构成钝角三角形，则a ，b ，c 应满足a+b>c ，a 2+b 2<c 2．即cb ca +>1，2222cb ca +<1． [结果]其理论概率为42-π.。

一、问题的提出在人类数学文化史中，对圆周率兀精确值的追求吸引了许多学者的研究兴趣。

在众多的圆周率计算方法中，最为奇妙的是法国物理学家布丰(Boffon)在1777年提出的“投针实验”。

与传统的“割圆术”等儿何计算方法不同的是，“投针实验”是利用概率统讣的方法讣算圆周率的值，进而为圆周率计算开辟了新的研究途径，也使其成为概率论中很有影响力的一个实验。

本节我们将借助于MATLAB仿真软件，对“投针实验”进行系统仿真，以此来研究类比的系统建模方法和离散事件系统仿真。

二、系统建模“投针实验”的具体做法是：在一个水平面上画上一些平行线，使它们相邻两条直线之间的距离都为然后把一枚长为；(0＜；＜a)的均匀钢针随意抛到这一平面上。

投针的结果将会有两种，一种是针与这组平行线中的一条直线相交，一种是不相交。

设力为投针总次数，&为相交次数，如果投针次数足够多，就会发现公式竺讣算出来的值就是圆周率兀。

当然汁算精度与投针次数有关，一般情ak况下投针次数要到成千上万次，才能有较好的计算精度。

有兴趣的读者可以耐心地做一下这个实验。

为了能够快速的得到实验结果，我们可以通过编写计算机程序来模拟这个实验，即进行系统仿真。

所谓的系统仿真是指以计算机为工具，对具有不确定性因素的、可模型化的系统的一种研究方法。

建立能够反映实验情况的数学模型是系统仿真的基础。

系统建模中需解决两个问题，一个是如何模拟钢针的投掷结果，另一个是如何判断钢针与平行线的位置关系。

这里，设0为钢针中点，y为0点与最近平行线之间的距离，&为钢针与平行线之间的夹角(0 S&V180 )。

首先，山于人的投掷动作是随机的，钢针落下后的具体位置也是随机的，因此可用按照均匀分布的两个随机变量y和&来模拟钢针投掷结果。

其次，人工实验时可以用眼睛直接判断出钢针是否与平行线相交，而计算机仿真实验则需要用数学的方法来判别。

如下图所示，如果八2和&满足关系式y<-/sin^,那么钢针就与平行线相交，否则反之，进而可以判断钢针与平行线2的位置关系。

第六章第2节投针试验教学目标1经历试验、统计等活动过程，在活动中进一步发展学生合作交流的意识和能力。

2.能用试验的方法估计一些复杂的随机事件发生的概率。

教学重点:能用试验方法估计一些复杂的随机事件发生的概率.教学难点:借助大量的重复试验去感悟试验频率稳定于理论概率.课前准备：牙签（用来替代针）、直尺、计算器、画有平行线的纸。

多媒体辅助。

教学方法：本节课基本上是一节活动课，因而要体现学生的自主性，试验活动以及试验数据的汇总等都可以由学生自行组织完成。

让学生真正体验到了“当实验次数较大时，实验频率稳定于理论概率，并可据此估计某一事件发生的概率”。

力图让学生通过亲身的试验、统计过程获得用试验方法估计复杂事件发生的概率的体验。

教学过程：第一环节创设情境引入新课师：（出示多媒体）历史上法国有位数学家布丰做了一个有趣的试验————投针试验。

他在地上以相同的距离a画了一些平行线，站在一定距离远处，从一定高度随意投掷一定长度l ( l＜a )的针，该针可能与其中一条平行线相交，也可能与它们都不相交。

你能不能通过列表或画树状图求出该针与平行线相交的概率？生：不能，因为相交与不相交的发生可能性不同。

师：那么，怎样才能得到它们与平行线相交的概率呢？生：作试验得到概率. 因为我们前面学过，当试验次数较大时，试验频率稳定于理论概率”。

师：好的，那么我们现在就通过试验，解决这个问题。

板书课题（6.2.投针试验）设计意图：通过问题激发学生，学习的兴趣。

为试验教学打下基础。

第二环节合作交流探求新知试验活动1：投针试验试验道具：牙签（用来替代针）、直尺、计算器、画有平行线的纸.试验准备：在大的白纸上画出间距等于牙签长度的2倍的一组平行线.试验要求：（1）一定距离外（2）一定高度（3）随意抛掷（4）投针100次为一次试验试验步骤：（1）同桌两人组成一个合作小组，一人投牙签，一人记录相交次数.（2）计算本组试验数据中牙签与平行线相交的频率.每小组数据统计表（3）汇总各组试验数据，计算牙签与平行线相交的频率，从而估计相交的概率。

投针试验投针问题1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的布丰投针问题。

投针步骤这一方法的步骤是：1）取一张白纸，在上面画上许多条间距为a的平行线。

2）取一根长度为l（l<a）的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为a的平行线，将一根长度为l（l<a）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。

”布丰本人证明了，这个概率是p=2l/（πd) π为圆周率利用这个公式可以用概率的方法得到圆周率的近似值。

下面是一些资料试验者时间投掷次数相交次数圆周率估计值Wolf1850年5000 2532 3.1596Smith 1855年3204 1218.5 3.1554C.De Morgan 1680年600 382.5 3.137Fox1884年1030 489 3.1595Lazzerini 1901年3408 1808 3.1415929Reina 1925年2520 859 3.1795设这三个正数为x，y，z，不妨设x≤y≤z，对于每一个确定的z，则必须满足x+y>z，x&sup2;+y&sup2；﹤z&sup2；，容易证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件，用线性规划可知满足题设的可行域为直线x+y=z与圆x&sup2;+y&sup2;=z&sup2；围成的弓形，总的可行域为一个边长为z的正方形，则可以围成一个钝角三角形的概率P=S弓形/S正方形=（πz&sup2;/4-z&sup2;/2）/z&sup2;=（π-2）/4.因为对于每一个z，这个概率都为（π-2）/4，因此对于任意的正数x，y，z，有P=（π-2）/4，命题得证。