2020北京试题研究课件·数学3.第32课时 切线的性质及判定

第六章 圆 第32课时 切线的性质及判定 (建议时间：45分钟)

基础过关 1. (2019重庆A卷)如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD，若∠C＝50°，则∠AOD的度数为( ) A.40° B.50° C.80° D. 100°

第1题图 2. (2019通州区期末)如图，PA和PB是⊙O的切线，点A和B为切点，AC是⊙O的直径，已知∠P＝50°，则∠ACB的大小是( ) A. 65° B. 60° C. 55° D. 50°

第2题图 3. (2019泰安)如图，△ABC是⊙O的内接三角形，∠A＝119°，过点C的圆的切线交BO于点P，则∠P的度数为( ) A. 32° B. 31° C. 29° D. 61°

第3题图 4. (2019贺州)如图，在△ABC中，O是AB边上的点，以O为圆心，OB为半径的⊙O与AC相切于点D，BD平分∠ABC，AD＝3OD，AB＝12，CD的长是( ) A. 23 B. 2 C. 33 D. 43 第4题图 5. 如图，PA与⊙O相切于点A，线段PO交⊙O于点C，过点C作⊙O的切线交PA于点B.若PC＝4，AB＝3，则⊙O的半径长为 .

第5题图 6. (2019北京四中月考)如图，PA，PB是⊙O的两条切线，切点分别为A，B.连接OA，OB，AB，PO，PO与AB交于点C.若∠APB＝60°，OC＝1，则△PAB的周长为 .

第6题图 7. (2019东城区二模)如图，⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC交BC的延长线于点D，∠ABC＝45°. (1)求证：AD是⊙O的切线；

(2)若sin∠CAB＝35，⊙O的半径为522，求AB的长.

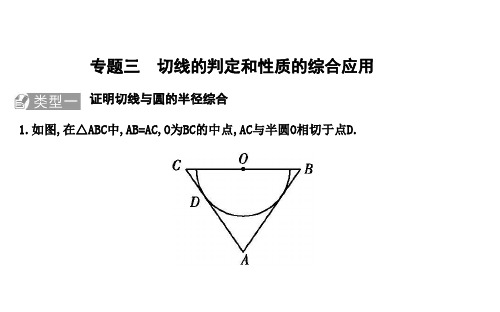
第7题图 8. (2020原创)如图，在平面内给定△ABC，点O到△ABC三个顶点的距离均等于c(c为常数)，到点O的距离等于c的所有点组成图形G，过点A作AB的垂线交BC于点E，交图形G于点D，延长DA，在DA的延长线上存在一点F，使得BF⊥OB，且∠ABF＝∠ABC. (1)求证：AB＝AC；

(2)若AD＝4，cos∠ABF＝45，求DE的长.

第8题图

能力提升 9. (2019海淀区期末)如图，在平面直角坐标系xOy中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ的最小值为 .

第9题图 10. (2018石景山区二模)如图，⊙O的半径为2，切线AB的长为23，点P是⊙O上的动点，则AP的长的取值范围是 .

第10题图 11. (2019朝阳区期末)如图所示的网格是正方形网格，线段AB绕点A顺时针旋转α(0°＜α＜180°)后与⊙O相切，则α的值为 . 第11题图 12. (2019房山区期末)如图①，将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形，CD⊥AB，垂足为D，半圆(量角器)的圆心与点D重合，此时，测得顶点C到量角器最高点的距离CE＝2 cm，将量角器沿DC方向平移1 cm，半圆(量角器)恰与△ABC的边AC，BC相切，如图②，则AB的长为 cm.

第12题图 满分冲关 13. (2019延庆区期末)如图，在Rt△ABC 中，∠C＝90°，∠A＝30°，AB＝43.若动点 D 在线段 AC 上(不与点 A、C 重合)，过点 D 作 DE⊥AC 交 AB 边于点 E.点 A 关于点 D 的对称点为点 F，以 FC 为半径作⊙C，当 DE＝ 时，⊙C 与直线 AB 相切.

第13题图 14. (2019西城区二模)如图，AB是⊙O的直径，CA与⊙O相切于点A，且CA＝BA.连接OC，过点A作AD⊥OC于点E，交⊙O于点D，连接D B. (1)求证：△ACE≌△BAD； (2)连接CB交⊙O于点M，交AD于点N.若AD＝4，求MN的长.

第14题图 参考答案 第32课时 切线的性质及判定 基础过关 1. C 【解析】由题意知∠BAC＝90°，∠C＝50°，∴∠B＝40°，∴∠AOD＝2∠B＝80°. 2. A 【解析】如解图，连接OB，∵PA、PB是⊙O的切线，∴OA⊥PA，OB⊥PB，∴∠OAP＝∠OBP＝90°，∴∠AOB＝360°－90°－90°－50°＝130°，∴∠OCB＝12 ×130°＝65°，即∠ACB＝65°.

第2题解图 3. A 【解析】如解图，设BP与⊙O交于点M，连接OC，CM.∵PC是切线，∴∠OCP＝90°.∵四边形ABMC是圆内接四边形，∠A＝119°，∴∠BMC＝180°－119°＝61°.∵OC＝OM，∴∠OCM＝∠OMC＝61°.∴在△COM中，∠COM＝58°.∴在△COP中，∠P＝180°－∠COM－∠OCP＝180°－58°－90°＝32°.

第3题解图 4. A 【解析】∵AD是⊙O的切线，∴OD⊥AD，在Rt△AOD中，AD＝3 OD，∴tan A＝ODAD ＝OD3OD ＝33 ，∴∠A＝30°，∴∠AOD＝60°，∵OD＝OB，∴∠ODB＝∠ABD＝12 ∠AOD＝30°，∵BD平分∠ABC，

∴∠CBD＝∠ABD＝30°，∴∠ABC＝60°，∴∠C＝90°. 在Rt△ABC中，sin A＝BCAB ，AB＝12，∴sin 30°

＝BC12 ，BC＝AB·sin A＝12×12 ＝6. 在Rt△CBD中，CD＝BC·tan 30°＝6×33 ＝23 .

5. 6 【解析】设⊙O的半径为r，由切线长定理得，BC＝BA＝3，∵BC是⊙O的切线，∴∠BCP＝90°，∴PB＝PC2＋BC2 ＝5，∴AP＝PB＋AB＝8，∵PA是⊙O的切线，∴∠OAP＝90°，∴AP2＋OA2＝OP2，即82＋r2＝(4＋r)2，解得：r＝6. 6. 63 【解析】∵PA，PB是⊙O的两条切线，∴OA⊥PA，OB⊥PB，OP平分∠APB，PA＝PB，∵∠APB＝60°，∴△PAB是等边三角形，AB＝2AC，PO⊥AB，∴∠PAB＝60°，∴∠OAC＝∠PAO－∠PAB＝90°－60°＝30°，∴AO＝2OC，∵OC＝1，∴AO＝2，∴AC＝3 ，∴AB＝2AC＝23 ，∴△PAB的周长＝63 .

7. 解：(1)如解图，连接OA， ∵∠ABC＝45°， ∴∠AOC＝2∠ABC＝90°， ∵AD∥OC， ∴∠DAO＝∠COA＝90°， ∵OA是⊙O的半径， ∴AD是⊙O的切线； (2)过C作CE⊥AB于E， ∵∠AOC＝90°，

AO＝OC＝522 ， ∴AC＝5， ∵∠AEC＝90°，

∴sin ∠CAE＝CEAC ＝35 ，

∴CE＝3，AE＝4， ∵∠CEB＝90°，∠ABC＝45°， ∴∠BCE＝45°， ∴CE＝BE＝3， ∴AB＝AE＋BE＝7.

第7题解图 8. (1)证明：根据题意作图如解图所示； ∵BF⊥OB， ∴∠ABF＝∠D，∴∠ABF＝∠C， ∵∠ABF＝∠ABC， ∴∠ABC＝∠C， ∴AB＝AC；

第8题解图 (2)解：如解图，连接BD，在Rt△ADB中，∠BAD＝90°， ∵cos ∠ADB＝ADBD ，∴BD＝ADcos ∠ADB ＝ADcos ∠ABF ＝445

＝5.

∴AB＝3. 在Rt△ABE中，∠BAE＝90°，

∵cos ∠ABE＝ABBE ，∴BE＝

ABcos ∠ABE ＝345 ＝154 .

∴AE＝（154）2－32 ＝94 ，

∴DE＝AD－AE＝4－94 ＝74 .

能力提升 9. 3 【解析】如解图，连接PQ、OP，∵直线OQ切⊙P于点Q，∴PQ⊥OQ，在Rt△OPQ中，OQ＝OP2－PQ2 ＝OP2－1 ，当OP最小时，OQ最小，当OP⊥直线y＝2时，OP有最小值2，∴OQ

的最小值为22－1 ＝3 .

第9题解图 10. 2≤AP≤6 【解析】如解图，连接OB，∵AB是⊙O的切线，∴∠OBA＝90°，∴OA＝AB2＋OB2 ＝4，当点P在线段AO上时，AP最小为2，当点P在线段AO的延长线上时，AP最大为6，∴AP的长的取值范围是2≤AP≤6. 第10题解图 11. 60°或120° 【解析】如解图，线段AB绕点A顺时针旋转α(0°＜α＜180°)后与⊙O相切，切点为C′和C″，连接OC′、OC″，则OC′⊥AB′，OC″⊥AB″，在Rt△OAC′中，∵OC′＝1，OA＝2，∴∠OAC′＝30°，∴∠BAB′＝60°，同理可得∠OAC″＝30°，∴∠BAB″＝120°，综上所述，α的值为60°或120°.

第11题解图 12. 23 【解析】如解图，设图中半圆的圆心为O，与BC的切点为M，连接OM，则OM⊥MC，∴∠OMC＝90°，依题意知道∠DCB＝30°，设AB为2x cm，∵△ABC是等边三角形，∴CD＝3 x cm，在题图①中，CE＝2 cm，∴半圆的半径为(3 x－2)cm，由解图可知OC＝(3 x－1)cm，∴sin ∠DCB＝OMOC ＝12 ，

∴3x－23x－1 ＝12 ，∴x＝3 ，∴AB＝2x＝23 cm.

第12题解图 满分冲关 13. 32 或332 【解析】如解图，过C作CH⊥AB于H，∵∠ACB＝90°，AB＝43 ，BC＝12 AB＝23 ，AC＝3 BC＝6，∴由三角形面积公式得：12 BC·AC＝12 AB·CH，解得CH＝3，分为两种情况：①如解图①，∵CF＝CH＝3，∴AF＝6－3＝3，∵A和F关于D对称，∴DF＝AD＝32 ，∵DE∥BC，

∴△ADE∽△ACB，∴DEBC ＝ADAC ，∴DE23 ＝326 ，DE＝32 ；