圆的切线性质与判定

圆的切线与切圆的性质与判定圆是几何学中的基本概念，它是由平面上离定点距离相等的所有点组成的集合。

圆具有许多独特的性质和特点，其中之一就是切线和切圆的性质。

本文将详细探讨圆的切线以及切圆的性质和判定。

一、切点及切线的定义和性质1. 切点的定义：对于给定的圆和平面上的一个点，如果这个点与圆上的某一点重合时，我们称这个点和这个圆相切，并把它们的重合点称为切点。

2. 切线的定义：过圆上一点的所有直线中，与该圆只有一个公共点的直线称为切线。

3. 切点与切线的性质：a) 切线与半径的关系：切线垂直于半径，并且切点和圆心之间的线段与切线垂直。

b) 切线之间的关系：如果两个切点重合，那么这两条切线互相垂直。

c) 切线上的弧度关系：切线上的两个弧度相等。

d) 直径与切线的关系：以切点为端点的切线与过切点的直径互相垂直。

二、切圆的性质与判定1. 切圆的性质：a) 切圆的直径与切点垂直。

b) 圆的切线与切圆的切点在一条直线上。

c) 切圆和切圆所在的切线的切点互相垂直。

d) 切点与切圆所在的切线的任意两个切点构成的三角形是等腰三角形。

2. 切圆的判定：a) 通过切点作圆的半径，并作与原圆作垂直的线，这条垂线与圆的交点即为切圆的圆心。

b) 切圆的半径与原圆的半径相等。

三、切线和切圆的应用1. 圆的切线和切圆的性质在几何证明和计算中具有重要的应用价值。

a) 运用切线和切圆的性质可以证明等腰三角形的性质，从而解决相关的问题。

b) 在圆的几何计算中，切线和切圆的性质可以用于求解圆的切线长度、切点坐标等相关问题。

2. 圆的切线和切圆的性质在工程和科学领域也有广泛的应用。

a) 在建筑设计中，切线和切圆的性质可以应用于拱门和圆顶的构建。

b) 在物理学中，切线和切圆的性质可以解释光的传播和反射等现象。

结论：圆的切线与切圆的性质和判定是几何学中重要的概念和定理，它们具有广泛的应用。

熟练掌握圆的切线与切圆的性质和判定，对于解决几何证明、计算和应用问题都具有重要的意义。

切线证明法切线的性质定理： 圆的切线垂直于经过切点的半径切线的性质定理的推论１: 经过圆心且垂直于切线的直线必经过切点． 切线的性质定理的推论２: 经过切点且垂直于切线的直线必经过圆心 切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线．切线长定理: 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

一、要证明某直线是圆的切线，如果已知直线过圆上的某一个点，那么作出过这一点的半径，证明直线垂直于半径．【例1】如图1，已知AB 为⊙O 的直径，点D 在AB 的延长线上，BD ＝OB ,点C 在圆上，∠CAB ＝30º．求证:DC 是⊙O 的切线．思路:要想证明DC 是⊙O 的切线，只要我们连接OC ，证明∠OCD ＝90º即可． 证明：连接OC ，BC ．∵AB 为⊙O 的直径，∴∠ACB ＝90º．∵∠CAB ＝30º，∴BC ＝21AB ＝OB ．∵BD ＝OB ，∴BC ＝21OD ．∴∠OCD ＝90º．∴DC 是⊙O 的切线．【评析】一定要分清圆的切线的判定定理的条件与结论，特别要注意“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则就不是圆的切线．【例2】如图2，已知AB 为⊙O 的直径,过点B 作⊙O 的切线BC ,连接OC ,弦AD ∥OC ．求证：CD 是⊙O 的切线．思路：本题中既有圆的切线是已知条件，又证明另一条直线是圆的切线．也就是既要注意运用圆的切线的性质定理，又要运用圆的切线的判定定理．欲证明CD 是⊙O 的切线，只要证明∠ODC ＝90º即可．图1图2证明：连接OD ．∵OC ∥AD ，∴∠1＝∠3，∠2＝∠4． ∵OA ＝OD ，∴∠1＝∠2．∴∠3＝∠4． 又∵OB ＝OD ，OC ＝OC ，∴△OBC ≌△ODC ．∴∠OBC ＝∠ODC ．∵BC 是⊙O 的切线，∴∠OBC ＝90º．∴∠ODC ＝90º． ∴DC 是⊙O 的切线．【例3】如图2,已知AB 为⊙O 的直径,C 为⊙O 上一点，AD 和过C 点的切线互相垂直，垂足为D ．求证:AC 平分∠DAB ．思路：利用圆的切线的性质--与圆的切线垂直于过切点的半径．证明：连接OC ．∵CD 是⊙O 的切线，∴OC ⊥CD ．∵AD ⊥CD ，∴OC ∥AD ．∴∠1＝∠2． ∵OC ＝OA ，∴∠1＝∠3．∴∠2＝∠3． ∴AC 平分∠DAB ．【评析】已知一条直线是某圆的切线时,切线的位置一般是确定的．在解决有关圆的切线问题时，辅助线常常是连接圆心与切点，得到半径，那么半径垂直切线．【例4】 如图1,B 、C 是⊙O 上的点，线段AB 经过圆心O ，连接AC 、BC ，过点C 作CD ⊥AB 于D ,∠ACD =2∠B ．AC 是⊙O 的切线吗？为什么？解：AC 是⊙O 的切线． 理由：连接OC , ∵OC =OB ， ∴∠OCB =∠B ．图3 OABCD2 31∵∠COD是△BOC的外角,∴∠COD=∠OCB+∠B=2∠B．∵∠ACD=2∠B，∴∠ACD=∠COD．∵CD⊥AB于D,∴∠DCO+∠COD=90°．∴∠DCO+∠ACD=90°．即OC⊥AC．∵C为⊙O上的点，∴AC是⊙O的切线．【例5】如图2,已知⊙Ｏ是△ABC的外接圆，AB是⊙Ｏ的直径,D是AB的延长线上的一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．求证：DE是⊙O的切线．证明:连接OC,则OA=OC，∴∠CAO=∠ACO，∵AC平分∠EAB，∴∠EAC=∠CAO=∠ACＯ,∴AE∥CO,又AE⊥DE，∴CO⊥DE，∴DE是⊙O的切线．二、直线与圆的公共点未知时须通过圆心作已知直线的垂直线段，证明此垂线段的长等于半径【例6】如图3，AB=AC，OB=OC，⊙O与AB边相切于点D．证明：连接OD，作OE⊥AC，垂足为E．∵AB=AC，OB=OC．∴AO为∠BAC角平分线，∠DAO=∠EAO∵⊙O与AB相切于点D，∴∠BDO=∠CEO=90°．∵AO=AO∴△ADO≌△AEO，所以OE=OD．∵OD是⊙O的半径,∴OE是⊙O的半径．∴⊙O与AC边相切．【例7】如图,在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.证明：连结OE,AD。

圆的切线与切点圆是几何学中的一种重要图形，它具有许多独特的性质和特点。

其中，圆的切线与切点是一个常见而重要的概念。

本文将介绍圆的切线及其与切点相关的性质和应用。

一、圆的切线的定义与性质1. 定义：在平面几何中，对于给定圆，经过圆上一点的直线称为圆的切线，该点称为切点。

2. 切线与切点的关系：切线与圆之间存在着唯一的切点，同样地，圆上的任意一条切线都有唯一的切点。

3. 切线的判定条件：圆上的切线与半径的关系是相切时垂直，相交时不垂直。

也就是说，切线和半径在相切的点处垂直，而在相交的点处不垂直。

4. 切线长度的性质：当直线与圆相切时，切线的长度等于半径的长度。

二、切线的求解方法根据圆的切线与切点的性质，我们可以采用以下两种方法来求解切线方程及切点坐标。

1. 几何法：几何法是通过直观的几何图形进行推导和证明的方法，可以用来求解切线的方程和切点坐标。

(1) 过给定点求切线：假设给定点为P(x0,y0)，圆的方程为(x-a)²+(y-b)²=r²。

我们可以通过作直角三角形来找到过点P的切线。

首先以点P为顶点，作一个垂直于切线的直角三角形，使得斜边的长度等于半径r。

然后，通过求解直角三角形的边长和斜边的斜率，可以确定切线的斜率和截距，从而得到切线的方程。

(2) 求切点坐标：给定圆的方程和切线的方程后，我们可以解方程组，得到切点的坐标。

2. 解析法：解析法是通过数学的代数计算和推导来求解切线的方程和切点坐标的方法。

通过已知圆的方程和切点的坐标，可以利用代数运算和几何推导得出切线的方程和切点的坐标。

三、切线与切点的应用1. 最短路径问题：在平面上给定两点A和B，其中A位于圆内，B 位于圆外。

我们需要找到一条通过圆上某一点P的切线，使得切点D 为A点与B点之间的最短路径。

这样，我们可以利用圆的切线与切点的性质，求得最短路径的长度和切点的坐标。

2. 光的反射与折射：光线在介质之间传播时，会发生反射和折射现象。

圆的切线知识点总结一、切线的定义在欧式几何中，对圆的切线有以下几种定义：1. 如果一条直线与圆相交于两点，那么这条直线就被称为圆的切线。

2. 一条直线与圆相交于圆上的一点，那么这条直线就是圆的切线。

3. 一条直线与圆相切于圆上的一点，且直线上的其他点都在圆的外部，那么这条直线就是圆的切线。

这三种定义表达了切线与圆的位置关系，指出了切线与圆的相交情况以及位置特征。

二、切线的性质1. 切线与半径垂直圆的半径与切线的交点处相互垂直。

2. 切线定理若直线l与圆相切于点P，直线l与直径所夹的角为直角。

3. 切线长度相等过圆外一点作一切线与圆相交于A、B两点，连接线A、B，若CA=CB，则线段CA与线段CB构成圆的切线。

4. 切线的判定若直线l经过圆外一点，分别与圆上两点A、B相连，若线段AB的中点恰好是圆心O，那么直线l即为圆的切线。

5. 切线的唯一性圆外一点到圆的切线唯一。

以上是切线的主要性质，这些性质在解题时常常起到重要的作用，特别是在证明几何问题时，能够帮助我们理解和应用切线的知识。

三、切线与圆的位置关系1. 内切线如果一条直线与圆相交于圆上的一点，但直线上的其他点都在圆的内部，那么这条直线就是圆的内切线。

2. 外切线如果一条直线与圆相交于圆上的一点，且直线上的其他点都在圆的外部，那么这条直线就是圆的外切线。

3. 相切线如果一条直线与圆相切于圆上的一点，且直线上的其他点都在圆的外部，那么这条直线就是圆的相切线。

切线与圆的位置关系在解题时十分重要，通过分析切线和圆的位置关系，可以帮助我们求解许多几何问题。

四、切线的判定方法1. 切线与圆的位置关系我们可以通过切线与圆的位置关系来判断一条直线是否为圆的切线，如切线的定义所述，可以分析直线与圆的相交情况以及位置特征来判定切线。

2. 对于圆外一点到圆的切线的判定，我们可以利用中位线作图，利用几何思维判定出直线是否为圆的切线。

3. 切线定理的应用切线定理是判定切线的重要原理之一，通过利用切线定理，可以判定一条直线是否为圆的切线。

切线的判定和性质
切线的性质与判定
1.主要性质
（1）切线和圆只有一个公共点；
（2）切线和圆心的距离等于圆的半径；
（3）切线垂直于经过切点的半径；
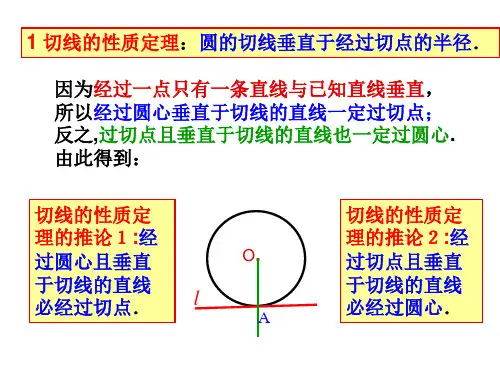
（4）经过圆心垂直于切线的直线必过切点；
（5）经过切点垂直于切线的直线必过圆心；
（6）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

其中（1）是由切线的定义得到的，（2）是由直线和圆的位置关系定理得到的，（6）是由相似三角形推得的，也就是切割线定理。

2.判定
切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

圆的切线垂直于这个圆过切点的半径。

圆的切线：切线的定义、性质和求解方法切线是与圆相切于一点且只与圆的该点相交一次的直线。

切线与半径垂直，也就是与半径所在的直径形成直角。

切线的定义给定一个圆，如果通过圆上的一点作两条直线，其中一条与半径垂直且只与该点相交一次，那么称这条直线为这个圆的一条切线。

切线的性质1. 切线与圆相切于一点，且只与圆的该点相交一次。

2. 切线与半径垂直，即与半径所在的直径形成直角。

3. 以切点为端点的切线被称为切线段。

4. 圆心到切点的线段被称为切线的斜率。

切线的求解方法求解圆的切线可以根据以下步骤进行：1. 给定一个圆和切点P，连接圆心O与切点P，得到半径OP。

2. 利用切线性质，使切线与半径OP垂直，得到直角三角形。

3. 根据已知条件，计算切线的长度。

切线的长度可以通过利用勾股定理或几何构造法进行计算。

勾股定理法求切线长度1. 已知圆的半径r和切点与圆心的连线OP的长度d。

2. 根据勾股定理，有切线长度s的平方等于d的平方减去圆的半径r的平方，即s^2 = d^2 - r^2。

3. 取根号可以得到切线的长度s。

几何构造法求切线长度1. 已知圆的半径r和切点与圆心的连线OP的长度d。

2. 以切点为圆心，作一条半径为r的圆。

3. 连接圆心与新圆上与切点P相对应的点Q，得到直角三角形OPQ。

4. 根据直角三角形OPQ中的三边关系，可以计算出切线的长度s。

这是圆的切线的定义、性质和求解方法的简要介绍。

掌握这些基本概念和求解方法，可以帮助我们更好地理解和应用切线在几何学中的重要性。