最新张量分析总结

第2章 张量分析§2.1矢量空间、基、基矢1．线性矢量空间设有n 个矢量,1,2,,i i n =a ，它们构成一个集合R ，其中每个矢量i a 称为R 的一个元素。

如()i j i j +≠a a 唯一地确定R 的另一个元素，及i k a （k 为标量）也给定R 内唯一确定的元素，则称R 为线性（矢量）空间。

R 中的零元素记为O ，且具有i ⋅=O a O .2．空间的维数设i α为m 个标量，若能选取i α，使得10mi ii =α=∑a且i α不合为零，则称此m 个矢量线性相关，否则，称为线性无关。

例1 位于同一平面内的两个矢量1a 和2a （如图）是线性无关的，即11220α+α≠a a 若1α和2α为任意值，且不全为零。

例2 位于同一平面内的三个矢量1a ，2a ，3a 是线性相关的，则恒可找到1α,2α,3α（不全为零）使1122330α+α+α=a a a 如图： 21133''=α+αa a a集合R 内线性无关元素的最大个数称为集合或空间的维数。

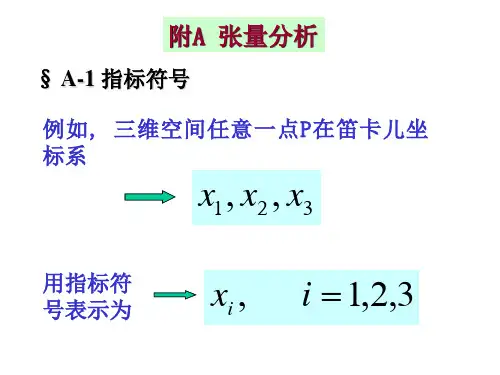
设R 的维数为n ，则记为n R ，欧氏空间为3R 。

3．空间的基和基元素n R 中任意n 个线性无关元素的全体称为n R 的一个基。

基的每个元素称为基元素，由于n R 的n 确良基元素是线性无关的。

于是n R 内任一个元素r 可表示成基元素的线性组合。

设(1,2,,)i i n =a 为n R 的任选的基，则有：10ni ii ='α≠∑a，i α'为任意的不全为零的标量但总可选取00≠α及i α不全等于零，使得010ni i i =α=α=∑r a或者2a1a21x2x3xi i x =r e110()nnii i i i i ==α=-=ξα∑∑r a a①i αα,00≠ 不全等于零，所以i ξ不全等于零，且为有限值。

② n R 内有无限个基，但只有一个基是独立的，因为n R 内至少只有n 个元素是线性无关的。

张量分析研一 熊焕君 2017.9.281.引论：我们对标量和矢量都非常熟悉。

标量是在空间中没有方向的量，其基本特征是只需要一个数就可以表示，且当坐标系发生转动时这个数保持不变，因此也称其为不变量。

而矢量是个有方向的量，三维空间中矢量需要一组三个数（分量）来表示，其基本特征是当坐标系发生转动时，这三个数按一定规律而变化。

然而在数学物理问题中，还常出现一些更为复杂的量，如描述连续体中一点的应力状态或一个微元体的变形特征等，仅用标量和矢量不足以刻画出他们的性质。

要描述这些量则有必要将标量和矢量的概念加以引申和扩充，即引入新的量——张量。

在概念上，张量和矢量有许多类同之处。

一方面张量也表示某一客观存在的几何量或物理量，显然张量作为一个整体是与描述它所选取的坐标系无关，可像矢量代数那样，用抽象法进行描述；另一方面也可像矢量一样采用坐标法进行描述，此时张量包含有若干个分量元素，各个分量的取值与具体的坐标系相关联。

张量的主要特征是，在坐标系发生变化时，其分量取值遵守着一定的转化定律。

张量方法的核心内容是研究一个复杂的量集坐标转换规律。

我们知道，一个物理定律如果是正确的，就必须不依赖于用来描述它的任何坐标系，张量方法就是既采用坐标系，而又摆脱具体坐标系的影响的不变方法。

于是我们可以在简单的直角坐标系中建立描述某一运动法则的支配方程，如果需要可以用张量方法将其转换到任意一个曲线坐标系中去。

例如对于很大一类边值问题，若选用恰当的曲线坐标系，其边界条件可以简化的表达，那么我们就可以将支配方程用张量方法转化到所采用的坐标系中来，从而使问题的求解容易处理。

2.记号与约定张量是包含有大量分量元素的复杂量集，必须使用适当的记号和约定，才能使其表达形式简化紧凑，从而使分析和讨论有序地进行。

从某种意义上讲，可以说张量是对记号的研究。

所以我们必须熟悉各种约定记号，才能对张量这个工具运用自如。

在张量方法中对一个量的标记采用字母标号法。

《连续介质力学》例题和习题第一张、矢量和张量分析第一节 矢量与张量代数一、 矢量代数令 11223A A A =++A e e e 112233B B B =++B e e e 则有 11223A A A αααα=++A e e e11122233()()()A B A B A B +=+++++A B e ee 1122331122331122()()A A A B B B A B A B A B ∙=++∙++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为 11⨯=e e 0 123⨯=e e e 132⨯=-e e e 213⨯=-e e e 22⨯=e e 0 231⨯=e e e 312⨯=e e e 321⨯=-e e e 33⨯=e e 0则 2332131132122(_)()()A B A B A B A B A B A B⨯=+-+-A B e e e习题1、证明下列恒等式：1）[]2()()()()⨯∙⨯⨯⨯=∙⨯A B B C C A A B C 2) [][]()()()()⨯∙⨯=∙⨯-∙⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 单位为正交的基矢量。

*补充知识：矩阵及矩阵运算1、定义：[]()111213212223313233,1,2,3ij A A A A A A A i j A AA ⎡⎤⎢⎥⎡⎤===⎣⎦⎢⎥⎢⎥⎣⎦A i 表示行，j 表示列；m 和n 相等表示为方阵，称为m （或n ）阶矩阵。