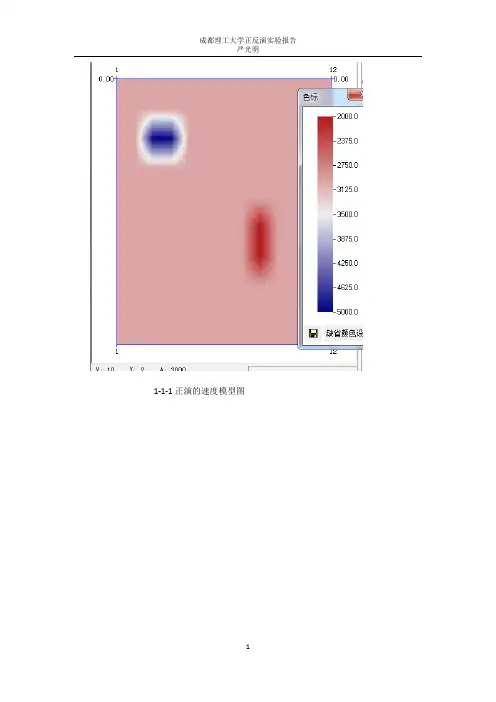
1-1-1正演的速度模型图图1-1-2分块均匀的模型1-2正演的后的走时图图1-3 反演前后速度对比图图1-5-a第0炮，第5接收点的数据图1-5-b-1正演第1炮，第8接收点（0为开始的激发点，0开始的接收点）图1-5-b-2 与1-5-b-2对应的验证图形（附注：由于本人u盘被病毒入侵，导致本人做得CAD图丢失，此图引用廖松杰同学的CAD图像，但是1-5-b-2由本人程序自己得出，特此说明。
）图1-5-c四边放炮，四边接收左方第2激发，图1-5-b单边接收第0炮，第25接收的r图像第5接收点的r数据图正反演的程序单边放炮单边接收：#include<stdio.h>#include<stdlib.h>#include<math.h>void fun1(int n,double R[144][108],double t[12][12]);void fun2(double k,double o,double t[12][12],double R[144][108],int m,int n);//k为斜率，o为炮点坐标，相当于截距；j；double fun(double x1,double y1,double x2,double y2);void main(){FILE *fp;int i,j,m,n,l,f;doublec[12],d[12],K[12][12],r[12][9]={0},v[12][9]={0.0},t[12][12]={0.0},u,o,w,R[144][108]={0. 0},k,v2[144]={0};float v1;//******************************************************************* ************************************//for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;}}v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{v2[j*12+i]=v[i][j];}}fp=fopen("速度","wb");for(i=0;i<12;i++){for(j=0;j<9;j++){v1=v[i][j];fwrite(&v1,sizeof(float),1,fp);}}fclose(fp);//******************************************************************* ************************************////************************************* 计算各点的斜率***************************************************//for(i=0;i<12;i++){//printf("第%d炮的斜率\n",i);c[i]=(i+0.5)*5.0;//*************************************************** ************激发点********//for(j=0;j<12;j++){d[j]=(j+0.5)*5;//**************************************************** *******接收点********//K[i][j]=(d[j]-c[i])/(9.0*3);//******************************************** **K斜率*********////printf("K[%d][%d]=%f\n",i,j,K[i][j]);}//printf("\n");}//******************************************************************* ***************************************//for(i=0;i<12;i++)//第i炮{for(j=0;j<12;j++)//第j接收点{if(K[i][j]==0)//平行于x轴,该行所在的每一个网格均经过,路程都是3{fun1(i,R,t);printf("t[%d][%d]=%f\n",i,j,t[i][j]);}else if(K[i][j]!=0){k=K[i][j];o=c[i];m=i;n=j;fun2(k,o,t,R,i,j);printf("t[%d][%d]=%lf\n",i,j,t[i][j]);}}}fp=fopen("time.txt","w");for(i=0;i<12;i++){for(j=0;j<12;j++){fprintf(fp,"%lf\n",t[i][j]);}}fclose(fp);fp=fopen("系数矩阵R的值.txt","w");for(i=0;i<144;i++){for(j=0;j<108;j++){fprintf(fp,"%f\t",R[i][j]);}fprintf(fp,"\n");}fclose(fp);fp=fopen("原来的速度值.txt","w");for(j=0;j<108;j++){fprintf(fp,"%f\t",v2[j]);}fclose(fp);}//******************************************************************* ***************************************////******************************************************************* ***************************************////*******************************当斜率k为0的时候，计算走时t的值********************************************////******************************************************************* ***************************************//void fun1(int n,double R[144][108],double t[12][12]){FILE *fp1;double b=0.0;int i=0,j=0,q=0;//循环变量double r[12][9]={0.0},v[12][9];//*************************************************************** for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;}}v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(j=0;j<9;j++){r[n][j]=3.0;}//******************************************************************* **////**********************写出检验r的值**********************************///*fp1=fopen("r的值.txt","w");for(i=0;i<12;i++){for(j=0;j<9;j++){fprintf(fp1,"%f\t",R[i][j]);}fprintf(fp1,"\n");}fclose(fp);*///******************************************************************* ****////******************************************************************* ****//for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{b+=r[i][j]*(1/v[i][j]);}}t[n][n]=b;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{R[n*12+n][q++]=r[i][j];}}}double fun(double x1,double y1,double x2,double y2){double s;{s=(y2-y1)*(y2-y1)+(x2-x1)*(x2-x1);return sqrt(s);}}//*****************************************************////******************************************************************* ***************************************//void fun2(double k,double o,double t[12][12],double R[144][108],int m,int n)//k为斜率，o为炮点坐标，相当于截距；{FILE *fp2;int i=0,j=0,q=0;;//循环变量int w1,w2,w3,w4;//中间变量，用来判断点在分块均匀上的位置double p=0,v[12][9]={0.0},r[12][9]={0.0};double x1,y1,x2,y2,x3,y3,x4,y4;float r1;//*************************************************************** v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;r[i][j]=0;}}for(i=0;i<12;i++){for(j=0;j<9;j++){y1=i*5.0;x1=(y1-o)/k;//计算交点1,由y计算x,交点一位于上边y2=(i+1)*5.0;x2=(y2-o)/k;//计算交点1,由y计算x，交点2位于下边x3=j*3.0;y3=k*x3+o;//计算交点3,由x计算y，交点3位于左边x4=(j+1)*3.0;y4=k*x4+o;//计算交点3,由x计算y，交点四位于右边//******************************************************************* ***//***判断射线是否经过分块均匀的网格点上,四个交点是否在网格的四条边上*****//**************************************************************** ******//***注意：网格的上下两条边y值相等,网格的左右两边x的值相等***************//**************************************************************** ******w1=(x1>=(j*3.0))&&(x1<=((j+1)*3.0))&&(y1==(i*5.0));//上方w2=(x2>=(j*3.0))&&(x2<=((j+1)*3.0))&&(y2==((i+1)*5.0));//下方w3=(y3>=(i*5.0))&&(y3<=((i+1)*5.0))&&(x3==(j*3.0));//左方w4=(y4>=(i*5.0))&&(y4<=((i+1)*5.0))&&(x4==((j+1)*3.0));//右方//**************************************************************** ******************//计算路径长度r，当有两个点存在时，有下面的六种情况。
