误差修正模型
- 格式:doc
- 大小:142.00 KB
- 文档页数:10

vecm 误差修正项系数是正数1.引言1.1 概述概述部分的内容应该简要介绍本篇长文的主题和背景,以引起读者的注意并为他们提供必要的背景信息。
概述部分的内容可以按照以下方式编写:引言:在经济领域的研究中,向量误差修正模型(Vector Error Correction Model,简称VECM)被广泛应用于协整关系的分析和预测。
VECM模型能够捕捉到经济变量之间的长期关系和短期调整过程,因此在经济学研究中扮演着重要的角色。
本文的目的是探讨VECM模型中的一个重要参数,即误差修正项系数。
传统上,人们认为误差修正项系数应该为负数,即用于恢复偏离均衡状态的力量。
然而,最近的研究表明,误差修正项系数可能是正数的情况也存在,并且在一些实证研究中得到了支持。
本文将重点分析正数误差修正项系数的可能原因,并探讨其对模型结果和政策决策的影响。
在接下来的章节中,我们将首先介绍VECM模型的理论背景,包括其基本原理和应用领域。
接着,我们将详细讨论误差修正项系数的概念和计算方法。
最后,我们将总结主要的研究发现,并探讨正数误差修正项系数的研究意义和未来的研究方向。
通过本文的研究,我们希望能够为经济学领域的研究者和从业者提供有关VECM模型和误差修正项系数的最新见解,促进相关领域的学术交流和经济政策的制定。
我们相信,对于VECM模型中误差修正项系数的深入研究将为我们对经济变量之间相互关系的理解提供更加全面和准确的认识。
此处简要介绍了本文的主题和背景,提出了正数误差修正项系数的研究目的,并概述了文章接下来的章节结构。
通过这种方式,读者可以对整篇文章的内容和结构有一个初步的了解,并对本文的研究意义产生兴趣。
1.2文章结构文章结构部分(1.2 文章结构):本文分为引言、正文和结论三个主要部分。
引言部分首先对文章进行了概述,介绍了研究的背景和动机。
随后,给出了文章的结构,即引言、正文和结论三个部分的内容安排。
最后,明确了本文的目的,即研究VEC模型中的误差修正项系数是否为正数。


协整与误差修正模型的研究第一部分协整理论概述 (2)第二部分误差修正模型介绍 (4)第三部分协整与误差修正关系 (7)第四部分模型构建与检验方法 (9)第五部分实证分析应用案例 (13)第六部分结果解释与经济含义 (16)第七部分模型局限性与改进方向 (18)第八部分研究展望与未来趋势 (22)第一部分协整理论概述协整理论概述在经济学和金融学中,我们常常遇到时间序列数据之间的长期均衡关系。
然而,在实际经济活动中,这种均衡关系并不总是能够得到严格的保持,而是存在着一定程度的波动和偏差。
为了解决这一问题,经济学家们提出了协整理论。
协整理论是指两个或多个非平稳的时间序列之间存在一种长期稳定的关系。
换言之,即使各时间序列本身是随机游走的过程,它们之间也可能存在一个稳定的线性组合,使得这个组合呈现出平稳性质。
协整理论的发展为研究经济变量之间的长期动态关系提供了一个强有力的工具。
协整理论的核心思想是由 Engle 和Granger 于1987 年提出的。
他们认为,如果两个非平稳的时间序列之间存在协整关系,则这两个时间序列可以通过一个线性组合达到长期均衡状态,且这个线性组合具有零均值、有限方差和恒定自相关等特性。
在这个意义上,我们可以将协整关系看作是一种长期均衡关系的表现形式。
为了检验两个时间序列之间是否存在协整关系,Engle 和 Granger 提出了一种两步法:首先检验每个时间序列是否为非平稳过程;然后,如果这两个时间序列都是非平稳过程,再通过回归分析来检验它们之间是否存在协整关系。
这种方法被称为 Engle-Granger 两步协整检验。
除了 Engle-Granger 两步协整检验之外,还有许多其他的方法可以用来检验协整关系,例如 Johansen 检验和 Pedroni 检验等。
这些方法都可以有效地帮助我们确定不同时间序列之间的协整关系。
协整理论不仅用于检验不同时间序列之间的长期均衡关系,还可以用于构建误差修正模型。

实验八:协整关系检验与误差修正模型(ECM)一、实验目的通过上机实验,使学生加深对时间序列之间协整关系的理解,能够运用Eviews 软件检验时间序列数据之间的协整关系并以此估计误差修正模型(ECM)。
二、预备知识(1)用EViews估计线性回归模型的基本操作;(2)时间序列数据的协整关系及其检验方法;(3)误差修正模型的结构及估计方法。
三、实验内容(1)用EViews检验两个时间序列数据的协整关系;(2)用EViews估计误差修正模型;四、实验步骤(一)、建立工作文件sy8.wf1及导入数据打开sy8.xls文件,运用前面学过的方法,在EViews新建一个工作文件sy8.wf1,把sy8.xls的数据导入到EViews,并根据得到人均消费(consp)和人均GDP(gdpp)两个序列,分别计算对应的自然对数,即lnc=log(consp)、lngdp=log(gdpp)。
(二)、分别检验序列lnc和lngdp的单整阶数。
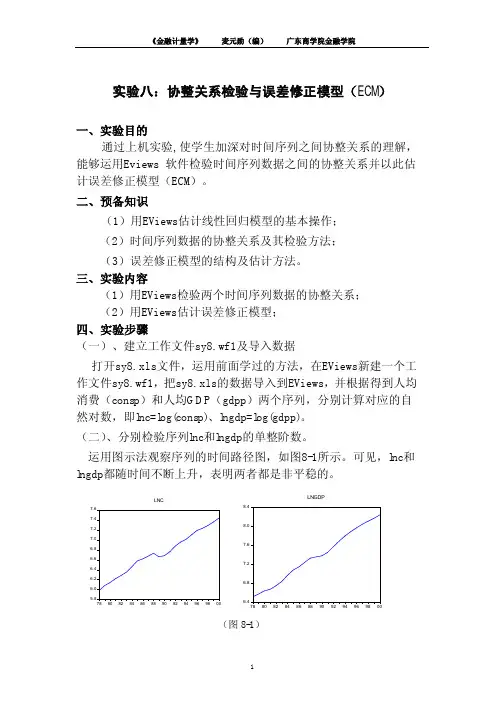
运用图示法观察序列的时间路径图,如图8-1所示。
可见,lnc和lngdp都随时间不断上升,表明两者都是非平稳的。
(再运用自相关函数法,判断lnc 的平稳性。
打开lnc 序列的窗口,点击view\Correlogram ,设定滞后阶数为12,可得样本自相关系数图,操作和结果分别如图8-2和图8-3所示。
可见,lnc 是非平稳的。
再分析lnc 的一阶差分是否平稳。
在自相关函数图中,设定显示序列的一阶差分(1st differenc )后,再观察其样本自相关函数图,设定和结果如图8-4和图8-5所示。
可见,lnc 取一阶差分后就达到平稳,因此,lnc 是一阶单整序列,即I(1)序列。
如果采用单位根检验,结果相同。
同理,也可检验得到lngdp 序列是I(1)序列。
(三)运用Engle-Granger 方法(即EG 检验)检验consp 与gdpp 的协整关系。
1、新建一个方程对象eq1,估计以下模型(结果如图8-6所示):01ln ln t t t c gdp ααµ=++ (8-1)2、在eq1窗口,点击Proc\Make Residual Series …,弹出Make Residual 窗口后,输入残差序列名称e ,再按OK 就把残差序列制成一个新的序列对象,见图8-7、图8-8。


实验报告(二)——误差修正模型(ECM)的建立与分析一、单位根检验:1、绘制cons与GDP的时间序列图:从时间序列图中可以看出,cons与GDP随时间增加都呈上升趋势,表现出非平稳性。
2、对cons进行单位根检验:先选择对原序列(level)进行单位根检验,根据cons与GDP的时间序列图的走势,选择trend and intercept的检验方法,在maximum lags中填写ADF 检验方法的滞后期为0,从上表中可以看出,P值为0.9888,大于0.05的显著性水平,说明原序列是非平稳的。
选择cons的一阶差分(1st)和trend and intercept,从上表中可以看出,经过一阶差分后,P值(=0.5099)仍然没有通过0.05的置信水平检验,说明是不平稳的,需要继续改进。
再试用ADF检验,在滞后期(maximum lags)中填入8,选择一阶差分和trend and intercept,得出上表,可以看出P值=0.0801,大于0.05,没有通过0.05的置信水平检验,说明是不平稳的,需要继续改进。
再试用ADF检验,在滞后期(maximum lags)中填入6,选择二阶差分和trend and intercept,得出上表,可以看出P值=0.0137,小于0.05,通过0.05的置信水平检验,说明是平稳的。
3、对GDP进行单位根检验:先选择对原序列(level)进行单位根检验,根据cons与GDP的时间序列图的走势,选择trend and intercept的检验方法,在maximum lags中填写ADF 检验方法的滞后期为0,从上表中可以看出,P值为1.0000,大于0.05的显著性水平,说明原序列是非平稳的。
选择GDP的一阶差分(1st)和trend and intercept,从上表中可以看出,经过一阶差分后,P值(=0.5574)仍然没有通过0.05的置信水平检验,说明是不平稳的,需要继续改进。

R语言向量误差修正模型(VECM)是一种用于多变量时间序列建模的方法,它可以帮助我们理解变量之间的长期和短期关系。
在本文中,我将深入探讨VECM模型的系数解读,并结合个人观点和理解,为您解析这一主题。
1. VECM模型简介VECM模型是向量自回归模型(VAR)的扩展,它在处理非平稳时间序列数据时具有很高的适用性。
与VAR模型不同的是,VECM模型考虑了变量之间的协整关系,从而可以分离长期均衡关系和短期动态调整过程。
2. VECM模型系数解读在VECM模型中,系数的解读非常重要。
我们需要关注模型的截距项和趋势项,它们代表了长期均衡关系的影响。
我们需要关注误差修正项的系数,它代表了模型中的短期调整过程。
通过这些系数的解读,我们可以更好地理解变量之间的动态关系。
3. 长期均衡关系解读当我们在VECM模型中发现存在协整关系时,我们可以通过截距项和趋势项来解读长期均衡关系。
截距项代表了长期均衡关系的水平,而趋势项则代表了长期均衡关系的变化趋势。
通过对这些系数的解读,我们可以揭示变量之间的长期关系。
4. 短期动态调整解读除了长期均衡关系,VECM模型还可以帮助我们理解变量之间的短期动态调整过程。
误差修正项的系数代表了短期动态调整的速度和方向,通过对这些系数的解读,我们可以了解变量之间的短期动态关系。
5. 个人观点和理解在我看来,VECM模型的系数解读是非常重要的。
通过深入理解模型系数的含义,我们可以更好地把握多变量时间序列数据的动态特性,从而做出更准确的预测和分析。
我认为在解读系数时,需要结合实际问题的背景和领域知识,以便更好地理解变量之间的关系。
总结与回顾通过本文的阐述,我们对VECM模型的系数解读有了更深入的理解。
从长期均衡关系到短期动态调整,每个系数都承载着丰富的信息,帮助我们理解变量之间的复杂关系。
在实际应用中,我们需要综合运用VECM模型的系数解读和领域知识,从而做出准确的预测和分析。
通过本文的讨论,相信您已经对r语言向量误差修正模型系数解读有了更深入的了解。

误差修正模型:如果用两个变量,人均消费 y 和人均收入x (从格林的数据获得)来研究误差修正模型。
令z=( y x )'则模型为:kL Z t 二 A o 二Z t二.7 PfZ tj 亠二i 4其中,二-「_'如果令k =1,即滞后项为1,则模型为L Z t = Ao• P^Z t 1 ■ ;t实际上为两个方程的估计:yt 二aybnyt □,皿人」-皿細」-Pi^":xtj ■ M t-x t - a x b 21 y t 1 b 22x t J ' p 21=y t二'p 22=x t 」■ ;2t用OlS 命令做出的结果:gen t=_n tsset ttime variable: t, 1 to 204 gen ly=L.y(1 miss ing value gen erated) gen lx=L.x(1 miss ing value gen erated) reg D.y ly lx D.ly D.lxNumber of obs = 202 F( 4, 197) =21.07Prob > F = 0.0000 R-squared = 0.2996Adj R-squared = 0.2854 Root MSE = 21.024D.y | + Coef. Std. Err. t P>|t| [95% Con f. I nterval] ly |.0417242.0187553 2.22 0.027 .0047371 .0787112 lx | -.0318574 .0171217-1.860.064-.0656228.001908 ly |D1. |.1093189.0823681.330.186-.0531173.2717552lx |D1. |.0792758 .0566966 1.40 0.164 -.0325344 .1910861cons |2.5335043.7571580.670.501-4.8759099.942916这是 y t ^a ybny t 4th 2x t 4' P 1「y t4 '卩册叹二’;1t的回归结果,其中 a y =2.5335,Source | +SSdfMSModel | 37251.2525 4 9312.81313 Residual | +87073.3154197 441.996525 Total | 124324.568201 618.530189b ii=0.04172, b i2= -0.03186 , p ii=0.10932, p i2=0.07928同理可得L x t= a x b2i y t j b22x td - p2i 二y t」-p2^x tJ■ ;2t的回归结果,见下reg D.x ly lx D.ly D.lxSource | SS df MS Number of obs = 202+ F( 4, 197)= 11.18 Model | 36530.2795 4 9132.56988 Prob > F = 0.0000Residual | 160879.676 197 816.648101 R-squared = 0.1850 + Adj R-squared = 0.1685Total | 197409.955 201 982.139082 Root MSE = 28.577D.x | ------------ +------- Coef. Std. Err. t P>|t|[95% Con if. Interval]ly 1 .037608 .0254937 1.48 0.142 -.0126676 .0878836 lx | -.0307729 .0232732 -1.32 0.188 -.0766694 .0151237ly 1D1. | .4149475 .111961 3.71 0.000 .1941517 .6357434 lx |D1. | -.1812014 .0770664 -2.35 0.020 -.3331825 -.0292203 _cons | 11.20186 5.10702 2.19 0.029 1.130419 21.27331如果用vec 命令vec y x, piVector error-correction modelSample: 3 - 204 No. of obs =AIC202 = 18.29975 = 18.35939 = 18.44715Log likelihood = -1839.275RMSE R-sq HQICSBICchi2 P>chi2Det(Sigma_ml) = Equation 277863.4 ParmsD_y 4 20.9706 0.6671 396.7818 0.0000D_x 4 28.5233 0.5328 225.8313 0.0000|-1-Coef. Std. Err. z P>|z| [95% Conf. Interval]D_y |_ce1 | L1.|x/ 1 .0418615 .0069215 6.05 0.000 .0282956 .0554273y |LD. | V 1 .1091985 .0807314 1.35 0.176 -.0490323 .2674292x |LD. | .0793652 .055411 1.43 0.152 -.0292384 .1879687_cons | --- + --- -3.602279 3.759537 -0.96 0.338-10.970843.766278D_x|_ce1 | L1.| y | LD. | V 1 .0256414 .0094143 2.72 0.006 .0071897 .044093 .4254495 .1098075 3.87 0.000 .2102308 .6406683x |LD. | -.1889879 .0753677 -2.51 0.012 -.3367058 -.04127 _cons | 5.880993 5.113562 1.15 0.250 -4.141405 15.90339这里_ce1 L1显示的是速度调整参数a的估计值,上述结果没有n的估计,而是在下面的表格中。


向量误差修正一 模型的概述1 VEC 模型向量误差修正模型VEC 是协整与误差修正模型的结合。
只要变量之间存在协整关系,就可以由自回归分布滞后模型导出误差修正模型,即VEC 模型是建立在协整基础上的V AR 模型,主要应用于具有协整关系的非平稳时间序列建模。
V AR 模型的表达式为:11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y ecm y x αΓH ε式中t y 为k 维内生变量列向量,其各分量都是非平稳的()1I 变量;t x 是d 维外生向量,代表趋势项、常数项等确定性项;每个方程都是一个误差修正模型,1t -ecm 是误差修正项向量,反映变量之间的长期均衡关系;系数矩阵α反映了变量之间偏离长期均衡状态时,将其调整到均衡状态的调整速度;解释变量的差分项的系数反映各变量的短期波动对作为被解释变量的短期变化的影响;t ε是k 维扰动向量。
2 诊断检验2.1 Johansen 协整检验Johansen 协整检验基于回归系数进行检验,其基本思想为: 对()VAR p 模型11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y ecm y x αΓH ε两端减去1t -y 再变形可以得到11=1=+++ =1, 2,, p t t i t i t t i t T ---∆∆∑y y y x ∏ΓH ε其中的,t ∆y t j -∆y ()=1,2,j p 都变为()0I 变量构成的向量,只要1t -∏y 是()0I 的向量,即1t -y 的各分量之间具有协整关系,就能保证t ∆y 是平稳过程,而这主要依赖于矩阵∏的秩。
设∏的秩为r ,则0<<r k 时才有r 个协整组合,其余k r -个关系仍为()1I 关系。
这种情况下,∏可以分解为两个k r ⨯阶矩阵α和β的乘积:=∏αβ'其中()()=,=r r r r αβ,则模型变为1'1=1=+++ =1, 2, , p t t i t i t t i t T ---∆∆∑y y y x αβΓH ε式中'1t -βy 为一个()0I 向量,β为协整向量矩阵,其每一列所表示的1t -y 的各分量线性组合都是一种协整形式,矩阵β决定了1t -y 的各分量之间协整向量的个数(r )与形式。
配对证券的修正误差模型关系在金融领域,配对交易是一种常见的交易策略,通过同时买入一个证券同时卖出另一个相关性较高的证券,以从它们之间的价格差异中获取利润。
然而,在实际交易中,由于各种因素的影响,配对证券之间的价格关系可能会出现偏离,即价格之间的差异不符合之前建立的模型。
因此,修正误差模型成为了研究配对证券关系的重要工具之一。
修正误差模型是一种用来描述两个或多个时间序列之间长期均衡关系的统计模型。
在配对交易中,我们通常会选取两只相关性较高的证券,假设它们之间存在着长期的均衡关系。
然而,由于市场波动、交易成本等原因,这种均衡关系可能会受到一定程度的干扰,导致价格之间的差异偏离了之前建立的均衡模型。
修正误差模型的基本思想是,在价格差异偏离均衡水平时,会产生一个误差项,该误差项会驱使价格回归到长期均衡状态。
具体来说,如果两只配对证券之间的价格差异超出了其正常的范围,就会出现修正误差,市场参与者会采取相应的交易策略来使价格回归到均衡水平。
这种修正过程可以通过统计模型来描述和分析,以帮助交易者更好地把握配对交易的机会。
修正误差模型通常包括了两个主要部分:协整关系和误差修正项。
协整关系用来描述两个时间序列之间的长期均衡关系,通过单位根检验等方法来确认证券之间是否存在协整关系;而误差修正项则用来描绘价格差异的短期波动,一旦价格偏离均衡水平,误差修正项会起到修正价格的作用,使其回归到长期均衡状态。
通过修正误差模型,交易者可以更准确地把握配对证券之间的价格关系,及时发现价格偏离并采取相应的交易策略。
在实际交易中,修正误差模型可以帮助交易者进行风险管理,提高交易的稳定性和盈利能力。
总的来说,修正误差模型为配对交易提供了一种有效的分析工具,帮助交易者更好地理解和利用配对证券之间的价格关系。
通过建立和分析修正误差模型,交易者可以更加精准地把握市场机会,提高交易的成功率和盈利能力。
因此,对于从事配对交易的交易者来说,熟练掌握修正误差模型的原理和应用是至关重要的。
建立误差修正模型的步骤
嘿,朋友们!今天咱来聊聊建立误差修正模型那些事儿。
你想想看啊,误差修正模型就像是给数据世界搭的一座稳固的桥。
咱为啥要建这座桥呢?就好比你走路,要是路坑坑洼洼的,你走得稳当吗?数据也是一样啊,有误差就得修正,不然得出的结果能靠谱吗?
那怎么建这座桥呢?首先啊,你得有数据,这就跟盖房子得有砖头一样。
你得仔细挑选那些有用的数据,把那些乱七八糟的杂质去掉。
然后呢,得观察这些数据的走势,就像你观察天气变化似的。
看看它们有没有啥规律,有没有啥特别的地方。
接着,开始构建模型啦!这就好像搭积木,一块一块地往上放,得放得恰到好处,不然就歪了倒了。
在这个过程中,你得不断地调整,这儿不合适就改改那儿,千万别嫌麻烦。
等模型搭得差不多了,就得测试一下啦!就跟新车得试驾一样,看看它能不能顺畅地跑起来。
要是有问题,赶紧回来再调整。
你说这麻烦不麻烦?哎呀,当然麻烦啦!但这可是为了得出准确的结果呀,咱可不能马虎。
再想想,要是医生看病不仔细,随便下诊断,那得多吓人啊!咱这建模型也是一样,得认真对待。
等你把模型建得稳稳当当的,那感觉,就像自己盖了一座漂亮的房子一样,特有成就感。
而且啊,以后再遇到类似的数据问题,你就可以轻松应对啦!
总之啊,建立误差修正模型可不是一件容易的事儿,但只要你有耐心,有细心,就一定能把这座桥搭好,让数据稳稳当当地通过。
别嫌麻烦,别偷懒,好好干,你一定能行的!。
第二节 误差修正模型(Error Correction Model ,ECM ) 一、误差修正模型的构造 对于y t 的(1,1)阶自回归分布滞后模型:
t t t t t y x x y εβββα++++=--12110
在模型两端同时减y t-1,在模型右端10-±t x β,得:
t
t t t t t t t t
t t t t x y x x y x y x x y εααγβεββββαββεββββα+--+∆=+---+--+∆=+-+++∆+=∆------)(])
1()1()[1()1()(1101012120120121100
其中,12-=βγ,)1/()(200ββαα-+=,)1/(211ββα-=。
记 11011-----=t t t x y ecm αα (5-5)
则 t t t t ecm x y εγβ++∆=∆-10 (5-6) 称模型(5-6)为“误差修正模型”,简称ECM 。
二、误差修正模型的含义
如果y t ~ I(1),x t ~ I(1),则模型(5-6)左端)0(~I y t ∆,
右端)0(~I x t ∆,所以只有当y t 和x t 协整、即y t 和x t 之间存在长期均衡关系时,式(5-5)中的ecm~I(0),模型(5-6)
两端的平稳性才会相同。
当y t 和x t 协整时,设协整回归方程为:
t t t x y εαα++=10
它反映了y t 与x t 的长期均衡关系,所以称式(5-5)中的ecm t -1是前一期的“非均衡误差”,称误差修正模型(5-6)中的1-t ecm γ是误差修正项,12-=βγ
是修正系数,由于通常1||2<β,这样0<γ;当ecm t -1 >0时(即出现正误差),误差
修正项1-t ecm γ< 0,而ecm t -1 < 0时(即出现负误差),
1-t ecm γ> 0,两者的方向恰好相反,所以,误差修正是一个反向调整过程(负反馈机制)。
误差修正模型有以下几个明确的含义:
1.均衡的偏差调整机制
2.协整与长期均衡的关系 3.经济变量的长期与短期变化模型
长期趋势模型:
t t t x y εαα++=10 短期波动模型:
t t t t ecm x y εγβ++∆=∆-10
三、误差修正模型的估计 建立ECM 的具体步骤为: 1.检验被解释变量y 与解释变量x (可以是多个变量)之间的协整性; 2.如果y 与x 存在协整关系,估计协整回归方程,计算残差序列e t :
t t t x y εβα++=0 t
t t x y e 0ˆˆβα--= 3.将e t-1作为一个解释变量,估计误差修正模型: t t t t v e x y ++∆=∆-10γβ 说明: (1)第1步协整检验中,如果残差是确定趋势过程,可以在第2步的协整回归方程中加入趋势变量; (2)第2步可以估计动态自回归分布滞后模型:
t i t i i t i t y x y εβαα∑∑+++=--
此时,长期参数为:
∑∑-=)1(i i βαθ
协整回归方程和残差也相应取成:
t t x y θ=, t
t t x y e θˆ-= (3)第2步估计出ECM 之后,可以检验模型的残差是否存在长期趋势和自相关性。
如果存在长期趋势,则在ECM 中加入趋势变量。
如果存在自相关性,则在ECM 的右端加入t t x y ∆∆和的滞后项来消除自相关性,误差修正项的滞后期一般也要作相应调整。
如取成以下形式: t t t t t t t t v e y x y x x y ++∆+∆+∆+∆+∆=∆-----1242312110γβββββ 由于模型中的各项都是平稳变量,所以可以用t 检验判断各项的显著性,逐个剔除其中不显著的变量,当然误差修正项要尽可能保留。
【例5-3】建立例5-2中我国货币供应量与国民收入的
误差修正模型。
协整关系。
在例5-2中已经得到我国货币供应量和国民收入的对数都是一阶单整变量,而且是协整的;所以,直接估计误差修正模型(设残差序列是t e ): LS D(LX) D(LX) E(-1) 估计结果如图5-9所示,误差修正项的符号是负的,但是t 检验不显著。
对模型的残差序列进行自相关检验,DW 检验和BG 检验结果都说明存在一阶自相关;所以,点击方程窗口的Estimate 按钮,在方程描述框中重新定义待估方程: D(LX) D(LX) E(-1) D(LX(-1)) D(LY(-1)) 根据输出结果,剔除其中不显著的1-∆t y ,得到图5-10的估
计结果。
模型中误差修正项的符号是负的,而且各项的t 检验显著,所以,我国货币供应量的误差修正模型为:
116716.0ln 1855.1ln 2922.2ln ---∆-∆=∆t t t t e x x y
(4.87) (-2.92) (-2.58) R 2=0.4693 SE =0.0603 D W =0.9649
图5-9 ECM 的最初估计结果
图5-10 ECM 的最终估计结果
案例分析:我国金融发展与经济增长的协整分析 表5-4中列出了1989~2006年期间我国国内生产总值指数(1978=100)、货币供应量M2(亿元)、金融机构年末贷款余额(亿元)和商品零售价格指数(1978=100)的统计资料。
现以货币供应量和贷款余额反映金融的发展情况,分析金融发展与经济增长的协整关系,以及相应的误差修正模型。
表5-4 我国1989~2006年统计资料 年份 国内生产总值Y 广义货币M2 贷款余额L 商品零售价格指数P 1989 271.3 12716.9 14360.1 203.4 1990 281.7 15293.4 17680.7 207.7 1991 307.6 19349.9 21337.8 213.7 1992 351.4 25402.2 26322.9 225.2 1993 400.4 34879.8 32943.1 254.9 1994 452.8 46923.5 39976.0 310.2 1995 502.3 60750.5 50544.1 356.1 1996 552.6 76094.9 61156.6 377.8 1997 603.9 90995.3 74914.1 380.8 1998 651.2 104498.86524.1 370.9
为消除价格因素的影响,将货币供应量M2和贷款余额L 都除以物价指数P ,得到实际货币量;同时为了将各项指标的变化趋势转变成线性趋势,对所有变量都取对数。
变量的处理过程为: GENR LY=LOG(Y) GENR LMP=LOG(M2/P) GENR LLP=LOG(L/P)
模型形式为:
t t P L P M Y εββα+++=)/ln()/2ln(ln 21
对模型中的变量进行单位根检验,表5-5列出了有关检验结果。
该表是另外一种常用的检验结果表现形式,其中,p 表示麦金农单侧概率值,即ADF 统计量对应的伴随概率;
在ADF统计量值上的*号,表示检验的显著情况:无*号表示不显著,***、**、*分别表示在1%、5%、10%的显著水平下显著。
表5-5的检验结果表明,所有变量都是确定趋势过程,此时不需要再对各个变量的一阶差分进行单位根检验了,即都~I(1)。
表5-5 单位根检验输出结果
2.协整性检验
估计协整回归方程,由于模型中变量都含有长期趋势,所以在原模型中再加上取食变量T,键入命令:LS LY
C LMP LLP T,估计结果如图5-11所示。
图5-11 协整回归方程估计结果(1)由于模型中LMP与LLP高度相关,多重共线性的影响使得贷款变量的系数符号为负,经济意义不合理。
经过多个模型的测算,最终将LMP与LLP合并成一个变量表示金融的发展规模,得到如图5-12所示的估计结果。
图5-12 协整回归方程估计结果(2)在方程窗口中点击Proc \Make Residual Series,生成
残差序列(设变量名为E );进一步检验残差序列的平稳性(检验结果见图5-13),在1%的显著水平下,残差序列是平稳的。
所以,根据EG 两步检验法,lnGDP 与实际货币和实际贷款(的对数)之间存在着协整关系。
协整回归方程为:
)ln (ln 3284.082.2ˆln LP MP Y t
++=
图5-13 残差序列E 的平稳性检验结果
3.建立误差修正模型
为表示简单起见,设:LX=LMP+LLP ;键入命令:
GENR LX=LMP+LLP
LS D(LY) E(-1)
输出结果显示E t-1的系数不显著,对模型进行残差检验,发
现存在一阶自相关性;所以,在模型中再加入LY 和LX 的滞后项,利用t 检验剔除不显著变量后,得到ECM 的最后估计结果(见图5-14)。
图5-14 ECM 的最终估计结果
所以,我国经济增长与金融发展的关系模型可以表述成: 长期均衡关系:
)ln 5559.0(ln 3284.082.2ˆln LP MP Y t
++= 短期波动模型:
21112431.0ln 5092.0)ln (ln 0618.0)ln (ln 1106.0ln -----∆++∆++∆=∆t t t t t t t e Y LP MP LP MP Y。