dd狭长矩形截面杆自由扭转的材料力学解法
- 格式:pdf
- 大小:79.19 KB
- 文档页数:2


钢结构抗扭设计的探讨摘要:本文通过阐述钢梁抗扭设计的材料计算公式,然后通过有限元软件进行计算和对比,并提出钢结构抗扭设计的建议,使得钢结构设计更加经济、安全和合理。
关键词:抗扭截面模量,抗扭刚度,有限元计算Abstract: This article elaborates on the material calculation formula for the torsional design of steel beams, and then uses finite element software to calculate and compare, and proposes suggestionsfor the torsional design of steel structures, making the design ofsteel structures more economical, safe, and reasonable.Keywords: torsional section modulus, torsional stiffness, finite Metacomputing.一、引言在建筑结构设计中,钢结构受力一般只需考虑受弯、受剪和轴力的计算,并且在钢结构设计规范中缺少抗扭计算公式(钢结构设计规范的征求意见稿曾给过)。
但是实际工程中,钢构件承受扭转是比较普遍的现象,而且往往与受弯同时作用。
结构设计师在设计中,有些会忽视抗扭计算,有些只是在构造上做一些处理,这样往往给结构设计带来安全隐患,也比较盲目。
本文从材料力学上介绍钢梁抗扭转的计算公式,并且采用有限元软件进行抗扭计算和对比,并提出钢结构抗扭设计的建议,供结构设计师及有关人员参考。
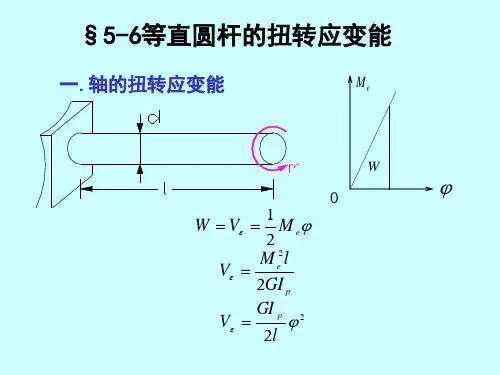
二、材料力学抗扭计算公式扭转变形是杆件的基本变形之一,它的荷载特征是,杆件受力偶作用,这力偶作用于与轴线垂直的平面内。
力偶矩矢方向可用右手螺旋法则确定。




§9.5 矩形截面杆的扭转学习思路:应力函数的确定是扭转应力解法的关键。
但是矩形横截面柱体的扭转问题不能采用与椭圆形截面柱体相同的方法建立扭转应力函数。
矩形截面柱体分析的第一步是引入特解,将基本方程—泊松方程简化为拉普拉斯方程。
第二步是将应力函数表达为坐标x和y的函数。
并且根据问题性质,简化应力函数,为求解级数形式表达的应力函数作准备。
第三步是根据面力边界条件确定级数形式的应力函数。
最后,根据应力函数求解横截面切应力表达式。
并且分析横截面切应力分布。
学习要点:1. 矩形截面柱体的扭转分析;2. 扭转应力函数;3. 扭转级数解;4. 矩形截面柱体扭转切应力;5. 横截面应力分析设矩形的边长为a和b,如图所示。
矩形截面杆件的扭转问题,不能像椭圆截面杆件扭转问题一样假设扭转应力函数为原因很简单,这个应力函数虽然满足ψc=0,但是泊松方程却不可能满足。
由于根据边界条件难以直接确定满足基本方程的扭转应力函数,因此首先简化扭转问题的基本方程。
对于扭转问题的应力解法,基本方程为泊松方程。
为了简化分析,需要找到泊松方程的特解,将基本方程转化为拉普拉斯方程。
因为拉普拉斯方程求解相对简单。
因为变形协调方程有一个特解,所以设则变形协调方程转化为对于柱体的侧面面力边界条件,ψc=0 ,则要求ψ0满足边界条件由于柱体横截面是关于坐标轴x和y对称的,而扭矩T是关于坐标轴反对称的,因此横截面切应力必然是与坐标轴反对称的。
所以,设扭转应力函数ψ 0(x,y)为代入变形协调方程,则将上式改写为,, 其中λ为任意常数。
根据所以根据薄膜比拟,矩形横截面切应力是坐标的奇函数,因此应力函数应该为坐标x和y的偶函数。
所以上式仅是方程的一个特解。
如果将所有特解作线性迭加就是方程的通解,所以 0(x,y)写作根据边界条件的第二式,有由于,所以。
因此,。
回代可得根据边界条件的第一式,有对于上式两边同时乘以,并在(-b,b)区间积分,可得所以,应力函数为根据应力函数表达式,应力分量为上式中的单位长度扭转角ϕ由端面面力边界条件确定,即对于上述级数,其收敛很快,取n=0一项分析,则根据切应力表达式,可以得到矩形横截面的应力分布,如图所示。

第四章 扭转§4—1 工程实例、概念一、工程实例1、螺丝刀杆工作时受扭。
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
4、钻井中的钻杆工作时受扭。
二、扭转的概念受力特点:杆两端作用着大小相等方向相反的力偶,且作用面垂直杆的轴线。
变形特点:杆任意两截面绕轴线发生相对转动。
轴:主要发生扭转变形的杆。
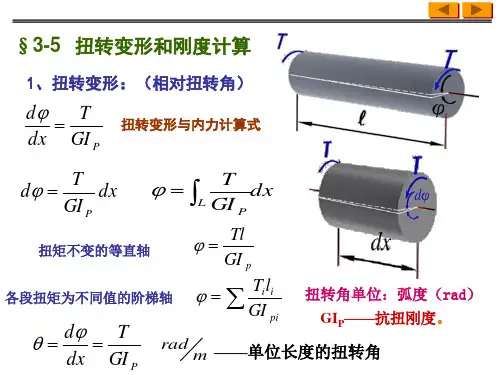
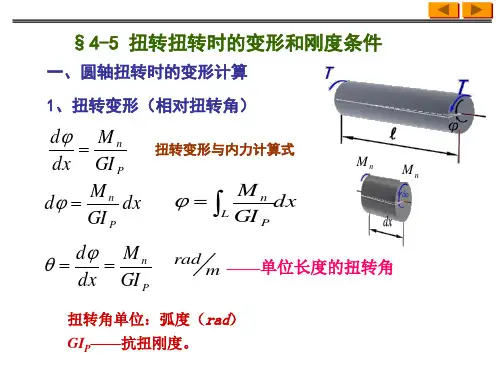
§4—2 外力偶矩、扭矩一、外力:m (外力偶矩)1、已知:功率 P 千瓦(KW ),转速 n 转/分(r /min ; rpm)。
外力偶矩:m)(N 9549⋅=nPm 2、已知:功率 P 马力(Ps),转速 n 转/分(r /min ;rpm)。
外力偶矩:m)(N 7024⋅=nPm 二、内力:T (扭矩) 1、内力的大小:(截面法)mT m T mx==-=∑002、内力的符号规定:以变形为依据,按右手螺旋法则判断。
(右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若其矢量方向背离所在截面则扭矩规定为正值,反之为负值。
)3、注意的问题:(1)、截开面上设正值的扭矩方向;(2)、在采用截面法之前不能将外力简化或平移。
4、内力图(扭矩图):表示构件各横截面扭矩沿轴线变化的图形。
作法:同轴力图:§4—3 薄壁圆筒的扭转 一、薄壁圆筒横截面上的应力(壁厚0101r t ≤,0r :为平均半径) 实验→变形规律→应力的分布规律→应力的计算公式。
1、实验:2、变形规律:圆周线——形状、大小、间距不变,各圆周线只是绕轴线转动了一个不同的角度。
纵向线——倾斜了同一个角度,小方格变成了平行四边形。
3、切应变(角应变、剪应变):直角角度的改变量。
4、定性分析横截面上的应力(1) 00=∴=σε ;(2)00≠∴≠τγ因为同一圆周上切应变相同,所以同一圆周上切应力大小相等。
⑶ 因为壁厚远小于直径,所以可以认为切应力沿壁厚均匀分布,而且方向垂直于其半径方向。

狭长矩形截面杆自由扭转的材料力学解法
孟宪红 白昭宇
(北京航空航天大学飞机设计与应用力学系固体所,北京100083)
摘要 以往矩形截面杆自由扭转问题的解仅在弹性力学中查到,本文从材料力学的教学法和便于应用的观点重新分析了该问题,得到了其材料力学的解,当6/≥b h 时,可以满足工程应用的精度要求。
关键词 狭长矩形截面杆,自由扭转,材料力学
众所周知矩形截面杆自由扭转问题的解可在弹性力学中查到。
为便于过程应用,
将其写成如下形式
2
max hb T ατ=∗,3hb
Tl βϕ=∗
(1) 其中,α,β与b h /=ϕ有关,并以表格形式给出。
若从材料力学的教学法和便于应用的观点考虑,用材料力学的方法来研究该问题仍有一定的价值。
为此,用材料力学的解法介绍如下。
1 应力分布
首先,我们将图示长为h ,宽为b 的狭长矩形截面杆的截面用一矩形ABCD 和两个半圆截面代替。
矩形ABCD 的长=12h
b h −,两半圆的半径2/b R =。
参考坐标
系如图
1所示。
图 1
根据余能概念我们设剪应力分布如下,在矩形部分截面内
)0(max
1R Y R
Y x ≤≤==τττ (2)
在半圆截面内
)0(max
2R r R
r
≤≤=ττ (3)
即剪应力在各部分均为线性分布, ⎪⎪⎭
⎪⎪⎬⎫
=−=θττθττcos sin max 2max 2R
r R
r y x (4)
在半圆内点的坐标均为
θθ
cos sin 1r h x r y +== (5)
2 确定max τ
由平衡条件,我们有
2
max 2
122max 12
max 2
2211161131)cos (cos sin )(12
2
1
hb dA r h R r R
r dA R y dA x y ydA T A A A y x A ⎭
⎬⎫⎩⎨⎧+⎟
⎟⎠⎞⎜⎜⎝⎛−=⎥⎦⎤
++⎢⎣⎡+=+−+=∫∫∫∫ςπςτθθθ
τττττ(6) 其中
b
h
=
ς (7) k
W T
hb T
=
⎥⎦
⎤⎢⎣⎡⎟
⎟⎠⎞⎜⎜⎝⎛−+=
2
max 113116ςςπτ (8) 2
113116hb W k ⎥⎦⎤⎢⎣
⎡⎟⎟⎠⎞⎜⎜⎝⎛−+=ςςπ (9) 3 求扭转角ϕ
杆件的余能
hb W T G l b b b h W T G l rdrd R r dydx R
y G l dV dV G dV G U k
k R R h V V V c ⎥⎦⎤⎢⎣
⎡⎟⎟⎠⎞⎜⎜
⎝⎛−+⎟⎟⎠⎞⎜⎜⎝⎛=
⎥⎦⎤
⎢⎣⎡+−⎟⎟⎠⎞⎜⎜⎝⎛=
⎭⎬⎫
+⎩⎨⎧=⎪⎭
⎪⎬
⎫⎪⎩⎪⎨⎧+==∫∫∫∫∫∫∫ςςππθττττπ11318232)(12124242122
22
02/022
0022
2max 22
21212
121(10)
⎪⎪⎪⎭
⎪⎪⎪⎪⎬⎫
⎥⎦⎤⎢⎣⎡⎟
⎟⎠⎞⎜⎜⎝⎛−+⎥⎦⎤⎢⎣
⎡⎟⎟⎠⎞⎜⎜⎝⎛−+==∂∂=
ςςπςςπϕ1131811311632
hb J GJ Tl T U k k
c (11) 4 精度分析
将式(8)、式(11)之结果与精确解式(1)两式对比可得其精度,max τ和ϕ的相对误差分别以r δ及ϕδ表示,则有
⎟⎟⎠
⎞⎜⎜⎝⎛−+−=−=∗
∗
ςςπ
α
τττδ1131161max max max r 2
113116113181⎥⎦⎤
⎢⎣
⎡⎟⎟⎠⎞⎜⎜⎝⎛−+⎥⎦⎤
⎢
⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−+−=−=∗∗
ςςπςςπ
βϕϕϕδϕ 其结果列于表1中。
表1
ς α
r δ β
ϕδ
1.0 0.208-5.93% 0.141 -43.6%
1.2 0.2190.08%0.166 -3
2.3%1.5 0.231 4.55%0.196 -24.8%1.75 0.239 6.30%0.214 -20.8%2.0 0.2467.11%0.229 -18.5%2.5 0.2587.37%0.249 -14.6%
3.0 0.2677.19%0.263 -12.2%
4.0 0.282
5.71%0.281 -9.37%
6.0 0.299 3.70%0.299 -6.44%8.0 0.307 2.91%0.307 -4.62%10.0 0.313 2.08%0.313 -3.94%∞ 0.333
0 0.333 0
由表1可知:当6/≥b h 时,用上述材料力学方法求得的max τ与ϕ可以满足工程应用的精度要求。
max τ稍小于∗
max τ,ϕ稍低于∗
ϕ。
参考文献
1 单辉祖主编.材料力学.北京:国防工业出版社,1995
2 徐芝纶.弹性力学.北京:高等教育出版社,1990。