当前位置：文档之家 › 矩形截面杆的扭转

矩形截面杆的扭转

  • 格式：doc
  • 大小：251.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

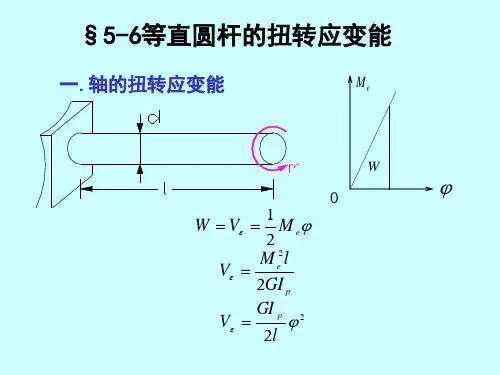
材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总

材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总
Me Tb Ta
( 4)
例题 6-6
5. 实心铜杆横截面上任意点的切应力为 Ta Ga M e 0 ra ρa I pa Ga I pa Gb I pb 空心钢杆横截面上任意 点的切应力为
b
Tb Gb M e I pb Ga I pa Gb I pb
2
1 dV (dxdydz ) 2 dV dW v dV dxdydz 1 v 2





一、密圈螺旋弹簧
——螺旋角
F
O

d
d ——簧丝横截面的直径 D ——弹簧圈的平均直径
O D
密圈螺旋弹簧 ——螺旋角<5°时的圆柱形弹簧
§4.5
密圈螺旋弹簧的计算
O F
例题 6-6
Me Tb Ta
解： 1. 实心铜杆和空心钢杆横截面上的扭矩分别为Ta 和Tb(图b)，但只有一个独立平衡方程 Ta+Tb= Me (1) 故为一次超静定问题。
例题 6-6
Me Tb Ta
2. 位移相容条件为实心杆和空心杆的B截面相对 于A截面的扭转角相等。在图b中都用表示（设 A端固定）。 Ba Bb ( 2)
a
b
ra
ra
a rb
切应力沿半径的变化 情况如图c所示。
ra
rb
(c)
§5-8非圆截面等直杆扭转的概念
圆截面杆扭转时的应力和变形公式,均建立在平 面假设 的基础上。对于非圆截面杆,受扭时横截面不 再保持为平面，杆的横截面已由原来的平面变成了曲 面。这一现象称为截面翘曲。因此,圆轴扭转时的应 力、变形公式对非圆截面杆均不适用。
(2)

第四章 扭转(张新占主编 材料力学)

第四章 扭转(张新占主编 材料力学)

2M A M e M B 0 （2）
联立式（1）与式（2），得
Me MB 3
MA MB Me 3
26
4.6 等直圆轴扭转时的应变能
圆轴在外力偶作用下发生扭转变形，轴内将积蓄应变能。这种 应变能在数值上等于外力所做的功。
T1 在位移 d1上所做的功为 dW T1d1
PB M eB M eC 9549 n 796(N m) PA M eA 9549 1910(N m) n PD M eD 9549 318(N m) n
5
（2）求扭矩（扭矩按正方向假设） 1-1 截面
M M M
x
0
T1 M eB 0
T1 M eB 796N m
d1 85.3 mm
取 d1 85.3 mm。 BC段：同理，由扭转强度条件得 d2 67.4 mm ，由扭转刚度条件得
d 2 74.4 mm
取 d 2 74.4 mm。
23
（2）将轴改为空心圆轴后，根据强度条件和刚度条件确定轴的 外径D。 由强度条件得 D 96.3 mm 由刚度条件得 D 97.3 mm 取 D 97.3 mm ，则内径为
T Me
M e RdA RRd 2R 2
A 0
2
Me 2 2R
8
二、切应力互等定理
M
z
0
（dy）dx （ dx）dy
得到

切应力互等定理：在单元体在相互垂直的一对平面上，切应力 同时存在，数值相等，且都垂直于两个平面的交线，方向共同 指向或共同背离这一交线。 纯剪应力状态：单元体上四个侧面上只有切应力，而无正应力 作用

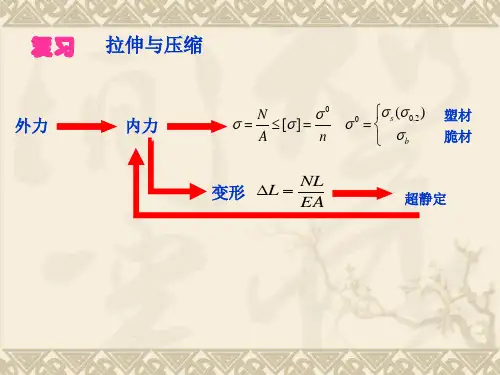
材料力学-第三章扭转

材料力学-第三章扭转

3、物理方程 mA a mA a AC 2GI p GI p
BC
2 mB a GI p
4 解得： m A 7 T 3 mB T 7
AB AC BC 0
例：由实心杆 1 和空心杆 2 组成的组合轴，受扭矩 T， 两者之间无相对滑动，求各点切应力。 T 解: 设实心杆和空心杆承担的扭矩分别为 G 2 Ip 2 M n 1 、 M n2 。 R2
二 刚度条件
M 180 刚度 n 0.50～1.0 / m 一般轴 l G Ip 条件

0.25～0.5 / m 精密轴
1.0 ～3.0 / m 粗糙轴
例 传动主轴设计，已知:n = 300r/m，P1 = 500kW，P2=200kW P3=300kW，G=80GPa [ ] 40MPa , [] 0.3 求：轴的直径d 解：1、外力分析




圆轴扭转的强度条件
max
Mn D Mn I p 2 Wp
Wp
2I p D
Mn
D 3 D 3 Wp 1 4 抗扭截面系数Wp : W p 16 16


强度条件：
Mn max Wp
例 已知汽车传动主轴D = 90 mm, d = 85 mm [ ] 60MPa, T = 1.5 kNm
Mn d
3
圆形优于矩形
Aa
= 0.208
3
a
3

4
3
d 0.886 d
2
Mn
a
2

Mn 0.208 0.886 d
b
6.913

材料力学-扭转

材料力学-扭转

扭转角（ 扭转角（ϕ）：任意两截面绕轴线相对转动的角度。又称为角 位移。通常用ϕ表示。ϕB − A表示B截面相对A截面转过的角度。 剪应变（ 剪应变（γ）： 剪应变又叫角应变或切应变，它是两个相互垂直方 向上的微小线段在变形后夹角的改变量（以弧度表示， 角度减小时为正） O ϕ B m
A m
γ
第二节 杆受扭时的内力计算
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面： 实心圆截面：
2
I p = ∫ ρ d A = ∫ ρ (2 πρ d ρ )
2
ρ
d O
dρ
A
d 2 0
= 2 π(
ρ
4
d /2
4
)
0
πd = 32
4
d A = 2 πρ d ρ
πd 3 Wp = = d / 2 16 Ip
空心圆截面： 空心圆截面：
T T = ρ max = IP IP T = WP
ρ max
Ip—截面的极惯性矩， 截面的极惯性矩，单位： 单位：m 4 , mm 4 Ip 3 3 WP —抗扭截面模量， WP = 抗扭截面模量，单位：m , mm .
ρ max
整个圆轴上——等直杆： 等直杆： τ max
Tmax = WP
三、公式的使用条件： 公式的使用条件： 1、等直的圆轴， 等直的圆轴， 2、弹性范围内工作。 弹性范围内工作。
Tmax Wp
πD 3 实心, 16 T max W = 2）设计截面尺寸: 设计截面尺寸:WP ≥ 3 P [τ ] πD (1 − α 4 ) 空心. 16 ≤ ⇒ m 3）确定外荷载: 确定外荷载: Tmax WP ⋅ [τ ]
≤

材料力学-扭转

材料力学-扭转
8
从圆轴中取一微小的正六面体（单元体）， 其对称两面上的剪应力构成一个力偶，因此 另两个对称面上也必存在转向相反的、由 剪应力构成的力偶。由此得出， 剪应力互等定理： 两个相互垂直的截面上，在其相交处的 剪应力成对存在，且其数值相等而符号相反， 指向或背离交线。 剪应力符号规定： 使单元体产生顺时针方向转动趋势时的剪应力为正 使单元体产生反时针方向转动趋势时的剪应力为负
§7-4 圆轴扭转时的强度计算
要使圆轴杆件扭转时不致产生破坏，应满足各横截面上的最 大剪应力小于材料的许用剪应力，而最大剪应力发生在扭矩最大 的横截面上的边缘处。设圆周半径为R，则圆轴扭转的强度条件 为：
τmax
T = R ≤ [τ ] Ip
Wp =
Ip R
把与截面尺寸和形状有关的参量归到一个参量，令 T 则有：
T ρ ρ 由此，圆轴扭转时横截面上半径为 处的剪应力为：τ ρ = Ip 4、极惯性矩 I 的计算 p πD 4
dϕ T = dX GI p
I p = ∫ ρ dA
2 A
直径为D的实心轴圆截面： I p = 空心轴圆环截面：I p =
π (D 4 − d 4 )
32
32
例：一轴AB传递的功率为Nk=7.5kw， 转速n=360r/min，轴的AC段为实心圆截面， CB段为空心圆截面，如图。已知D=3cm, d=2cm.试计算AC段横截面边缘处的剪应力 以及CB段横截面上外边缘和内边缘处的剪应力。计算扭矩、惯性矩、应力
Wp
≤ [τ ]
Wp
， 称为抗扭截面系数
Wp = 0.2D3
实心圆：
许用剪应力的确定：料 [τ ] = (0.5 ~ 0.6)[σ] 塑 材 ： 性 一般取 脆 材 ：τ ] = (0.8 ~1.0)[σ] 性 料 [

【工程力学】扭转变形【工程类精品资料】

【工程力学】扭转变形【工程类精品资料】

第四章扭转4.1预备知识一、基本概念 1、扭转变形扭转变形是杆件的基本变形之一，扭转变形的受力特点是：杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴。

此时，截面B 相对于截面A 转了一个角度ϕ，称为扭转角。

同时，杆件表面的纵向直线也转了一个角度γ变为螺旋线，γ称为剪切角。

2、外力偶杆件所受外力偶的大小一般不是直接给出时，应经过适当的换算。

若己知轴传递的功率P(kW)和转速n(r/min)，则轴所受的外力偶矩)(9549Nm nPT =。

3、扭矩和扭矩图圆轴扭转时，截面上的内力矩称为扭矩，用T 表示。

扭矩的正负号，按右手螺旋法则判定。

如扭矩矢量与截面外向法线一致，为正扭矩，反之为负；求扭矩时仍采用截面法。

扭矩图是扭矩沿轴线变化图形，与轴力图的画法是相似 4、纯剪切切应力互等定理单元体的左右两个侧面上只有切应力而无正应力，此种单元体发生的变形称为纯剪切。

在相互垂直的两个平面上，切应力必然成对存在且数值相等，两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线，这就是切应力互等定理。

5、切应变剪切虎克定律对于纯剪切的单元体，其变形是相对两侧面发生的微小错动，以γ来度量错动变形程度，即称切应变。

当切应力不超过材料的剪切比例极限时，切应力τ和切应变γ成正比，即τ=G γG 称材料的剪切弹性模量，常用单位是GPa 。

6、圆杆扭转时的应力和强度计算(1)圆杆扭转时，横截面上的切应力垂直于半径，并沿半径线性分布，距圆心为ρ处的切应力为ρτρpI T =式中T 为横截面的扭矩，I p 为截面的极惯性矩。

(2)圆形截面极惯性矩和抗扭截面系数图实心圆截面324D I p π=，163D W p π=（D 为直径） 空心圆截面)1(3244a D I p -=π，)1(1643απ-=D W p（D 为外径，d 为内径，D d /=α）(3)圆杆扭转时横截面上的最大切应力发生在外表面处tW T =m ax τ 式中W t =I p /R ，称为圆杆抗扭截面系数（或抗抟截面模量）。

材料力学 扭转3


T i L i j = å i (GI P )i
二、刚度条件 对于传动轴，有时即使满足了强度条件，还不一定能保证它 正常工作。例如：机器的传动轴如有过大的扭转角，将会使机器 在运转中产生较大的振动；精密机床上的轴若变形过大，则将影 响机器的加工精度等。因此对传动轴的扭转变形要加以限制。 一般地说：标志杆件扭转变形的物理量有两个： 绝对扭转角 相对扭转角
4
d 2 = 76 mm
5.选同一直径时
d = d . 4 mm 1 = 86
d1
6.将主动轮按装在 两从动轮之间
C
M e 2
(- )
d 2 B
M e 3
A
M e 1
4580 N × m 7640 N × m
d1 C
受力合理
M e 2
A
M e 1
1.5kN∙m
j AC = j AB + j BC = 0. 0239 rad 0318 rad - 0 . 0079 rad = 0.
&
例题2
M 2
图示一空心传动轴，轮1为主动轮，力偶矩M1＝9KN∙m，轮2、轮 3、轮4为从动轮,力偶矩分别为M2＝4KN∙m，M3＝3.5KN∙m，M4＝ 1.5KN∙m。已知空心轴内外径之比d/D＝1/2，试设计此轴的外径D，并 求出全轴两端的相对扭转角φ24。G＝80GPa，［τ］＝60MPa。
t t¢
等直圆杆扭转时的应变能
x
dx
2 2
V e dAdx e = ò v e dV = ò ò v
V l A
1 = tg g 2
Tr = I P
=

内容提要矩形截面直杆的扭转

第十二章 扭转与弯曲的几个补充问题一、 内容提要1. 矩形截面直杆的扭转 ab c t W 1max τντ= （12.2）杆件上相距为l 的两截面相对扭转角为3tTl TG hb GI ϕβ== （12.3） 3t I h b β=t I 称为矩形截面的扭转惯性矩。

以上各式中的系数α、ν、β和矩形截面的长边与短边的比值/h b 有关，其数值已列入教材表12.1中。

当h b >10时，截面成狭长矩形。

这时13αβ=≈。

如以δ狭长矩形的短边长度，则tW 和t I 分别为2t 13W h δ= ， 3t 13I h δ= （12.4）2．薄壁杆件的自由扭转 a ． 开口薄壁杆件的自由扭转由图12.4所示，开口薄壁截面可以看成若干狭长的矩形所组成的组合截面，则截面扭转惯性矩为3t t 1113nn i i i i i I I h δ====∑∑ （12.5）组合截面的最大切应力将发生在壁最厚的矩形的长边上，其值为maxmax tT I δτ=（12.6） 对于各种型钢，由于圆角及壁厚不均匀的影响，t I 还要给予修正，其修正公式为3t 113n i i i I h ηδ==∑b ．闭合薄壁杆件的自由扭转其横截面上任意一点处切应力的计算公式为02TA τδ=（12.7） 式中0A 为薄壁中线所围成的面积，δ为该点处的壁厚。

由于壁厚δ沿中线是变化的，则最大切应力应发生在壁厚最薄处，即max 0max2TA τδ=（12.8）闭合薄壁杆件上相距为l 的两截面相对扭转角为2d 4sTl sGA ϕδ=⎰（12.9）若杆件的壁厚δ不变，上式化为3．非对称弯曲情况。

纯弯曲力偶矩在xy当前讨论的纯弯曲问题，仍采用§3.8中提出的两各假设，即⑴平面假设；⑵纵向纤维间无正应力。

从而可推得在xy 平面内作用纯弯曲力偶矩z M 时，横截面上任一点的正应力为2()z y yz y z yzM I y I z I I I σ-=- （12.12）同理可得在xz 平面内作用纯弯曲力偶矩y M 时，横截面上任一点的正应力为2()y z yz y z yzM I z I y I I I σ-=- （12.13）对于一般性问题，即在包含杆件轴线得任意纵向平面内，作用一对纯弯曲力偶M 。

矩形截面杆、薄壁杆的扭转

面的扭转应力函数F(x,y)要满足的条件 ：
1、泊松方程：2F 2 (在柱形杆横截面所组成区域R内)。
2、边界条件：F(x, y) k（在横截面的周界C上）。
对于矩形截面杆件的扭转问题，能否像椭圆截面杆件扭 转问题一样假设扭转应力函数为其横截面的周界方程 ？
3 a2
a2
a3
a3
图3
设 ai 及 i分别表示扭杆横截面的第i个狭矩形的长度和宽度，
Ti表示该矩形截面上承受的扭矩，T表示整个横截面上的扭矩， i代表该矩形长边中点附近的剪应力， 为单 位长度扭转角。则
由狭长矩形的结果，得
3Ti
Gai
3 i
(2-1)
由式(2-1)得
i
3Ti
ai i 2
(2-2)
4G
13s2
A2 1
2
3
s1
A2 2
12s3 (
A1
A2
)2
(2-14) (2-15) (2-16)
例2 两个截面完全相同的变厚度薄壁杆如图8所示，其
中（a）为闭口，（b）为开口，试分析两杆件在抗扭转 刚度和最大剪应力方面的特点。
解（1）开口薄壁杆
由式(2-6),得单位长度扭转角：
G
3T
ai
1
4
T
图4
(2-6)
T
T
(2-6)
T
(2-6) T
(2-6) T
二 闭口薄壁杆件的扭转
对于闭口薄壁杆件的扭转问题，可以通过薄膜比拟
法求得近似解答。如图5所示，假想在薄杆横截面的外边
界上张一张膜，保证薄膜外边界的垂度为零，内边界处
的垂度为常量。由于杆壁厚度很小，所以沿壁的厚度方

工程力学3_6_5 矩形截面杆件的扭转


6.2 如图6-18所示为一拉杆头部，已知D=32mm，d=20mm， h=12mm，杆件材料的许用切应力［τ］=100MPa，许用挤 压应力［σbs］=240MPa。试校核该杆的剪切强度和挤压强 度。
6.3 如图6-19所示，两矩形截面木杆，用两块钢板连接。 截面的宽度b=200mm，沿拉杆顺纹方向承受拉力F=35kN， 木材的顺纹许用挤压应力［σbs］=8MPa，顺纹许用切应力 ［τ］=100MPa。求接头处所需的尺寸l和a。
6.6 如何计算扭矩？扭矩的正负号如何规定？ 6.7 圆轴扭转时，横截面上产生什么应力？如何计算？试 给出分布图。 6.8 横截面面积相同的情况下，空心轴与实心轴哪个抗扭 强度高？ 6.1 一托架如图6-17所示，铆钉和钢板之间为搭接。已知 铆钉的直径d=20mm，外力F=35kN。试求最危险的铆钉剪 切面上切应力的数值及方向。
6.4 如图6-20所示铆接接头。已知：板宽b=200mm，主板 厚t1=20mm，盖板厚t2=20mm，铆钉直径d=30mm，接头所 受拉力F=400kN，板与铆钉的材料相同。试计算： 6.5 如图6-21所示，传动轴以200r/min的转速匀速转动， 主动轮B的输入功率为60kW，从动轮A、C、D、E的输出功 率分别为18kW、12kW、22kW、8kW。试作轴的扭矩图。 6.6 如图6-22所示，传动轴的直径为100mm，已知MA=1k N·m，MB=2kN·m，MC=3.5kN·m，MD=0.5kN·m，［τ］=60M Pa。试作扭矩图，并校核该轴的强度。
6.5 矩形截面杆件的扭转
4.扭矩T是受扭构件横截面上分布内力系的合力偶矩，是由作用 在与杆轴线垂直的横截面上的外力偶矩引起的，正负号按右手 螺旋法则确定，即让右手四指沿扭矩的转向握住圆杆，若拇指 的指向离开截面向外扭矩为正，反之为负。 5.受扭圆轴横截面上任一点的切应力与该点到圆心的距离成正 比，圆心处切应力为零，最大切应力出现在圆轴边缘各点处。 6.等直圆轴扭转时的强度条件为 7.矩形截面杆件扭转变形后横截面产生翘曲现象，不再保持为 平面。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§9.5 矩形截面杆的扭转
学习思路:
应力函数的确定是扭转应力解法的关键。

但是矩形横截面柱体的扭转问题不能采用与椭圆形截面柱体相同的方法建立扭转应力函数。

矩形截面柱体分析的第一步是引入特解，将基本方程—泊松方程简化为拉普拉斯方程。

第二步是将应力函数表达为坐标x和y的函数。

并且根据问题性质，简化应力函数，为求解级数形式表达的应力函数作准备。

第三步是根据面力边界条件确定级数形式的应力函数。

最后，根据应力函数求解横截面切应力表达式。

并且分析横截面切应力分布。

学习要点：
1. 矩形截面柱体的扭转分析；
2. 扭转应力函数；
3. 扭转级数解；
4. 矩形截面柱体扭转切应力；
5. 横截面应力分析
设矩形的边长为a和b，如图所示。

矩形截面杆件的扭转问题，不能像椭圆截面杆件扭转问题一样假设扭转应力函数为
原因很简单，这个应力函数虽然满足ψc＝0，但是泊松方程却不可能满足。

由于根据边界条件难以直接确定满足基本方程的扭转应力函数，因此首先简化扭转问题的基本方程。

对于扭转问题的应力解法，基本方程为泊松方程。

为了简化分析，需要找到泊松方程的特解，将基本方程转化为拉普拉斯方程。

因为拉普拉斯方程求解相对简单。

因为变形协调方程有一个特解，所以设
则变形协调方程转化为
对于柱体的侧面面力边界条件，ψc＝0 ，则要求ψ0满足边界条件
由于柱体横截面是关于坐标轴x和y对称的，而扭矩T是关于坐标轴反对称的，因此横截面切应力必然是与坐标轴反对称的。

所以，设扭转应力函数ψ 0(x,y)为
代入变形协调方程，则
将上式改写为，, 其中λ为任意常数。

根
据
所
以
根据薄膜比拟，矩形横截面切应力是坐标的奇函数，因此应力函数应该为坐标x和y的偶函数。

所以
上式仅是方程的一个特解。

如果将所有特解作线性迭加就是方程的通解，所以 0(x,y)写作
根据边界条件的第二式，有
由于，所以。

因此，。

回代可得
根据边界条件的第一式，有
对于上式两边同时乘以，并在（-b，b）区间积分，可得
所以，应力函数为
根据应力函数表达式，应力分量为
上式中的单位长度扭转角ϕ由端面面力边界条件确定，即
对于上述级数，其收敛很快，取n=0一项分析，则
根据切应力表达式，可以得到矩形横截面的应力分布，
如图所示。

最大切应力发生在矩形长边的中点，即
根据公式,可得单位长度扭转角
和最大扭转切应
力
其中,β 和γ都是仅与比值a/b 有关的参数，这两个因子通过计算可以表示如下：
§9.6 开口薄壁杆的扭转
学习思路:
狭长矩形是指矩形横截面的一边长度远大于另外一边，这个问题有明显的工程意义。

工程结构中广泛使用的形材大多是狭长矩形或者曲边狭长矩形组成的开口薄壁杆件。

根据薄膜比拟，横截面的切应力方向是与狭长矩形的长边一致，而且数值不变。

这个条件使得狭长矩形的扭转切应力公式不难推导，同时，直边与曲边狭长矩形的应力分布是相同的。

对于开口薄壁杆件的扭转切应力分析，首先将开口薄壁杆件分解为一系列的狭长矩形。

这些狭长矩形共同承担截面内力扭矩，并且在扭矩作用下变形。

注意到各个狭长矩形的扭矩之和为外力矩，而相对扭矩角是相同的，可以得到各个狭长矩形的扭转切应力。

开口薄壁杆件的扭转切应力是在理想狭长矩形杆切应力基础上推导的，这个应力不能用于局部应力分析。

原因是开口薄壁杆件扭转切应力公式不能反映应力集中；而且为了减少应力集中的影响，工程型材在矩形与矩形的交接处有圆弧。

对于工程问题，局部应力分析可以查阅相关图表。

学习要点：
1. 狭长矩形的扭转应力；
2. 开口薄壁杆；
3. 开口薄壁杆扭转应力；
4. 局部切应力。

首先讨论狭长矩形的扭转应力，设狭长矩形的长边为a，短边长度为δ，而且a>>δ ，如图所示。

根据薄膜比拟，狭长矩形薄膜的形状沿长边方向基本不变，主要薄膜形状改变在短边方向。

因此可以推断，应力函数在横截面的几乎是不随长度方向变化，因此对应的薄膜形状近似于柱面。

所以可以近似地取
因此狭长矩形杆的扭转变形协调方程可以写作。

这是一个常微分方程，对上式作积分，并注意到边界条件，可得
将上述应力函数代入扭转端面边界条件，可得。

根据公式，有
最大切应力由薄膜比拟可以推论在矩形截面的长边上，其数值为。

单位长度的扭转角为。

上述结论与矩形截面杆件扭转应力分析结果完全一致。

工程结构中经常使用的开口薄壁杆，它们的横截面大都是由等宽度的狭长矩形组成的。

根据薄膜比拟可以想象，假如一个直边狭长矩形和一个曲边狭长矩形，它们具有相同的长度a和宽度δ，如果张在这两个狭长矩形上的薄膜受有相同的压力q和张力T，两个薄膜就与各自边界平面所占的体积V，以及薄膜的斜率大体是相同的。

因此,曲边狭长矩形截面扭杆与直边狭长矩形截面扭杆的扭转切应力是近似的。

所以，以下关于狭长矩形截面扭杆分析同样适用于曲边狭长矩形截面杆件。

如果用a i和δi分别表示开口薄壁杆第i个狭长矩形的长度和宽度，T i表示该矩形面积上承受的扭矩，τi表示该矩形长边中点的切应力，ϕ 为单位长度的扭转角。

则
根据合力条件，开口薄壁杆横截面的扭矩为
根据上述公式，消去ϕ，有。

回代可得
对于狭长矩形长边中点的切应力，上述公式给出了相当精确的解答。

但是需要注意的是：在开口薄壁杆件两个狭长矩形的连接处，由于应力集中，可能发生远大于狭长矩形中点的局部切应力。

开口薄壁杆件的局部应力与比值τmax/τi和ρ/δi有关，如图所示。

τmax是圆角处的最大切应力，τi是用公式计算出的切应力，ρ 是内圆角的曲率半径，δi 是狭长矩形的宽度。

图中列出局部应力与比值ρ/δi的关系。