2019届九年级数学下册课时同步练习题32

专题三开放型探索专题的青睐，中考题型以填空题、解答题为【课堂精讲】例1如图，在四边形ABCD中，点H是BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连结BE，CF．（1）请你添加一个条件，使得△BEH≌△CFH，你添加的条件是，并证明．（2）在问题（1）中，当BH与EH满足什么关系时，四边形BFCE是矩形，请说明理由．分析：（1）根据全等三角形的判定方法，可得出当EH=FH，BE∥CF，∠EBH=∠FCH时，都可以证明△BEH≌△CFH，（2）由（1）可得出四边形BFCE是平行四边形，再根据对角线相等的平行四边形为矩形可得出BH=EH时，四边形BFCE是矩形．解答：（1）添加：EH=FH，证明：∵点H是BC的中点，∴BH=CH，在△△BEH和△CFH中，，∴△BEH≌△CFH（SAS）；（2）解：∵BH=CH，EH=FH，∴四边形BFCE是平行四边形（对角线互相平分的四边形为平行四边形），∵当BH=EH时，则BC=EF，∴平行四边形BFCE为矩形（对角线相等的平行四边形为矩形）．本题考查了全等三角形的判定和性质以及平行四边形的判定基础题，难度不大例2.如图2－1－3，边长为1的正方形ABCD 的对角线AC ，BD 相交于点O .有直角∠MPN ，使直角顶点P 与点O 重合，直角边PM ，PN 分别与OA ，OB 重合，然后逆时针旋转∠MPN ，旋转角为θ(0°＜θ＜90°)，PM ，PN 分别交AB ，BC 于E ，F 两点，连结EF 交OB 于点G ，则下列结论中正确的是____． ①EF ＝2OE ；②S四边形OEBF∶S正方形ABCD＝1∶4；③BE ＋BF ＝2OA ；④在旋转过程中，当△BEF 与△COF 的面积之和最大时，AE ＝34；⑤OG ·BD ＝AE 2＋CF 2.图2－1－3 第4题答图【解析】 ∵四边形ABCD 是正方形，∴OB ＝OC ，∠OBE ＝∠OCF ＝45°，∠BOC ＝90°，∴∠BOF ＋∠COF ＝90°，∵∠EOF ＝90°，∴∠BOF ＋∠BOE ＝90°，∴∠BOE ＝∠COF ，∴△BOE ≌△COF (ASA )，∴OE ＝OF ，BE ＝CF ，∴EF ＝2OE .故①正确；∵S 四边形OE BF ＝S △BOE ＋S △BOF ＝S △BOF ＋S △COF ＝S △BOC ＝14S 正方形ABCD ，∴S 四边形OEBF ∶S 正方形ABCD ＝1∶4.故②正确；∵BE ＋BF ＝BF ＋CF ＝BC ＝2OA .故③正确；如答图，过点O 作OH ⊥BC 交BC 于点H ，∵BC ＝1，∴OH ＝12BC ＝12，设AE ＝x ，则BE ＝CF＝1－x ，BF ＝x ，∴S △BEF ＋S △COF ＝12BE ·BF ＋12CF ·OH ＝12x (1－x )＋12(1－x )×12＝－12⎝ ⎛⎭⎪⎫x －142＋932，∵a ＝－12＜0，∴当x ＝14时，S △BEF ＋S △COF 最大，即在旋转过程中，当△BEF 与△COF 的面积之和最大时，AE ＝14.故④错误；∵∠EOG ＝∠BOE ，∠OEG ＝∠OBE ＝45°，∴△OEG ∽△OBE ，∴OE ∶OB ＝OG ∶OE ，∴OG ·OB ＝OE 2，∵OB ＝12BD ，OE ＝22EF ，∴OG ·BD ＝EF 2，∵在△BEF 中，EF 2＝BE 2＋BF 2，∴EF2＝AE 2＋CF 2，∴OG ·BD ＝AE 2＋CF 2.故⑤正确．故答案为①②③⑤.【课堂提升】1.如图，直线a、b被直线c所截，若满足，则a、b平行．2.写出一个运算结果是a6的算式．3.如图2－1－5，CD是经过∠BCA顶点C的一条直线，CA＝CB.E，F分别是直线CD上两点，且∠BEC＝∠CFA＝∠α.(1)若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图①，若∠BCA＝90°，∠α＝90°，则BE____CF；EF____|BE－AF|(选填“＞”“＜”或“＝”)；②如图②，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件____，使①中的两个结论仍然成立，并证明两个结论成立．(2)如图③，若直线CD经过∠BCA的外部，∠α＝∠BCA，请写出EF，BE，AF三条线段数量关系的合理猜想(不要求证明)．图2－1－54.如图2－1－6①，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.(1)求证：△BDF是等腰三角形；(2)如图②，过点D作DG∥BE，交BC于点G，连结FG交BD于点O.①判断四边形BFDG的形状，并说明理由；②若AB＝6，AD＝8，求FG的长．5.如图，正方形ABCD中，点E，F分别在边AB，BC上，AF=DE，AF和DE相交于点G，(1)观察图形，写出图中所有与∠AED相等的角。

2019年重庆第32中学九年级数学总复习综合练习卷一、填空题（每小题3分，共36分）1、若a ，b 都是实数，b ＝+﹣2，则a b 的值为 ；2、点(3,2)P 关于x 轴对称的点的坐标为 ；3、若1x ，2x 是方程210x x --=的两个根，则1212x x x x ++⋅= ；4、计算：|2|-= ；5、如图，⊙O 为△ABC 的外接圆，若140BOC ∠=︒，则A ∠= 度；6、函数y x 的取值范围为 ；7、某公司一名员工，月工资由1200元增加了10%后达到 元；8、一组数据3、5、x 、6、7的平均数为5，则中位数为 ；9、人数相等的甲、乙两班学生参加同一次数学测验，班级平均分与方差分别为：x 甲=80，x 乙=80，2S 甲=240，2S x 甲=180，则测验成绩较整齐的是 班；10、圆锥的底面半径是4，母线长为5，则圆锥的侧面积等于 ；11、用正三角形与正方形作平面镶嵌，则在它的每一个顶点周围有3个正三角形和 个正方形；12、如图是一组有规律的图案，第1个图案由6个基础图形组成，第2个图案由11个基础图形组成，…，第n （n 是正整数）个图案中由 个基础图形组成．（用含n 的代数式表示）二、选择题（每小题4分，共24分）每小题有四个答案，其中有且只有一个答案是正确的，请把正确答案的代号，写在题后的括号内，答对的得4分，答错、不答或答案超过一个的一律得0分。

1、下列说法正确的是( )A．过弦的中点的直径平分弦所对的两条弧B．弦的垂直平分线平分它所对的两条弧，但不一定过圆心C．过弦的中点的直径垂直于弦D．平分弦所对的两条弧的直径平分弦2、如图，AB是⊙O直径，若∠AOC＝140°，则∠D的度数是（）A．20° B．30°C．40° D．70°3、如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为，则图中阴影部分的面积为（）A. B. C. D.4、如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A=30°，给出下面3个结论：①AD=CD；②BD=BC；③AB=2BC，其中正确结论的个数是（）A ．3B ．2C ．1D ．05、如图，在△ABC 中，∠C=90°，AB=4，以C 点为圆心，2为半径作⊙C ，则AB 的中点O 与⊙C 的位置关系是（ ）A ．点O 在⊙C 外B ．点O 在⊙C 上 C ．点O 在⊙C 内D ．不能确定181个圆的外切正六边形，接着作上述外切正六边形的外接圆，再作上述外接圆的外切正六边形，……，则按以上规律作出的第8个圆的外切正六边形的边长为（ ）A 、 7；B 、 8 ；C 、7(2 ；D 、8()2； 三、解答题（共90分）19、（8分）计算：3101(1)()23--+；解：20、（8分）先化简下面的代数式，再求值：2()2()x y x x y +-+，其中x =2y =；解：21、（8分）用换元法解方程： 22222x x x x -+=-；解；22、（8分）如图，已知点A 、C 、B 、D 在同一直线上，AM CN =，BM DN =，M N ∠=∠。

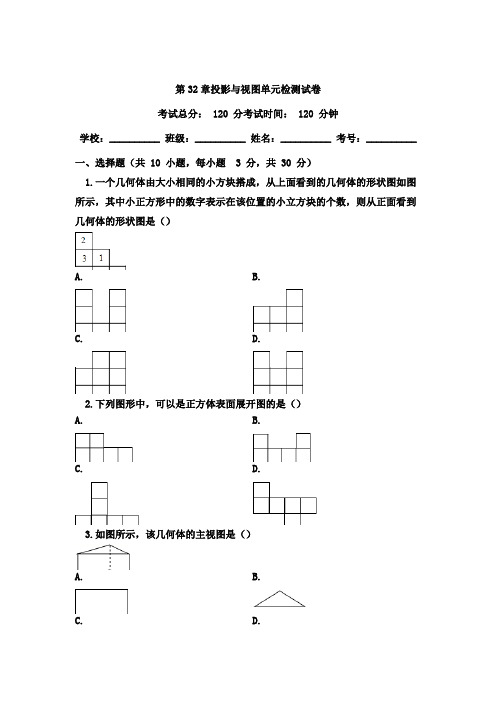
第32章投影与视图单元检测试卷 考试总分： 120 分考试时间： 120 分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________ 一、选择题（共 10 小题，每小题 3 分，共 30 分）1.一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是（）A.B.C.D.2.下列图形中，可以是正方体表面展开图的是（） A.B.C.D.3.如图所示，该几何体的主视图是（）A.B.C.D.4.如图是正方体的一个平面展开图，如果原正方体上“友”所在的面为前面，则“信”与“国”所在的面分别位于（）A.上，下B.右，后C.左，右D.左，后5.四个选项中四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体其中有三个几何体的某一种视图都是同一种几何图形，则另外一个几何体是（） A.B.C.D.6.用块完全相同的长方体搭成如图几何体，这个几何体从正面看到的形状是（）A.B.C.D.7.一个正方体盒子的每个面上都写有一个字，分别是：我、喜、欢、数、学、课，其平面展开图如图所示．那么在该正方体盒子中，与“我”相对的面上所写的字是（）A.欢B.数C.学D.课8.由相同的小立方体搭一个几何体，使得它的主视图和俯视图如图所示，搭成这种几何体至少需要（）个小立方体．A.B.C.D.9.如图是一个正方体被截去一角后得到的几何体，它的主视图是（）A.B.C.D.10.如图的四个平面图形中，不是正方体的展开图的是（） A.B.C.D.二、填空题（共 10 小题，每小题 3 分，共 30 分）11.为了测量操场中旗杆的高度，小明学习了“太阳光与影子”，设计了如图所示的测量方案，根据图中标示的数据可知旗杆的高度为________．12.一个长为 宽为 的矩形纸片以它的一边作为底面的周长，围成一个底面都是正方形的正四棱柱，则这个棱柱的体积是________．13.如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为________．14.身高相同的小明和小华站在灯光下的不同位置，如果小明离灯较远，那么小明的投影比小华的投影________．15.如图，它是一个正方体的展开图，若此正方体的相对面上的数互为相反数，则代数式________（填数值）．16.如图是同一时刻两根木杆的影子，则它们是________的光线形成的影子．17.如图，正方体的每个面上都写有一个实数，已知相对的两个面上的两数之和相等，若、、的对面的数分别是、、，则的值为________．18.如图是由五个大小相同小正方体堆成的立体图形，则该立体图形下面的视图的名称是________视图．（用“正”、“左”或“俯”填空）19.图中的立体图形由________个小正方体堆砌而成．20.桌上摆着一个由若干个相同正方体组成的几何体，从正面看和从左面看如图所示，这个几何体最多由________个这样的正方体组成．三、解答题（共 6 小题，每小题 10 分，共 60 分）21.已知，如图，和是直立在地面上的两根立柱，某一时刻在太阳光下的投影．请你在图中画出此时在太阳光下的投影；在测量的投影时，同时测量出在太阳光下的投影长为，请你计算的长．22.画出如图（由个相同的小正方体搭成的几何体）的主视图、左视图和俯视图．23.如图①是一些小正方体所搭几何体的俯视图，方格中的数字表示该位置的小正方体的个数．请在图②的方格纸中分别画出这个几何体的主视图和左视图．（要求涂上阴影）24.如图是几个正方体所组成的几何体的俯视图，小正方形中的数字表示该位置小正方块的个数．请画出这个几何体的主视图和俯视图．25.如图是由个相同的小立方块所搭几何体从上面看到的平面图形，小正方形中的数字表示在该位置小立方块的个数．请画出从正面、左面看这个几何体得到的平面图形．26.如图是两个正方体纸盒的表面展开图，请在空白的正方形内分别填入适当的数，使得折成正方体后相对面上的两个数互为相反数．答案1.D2.D3.D4.C5.C6.C7.C8.B9.B10.D11.12.或13.14.长15.16.点光源17.18.俯19.20.21.解：（连接，过点作，交直线于点，线段即为的投影，如图；∵，∴．∵，∴，∴，即∴．22.解：如图所示：23.解：由分析作图如下：24.解：如图所示主视图和左视图：25.解：如图所示：26.解：如图所示：。

2019年重庆第32中学九年级数学总复习综合练习卷一、填空题（每小题3分，共36分）1、若a ，b 都是实数，b ＝+﹣2，则a b 的值为 ；2、点(3,2)P 关于x 轴对称的点的坐标为 ；3、若1x ，2x 是方程210x x --=的两个根，则1212x x x x ++⋅= ；4、计算：|2|-= ；5、如图，⊙O 为△ABC 的外接圆，若140BOC ∠=︒，则A ∠= 度；6、函数y =x 的取值范围为 ；7、某公司一名员工，月工资由1200元增加了10%后达到 元；8、一组数据3、5、x 、6、7的平均数为5，则中位数为 ；9、人数相等的甲、乙两班学生参加同一次数学测验，班级平均分与方差分别为：x 甲=80，x 乙=80，2S 甲=240，2S x 甲=180，则测验成绩较整齐的是 班；10、圆锥的底面半径是4，母线长为5，则圆锥的侧面积等于 ；11、用正三角形与正方形作平面镶嵌，则在它的每一个顶点周围有3个正三角形和 个正方形；12、如图是一组有规律的图案，第1个图案由6个基础图形组成，第2个图案由11个基础图形组成，…，第n （n 是正整数）个图案中由 个基础图形组成．（用含n 的代数式表示）二、选择题（每小题4分，共24分）每小题有四个答案，其中有且只有一个答案是正确的，请把正确答案的代号，写在题后的括号内，答对的得4分，答错、不答或答案超过一个的一律得0分。

13、气温是零下4摄氏度，应记作（ ）A 、-4；B 、 4；C 、 -︒4C ；D 、︒4C14、计算32()x -的结果应是（ ）A 、5x ；B 、6x ；C 、5x -；D 、6x -； 15、不等式组{2312x x x <+<的解集是（ ）A 、32x < ；B 、1x > ；C 、 1332x << ；D 、312x << ； 16、如果一个角的补角是120︒，那么这个角的余角为（ ）A 、30︒ ；B 、60︒ ；C 、90︒ ；D 、150︒ ；17、过点(2,3)的正比例函数解析式是（ ）A 、23y x = ；B 、6y x = ；C 、21y x =- ；D 、32y x = ；181个圆的外切正六边形，接着作上述外切正六边形的外接圆，再作上述外接圆的外切正六边形，……，则按以上规律作出的第8个圆的外切正六边形的边长为（ ）A 、 7；B 、 8 ；C 、7 ；D 、8 ； 三、解答题（共90分）19、（8分）计算：3101(1)()23--+；解：20、（8分）先化简下面的代数式，再求值：2()2()x y x x y +-+，其中x =2y =；解：21、（8分）用换元法解方程： 22222x x x x -+=-； 解；22、（8分）如图，已知点A 、C 、B 、D 在同一直线上，AM CN =，BM DN =，M N ∠=∠。

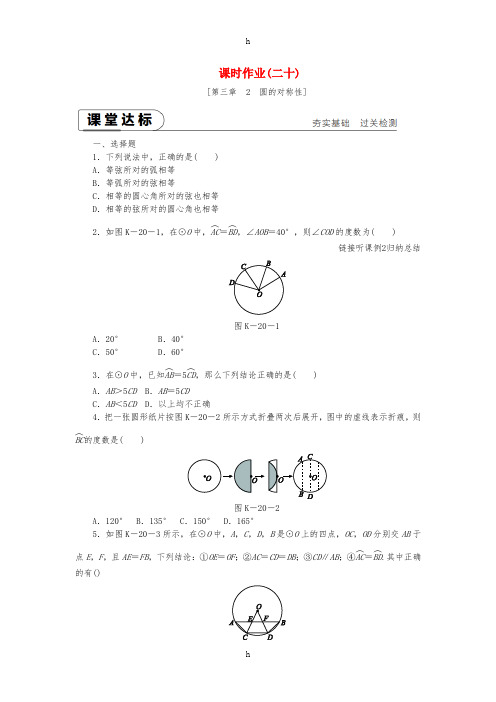
课时作业(二十)[第三章 2 圆的对称性]一、选择题1．下列说法中，正确的是( ) A ．等弦所对的弧相等 B ．等弧所对的弦相等C ．相等的圆心角所对的弦也相等D ．相等的弦所对的圆心角也相等2．如图K －20－1，在⊙O 中，AC ︵＝BD ︵，∠AOB ＝40°，则∠COD 的度数为( )链接听课例2归纳总结图K －20－1A ．20°B ．40°C ．50°D ．60°3．在⊙O 中，已知AB ︵＝5CD ︵，那么下列结论正确的是( )A ．AB ＞5CD B ．AB ＝5CDC ．AB ＜5CD D ．以上均不正确4．把一张圆形纸片按图K －20－2所示方式折叠两次后展开，图中的虚线表示折痕，则BC ︵的度数是( )图K －20－2A ．120°B ．135°C ．150°D ．165°5．如图K －20－3所示，在⊙O 中，A ，C ，D ，B 是⊙O 上的四点，OC ，OD 分别交AB 于点E ，F ，且AE ＝FB ，下列结论：①OE ＝OF ；②AC ＝CD ＝DB ；③CD ∥AB ；④AC ︵＝BD ︵.其中正确的有()A ．4个B ．3个C ．2个D ．1个 二、填空题6．如图K －20－4所示，在⊙O 中，若AB ︵＝CD ︵，则AB ＝______，∠AOB ＝∠______；若OE ⊥AB 于点E ，OF ⊥CD 于点F ，则OE ______OF .图K －20－47．如图K －20－5，在⊙O 中，AB ∥CD ，AC ︵所对的圆心角的度数为45°，则∠COD 的度数为________．图K －20－58．如图K －20－6，三圆同心于点O ，AB ＝4 cm ，CD ⊥AB 于点O ，则图中阴影部分的面积为________cm 2.图K －20－69．如图K －20－7，AD 是⊙O 的直径，且AD ＝6，点B ，C 在⊙O 上，AB ︵＝AC ︵，∠AOB ＝120°，E 是线段CD 的中点，则OE ＝________.链接听课例2归纳总结图K －20－710．如图K －20－8，AB 是⊙O 的直径，AB ＝10，BC ，CD ，DA 是⊙O 的弦，且BC ＝CD ＝DA ，若P 是直径AB 上的一动点，则PD ＋PC 的最小值为________．三、解答题11．xx·海淀区期中如图K －20－9，在⊙O 中，AB ︵＝CD ︵，求证：∠B ＝∠C .链接听课例2归纳总结图K －20－912．如图K －20－10所示，以平行四边形ABCD 的顶点A 为圆心，AB 的长为半径作圆，与AD ，BC 分别交于点E ，F ，延长BA 交⊙A 于点G .求证：GE ︵＝EF ︵.链接听课例3归纳总结图K －20－1013．如图K －20－11，AB 是⊙O 的直径，AC ︵＝CD ︵，∠COD ＝60°. (1)△AOC 是等边三角形吗？请说明理由； (2)求证：OC ∥BD .图K －20－1114．如图K －20－12，点A ，B ，C ，D ，E ，F 是⊙O 的六等分点． (1)连接AB ，AD ，AF ，求证：AB ＋AF ＝AD ；(2)若P 是圆周上异于已知六等分点的动点，连接PB ，PD ，PF ，写出这三条线段之间的数量关系(不必说明理由)．图K －20－1215．如图K －20－13，AB 是⊙O 的直径，C ，D 为圆上两点，且CB ︵＝CD ︵，∠CAE ＝∠CAB，CF ⊥AB 于点F ，CE ⊥AD 交AD 的延长线于点E. (1)试说明：DE ＝BF ；(2)若∠DAB ＝60°，AB ＝6，求△ACD 的面积．图K －20－13开放型问题如图K －20－14，⊙O 上有A ，B ，C ，D ，E 五点，且已知AB ＝BC ＝CD ＝DE ，AB ∥DE.(1)求∠BAE ，∠DEA 的度数；(2)连接CO 并延长交AE 于点G ，交AE ︵于点H ，写出三条与直径CH 有关的正确结论(不必证明)．图K －20－14详解详析【课时作业】 [课堂达标]1．[解析] B “在同圆或等圆中”是弧、弦、圆心角的关系定理成立的前提条件，不可忽视．以上选项中只有“等弧”满足该条件，所以B 正确．2．[解析] B ∵AC ︵＝BD ︵，∴AB ︵＝CD ︵，∴∠AOB ＝∠COD .∵∠AOB ＝40°，∴∠COD ＝40°.故选B.3．[解析] C ∵AB ︵＝5CD ︵，∴将弧AB 等分成5份，将每一个分点依次设为E ，F ，M ，N ，连接AE ，EF ，FM ，MN ，NB .∵5CD ＝AE ＋EF ＋FM ＋MN ＋NB ＞AB ，∴AB ＜5CD ，故选C.4．[解析] C 如图所示，连接BO ，过点O 作OE ⊥AB 于点E ，由题意可得EO ＝12BO ，AB ∥DC ，可得∠EBO ＝30°，故∠BOD ＝30°，则∠BOC ＝150°，故BC ︵的度数是150°.故选C.5．[解析] B ①③④正确． 6．[答案] CD COD ＝ 7．[答案] 90° 8．[答案] π[解析] AB ＝4 cm ，CO ⊥AB 于点O ，则OA ＝2 cm.根据圆的旋转不变性，把最小的圆逆时针旋转90°，把中间圆旋转180°，则阴影部分就合成了扇形OAC ，即圆面积的14，∴阴影部分的面积为14×π×(42)2＝π(cm 2)．9．[答案] 323[解析] ∵AB ︵＝AC ︵，∠AOB ＝120°，∴∠AOC ＝∠AOB ＝120°，∴∠DOC ＝60°.又∵OD ＝OC ，E 为DC 的中点，∴∠COE ＝12∠DOC ＝30°，OE ⊥DC .在Rt △OEC 中，cos30°＝OEOC.∵OC ＝12AD ＝12×6＝3，∴OE ＝323.10．[答案] 10[解析] 作点C 关于AB 的对称点C ′，连接OC ，OD ，OC ′，BC ′.∵BC ＝CD ＝DA ，∴∠AOD ＝∠COD ＝∠BOC ＝60°.∵点C 与点C ′关于AB 对称，∴BC ′＝BC ，∴∠BOC ′＝60°，∴D ，O ，C ′在同一条直线上，∴DC ′＝AB ＝10，即PD ＋PC 的最小值为10.11．证明：∵在⊙O 中，AB ︵＝CD ︵， ∴∠AOB ＝∠COD .又∵OA ＝OB ，OC ＝OD ，∴在△AOB 中，∠B ＝90°－12∠AOB ，在△COD 中，∠C ＝90°－12∠COD ，∴∠B ＝∠C .12．证明：连接AF .∵AB ＝AF ，∴∠ABF ＝∠AFB .∵四边形ABCD 是平行四边形，∴AD ∥BC ， ∴∠EAF ＝∠AFB ，∠GAE ＝∠ABF ， ∴∠GAE ＝∠EAF ，∴GE ︵＝EF ︵.13．[解析] (1)由等弧所对的圆心角相等推知∠1＝∠COD ＝60°；然后根据圆上的点到圆心的距离都等于圆的半径知OA ＝OC ，从而证得△AOC 是等边三角形；(2)通过证明同位角∠1＝∠B ，推知OC ∥BD .解：(1)△AOC 是等边三角形． 理由：如图，∵AC ︵＝CD ︵，∴∠1＝∠COD ＝60°.又∵OA ＝OC ，∴△AOC 是等边三角形． (2)证明：由(1)得∠1＝∠COD ＝60°， ∴∠BOD ＝60°.又∵OB ＝OD ，∴∠B ＝60°. ∴∠1＝∠B ，∴OC ∥BD .14．解：(1)证明：连接OB ，OF .∵点A ，B ，C ，D ，E ，F 是⊙O 的六等分点， ∴AD 是⊙O 的直径，且∠AOB ＝∠AOF ＝60°. 又∵OA ＝OB ，OA ＝OF ，∴△AOB ，△AOF 是等边三角形， ∴AB ＝AF ＝OA ＝OD ，∴AB ＋AF ＝AD . (2)当点P 在BF ︵上时，PB ＋PF ＝PD ； 当点P 在BD ︵上时，PB ＋PD ＝PF ； 当点P 在DF ︵上时，PD ＋PF ＝PB .15．解：(1)∵CB ︵＝CD ︵，∴CB ＝CD . 又∵∠CAE ＝∠CAB ，CF ⊥AB ，CE ⊥AD ， ∴CE ＝CF ，∴Rt △CED ≌Rt △CFB ，∴DE ＝BF .(2)连接OD ，OC .∵∠DAB ＝60°，OA ＝OD ， ∴△AOD 是等边三角形，∴AD ＝OA ＝OD ＝3，∠ADO ＝∠AOD ＝60°. ∵CB ︵＝CD ︵，∴∠COD ＝∠COB ＝60°.又∵OD ＝OC ，∴△COD 是等边三角形，∴CD ＝OD ＝3，∠ODC ＝60°，∴∠CDE ＝60°.在Rt △CDE 中，sin60°＝CE CD ，∴CE ＝3 32，∴S △ACD ＝12AD ·CE ＝12×3×3 32＝9 34.[素养提升]解：(1)连接BE ，AD ，∵AB ＝BC ＝CD ＝DE ， ∴AB ︵＝BC ︵＝CD ︵＝DE ︵， ∴BCE ︵＝ABD ︵，∴BE ＝AD .又∵AB ＝DE ，AE 是公共边，∴△ABE ≌△EDA ，∴∠BAE ＝∠DEA . 又∵AB ∥DE ，∴∠BAE ＋∠DEA ＝180°， ∴∠BAE ＝∠DEA ＝90°.(2)答案不唯一，如：①CH 平分∠BCD ；②CH ∥BA ；③CH ⊥AE . 欢迎您的下载，资料仅供参考！。

3．2 直棱柱、圆锥的侧面展开图基础题知识点1 直棱柱及其侧面展开图1．四棱柱的侧面展开图可能是(A)2．(2017·北京)如图是某个几何体的展开图，该几何体是(A)A.三棱柱B.圆锥C.四棱柱D.圆柱3．(教材P103练习T2变式)如图，直三棱柱的上下底面是直角三角形，请画出该直三棱柱的侧面展开图，并根据图中所标的数据求直三棱柱侧面展开图的面积.解：图略.AC＝32＋42＝5(cm)，它的侧面展开图的面积为2×4＋2×3＋2×5＝24(cm2).知识点2 圆锥及其侧面展开图4．下列图形中，是圆锥侧面展开图的是(B)5．用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，则这个圆锥的底面半径为(B) A.12B.1C.32D.26．(2018·宿迁)已知圆锥的底面圆半径为3 cm ，高为4 cm ，则圆锥的侧面积是15πcm 2.7．(教材P104习题T3变式)如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形.若圆锥底面圆的半径r ＝2 cm ，扇形的圆心角θ＝120°，则该圆锥的母线长l 为6cm.8．已知圆锥的侧面展开图是一个半径为12 cm ，弧长为12πcm 的扇形，求这个圆锥的侧面积及高. 解：侧面积为12×12×12π＝72π(cm 2).设底面半径为r ，则有2πr ＝12π，∴r ＝6 cm.由于高、母线、底面半径恰好构成直角三角形，根据勾股定理，可得圆锥的高为122－62＝63(cm). 中档题9．若圆锥的侧面展开图为半圆，则该圆锥的母线l 与底面半径r 的关系是(A) A.l ＝2r B.l ＝3rC.l ＝rD.l ＝32r10．(2018·绵阳)如图，蒙古包可近似看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为25πm 2，圆柱高为3 m ，圆锥高为2 m 的蒙古包，则需要毛毡的面积是(A) A.(30＋529)πm 2B.40πm 2C.(30＋521)πm 2D.55πm 211．如图，从直径为4 cm 的圆形纸片中，剪出一个圆心角为90°的扇形OAB ，且点A ，B 在圆周上，212．一个底面为正方形的直棱柱的侧面展开图是边长为12的正方形，则它的表面积为162. 13．将一个底面半径为6 cm ，母线长为15 cm 的圆锥形纸筒沿一条母线剪开并展平，求所得的侧面展开图的圆心角度数.解：由题意，得r ＝6 cm ，l ＝15 cm ，∴圆锥侧面积为S ＝πrl ＝π×6×15＝90π(cm2). ∴扇形面积为90π＝n π×152360，解得n ＝144.∴侧面展开图的圆心角度数是144°.14．已知一个直四棱柱的底面是边长为5 cm 的正方形，侧棱长都是8 cm ，回答下列问题： (1)将这个直四棱柱的侧面展开成一个平面图形，这个图形是什么形状？面积是多少？ (2)这个直四棱柱的体积是多少？解：(1)将这个直四棱柱的侧面展开成一个平面图形，这个图形是长方形，面积是4×5×8＝160(cm 2). (2)这个直四棱柱的体积是5×5×8＝200(cm 3). 综合题15．如图，正方体盒子的棱长为2，BC 的中点为M.(1)一只蚂蚁从点M 沿正方体的棱爬到点D 1，蚂蚁爬行的最短距离是多少？(2)若蚂蚁沿正方体的表面爬行到D 1点，你能画出表示蚂蚁爬行的最短路线并求出最短路线吗？ 解：(1)蚂蚁爬行的最短距离是MC ＋CC 1＋C 1D 1＝1＋2＋2＝5.(2)当把正方体的面B1BCC1展开到和面C1CDD1在同一平面上时，得到的图形如图所示. 图中线段MD1表示蚂蚁爬行的最短路线，最短路线是DD21＋MD2＝22＋32＝13.本文档仅供文库使用。

2.3 垂径定理基础题知识点 1 垂径定理1．(长沙中考改编)如图，在⊙Ｏ中，弦AB ＝6，圆心O 到AB 的距离OC ＝2，则⊙Ｏ的半径长为(B) A.72B.13C ．2 3D ．42．如图，AB 是⊙Ｏ的弦，OD ⊥AB 于D ，交⊙Ｏ于E ，则下列说法错误的是(D)A ．AD ＝BDB ．∠AOE ＝∠BOE C.AE ︵＝BE ︵ D ．OD ＝DE3．如图，在⊙Ｏ中，直径CD 垂直于弦AB.若∠C ＝25°，则∠BOD 的度数是(D) A ．25°B ．30°C ．40°D ．50°4．如图，AB 是⊙Ｏ的弦，半径OC ⊥AB 于点 D.若⊙Ｏ的半径为5，AB ＝8，则CD 的长是(A) A ．2B ．3C ．4D ．55．如图，AB 是⊙Ｏ的直径，弦CD ⊥AB 于点E ，OC ＝5 cm ，CD ＝6 cm ，则OE ＝4cm.6．(教材P59例1变式)如图，在⊙O中，直径AB垂直弦CD于点M，AM＝18，BM＝8，则CD的长为24．7．如图，AB是⊙Ｏ的直径，弦CD⊥AB于点E，点M在⊙Ｏ上，MD恰好经过圆心O，连接MB.若CD＝16，BE＝4，求⊙Ｏ的直径．解：∵AB⊥CD，CD＝16，∴CE＝DE＝8.设OB＝x，∵BE＝4，∴ｘ2＝(x－4)2＋82.解得x＝10.∴⊙Ｏ的直径是20.知识点 2 垂径定理的实际应用8．(教材P60习题T1变式)一条排水管的截面如图所示．已知排水管的截面圆半径OB＝10，截面圆圆心O到水面的距离OC是6，则水面宽AB是(A)A．16B．10C．8D．69．如图所示，某窗户是由矩形和弓形组成，已知弓形的跨度AB ＝3 m ，弓形的高EF ＝1 m ，现计划安装玻璃，请帮工程师求出AB ︵所在圆O 的半径r.解：由题意，知OA ＝OE ＝r.∵EF ＝1，∴OF ＝r －1. ∵OE ⊥AB ，∴AF ＝12AB ＝12×3＝1.5.在Rt △OAF 中，OF 2＋AF 2＝OA 2，即(r －1)2＋1.52＝r 2.解得r ＝138.∴圆O 的半径为138m.易错点忽略垂径定理的推论中的条件“不是直径”10．下列说法正确的是(D)A ．过弦的中点的直径平分弦所对的两条弧B ．弦的垂直平分线平分它所对的两条弧，但不一定过圆心C ．过弦的中点的直径垂直于弦D ．平分弦所对的两条弧的直径平分弦中档题11．如图，将半径为 2 cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为(C)A ．2 cmB.3 cmC ．2 3 cmD ．2 5 cm12．(2018·枣庄)如图，AB 是⊙Ｏ的直径，弦CD 交AB 于点P ，AP ＝2，BP ＝6，∠APC ＝30°.则CD 的长为(C) A.15B ．2 5C ．215D ．8提示：过点O 作OH ⊥PD 于H ，连接OD.AP ＝2，BP ＝6，则AO ＝BO ＝4，则PO ＝2，又∠OPH ＝∠APC ＝30°，∴OH ＝1，OD ＝OB ＝4，在Rt △HOD 中，HD ＝OD 2－OH 2＝15，∴CD ＝2HD ＝215.13．如图，以点P 为圆心的圆弧与x 轴交于A ，B 两点，点P 的坐标为(4，2)，点A 的坐标为(2，0)，则点B 的坐标为(6，0)．14．(2018·黄冈)如图，△ABC 内接于⊙O ，AB 为⊙Ｏ的直径，∠CAB ＝60°，弦AD 平分∠CAB.若AD ＝6，则AC ＝23．15．(2018·孝感)已知⊙Ｏ的半径为10 cm ，AB ，CD 是⊙Ｏ的两条弦，AB ∥CD ，AB ＝16 cm ，CD ＝12 cm ，则弦AB 和CD 之间的距离是2或14cm.16．(2018·安徽)如图，⊙Ｏ为锐角△ABC 的外接圆，半径为 5.(1)用尺规作图作出∠BAC 的平分线，并标出它与劣弧BC 的交点E ；(保留作图痕迹，不写作法)(2)若(1)中的点E 到弦BC 的距离为3，求弦CE 的长．解：(1)画图如图所示．(2)∵AE 平分∠BAC ，∴BE ︵＝EC ︵.连接OE ，OC ，EC ，则OE ⊥BC 于点F ，EF ＝3. 在Rt △OFC 中，由勾股定理可得，FC ＝OC 2－OF 2＝52－（5－3）2＝21.在Rt △EFC 中，由勾股定理可得，※精品试卷※CE＝FC2＋EF2＝21＋32＝30.17．如图，CD为⊙Ｏ的直径，弦AB交CD于点E，连接BD，OB.(1)求证：△AEC∽△DEB；(2)若CD⊥AB，AB＝8，DE＝2，求⊙Ｏ的半径．解：(1)证明：根据“同弧所对的圆周角相等”，得∠A＝∠D，∠C＝∠ABD，∴△AEC∽△DEB.(2)∵CD⊥AB，O为圆心，∴BE＝12AB＝4.设⊙Ｏ的半径为r，∵DE＝2，则OE＝r－2.∴在R t△OEB中，由勾股定理，得OE2＋EB2＝OB2，即(r－2)2＋42＝r2，解得r＝5.∴⊙Ｏ的半径为 5.综合题18．如图，已知∠MAN＝30°，O为边AN上一点，以O为圆心，2为半径作⊙O，交AN于D，E两点，设AD＝x.当x 为何值时，⊙Ｏ与AM相交于B，C两点，且∠BOC＝90°？解：过点O作OF⊥BC于点F.∵∠BOC＝90°，OB＝OC＝2，∴∠OBC＝45°，BC＝OB2＋OC2＝2 2.∵OF⊥BC，∴BF＝12BC＝2，∠BOF＝45°．∴∠OBF＝∠BOF.∴OF＝BF＝ 2.∵∠MAN＝30°，∴OA＝2OF＝2 2. ∴AD＝22－2，即当x＝22－2时，∠BOC＝90°．小专题(五) 与圆的基本性质有关的计算与证明1．已知：如图，A ，B ，C ，D 是⊙Ｏ上的点，∠1＝∠2，AC ＝3 cm. (1)求证：AC ︵＝BD ︵；(2)求BD 的长．解：(1)证明：∵∠1＝∠2，∴CD ︵＝AB ︵，∴CD ︵＋BC ︵＝AB ︵＋BC ︵. ∴AC ︵＝BD ︵. (2)∵AC ︵＝BD ︵，∴AC ＝BD. ∵AC ＝3 cm ，∴BD ＝3 cm.2．A ，B 是⊙Ｏ上的两个定点，P 是⊙Ｏ上的动点(P 不与A ，B 重合)，我们称∠APB 是⊙Ｏ上关于点A ，B 的滑动角．已知∠APB 是⊙Ｏ上关于点A ，B 的滑动角．(1)若AB 是⊙Ｏ的直径，则∠APB ＝90°；(2)如图，若⊙Ｏ的半径是1，AB ＝2，求∠APB 的度数．解：连接OA ，OB ，AB.∵⊙Ｏ的半径是1，即OA ＝OB ＝1，又∵AB ＝2，∴OA 2＋OB 2＝AB 2.※精品试卷※由勾股定理的逆定理可得，∠AOB＝90°．∴∠APB＝12∠AOB＝45°．3．如图，AB是⊙Ｏ的直径，C，D两点在⊙Ｏ上．若∠C＝45°．(1)求∠ABD的度数；(2)若∠CDB＝30°，BC＝3，求⊙Ｏ的半径．解：(1)连接AD.∵∠BCD＝45°，∴∠DAB＝∠BCD＝45°．∵AB是⊙Ｏ的直径，∴∠ADB＝90°．∴∠ABD＝45°．(2)连接AC.∵AB是⊙Ｏ的直径，∴∠ACB＝90°．∵∠CAB＝∠CDB＝30°，BC＝3，∴AB＝6.∴⊙Ｏ的半径为 3.4．如图，A，P，B，C是圆上的四个点，∠APC＝∠CPB＝60°，AP，CB的延长线相交于点 D.(1)求证：△ABC是等边三角形；(2)若∠PAC＝90°，AB＝23，求PD的长．※精品试卷※解：(1)证明：∵A，P，B，C是圆上的四个点，∴∠ABC＝∠APC，∠CPB＝∠BAC.∵∠APC＝∠CPB＝60°，∴∠ABC＝∠BAC＝60°．∴∠ACB＝60°．∴△ABC是等边三角形．(2)∵△ABC是等边三角形，∴∠ACB＝60°，AC＝AB＝BC＝2 3.∵∠PAC＝90°，∴∠DAB＝∠D＝30°．∴BD＝AB＝2 3.∵四边形APBC是圆内接四边形，∠PAC＝90°，∴∠PBC＝∠PBD＝90°．在Rt△PBD中，PD＝BDcos30°＝2332＝4.5．如图，一圆弧形桥拱的圆心为E，拱桥的水面跨度AB＝80米，桥拱到水面的最大高度为20米．求：(1)桥拱的半径；(2)现水面上涨后水面跨度为60米，求水面上涨的高度为多少米？解：(1)过点E作EF⊥AB于点F，延长EF交圆于点D，则由题意得DF＝20.由垂径定理知，点F是AB的中点，AF＝FB＝12AB＝40米，EF＝ED－FD＝AE－DF，由勾股定理知，AE2＝AF2＋EF2＝AF2＋(AE－DF)2. 设圆的半径是r，则r2＝402＋(r－20)2，解得r＝50.即桥拱的半径为50米．※精品试卷※(2)设水面上涨后水面跨度MN为60米，MN交ED于H，连接EM，则MH＝NH＝12MN＝30米，∴EH＝502－302＝40(米)．∵EF＝50－20＝30(米)，∴ＨF＝EH－EF＝10米．6．已知△ABC，以AB为直径的⊙Ｏ分别交AC，BC于点D，E，连接ED.若ED＝EC.(1)求证：AB＝AC；(2)若AB＝4，BC＝23，求CD的长．解：(1)证明：∵ED＝EC，∴∠EDC＝∠C.∵∠EDC＋∠ADE＝180°，∠ADE＋∠B＝180°，∴∠EDC＝∠B.∴∠B＝∠C.∴AB＝AC.(2)连接AE，∵AB为直径，∴AE⊥BC.由(1)知，AB＝AC，∴BE＝CE＝12BC＝ 3.在△ABC与△EDC中，∵∠C＝∠C，∠CDE＝∠B，∴△ABC∽△EDC.∴CECA＝CDCB.∴CE·CB＝CD·CA.∵AC＝AB＝4，∴3×２3＝4CD.∴CD＝3 2 .7．如图，在△ABC中，AB＝BC＝2，以AB为直径的⊙Ｏ分别交BC，AC于点D，E，且点D为BC的中点．(1)求证：△ABC为等边三角形；(2)求DE的长；(3)在线段AB的延长线上是否存在一点P，使△PBD≌△AED，若存在，请求出PB的长；若不存在，请说明理由．解：(1)证明：连接AD.∵AB是⊙Ｏ的直径，∴∠ADB＝90°．∵点D是BC的中点，∴AD是线段BC的垂直平分线．∴AB＝AC.∵AB＝BC，∴AB＝BC＝AC.∴△ABC为等边三角形．(2)连接BE.∵AB是直径，∴∠AEB＝90°．∴BE⊥AC.∵△ABC是等边三角形，∴AE＝EC，即E为AC的中点．∵Ｄ是BC的中点，故DE为△ABC的中位线，∴DE＝12AB＝12×2＝1.(3)存在点P使△PBD≌△AED，由(1)(2)知，BD＝ED，∵∠BAC＝60°，DE∥AB，∴∠AED＝120°．∵∠ABC＝60°，∴∠PBD＝120°．∴∠PBD＝∠AED.要使△PBD≌△AED，只需PB＝AE＝1.。

《锐角三角函数的计算》同步练习31．计算：(1)2 cos 230°－2 sin 60°·cos 45°；(2)2 sin30°－3 tan 45°＋4 cos 60°； (3);45tan 2160cos 30sin 45cos ︒+︒︒-︒ (4)︒-︒︒-+︒-︒45tan 60tan 45sin 22460tan 460tan 2． 2．填空： (1)在△ABC 中，∠C ＝90°，sin A ＝21，则 cos B ＝________； (2)已知α为锐角，且cos(90°－α)＝21，则α＝________； (3)若1)10(tan 3=︒+α，则锐角α＝________．3．选择题：(1)在△ABC 中，∠A ，∠B 都是锐角，且 sin A ＝21，cos B ＝22，则△ABC 三个角的大小关系是（ ）A ．∠C ＞∠A ＞∠B B ．∠B ＞∠C ＞∠AC ．∠A ＞∠B ＞∠CD ．∠C ＞∠B ＞∠A(2)若0°＜θ＜90°，且|sin 2θ－41|＋223cos ⎪⎪⎭⎫ ⎝⎛-θ，则tanθ的值等于（ ） A ．3 B ．33 C ．21 D ．23 4．已知α为锐角，当α-tan 11无意义时，求sin(α＋15°)＋cos (α－15°)的值． 5．等腰三角形的底边长为20，面积为33100上，求这个三角形各角的大小． 6．如图，∠C ＝90°，∠DBC ＝30°，AB ＝BD ，利用此图求tan 75°的值．7．如图，直升飞机在跨河大桥AB的上方点P处，此时飞机离地面的高度PO＝450 m，且A，B，O三点在一条直线上，测得∠α＝30°，∠β＝45°，求大桥AB的长(结果精确到0.01 m)．8．(1)比较sin 30°，sin 45°，sin 60°的大小及cos 30°，cos 45°，cos 60°的大小；(2)你能找出什么规律吗？参考答案1．(1)263-； (2) 0； (3) 212-； (4) 321-． 2．(1) 21； (2) 30°； (3) 20°． 3．(1) D ； (2) B ．4．3．5．30°，30°，120°．6．32+． 提示：设k CD 3=，BD ＝3k ． 7．桥长约 329.42 m ．8．(1) sin 30°＜sin 45°＜sin 60°，cos 60°＜cos 45°＜cos 30°；(2) 当 0°＜α＜90°时，sinα随α的增大而增大，cosα随α的增大而减小．初中数学试卷鼎尚图文**整理制作。

2019年课时同步练习（浙教版）九年级上3.2圆的轴对称性2【含答案及解析】姓名___________ 班级____________ 分数__________一、填空题1. 如图，AB是⊙O的弦，AB=8cm，⊙O的半径5cm，半径OC⊥AB于点D，则OD的长是cm．2. 如图，⊙O中，弦CD与直径AB相交于点E，∠AEC=45°，OF⊥CD，垂足为F，OF=2，DE=3，则DC= ．3. 已知⊙O中的弦AB长为12，弦心距为8，那么⊙O的半径为．4. 顶角为120°的等腰三角形的腰长为5cm，则它的外接圆的直径为．5. 如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM的取值范围是．6. 在半径为13的圆中，有两条长分别为10与24的弦互相平行，那么这两条平行弦之间的距离是．7. ⊙O的半径是20cm，弦AB∥弦CD，AB与CD间距离为4cm，若AB=24cm，则CD= cm．8. 如图，在平面直角坐标系中，⊙M与y轴相切于原点O，平行于x轴的直线交⊙M于P，Q两点，点P在点Q的右方，若点P的坐标是（﹣1，2），有下列结论：①点Q的坐标是（﹣4，2）；②PQ=3；③△MPQ的面积是3；④M点的坐标是（﹣3，0）．其中正确的结论序号是．（多填或错填的得0分，少填的酌情给分）9. （2013•宝应县二模）如图，在梯形ABCD中，AB∥DC，AB⊥BC，AB=2cm，CD=4cm．以BC上一点O为圆心的圆经过A、D两点，且∠AOD=90°，则圆心O到弦AD的距离是cm．10. 圆的半径为13cm，两弦AB∥CD，AB=24cm，CD=10cm，则两弦AB，CD的距离是．11. （2012•沙湾区模拟）在半径为1的⊙O中，弦AB、AC分别是、，则∠BAC的度数为．12. ⊙O的半径为7cm，⊙O内有一点P，OP=5cm，则经过P点所有弦中，弦长为整数的有条．13. 如图，AB是⊙O的弦，AB=10，⊙O的半径OC⊥AB于D，如果OD：DC=3：2，那么⊙O的直径长为．14. 如图，⊙O的弦AB⊥AC，AB=AC，OM⊥AB，ON⊥AC，垂足分别为M、N，若AB=2，则⊙O的半径为．15. 如图所示，AB为⊙0的直径，CD是弦，AB⊥CD于E点，若CD=8，则CE= ．16. 在平面直角坐标系中若一个圆分别与x轴、y轴相交于点（﹣2，0），（﹣4，0），（0，﹣1），则这个圆与y轴的另一个交点坐标是．17. 如图是一条直径为2米的圆形污水管道横截面，其水面宽1.6米，则此时污水的最大深度为米．18. 如图，⊙P与两坐标轴分别交于点A（﹣2、0）、B（﹣6、0）、C（0、﹣3）和点D，双曲线过点P，则k= ．19. 如图，⊙O的直径CD垂直于弦AB，垂足为点P，若AP=6cm，PD=4cm，则⊙O的直径为cm．20. 如图，正方形网格在平面直角坐标系中，△ABC顶点C的坐标是（7，4），则△ABC 外接圆的圆心坐标是．二、解答题21. 如图，AB交⊙O于M，N，且AM=BN，那么OA=OB吗？为什么？22. 如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD、BC，AB=5，AC=4，求：BD的长．23. 如图，A为圆O上半圆上的一个三等分点，B是AM的中点，P为直径MN上的一动点，圆O的半径为1，求AP+BP的最小值．24. 有一批圆心角为90°，半径为1的扇形状下脚料，现利用这批材料截取尽可能大的正方形材料，如图有两种截取方法：方法1，如图（1）所示，正方形OPQR的顶点P、Q、R 均在扇形边界上；方法2，如图（2）所示，正方形顶点C、D、E、F均在扇形边界上．图（1）、图（2）均为轴对称图形．试分别求这两种截取方法得到的正方形面积．并说明哪种截取方法得到的正方形面积更大？25. （2010•淮北模拟）有一座圆弧形的拱桥，桥下水面宽度8m，拱顶高出水面2m．现有一货船载一货箱欲从桥下经过，已知货箱宽6m，高1.5m（货箱底与水面持平），问该货船能否顺利通过该桥？26. 如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且AB=26m，OE⊥CD于点E．水位正常时测得OE：CD=5：24（1）求CD的长；（2）现汛期来临，水面要以每小时4m的速度上升，则经过多长时间桥洞会刚刚被灌满？27. 如图，P是⊙O外一点，PAB、PCD分别与⊙O分别交于A、B、C、D四点．PO平分∠BPD；求证：AB=CD．28. 如图所示，已知B、C两个乡镇相距25千米，有一个自然保护区A与B相距15千米，与C相距20千米，以点A为圆心，10千米为半径是自然保护区的范围，现在要在B、C两个乡镇之间修一条笔直的公路，请问：这条公路是否会穿过自然保护区？试通过计算加以说明．29. 如图，⊙O的半径为17cm，弦AB=30cm．（1）求圆心O到弦AB的距离；（2）若⊙O中另有一条CD=16cm，且CD∥AB，求AB和CD间的距离．30. 已知：如图，M是弧AB的中点，过点M的弦MN交弦AB于点C，设⊙O的半径为4cm，MN=4cm．（1）求圆心O到弦MN的距离；（2）猜想OM和AB的位置关系，并说明理由；（3）求∠ACM的度数．参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第27题【答案】第28题【答案】第29题【答案】第30题【答案】。

2019年精选初中九年级下册数学3.2 简单几何体的三视图浙教版课后辅导练习[含答案解析]五十九第1题【单选题】如图是3个相同的小正方体组合而成的几何体，它的俯视图是( )A、B、C、D、【答案】：【解析】：第2题【单选题】由五个同样大小的立方体组成如图的几何体，则关于此几何体三种视图叙述正确的是( )A、左视图与俯视图相同B、左视图与主视图相同C、主视图与俯视图相同D、三种视图都相同【答案】：【解析】：第3题【单选题】如图，由两个相同的正方体和一个圆锥体组成一个立体图形，其俯视图是( ) A、B、C、D、【答案】：【解析】：第4题【单选题】如图是由我市某中学楼层间的两个台阶组成的几何体，已知两个台阶的高度和宽度是相同的，据此可判断此几何体的三视图是( )A、B、C、D、【答案】：【解析】：第5题【单选题】如图1，把正方体沿上下底面的正方形对角线竖直方向切掉一半后得到图2，把切面作为正面观察，设它的主视图、左视图的面积分别为S1、S2 ，则S1：S2=( )A、1：2B、2：1C、有误：1D、2有误：1【答案】：【解析】：第6题【单选题】如图，该几何体的俯视图是( )A、B、C、D、【答案】：【解析】：第7题【单选题】过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示，它的俯视图为A、B、C、D、【答案】：【解析】：第8题【填空题】任意放置以下几何体：正方体、圆柱、圆锥、球体，则三视图都完全相同的几何体是______．【答案】：【解析】：第9题【填空题】在画三视图时，主、俯视图要______，主、左视图要______，左、俯视图要______．A、长对正B、高平齐C、宽相等【答案】：【解析】：第10题【作图题】如图是一个正方体被截去一个直三棱柱得到的几何体，请画出该几何体的三视图．A、解：如图所示：【答案】：【解析】：第11题【作图题】如图是用几个小正方体搭成的几何体，画出它的三视图。