【六年级数学】2018年六年级上册数学组合图形的周长和面积训练题(新人教版)

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

六年级数学计算组合图形面积练习题
班级考号姓名总分
1、求下列各图阴影部分的面积（单位：厘米）
2、计算下面图形的面积。

（单位：厘米）
3、计算下面图形中涂色部分的面积。

（单位：厘米）
4、求下面图形中涂色部分的面积。

（单位：厘米）
5、如下图示，AB＝4厘米，求涂色部分的面积。

6、计算下图中涂色部分的面积。

（6分）
7、如下图，正方形的面积是2平方分米，求圆的面积。

8、下面两个圆中直角等腰三角形的面积都是5平方厘米，求圆的面积。

9. 计算下图中阴影部分的面积．
10. 求阴影部分的面积．图中圆与长方形面积相等，长方形长6.28米。

阴影部分面积多少平方米？。

1.求阴影部分的面积。

(单位:厘米)
解：答案
2.求阴影部分的面积。

(单位:厘米)
解：答案
3.求阴影部分的面积。

(单位:厘米)
解：答案
4.求阴影部分的面积。

(单位:厘米)
解：答案
5.求阴影部分的面积。

(单位:厘米)
解：答案
6.求阴影部分的面积。

(单位:厘米)
解：答案
7.求阴影部分的面积。

(单位:厘米)
解：答案
8.求阴影部分的面积。

(单位:厘米)
解：答案
9.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

解：答案
10.正方形边长为2厘米，求阴影部分的面积。

解：答案
11.求阴影部分的面积。

(单位:厘米）
解：答案。

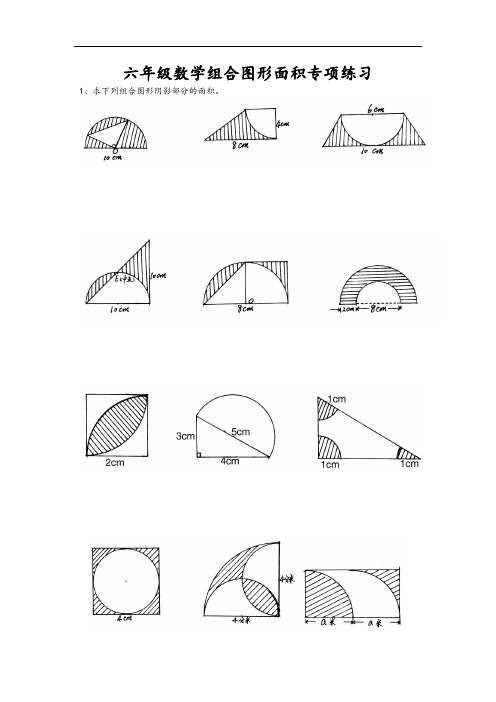
六年级数学组合图形面积专项练习1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

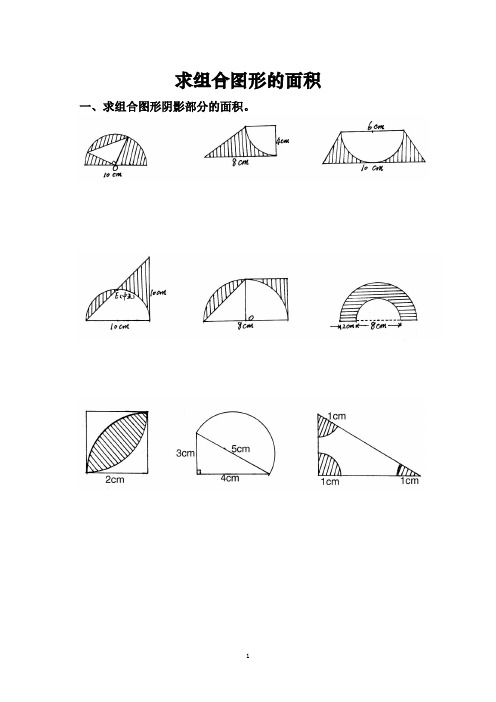
求组合图形的面积一、求组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

组合图形的周长练习题组合图形的周长练习题在数学学科中，几何形状是一个非常重要的概念。

而组合图形则是由多个简单的几何形状组合而成的复杂图形。

对于学生来说，理解和计算组合图形的周长是一个很好的练习，可以帮助他们巩固对几何形状的认识和计算能力。

本文将为你提供一些有趣的组合图形周长练习题。

问题一：矩形与半圆的组合假设有一个矩形，它的长为8cm，宽为4cm。

在矩形的一个边上，我们放置一个半径为2cm的半圆，使得半圆的直径与矩形的一条边相等。

请计算这个组合图形的周长。

解答：首先，我们需要计算矩形的周长。

矩形的周长可以通过将矩形的长和宽相加后乘以2来得到。

所以，这个矩形的周长为(8+4)cm * 2 = 24cm。

接下来，我们需要计算半圆的周长。

半圆的周长可以通过将半圆的直径乘以π（圆周率）来得到。

这个半圆的直径为2cm，所以半圆的周长为2cm * π。

最后，我们将矩形的周长和半圆的周长相加，得到这个组合图形的周长。

即24cm + 2cm * π ≈ 30.28cm。

问题二：正方形与等边三角形的组合现在，我们考虑一个由正方形和等边三角形组成的组合图形。

假设正方形的边长为6cm，而等边三角形的边长也为6cm。

请计算这个组合图形的周长。

解答：首先，我们需要计算正方形的周长。

正方形的周长可以通过将正方形的边长乘以4来得到。

所以，这个正方形的周长为6cm * 4 = 24cm。

接下来，我们需要计算等边三角形的周长。

等边三角形的周长可以通过将等边三角形的边长乘以3来得到。

所以，这个等边三角形的周长为6cm * 3 = 18cm。

最后，我们将正方形的周长和等边三角形的周长相加，得到这个组合图形的周长。

即24cm + 18cm = 42cm。

问题三：圆与矩形的组合在这个问题中，我们考虑一个由圆和矩形组成的组合图形。

假设圆的半径为5cm，而矩形的长为8cm，宽为6cm。

请计算这个组合图形的周长。

解答：首先，我们需要计算圆的周长。

六年级上册练习题组合图形练习题一：组合图形相关知识小结在六年级的数学学习中，组合图形是一个重要的内容。

组合图形是由两个或多个基本图形组合而成的复合图形。

通过将基本图形拼接、重叠、旋转等操作，可以形成多种不同的组合图形。

在解决组合图形问题时，需要运用图形的性质、相似性、对称性等概念和方法。

练习题二：拼凑组合图形小明拿到一些拼图，每个拼图都是由三个形状相同的小正方形组成。

他想利用这些拼图拼出一个面积为12平方厘米的大正方形。

请你帮助小明完成这个任务。

解题思路：首先，我们需要确定使用的基本图形为小正方形。

为了得到面积为12平方厘米的大正方形，我们可以将9个小正方形按照正方形的方式进行拼接。

拼接思路：首先，将3个小正方形横向排列，形成一行。

然后，再将这一行复制两次，依次垂直排列。

最后，将3行小正方形横向拼接成一个大正方形。

练习题三：拼图排列方案验证小明将9个小正方形按照我们的拼接思路完成了组合图形。

现在，我们来验证一下这个排列方案是否可以组成一个面积为12平方厘米的大正方形。

解题过程：首先，我们计算一下小正方形的边长。

由于小正方形面积为1平方厘米，所以它的边长为1厘米。

然后，我们计算一下大正方形的边长。

由于大正方形的面积为12平方厘米，所以它的边长为√12 ≈ 3.46厘米。

由上述计算可知，小正方形的边长为1厘米，大正方形的边长为3.46厘米。

小正方形的边长乘以3等于大正方形的边长，所以我们可以得出结论：这个排列方案可以组成一个面积为12平方厘米的大正方形。

练习题四：进一步探究组合图形小明对组合图形产生了更多的兴趣，于是他决定进一步探究组合图形。

他将尝试不同形状和数量的基本图形进行组合，看看会得到什么有趣的图形。

解题思路：对于小明的探究，我们可以通过以下步骤进行解答：1. 确定不同形状的基本图形，如三角形、矩形等；2. 确定不同数量的基本图形，如2个、3个、4个等；3. 尝试不同的排列方案，观察组合图形的形态和性质。

第十三节 组合图形的面积【知识要点】1．实际学习中，我们所学到的不只是单一图形，而往往是由几个基本图形组合成的组合图形,它们的面积不能直接运用公式来计算,需要我们从整体上观察图形，用灵活、巧妙的方法解答这类较复杂的图形计算问题。

2．算组合图形的方法通常用分割法、割补法、添补法、平移法、旋转法、剪拼法，加辅助线法等方法，对图形进行恰当合理的变形，找出解题的途径，正确计算。

【典型例题】例1 求下图的面积。

（单位：分米）例2 求下图中阴影部分面积。

（单位：厘米）1540例3 下图是由一个正方形和一个长方形拼成，求阴影部分的面积。

（单位：厘米）例4 图中三角形ABC的面积是36平方厘米，AC长8cm，DE长3cm。

求阴影部分的面积。

（ADFC不是正方形）例5 图中正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

例6 如图，正方形的边长为4cm，求阴影部分的面积是多少？3* 例7 在一个直角三角形铁皮上剪下一块正方形，并使正方形面积尽可能大，正方形的面积是多少？ （提示：连接DB ）单位：厘米。

* 例8 如图一个直角三角形铁皮ABCD,剪下一个长方形BEDF ，已知CE=4厘米,AF=12厘米，求长方形的面积是多少？*** 例9 用面积为12、36、24、48的四张小长方形纸片拼成一个如图所示的大长方形。

问：图中阴影部分的面积是多少？B4 E【小试锋芒】1．求阴影部分的面积。

（单位：厘米）2．图中平行四边形面积是280平方厘米，求阴影部分的面积。

3．如图，大小两个正方形的边长分别是10厘米和8厘米，求阴影部分的面积？4．如图，三个正方形的边长分别是1cm，2cm和3cm。

求图中阴影部分的面积。

5．如图，已知四条线的长度和两个直角，求四边形ABCD 的面积。

（单位：分米）* 6．在一个直角三角形铁皮上剪下一块正方形，并使正方形面积尽可能大，正方形的面积是多少？（提示：连接DB）单位：厘米。

六年级上册数学周长的练习题周长是数学中的一个重要概念，可以用来计算一个图形的边长之和。

在六年级上册的数学教材中，有很多关于周长的练习题，通过这些练习题，学生们可以巩固对周长的理解和应用能力。

本文将给出一些六年级上册数学周长的练习题，帮助学生们更好地掌握这一知识点。

练习题一：一张方形纸片的边长为8厘米，请计算该方形的周长。

解答：方形的周长等于四条边的长度之和。

由题目可知，该方形的边长为8厘米，所以周长=8+8+8+8=32厘米。

练习题二：一个矩形花坛的长为5米，宽为3米，请计算该花坛的周长。

解答：矩形的周长等于两倍长加两倍宽。

由题目可知，该矩形花坛的长为5米，宽为3米，所以周长=2×（5+3）=16米。

练习题三：一个等边三角形的边长为6厘米，请计算该三角形的周长。

解答：等边三角形的周长等于三条边的长度之和。

由题目可知，该等边三角形的边长为6厘米，所以周长=6+6+6=18厘米。

练习题四：一个梯形的上底为4米，下底为8米，高为5米，请计算该梯形的周长。

解答：梯形的周长等于上底、下底、两条斜边的长度之和。

由题目可知，该梯形的上底为4米，下底为8米，高为5米。

根据勾股定理，可以求得斜边的长度为√（5^2 + （8-4）^2）=√34米，所以周长=4+8+2×√34≈23.4米。

练习题五：一个正方形的对角线长为10厘米，请计算该正方形的周长。

解答：正方形的对角线等于边长的√2倍。

由题目可知，该正方形的对角线长为10厘米，所以边长=10÷√2≈7.07厘米，周长=4×7.07≈28.28厘米。

通过以上的练习题，我们可以看到不同类型的图形对应的周长计算方法是不同的。

要准确计算周长，需要根据图形的特点选择合适的计算公式，然后进行计算。

希望同学们通过这些练习题的训练，能够更加熟练地计算各种图形的周长，提高数学运算的能力。

圆的组合图形的周长和面积练习
例1 求图中阴影部分的面积（单位：厘米）。

【思路导航】如图所示的特点，阴影部分的面积可以拼成14
圆的面积。

62×3.14×14
＝28.26（平方厘米） 答：阴影部分的面积是28.26平方厘米。

练习1
求下面各个图形中阴影部分的面积（单位：厘米）。

答案：阴影部分的面积为：6×6×12 ＝18平方厘米
答案：阴影部分的面积为：（6+8）*6/2＝28平方厘米
6 6
6
6
6 6 6
6 6 6
2
例2 求图中阴影部分的面积（单位：厘米）。

【思路导航】阴影部分通过翻折移动位置后，构成了一个新的图形（如图19－6所示），从图中可
以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。

3.14×42×14
－4×4÷2÷2＝8.56（平方厘米） 答：阴影部分的面积是8.56平方厘米。

练习2
计算下面图形中阴影部分的面积（单位：厘米）。

答案：1、阴影部分的面积为：（2+2）×2＝8平方厘米
2、阴影部分的面积为：4×4×12
＝8平方厘米
4。