(完整版)三年级数学组合图形面积

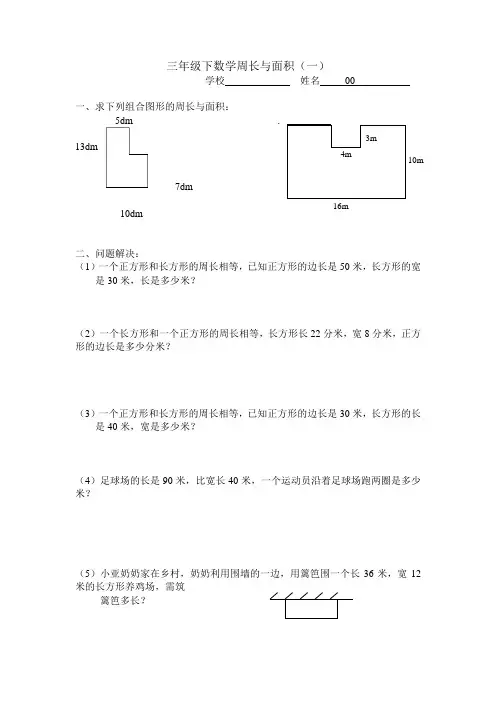
三年级下数学周长与面积（一） 学校 姓名 00一、求下列组合图形的周长与面积：5dm .13dm7dm10dm二、问题解决：（1）一个正方形和长方形的周长相等，已知正方形的边长是50米，长方形的宽是30米，长是多少米？（2）一个长方形和一个正方形的周长相等，长方形长22分米，宽8分米，正方形的边长是多少分米？（3）一个正方形和长方形的周长相等，已知正方形的边长是30米，长方形的长是40米，宽是多少米？（4）足球场的长是90米，比宽长40米，一个运动员沿着足球场跑两圈是多少米？（5）小亚奶奶家在乡村，奶奶利用围墙的一边，用篱笆围一个长36米，宽12米的长方形养鸡场，需筑篱笆多长？16m 4m 10m 3m（6）两个边长为3dm的正方形拼成一个长方形，这个长方形的周长是多少分米？（7）一个长方形的长是18厘米，宽是5厘米，如果长、宽各增加2厘米，面积增加多少？（8）把5个边长是3厘米的正方形，排成一个长方形，长方形的周长是多少？比正方形周长之和减少多少？（9）一个长方形的花坛长38dm，宽22dm，绕着这个花坛走两圈是多少m？如果一个人的步距约为3dm。

他绕花坛两圈共要走多少步？（10）会议室长10米，宽8米，用边长是4分米的地砖铺地，要用多少块？（11）这是小兔欢欢的家，中间是房间，周围是花园，房间是正方形，边长是8米。

A.25米B.在花园四周装上木栅栏，至少需要多少米长的木栅栏？（12）用24米长的篱笆围一个长方形的花坛，请你算一算，可以围成哪些面积？最大的面积是多少？三年级下数学周长与面积计算（二）1，计算下列图形的周长(单位：厘米)。

右上图是由边长为1厘米的11个正方形堆成的“土”字图形。

试求出其周长。

2，右图是某小学教学楼的平面示意图，设计者在图上只标明了三条线段的长度(单位：米)。

请你算出它的周长。

3，如右图所示，一个正方形被分成了三个相同的长方形。

如果其中一个长方形的周长是16米，那么这个正方形的周长是多少米？4，下面两图中的小方格的大小相同。

第二单元多边形的面积简单组合图形的面积教学内容：课本第21页。

教学目标：1、使学生结合生活实际认识组合图形，会把组合图形分解成学过的平面图形并计算出面积2、能运用所学知识解决生活中组合图形的实际问题。

3、自主探索，合作交流。

培养学生认真思考，团结协作的能力。

4、通过找一找、分一分、拼一拼,培养学生识图的能力和综合运用有关知识的能力,能合理地运用“割”、“补”等方法来计算组合图形的面积。

教学重点：探索并掌握组合图形的面积计算方法。

教学难点：理解并掌握组合图形的组合及分解方法。

教学准备：课件教学过程：一、创设情境,激趣导入。

1、同学们,我们已经学习了哪些多平面图形?导学要点：请同学们看大屏幕，认识组合图形。

像这样由几种简单图形组合而成的图形，我们就把它们叫做组合图形。

2、感知：组合图形在我们生活中的应用很广泛（生举例），今天，我们就结合一个生活中的例子来学习组合图形的面积。

板书：组合图形的面积二、小组合作探究1、出示前置性作业小组交流复习（1）说说你学过哪些平面图形？第二天我们找到了一个连家具出租的美丽小洋房，马上又挂长途电话去马德里。

长沙相亲 。

英语的单词是很重要的一项，英语想要拿到高分，就一定需要在英语单词上多下功夫，学好单词也是英语逆袭的必要条件，想要掌握好英语单词的话，最好不要大面积占用时间来背英语单词，可以将英语单词的学习时间分为一些零散的闲暇时间“父亲，我们的新地址是这个，你们记下来。

在海边，是，暂时住下来，不回西班牙。

是，请母亲不要担心。

这里风景很好，她可以来玩，先通知我们，就可以来。

是，大概二千多公里的距离，乔其姐夫知道在哪里，你们看看地图，好，知道了，好荷西在讲电话，我在一边用手指划灰灰的玻璃，静静的听着。

等荷西挂上电话推门出来了，我才不划了，预备跟他走。

“唉，三毛，你在玻璃上写了那么多‘钱’字做什么？”荷西瞪着看我划的字，好新鲜的样子。

“中西的不同在此也。

嘿嘿！”我感喟的说了一句。

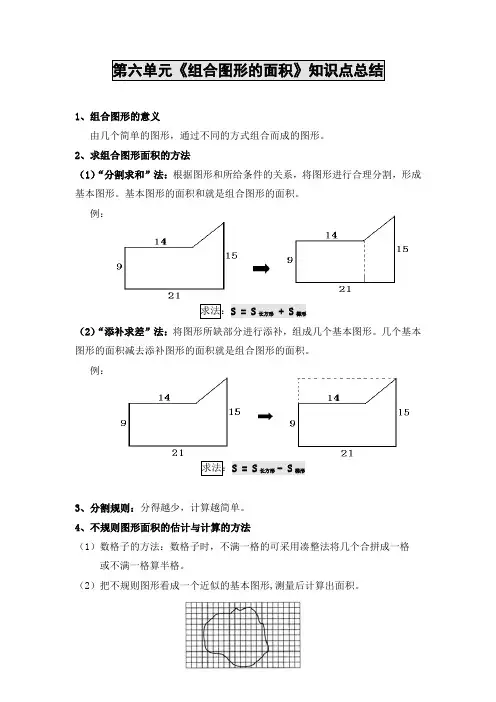
第六单元《组合图形的面积》知识点总结1、组合图形的意义由几个简单的图形，通过不同的方式组合而成的图形。

2、求组合图形面积的方法（1）“分割求和”法：根据图形和所给条件的关系，将图形进行合理分割，形成基本图形。

基本图形的面积和就是组合图形的面积。

例：求法：S = S长方形 + S梯形（2）“添补求差”法：将图形所缺部分进行添补，组成几个基本图形。

几个基本图形的面积减去添补图形的面积就是组合图形的面积。

例：求法：S = S长方形- S梯形3、分割规则：分得越少，计算越简单。

4、不规则图形面积的估计与计算的方法（1）数格子的方法：数格子时，不满一格的可采用凑整法将几个合拼成一格或不满一格算半格。

（2）把不规则图形看成一个近似的基本图形,测量后计算出面积。

5、常见基本图形的面积（1）长方形：周长＝(长+宽)×2字母公式：C=(a+b)×2面积＝长×宽字母公式：S＝ab（2）正方形：周长＝边长×4字母公式：C=4a面积＝边长×边长字母公式：S＝a2（3）平行四边形的面积＝底×高字母公式：S＝ah底=面积÷高；高=面积÷底（4）三角形的面积＝底×高÷2 字母公式：S＝ah÷2 底=面积×2÷高；高=面积×2÷底（5）梯形的面积＝(上底＋下底)×高÷2 字母公式：S＝(a＋b)×h÷2 上底=面积×2÷高－下底；下底=面积×2÷高－上底；高=面积×2÷（上底+下底）6、常用的单位间的进率（1）长度单位：千米（km）米（m）分米（dm）厘米（cm）毫米（mm）1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米（2）面积单位：平方千米（km2）公顷平方米（m2）平方分米（dm2）平方厘米（cm2）1平方千米=100公顷=1000000平方米 1公顷=10000平方米1平方米=100平方分米=10000平方厘米 1平方分米=100平方厘米（3）质量单位：吨（t）千克（kg）克（g）1吨=1000千克 1千克=1000克【注】单位换算的方法：大化小，乘进率；小化大，除以进率。

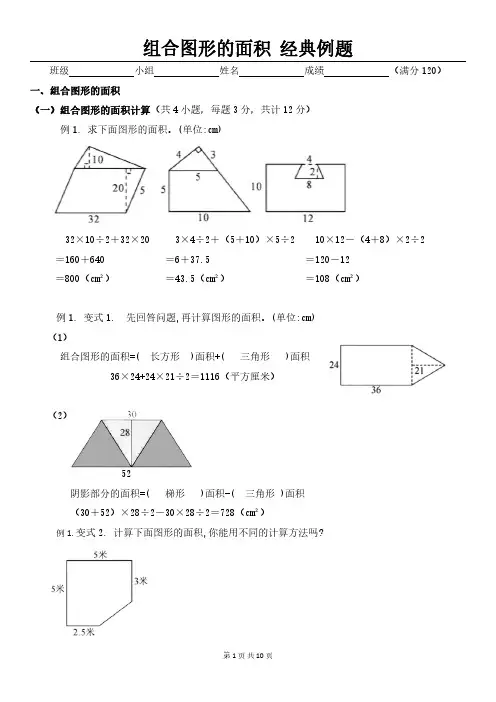
班级小组姓名成绩（满分120）一、组合图形的面积（一）组合图形的面积计算（共4小题，每题3分，共计12分）例1.求下面图形的面积。

(单位:cm)32×10÷2＋32×203×4÷2＋（5＋10）×5÷210×12－（4＋8）×2÷2＝160＋640＝6＋37.5＝120－12＝800（cm²）＝43.5（cm²）＝108（cm²）例1.变式1.先回答问题,再计算图形的面积。

(单位:cm)（1）组合图形的面积=(长方形)面积+(三角形)面积36×24+24×21÷2＝1116（平方厘米）（2）52阴影部分的面积=(梯形)面积-(三角形)面积（30＋52）×28÷2－30×28÷2＝728（cm²）例1.变式2.计算下面图形的面积,你能用不同的计算方法吗?5×2.5＋（3＋5）×（5－2.5）÷2＝5×2.5＋8×2.5÷2＝12.5＋10＝22.5（平方米）5×3＋（2.5＋5）×（5－3）÷2＝5×3＋7.5×2÷2＝15＋7.5＝22.5（平方米）例1.变式3.如图,左边阴影部分的面积是60平方厘米。

求右边空白部分(梯形)的面积。

(单位:厘米)60×2÷8＝15（厘米）（16＋16＋8）×15÷2＝40×15÷2＝300（平方厘米）答：空白部分的面积是300平方厘米.（二）组合图形的面积计算（共4小题，每题3分，共计12分）例2.计算下列组合图形的面积。

(单位:cm)（8.5＋15）×13÷2－8.5×4÷2＝135.75（cm²）例2.变式1.解决问题。

三年级数学组合图形面积1.右图是一幢楼房的平面图形,它的面积是 平方米.(单位:米)2.北京某四合院子正好是个边长10米的正方形,在院子中央修了一条宽2米的“十字形”甬路,如图.这条“十字形”甬路的面积是 平方米?3.右图中有四个正方形,图①的边长是32厘米,图②的边长是图①边长的一半;图③的边长是图②边长的一半;图④的边长是图③边长的一半.图中图①(最大的正方形)的面积是图④(最小的正方形)面积的 倍? 4.右图中有3个长方形,图①长32厘米,宽16厘米;图②的长、宽分别是图①长、宽的一半;图③的长、宽分别是图②长、宽的一半.图①的面积是图③面积的 倍?5.有大、小两个长方形,对应边的距离均为1厘米,如果两个长方形之间(阴影部分)部分的面积是16平方厘米,且小长方形的长是宽的2倍.求大长方形的面积是小长方形的 倍.7.一个长方形原来的长是12厘米,宽是7厘米.现在把长和宽都减少2厘米,那么面积减少了 平方厘米?8.把20分米长的线段分成两段,并在每一段上作一正方形(如下图).已知两个正方形的面积差为40平方分米,求每个正方形的面积.9.右图中有六个正方形,较小的正方形都由较大的正方形的四边中点连接而成.已知最大的正方形的面积为32cm 2,那么最小的正方形的面积等于 2cm .① ③ ②20分米拓展部分例1 把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米？练习. 把一张长6厘米，宽4厘米的长方形纸剪成一个面积最大的正方形，这张正方形纸的面积是多少平方厘米？例2 计算下面图形的面积。

（单位：厘米）(1)15203040(2)31122 (3)1112514例3 .有两个相同的长方形，长是8厘米，宽是3厘米。

如果把它们按下图叠放，这个图形的面积是多少？练习. 两张边长8厘米的正方形纸，一部分叠在一起放在桌上（如下图），桌面被盖住的面积是多少？8884483米4米一个长方形与一个正方形部分重合（如下图），求两个阴影部分面积相差多少？（单位：厘米）例4 .把一个长18厘米，宽6厘米的长方形纸，剪成边长3厘米的小正方形纸，问能剪成多少个这样的小正方形？练习. 把一个长20厘米，宽16厘米的长方形，分割成边长4厘米的小正方形，最多能分割成多少个小正方形？例5 一个长方形若长增加2厘米，面积就增加10平方厘米，若宽减少3厘米，面积就减少18平方厘米。

第二单元多边形的面积简单组合图形的面积教学内容：课本第21页。

教学目标：1、使学生结合生活实际认识组合图形，会把组合图形分解成学过的平面图形并计算出面积2、能运用所学知识解决生活中组合图形的实际问题。

3、自主探索，合作交流。

培养学生认真思考，团结协作的能力。

4、通过找一找、分一分、拼一拼,培养学生识图的能力和综合运用有关知识的能力,能合理地运用“割”、“补”等方法来计算组合图形的面积。

教学重点：探索并掌握组合图形的面积计算方法。

教学难点：理解并掌握组合图形的组合及分解方法。

教学准备：课件教学过程：一、创设情境,激趣导入。

1、同学们,我们已经学习了哪些多平面图形?导学要点：请同学们看大屏幕，认识组合图形。

像这样由几种简单图形组合而成的图形，我们就把它们叫做组合图形。

2、感知：组合图形在我们生活中的应用很广泛（生举例），今天，我们就结合一个生活中的例子来学习组合图形的面积。

板书：组合图形的面积二、小组合作探究1、出示前置性作业小组交流复习（1）说说你学过哪些平面图形？王安石变法的基本特征：他勇于进取，无所畏惧，又非常务实，提出较全面的政治改革思想，并全力实施，使北宋时期的改革思潮和实践达到顶峰。

在他执政期间进行了大刀阔斧的政治改革，内容涉及政治、经济、文化、军事等方面，影响巨大，对增强北宋的国力、巩固统治起了一定的作用。

电源旋转开关生产厂家https:///product-selection/rotary/ 。

英语的单词是很重要的一项，英语想要拿到高分，就一定需要在英语单词上多下功夫，学好单词也是英语逆袭的必要条件，想要掌握好英语单词的话，最好不要大面积占用时间来背英语单词，可以将英语单词的学习时间分为一些零散的闲暇时间他的改革精神是不朽的，是永远值得继承和发扬的。

现在中国改革开放就是对王安石改革精神的继承和发扬，改革四十年所取得的巨大成就，再一次充分证明改革是强国富民的神器。

二是他的文学成就，散文和诗词都创造了辉煌，成就了他在文学史上的地位。

第二单元多边形的面积简单组合图形的面积教学内容：课本第21页。

教学目标：1、使学生结合生活实际认识组合图形，会把组合图形分解成学过的平面图形并计算出面积2、能运用所学知识解决生活中组合图形的实际问题。

3、自主探索，合作交流。

培养学生认真思考，团结协作的能力。

4、通过找一找、分一分、拼一拼,培养学生识图的能力和综合运用有关知识的能力,能合理地运用“割”、“补”等方法来计算组合图形的面积。

教学重点：探索并掌握组合图形的面积计算方法。

教学难点：理解并掌握组合图形的组合及分解方法。

教学准备：课件教学过程：一、创设情境,激趣导入。

1、同学们,我们已经学习了哪些多平面图形?外汇跟单详细问题了解下！导学要点：请同学们看大屏幕，认识组合图形。

像这样由几种简单图形组合而成的图形，我们就把它们叫做组合图形。

2、感知：组合图形在我们生活中的应用很广泛（生举例），今天，我们就结合一个生活中的例子来学习组合图形的面积。

板书：组合图形的面积二、小组合作探究1、出示前置性作业小组交流复习（1）说说你学过哪些平面图形？（2）说说这些图形的面积计算公式？2、自学21页的例10（1）导学单1）小组合作将组合图形分成我们学习过的图形。

说说你的分法，你是怎样想的？2）尝试计算每个图形的面积。

3）思考：组合图形的面积是怎样计算出来的？导学要点：（1）分割法：将整体分成几个基本图形，求出它们的面积和。

（2）添补法：用一个大图形减去一个小图形求出组合图形的面积。

师:你是怎样想的?这两种解法你喜欢用哪一种解法?说说你的理由。

（2）小组交流1）从例题中我们可以看出,同一个组合图形，我们可以运用怎样的方法来解决？2）由于方法不同，我们计算组合图形的方法有什么不同？3）求组合图形面积时关键是做什么?导学要点：（1）要根据原来图形的特点进行思考。

（2）要便于利用已知条件计算简单图形的面积。

（3）可以用不同的方法进行割补。

（3）全班交流1）学生举例并解答（前置作业我的例子）2）结合学生自己举的例子解答讲解。