威布尔分布
- 格式:ppt
- 大小:4.13 MB
- 文档页数:121

威布尔分布参数计算方法\[ f(x;\lambda, k) = \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1} e^{-(x/\lambda)^k} \]其中,$\lambda>0$和$k>0$是威布尔分布的两个参数,$\lambda$称为尺度参数,$k$称为形状参数。
下面将介绍如何计算威布尔分布的参数。
##最大似然估计法最常用的参数估计方法是最大似然估计法。
假设我们有$n$个样本数据$x_1, x_2, ..., x_n$,要估计威布尔分布的参数$\lambda$和$k$。
首先,根据概率密度函数,我们可以得到似然函数:\[ L(\lambda, k ; x_1, x_2, ..., x_n) = \prod_{i=1}^{n}\frac{k}{\lambda} \left(\frac{x_i}{\lambda}\right)^{k-1} e^{-(x_i/\lambda)^k} \]为了方便计算,我们可以求似然函数的对数:\[ \log L(\lambda, k ; x_1, x_2, ..., x_n) = n \log k - n \log \lambda + (k-1) \sum_{i=1}^{n}\log\left(\frac{x_i}{\lambda}\right) - \sum_{i=1}^{n}\left(\frac{x_i}{\lambda}\right)^k \]接下来,我们需要最大化对数似然函数。
可以通过求偏导数等于0来求解最大化的参数。
求解$\lambda$的最大似然估计值:\[ \frac{\partial \log L}{\partial \lambda} = -\frac{n}{\lambda} + \frac{(k-1)}{\lambda} \sum_{i=1}^{n}\frac{x_i}{\lambda} - \sum_{i=1}^{n} \frac{x_i^k}{\lambda^{k+1}} = 0 \]化简上式得到:\[ \sum_{i=1}^{n} \left(\frac{x_i}{\lambda}\right)^k =\frac{(k-1)}{n} \sum_{i=1}^{n} \frac{x_i}{\lambda} \]我们可以定义一些中间变量:\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]\[ s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2} \]将上面的结果代入方程中:\[ \left(\frac{\bar{x}}{\lambda}\right)^k = \frac{(k-1)}{n} \frac{\bar{x}}{\lambda} \]进一步整理可得:\[ \lambda = \left(\frac{\bar{x}}{k-1}\right)^{1/k} \]接下来求解$k$的最大似然估计值,我们将$\lambda$的最大似然估计值带入似然函数中,得到:\[ \log L(k ; x_1, x_2, ..., x_n) = n \log k - n \log\left(\frac{\bar{x}}{k-1}\right)^{1/k} + (k-1) \sum_{i=1}^{n}\log\left(\frac{x_i}{\left(\frac{\bar{x}}{k-1}\right)^{1/k}}\right) - \sum_{i=1}^{n}\left(\frac{x_i}{\left(\frac{\bar{x}}{k-1}\right)^{1/k}}\right)^k \]类似地,对上式求偏导等于0,可以得到对$k$的求解。

Python威布尔分布曲线拟合1. 介绍威布尔分布是一种描述时间或寿命数据的统计分布,广泛应用于可靠性工程、医学、环境科学等领域。
在实际应用中,我们经常需要对数据进行威布尔分布的拟合,以了解数据的分布特征并进行进一步的分析。
2. 什么是威布尔分布威布尔分布是一种连续概率分布,其概率密度函数为:f(x;λ, k) = (k/λ) * (x/λ)^(k-1) * exp(-(x/λ)^k),其中x≥0,λ>0,k>0。
λ和k 分别为威布尔分布的尺度参数和形状参数,决定了分布的特征。
3. Python中的威布尔分布拟合在Python中,我们可以使用SciPy库中的stats模块来进行威布尔分布的拟合。
我们需要导入相应的库:```pythonimport numpy as npimport matplotlib.pyplot as pltfrom scipy import stats```4. 生成数据为了进行威布尔分布的拟合,我们首先需要准备一组数据。
假设我们有一组寿命数据,我们可以使用NumPy库生成符合威布尔分布的随机数据:```pythondata = np.random.weibull(k, size=1000)```5. 进行拟合有了数据之后,我们就可以使用stats模块中的weibull_min类来进行拟合:```pythonparams = stats.weibull_min.fit(data, loc=0)```6. 绘制拟合曲线我们可以利用拟合得到的参数来绘制威布尔分布的概率密度函数曲线:```pythonx = np.linspace(0, 5, 100)y = stats.weibull_min.pdf(x, *params)plt.plot(x, y, 'r-', lw=2)plt.hist(data, bins=30, density=True, alpha=0.6)plt.show()```7. 结论通过以上步骤,我们就可以在Python中实现对威布尔分布的数据拟合,并得到拟合曲线。

正态分布指分布对数正态分布和威布尔分布函数及其在工程分析中的应用正态分布是统计学中最常用的概率分布之一、如果一个随机变量X服从正态分布,记为X~N(μ,σ^2),其中μ是均值,σ^2是方差,那么X的概率密度函数为:f(x) = 1 / (σ * √(2π)) * exp(- (x-μ)^2 / (2σ^2))正态分布有很多特点和应用。
首先,正态分布是一个钟形曲线,对称分布,均值、中位数和众数都在一起。
均值决定了曲线的位置,方差决定了曲线的宽度。
正态分布的中心部分更为密集,离中心越远概率越小,而在3个标准差以内的区域包含了大约68%的样本。
正态分布在工程分析中有很多应用。
一方面,正态分布在统计过程控制和质量管理中经常使用。
例如,在生产过程中产品尺寸的变异可以用正态分布来描述,通过控制图可以监测和控制生产过程。
另一方面,正态分布在工程测量和可靠性分析中也有广泛应用。
测量误差和信号噪声常常被假设为服从正态分布,这样我们可以利用正态分布的特性来分析和处理测量数据。
此外,正态分布也经常用于风速、水位、降水量等自然现象的统计分析。
指数分布是一种连续概率分布,用于描述事件发生的时间间隔。
指数分布的随机变量X表示一个事件发生之间的时间间隔,参数λ表示单位时间内发生事件的平均次数。
指数分布的概率密度函数为:f(x) = λ * exp(- λx)指数分布在工程分析中常用于可靠性分析和故障率分析。
例如,设备的故障时间间隔(如无故障运行时间)可以用指数分布来描述,我们可以利用指数分布的特性来估计设备的可靠性参数。
此外,指数分布还常用于研究随机事件的等待时间,如顾客在银行排队等待的时间间隔。
对数正态分布是一种连续概率分布,其随机变量的对数服从正态分布。
如果随机变量X服从对数正态分布,记为X~LN(μ,σ^2),其中μ和σ^2为正态分布的均值和方差,那么X的概率密度函数为:f(x) = 1 / (x * σ * √(2π)) * exp(-[(ln(x)-μ)^2] /[2σ^2])对数正态分布常用于描述正数随机变量的分布,例如收入、房价等。

威布尔分布函数韦布尔分布,即韦伯分布(Weibull distribution),又称韦氏分布或威布尔分布,是可靠性分析和寿命检验的理论基础。
威布尔分布在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式。
由于它可以利用概率值很容易地推断出它的分布参数,被广泛应用于各种寿命试验的数据处理。
历史(History)1. 1927年,Fréchet(1927)首先给出这一分布的定义。
2. 1933年,Rosin和Rammler在研究碎末的分布时,第一次应用了韦伯分布(Rosin, P.; Rammler, E. (1933), "The Laws Governing the Fineness of Powdered Coal", Journal of the Institute of Fuel 7: 29 - 36.)。
3. 1951年,瑞典工程师、数学家Waloddi Weibull(1887-1979)详细解释了这一分布,于是,该分布便以他的名字命名为Weibull Distribution。
定义从概率论和统计学角度看,Weibull Distribution是连续性的概率分布,其概率密度为:其中,x是随机变量,λ>0是比例参数(scale parameter),k>0是形状参数(shape parameter)。
显然,它的累积分布函数是扩展的指数分布函数,而且,Weibull distribution与很多分布都有关系。
如,当k=1,它是指数分布;k=2且时,是Rayleigh distribution(瑞利分布)。
性质(Properties)均值(mean),其中,Г是伽马(gamma)函数。
方差(variance)偏度(skewness)峰度(kurtosis)应用工业制造研究生产过程和运输时间关系。
极值理论预测天气可靠性和失效分析雷达系统对接受到的杂波信号的依分布建模。
Weibull分布(韦伯分布、威布尔分布)
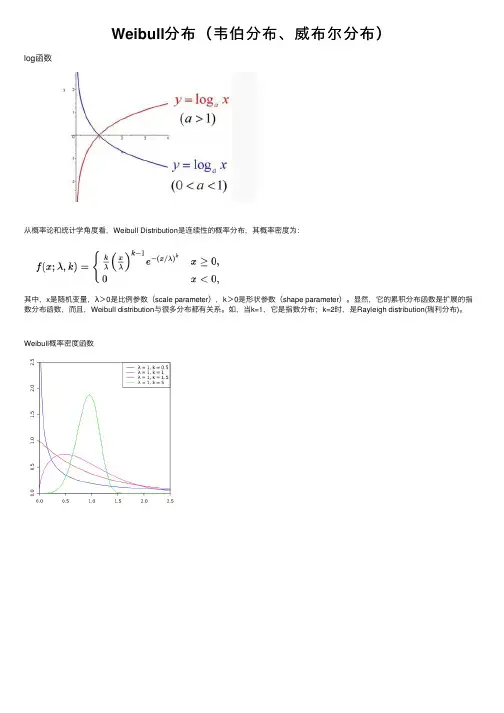
log函数
从概率论和统计学⾓度看,Weibull Distribution是连续性的概率分布,其概率密度为:
其中,x是随机变量,λ>0是⽐例参数(scale parameter),k>0是形状参数(shape parameter)。
显然,它的累积分布函数是扩展的指数分布函数,⽽且,Weibull distribution与很多分布都有关系。
如,当k=1,它是指数分布;k=2时,是Rayleigh distribution(瑞利分布)。
Weibull概率密度函数
k <1的值表⽰故障率随时间减⼩。
如果存在显着的“婴⼉死亡率”或有缺陷的物品早期失效,并且随着缺陷物品被除去群体,故障率随时间降低,则发⽣这种情况。
在创新扩散的背景下,这意味着负⾯的⼝碑:危险功能是采⽤者⽐例的单调递减函数;
k = 1的值表⽰故障率随时间是恒定的。
这可能表明随机外部事件正在导致死亡或失败。
威布尔分布减⼩到指数分布;
k> 1的值表⽰故障率随时间增加。
如果存在“⽼化”过程,或者随着时间的推移更可能失败的部分,就会发⽣这种情况。
在创新扩散的背景
下,这意味着积极的⼝碑:危险功能是采⽤者⽐例的单调递增函数。
该函数⾸先是凹的,然后是凸的,拐点为
Weibull累计分布函数。

威布尔分布参数估计的计算程序威布尔分布是一种常见的概率分布,常用于描述可靠性和寿命数据。
在实际应用中,我们经常需要根据一组观测数据来估计威布尔分布的参数,从而对未来的事件进行预测和分析。
本文将介绍一种基于最大似然估计方法的威布尔分布参数的计算程序。
我们需要明确威布尔分布的定义和参数。
威布尔分布是一个连续概率分布,其概率密度函数为:f(x;λ,k) = (k/λ) * (x/λ)^(k-1) * exp(-(x/λ)^k)其中,λ为尺度参数,k为形状参数。
λ控制了威布尔分布的位置,k则决定了分布的形状。
通过估计这两个参数,我们可以得到对未来事件的预测。
接下来,我们将介绍一种基于最大似然估计方法的参数估计程序。
最大似然估计是一种常用的统计方法,用于根据观测数据来估计分布的参数。
在威布尔分布的参数估计中,最大似然估计方法可以通过最大化似然函数来得到参数的估计值。
似然函数是指在给定观测数据的情况下,参数取值的可能性。
对于威布尔分布,我们可以将似然函数定义为观测数据的概率密度函数的乘积。
然后,我们需要通过最大化似然函数来找到使观测数据最有可能发生的参数取值。
具体来说,我们可以通过以下步骤来计算威布尔分布的参数估计值:1. 收集观测数据:首先,我们需要收集一组与威布尔分布相关的观测数据。
这些观测数据可以是产品的寿命数据、设备的故障时间等。
2. 构建似然函数:根据收集到的观测数据,我们可以构建似然函数。
对于威布尔分布,似然函数可以表示为观测数据的概率密度函数的乘积。
3. 最大化似然函数:接下来,我们需要通过最大化似然函数来找到使观测数据最有可能发生的参数取值。
这可以通过数值优化算法来实现,例如梯度下降算法或牛顿法。
4. 参数估计结果:最后,通过最大化似然函数得到的参数取值就是威布尔分布的参数估计结果。
这些参数可以用来对未来事件进行预测和分析。
需要注意的是,对于威布尔分布的参数估计,我们需要确保观测数据满足威布尔分布的假设。

威布尔分布的概率密度函数
威布尔分布是概率统计学中一种重要的概率分布,它常用于描述可靠性分析、生存分析等领域。
威布尔分布的概率密度函数为:
f(x) = (a/λ) * (x/λ)^(a-1) * e^(-(x/λ)^a) 其中,a和λ是分布的参数,a称为形状参数,λ称为尺度参数。
威布尔分布的累积分布函数为:
F(x) = 1 - e^(-(x/λ)^a)
威布尔分布的特点是随着x的增大,概率密度逐渐减小,但是减小的速率逐渐变缓。
因此,威布尔分布常用于描述在使用寿命较长的物品中,设备失效的概率随时间增加的规律。
在可靠性分析中,威布尔分布常用于估计设备的失效概率曲线和寿命分布。
- 1 -。

威布尔分布的形状参数威布尔分布是一种常用的概率分布,它是统计学中的重要工具之一。
该分布的形状参数决定了其概率密度函数的形状,因此对于理解威布尔分布的性质和应用具有重要的指导意义。
首先,让我们来了解一下威布尔分布的形状参数的定义。
形状参数是威布尔分布的一个重要特征,用β表示。
β大于1时,概率密度函数的形状呈现出右偏斜;β小于1时,概率密度函数的形状呈现出左偏斜;β等于1时,概率密度函数的形状为指数分布。
威布尔分布的形状参数不仅影响了概率密度函数的形状,还直接影响了其均值和方差。
具体来说,威布尔分布的均值μ和方差σ²可以通过以下公式计算:μ = γ(1 + 1/β)σ² = γ²(1 + 2/β) - μ²其中,γ为尺度参数,表示概率密度函数的放缩程度。
可以看出,当β大于1时,威布尔分布的均值和方差均增加;当β小于1时,威布尔分布的均值和方差均减小;当β等于1时,威布尔分布的均值和方差保持不变。
威布尔分布的形状参数还与分布的峰度和偏度有密切关系。
峰度描述了概率密度函数的峰值陡峭程度,而偏度则描述了概率密度函数的对称性。
威布尔分布的峰度和偏度分别为:峰度= 3(1 + 1/β)³ / (1 + 2/β)² - 3偏度= 4(β - 1)² / (1 + 2/β)³从以上公式可以看出,当β大于1时,威布尔分布的峰度增加,整体呈现出尾部较重的形态;当β小于1时,威布尔分布的峰度减小,呈现出尾部较轻的形态;当β等于1时,威布尔分布的峰度保持不变。
在实际应用中,威布尔分布经常用于描述随机事件的持续时间、存活时间等。
例如,对于产品的寿命分析,可以使用威布尔分布来估计产品的失效时间。
此外,威布尔分布还常用于可靠性和风险分析领域。
总结来说,威布尔分布的形状参数决定了其概率密度函数的形状,直接影响了分布的均值、方差、峰度和偏度。
了解和理解威布尔分布的形状参数对于正确应用该分布进行数据分析和预测具有重要的指导意义。


风能资源统计与计算——威布尔(Weibull)分布
来源:作者:佚名发布时间: 2008-8-27 13:29:15
关于风速的分布,国外有过不少的研究,近年来国内也有探讨。
风速分布一般均为正偏态分布,一般说,风力愈大的地区,分布曲线愈平缓,峰值降低右移。
这说明风力大的地区,一般大风速所占比例也多。
如前所述,由于地理、气候特点的不同,各种风速所占的比例有所不同。
通常用于拟合风速分布的线型很多,有瑞利分布、对数正态分布、 分布、双参数威布尔分布、三参数威布尔分布等,也可用皮尔逊曲线进行拟合。
但威布尔分布双参数曲线,普遍认为适用于风速统计描述的概率密度函数。
图13:威布尔分布双参数曲线。

三参数威布尔分布函数威布尔分布是一种常见的概率分布,常用于描述可靠性分析和寿命预测。
它是一种连续概率分布,通常用于模拟和分析具有正向倾斜和递增失败率的数据。
威布尔分布的概率密度函数(PDF)可以用以下公式表示:f(x; λ, k) = (k/λ) * (x/λ)^(k-1) * exp(-(x/λ)^k)其中,x是随机变量的值,λ是尺度参数(scale parameter),k是形状参数(shape parameter)。
尺度参数决定了随机变量的尺度和单位,形状参数决定了随机变量分布的形状。
威布尔分布的累积分布函数(CDF)可以用以下公式表示:F(x; λ, k) = 1 - exp(-(x/λ)^k)威布尔分布的可靠性函数(Reliability Function)可以用以下公式表示:R(x; λ, k) = 1 - F(x; λ, k) = exp(-(x/λ)^k)可靠性函数描述了在给定时间内系统/产品不会发生故障或失效的概率。
威布尔分布的均值(Mean)和方差(Variance)可以用以下公式计算:Mean = λ * Γ(1 + 1/k)Variance = λ^2 *Γ(1 + 2/k) - (λ * Γ(1 + 1/k))^2其中,Γ()是伽玛函数,它可以通过数值方法或查找表来计算。
威布尔分布的特点是,随着时间的推移,失效率(即故障发生的概率密度函数)会逐渐增加,因此可以用于描述由老化过程引起的系统故障。
形状参数k越小,分布越接近指数分布(Exponential Distribution),形状参数k越大,分布越接近于正态分布(Normal Distribution)。
威布尔分布在实际应用中具有广泛的应用,例如在工程、医学、金融等领域。
在工程中,威布尔分布常用于可靠性分析、系统寿命预测和故障诊断。
在医学中,威布尔分布常用于描述疾病的生存时间和患者的生存率。
在金融中,威布尔分布常用于分析金融产品的寿命和市场风险。
威布尔分布是一种常见的概率分布,在许多领域都有着重要的应用。
在统计学中,我们经常需要对数据进行概率分布的估计,以便做出进一步的推断和分析。
而其中一种常见的估计方法就是极大似然估计。
本文将就威布尔分布的极大似然估计过程进行详细的介绍和分析。
一、威布尔分布的概述威布尔分布是描述事件发生时间的概率分布,常用于可靠性分析中。
它的概率密度函数可以写为:f(x|λ, k) = (k/λ) * (x/λ)^(k-1) * exp(-(x/λ)^k)其中,λ和k是分布的参数,λ>0,k>0。
威布尔分布具有灵活的形状,可以适应各种类型的数据分布。
二、极大似然估计的原理极大似然估计是一种常用的参数估计方法,通过最大化样本的似然函数(概率密度函数的乘积)来确定参数的值。
具体来说,对于给定的样本,我们希望找到一组参数,使得观测到这组样本的概率最大。
我们要找到能最好地“解释”已有数据的参数值,这就是极大似然估计的基本原理。
三、威布尔分布的极大似然估计过程对于威布尔分布的参数λ和k的极大似然估计过程,我们可以按照以下步骤来进行:1. 构造似然函数我们需要构造威布尔分布的似然函数。
对于给定的样本x1, x2, ..., xn,其似然函数可以写为:L(λ, k|x1, x2, ..., xn) = ∏[i=1->n] (k/λ) * (xi/λ)^(k-1) * exp(-(xi/λ)^k)2. 求对数似然函数由于对数函数是单调递增的,对数似然函数和似然函数在参数估计中具有相同的极值点。
我们可以对似然函数取对数,得到对数似然函数:l(λ, k|x1, x2, ..., xn) = ∑[i=1->n] (log(k) - log(λ) + (k-1)*log(xi/λ) - (xi/λ)^k)3. 求偏导数接下来,我们需要对对数似然函数分别对λ和k求偏导数,并令偏导数为0,得到参数λ和k的估计值。
4. 求解参数通过求解偏导数为0的方程组,我们可以得到参数λ和k的极大似然估计值。
指数威布尔分布指数威布尔分布是一种常见的概率分布,它在可靠性工程、生物学、医学、金融等领域中得到广泛应用。
本文将介绍指数威布尔分布的定义、特点、应用以及如何进行参数估计。
指数威布尔分布是由指数分布和威布尔分布组合而成的一种概率分布。
它的概率密度函数为:$$f(x)=\frac{\beta}{\alpha}(\frac{x}{\alpha})^{\beta-1}e^{-(\frac{x}{\alpha})^{\beta}}$$其中,$\alpha$和$\beta$是分布的参数,$\alpha>0$,$\beta>0$。
指数威布尔分布的累积分布函数为:$$F(x)=1-e^{-(\frac{x}{\alpha})^{\beta}}$$指数威布尔分布具有以下特点:1. 分布形状:指数威布尔分布的形状由参数$\beta$决定,当$\beta=1$时,分布退化为指数分布;当$\beta>1$时,分布呈现出右偏的形态;当$\beta<1$时,分布呈现出左偏的形态。
2. 可靠性:指数威布尔分布在可靠性工程中得到广泛应用,它可以用来描述产品的寿命分布。
当$\beta=1$时,分布具有无记忆性,即寿命的分布不受之前的使用情况影响;当$\beta>1$时,分布具有加速寿命特性,即寿命随时间的增加而逐渐减少;当$\beta<1$时,分布具有减速寿命特性,即寿命随时间的增加而逐渐增加。
3. 参数估计:指数威布尔分布的参数估计可以使用最大似然估计法或贝叶斯估计法。
最大似然估计法是一种常用的参数估计方法,它通过最大化样本的似然函数来估计参数值。
贝叶斯估计法则是一种基于贝叶斯定理的参数估计方法,它将参数看作是随机变量,通过先验分布和样本数据来计算后验分布,从而得到参数的估计值。
4. 应用:指数威布尔分布在生物学、医学、金融等领域中也有广泛应用。
例如,在医学领域中,可以使用指数威布尔分布来描述疾病的潜伏期分布;在金融领域中,可以使用指数威布尔分布来描述股票价格的波动分布。
威布尔分布和s-n曲线的关系
威布尔分布和S-N曲线之间存在一定的关系。
威布尔分布是一种概率分布,描述的是物体在应力作用下的疲劳寿命。
它的概率密度函数可以表示为:
f(t) = (β/θ) * (t/θ)^(β-1) * exp(-(t/θ)^β)
其中,t表示寿命,θ表示形状参数,β表示尺度参数。
S-N曲线(应力-寿命曲线)则是一种描述材料疲劳寿命与应力之间关系的经验曲线。
它表明当应力作用于材料时,材料的疲劳寿命会随着应力的增加而减少。
威布尔分布和S-N曲线的关系在于,不同形状参数和尺度参数的威布尔分布可以对应不同的S-N曲线形状。
通过选择不同的参数值,可以得到适应不同材料的S-N曲线。
例如,较小的形状参数和尺度参数可以得到S-N曲线的陡峭段,表示材料的疲劳寿命随应力的增加而急剧减少;较大的参数值则表示疲劳寿命与应力呈现更平缓的关系。
因此,威布尔分布可以用来描述材料的疲劳寿命分布情况,而S-N曲线则是一种直观的图像化表示方式,可以用于评估材料的疲劳寿命特性。
三参数威布尔分布威布尔分布是一种常用的概率分布函数,它常常用于描述寿命数据和可靠性分析中的失效率。
三参数威布尔分布是威布尔分布的一种常见形式,它具有更灵活的参数化形式,可以更好地拟合实际数据。
f(x; γ, β, η) = γ/β * [(x - η)/β]^(γ-1) * exp[-((x - η)/β)^γ]其中,x是随机变量,γ、β和η是分布的参数,γ>0,β>0,η为实数。
参数γ被称为形状参数,控制分布的形状。
当γ=1时,威布尔分布变为指数分布。
当γ>1时,分布呈现右偏形态,当γ<1时,分布呈现左偏形态。
参数β被称为尺度参数,控制威布尔分布的变异程度和概率密度函数变化的速率。
当β越大时,分布越陡峭;当β越小时,分布越平缓。
参数η被称为位置参数,控制分布在横轴的位置。
当η=0时,分布在原点处。
F(x; γ, β, η) = 1 - exp[-((x - η)/β)^γ]威布尔分布具有重要的可靠性分析应用。
利用该分布,可以计算系统在不同寿命下的失效概率。
由于三参数威布尔分布更灵活,因此在实际应用中更为常见。
在可靠性工程中,三参数威布尔分布通常用于描述已经运行一段时间的系统的可靠性分析。
通过对系统失效数据进行统计,可以得到最适合的参数估计,从而预测系统在不同寿命下的失效概率。
为了估计三参数威布尔分布的参数,可以使用最大似然估计法。
该方法通过最大化似然函数,找到最适合的参数估计值。
同时,也可以使用图形法和统计软件进行参数估计。
对于随机变量X满足三参数威布尔分布,其期望和方差分别为:E(X)=η+β*Γ(1+1/γ)Var(X) = β^2 * [ Γ(1+2/γ) - Γ^2(1+1/γ) ]其中,Γ(·)表示伽玛函数。
总之,三参数威布尔分布是一种常用的概率分布函数,适用于可靠性分析和寿命数据分析。
通过研究该分布的特性和参数估计方法,可以更好地理解和应用该分布,为工程师提供决策支持和改进策略。