简单介绍流体的连续性方程

vof 连续方程
VOF（Volume of Fluid）方法是一种常用的流体模拟方法，用于模拟多相流体的运动和相界面的变化。

在VOF方法中，连续方程是其中一个关键的方程，用于描述流体的质量守恒。

连续方程是基于质量守恒原理，描述了流体在空间和时间上的连续性，即质量在流体中的守恒。

对于单相流体，连续方程可以表示为：
∂ρ/∂t + ∇·(ρu) = 0
其中，∂ρ/∂t 是流体密度ρ对时间的变化率，∇·表示散度算子，用于求取速度矢量u的散度，ρu 是流体密度ρ和速度矢量u的乘积。

对于多相流体中的VOF方法，连续方程的形式有所变化，用于描述流体的分区和界面的变化。

连续方程可以表示为：∂(φρ)/∂t + ∇·(φρu) = 0
其中，φ 是用于表示单元格中的流体体积分数的变量，用于区别不同的相（如空气和水），(φρ) 是流体体积分数φ和密度ρ的乘积。

连续方程的求解可以采用数值方法，如有限差分、有限元、体积法等。

在VOF方法中，连续方程通常与其他方程（如动量方程、相间力平衡方程等）一起求解，以模拟多相流体的运动和相界面的变化。

连续方程的求解将提供流体体积分数φ的分布，从而确定不同相的位置和界面的移动。

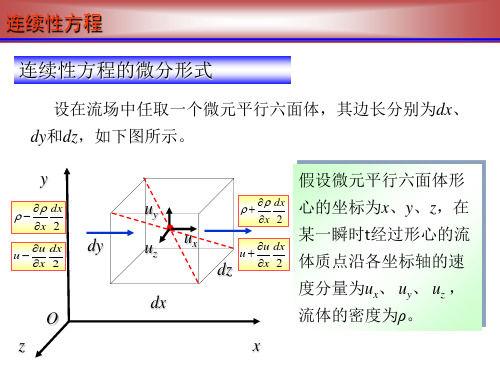
流体力学是研究流体运动和力学的学科，涉及流体的运动规律、压力、密度等物理性质。

在流体力学的研究中，三大方程公式是非常重要的理论基础，它们分别是连续方程、动量方程和能量方程。

本文将对这三大方程公式及其符号含义进行详细介绍。

一、连续方程连续方程是描述流体连续性的重要方程，它表达了流体在运动过程中质点的连续性。

连续方程的数学表达式为：\[ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0 \]其中，符号和含义说明如下：1.1 ∂ρ/∂t：表示密度随时间的变化率，ρ为流体密度。

1.2 ∇·(ρv)：表示流体质量流动率的散度，∇为Nabla算子，ρv为流体的质量流速矢量。

这一方程表明了在运动的流体中，质量是守恒的，即单位体积内的质量永远不会减少，这也是连续方程的基本原理。

二、动量方程动量方程描述了流体运动过程中动量的变化和传递，是流体力学中的核心方程之一。

其数学表达式为：\[ \frac{\partial (\rho \mathbf{v})}{\partial t} + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = -\nabla p + \nabla \cdot \mathbf{\tau} + \mathbf{f} \]其中，符号和含义说明如下：2.1 ∂(ρv)/∂t：表示动量随时间的变化率。

2.2 ∇·(ρv⃗v)：表示动量流动率的散度。

2.3 -∇p⃗：表示流体受到的压力梯度力。

2.4 ∇·τ⃗：表示应力张量的散度，τ为流体的粘性应力张量。

2.5 f⃗：表示单位体积内流体受到的外力。

动量方程描述了流体内部和外部力之间的平衡关系，它是研究流体运动规律和动力学行为的重要方程。

三、能量方程能量方程描述了流体在运动过程中的能量变化规律，包括内能、压力能和动能等能量形式。