2017-2018学年陕西省咸阳市三原县北城中学高二(下)第一次月考数学试卷(文科) Word版含解析
- 格式:doc
- 大小:200.03 KB
- 文档页数:8

1第I 卷(选择题,共75分)一、选择题(本大题共15个小题,每小题5分,共75分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.数列1,3,6,10,15,…的递推公式可能是A. ⎩⎪⎨⎪⎧ a1=1,an +1=an +n(n ∈N*)B. ⎩⎪⎨⎪⎧a1=1,an =an -1+n(n ∈N*,n≥2) C. ⎩⎪⎨⎪⎧ a1=1,an +1=an +(n -1)(n ∈N*) D. ⎩⎪⎨⎪⎧a1=1,an =an -1+(n -1)(n ∈N*,n≥2)2.下列求导数运算正确的是A .211)1(x x x +='+ B .2ln 1)(log 2x x =' C .ex x 3log 3)3(=' D .x x x x sin 2)cos (2-=' 3.观察710>58,911>810,1325>921,…若a>b>0且m>0,则b +m a +m与a b之间大小关系为A .相等B .前者大C .后者大D .不确定4.曲线x x y 43-=在点(1,3)-处的切线倾斜角为 A. 34πB. 2πC. 4πD. 6π5.用数学归纳法证明等式2)4)(3()3(321++=+++++n n n (n ∈N*)时,验证1=n ,左边应取的项是A .1B .1+2C .1+2+3D .1+2+3+4 6.已知a +b +c =0,则ab +bc +ca 的值A .大于0B .小于0C .不小于0D .不大于07.若凸k 边形的内角和为)(k f ,则凸1+k 边形的内角和)1(+k f (3≥k 且k ∈N*)等于 A .f(k)+π2 B .f(k)+π C .f(k)+32π D .f(k)+2π8.设y yx x B y x y x A y x +++=+++=>>11,1,0,0,则A 与B 的大小关系为A .B A > B .B A ≥C .B A <D .B A ≤9.32()32f x ax x =++,若(1)4f '-=, 则a 的值等于2A .310B. 313C. 316D.31915.若曲线4x y =的一条切线与直线084=-+y x 垂直,则l 的方程为A .034=--y xB .054=-+y xC .034=+-y xD . 034=++y x 第II 卷(非选择题,共75分)二、填空题(本大题共5个小题,每小题5分,共25分.将正确答案填在题中横线上) 16.观察①sin210°+cos240°+sin10°cos40°=34; ②sin26°+cos236°+sin6°cos36°=34.两式的结构特点可提出一个猜想的等式为________________.17. 某物体做直线运动,其运动规律是t t s 32+= ( t 的单位是秒,s 的单位是米),则它在4秒末的瞬时速度为 .18.已知)2(3)(2f x x x f '+=,则)2(f '=________. 19.设函数)(x f 定义如下表,数列{}n x 满足50=x ,且对任意的自然数均有)(1n n x f x =+,则2013x =________________.x 1 2 3 4 5 f(x)41352320. 设等差数列{an}的前n 项和为Sn , 则S4,S8-S4,S12-S8,S16-S12成等差数列.类比以上结论有:设等比数列{bn}的前n 项积为Tn ,则T4,_______,______,T16T12 成等比数列.三、解答题(本大题共4个小题,共50分.解答应写出文字说明、证明过程或演算步骤) 21. (本题12分)求下列函数的导数.(1) 453223-+-=x x x y (2)82)21(x y += 22.(本题12分)已知:1,0,0=+>>y x y x ,求证: 9)11)(11(≥++y x23.(本小题满分12分)已知抛物线c bx ax y ++=2通过点()1,1P ,且在点)1,2(-Q 处与直线3-=x y 相切,求实数c b a ,,的值。
陕西省三原县北城中学 高二下学期第一次月考数学(文)试题第I 卷(选择题)s一、选择题:(每题5分 共60分)一、对变量x 、y 有观测数据(xi ,yi )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(ui ,vi )(i=1,2,…,10),得散点图2.由这两个散点图能够判定( )A 、变量x 与y 正相关,u 与v 正相关B 、变量x 与y 正相关,u 与v 负相关C 、变量x 与y 负相关,u 与v 正相关D 、变量x 与y 负相关,u 与v 负相关二、已知1a =3,1+n a =33+nna a ,试通过计算2a ,3a ,4a ,5a 的值推测出n a =A 、n 23B 、n 3C 、n 4D 、n 23、以下有关三段论推理“自然数都是整数,4是自然数,因此4是整数”的说法正确的选项是A 、推理正确B 、推理形式不正确C 、大前提错误D 、小前提错误 4、将x=2输入以下程序框图(右图),得结果为 A 、3 B 、5 C 、8 D 、12五、如以下图所示的是“概率”知识的 A 、流程图 B 、结构图 C 、程序框图 D 、直方图六、已知x 与y 之间的一组数据:x 0 1 2 3 y1357那么y 与x 的线性回归方程为y =a +bx 必过A 、点(2,2)B 、点(,0)C 、点(1,2)D 、点(,4)7、给出以下五个命题:①将A 、B 、C 三种个体按312的比例分层抽样调查,若是抽取的A 个体为9个,那么样本容量为30; ②一组数据1,2,3,3,4,5的平均数、众数、中位数都相同;③甲组数据的方差为5,乙组数据为5,6,9,10,5,那么这两组数据中比较稳固的是甲;④已知具有相关关系的两个变量知足的回归直线方程为y =1-2x ,那么x 每增加1个单位,y 平均减少2个单位;⑤统计的10个样本数据为125,120,122,105,130,114,116,95,120,134,那么样本数据落在[,内的频率为. 其中真命题为A .①②④B .②④⑤C .②③④D .③④⑤八、用反证法证明命题“若是a >b ,那么33b a >”时,假设的内容应是 A 、33b a = B 、33b a <C 、33b a =且33b a <D 、33b a =或33b a <九、设一个线性回归方程y=3-2x ,变量x 增加一个单位时A 、y 平均增加2个单位B 、y 平均减少3个单位C 、y 平均减少2个单位D 、y 平均增加3个单位10、假设事件E 和事件F 彼此独立,且P(E)=P(F)=41,那么P(EF)的值等于 A 、0 B 、161 C 、41 D 、211一、甲、乙两任抢答竞赛题,甲答对的概率为51,乙答对的概率为41,那么两人恰有一人答对的概率为 A 、207 B 、2012 C 、201 D 、202认为作业多 认为作业不多 合计 喜欢玩电脑游戏 18 9 27 不喜欢玩电脑游戏 8 15 23 合计262450那么以为喜爱玩电脑游戏与以为作业量的多少有关系的把握大约为 A 、99% B 、95% C 、90% D 、无充分依据 二、填空题(每题5分共35分)13、观看右边算式,依照上述规律,那么第五个式 子应为____________1=1 3+5=8 7+9+11=27 13+15+17+19=64…………14、假设执行如下图的框图,输入x1=1,x2=2,x3=4,x4=8,那么输出的数等于___________1五、设ΔABC 的三边长别离为a 、b 、c ,ΔABC 的面积为S ,那么ΔABC 的内切圆半径为2Sr a b c =++,将此结论类比到空间四面体:设四面体S —ABCD 的四个面的面积别离为1S ,2S ,3S ,4S ,体积为V ,那么四面体的内切球半径r = .1六、将下面用分析法证明ab b a ≥+222的步骤补充完整:要证ab b a ≥+222,只需证ab b a 222≥+,也确实是证_______________,即证___________,由于__________显然成立,因此原不等式成立。

陕西省咸阳市三原县北城中学2013-2014学年高二数学上学期第一次月考试题(无答案)北师大版一、选择题:(本大题共13小题,每小题5分,共65分)1、数列 21,61,51,41,31+n 中第6项是( ) A 121 B 81 C 111 D 101 2. 已知数列{}n a ,1n 2+=n a ,那么此数列是( )A .递增数列B .递减数列C .常数列D .摆动数列 3. 12+与12-,两数的等比中项是( )A .1B .1-C .1±D .21 4. 在ABC ∆中,1660=︒=b A ,,面积3220=S ,则a 等于( ) A. 610. B. 75 C. 49 D. 515. 等差数列9}{,7,3,}{51第则数列中n n a a a a ==项等于( )A .9B .10C .11D .126. 已知{}n a 是等比数列,41252==a a ,,则公比q =( ) A .21- B .2- C .2 D .21 7、等差数列{}n a 中11=a ,0≠d ,如果521a a a 、、成等比数列,那么d 等于( )A .3B .2C .-2D .2±8.一个三角形的三个内角A 、B 、C 成等差数列,那么()tan A C +的值是 ( )A ...不确定 9. 在ABC ∆中,︒===452232B b a ,,,则A 为( )A B C D ....60120603015030︒︒︒︒︒︒或或10.三角形的两边分别为5和3,其夹角余弦是06752=--x x 的根,则另一边长为( )A. 52B. 213C. 16D. 411.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为 ( )A 、锐角三角形B 、直角三角形C 、钝角三角形D 、由增加的长度决定12、 数列{a n }的通项公式是a n =1(1)n n +(n ∈N*),若前n 项的和为1011,则项数n 为( ) A .12 B .11C .10D .9 13、已知△ABC 中三个内角为A 、B 、C 所对的三边分别为a 、b 、c ,设向量 (,)p a c b =+,(,)q b a c a =--.若//p q ,则角C 的大小为 ( )A . 6πB .3πC .2πD . 23π二、填空题:(本大题共7小题,每小题5分,共35分.把答案填在答题卷的相应位置上.14、等差数列2,5,8,…的第20项是15.在等比数列{}n a 中, 若101,a a 是方程06232=--x x 的两根,则47a a ⋅=___________. 16.等差数列{}n a 的前m 项的和是30,前2m 项的和是100,则它的前3m 项的和是17、在△ABC 中,角B=60且边b=2,则△ABC 外接圆的半径R=18.在△ABC 中,3,4AB BCAC ===,则AC 上的高为 19. ∆ABC 中,a=2,A= 30,C= 45,则∆ABC 的面积为20.数列{}n a 中,112a =,111(1)n na n a +=-≥,则2006a = 。

北城中学2017-2018学年度第一学期第一次月考试题高二数学试题一、选择题(每小题5分共计60分)1、数列1,-3,5,-7,9,…的一个通项公式为( )A .12-=n a nB .)12()1(--=n a n nC .)21()1(n a n n --=D .)12()1(+-=n a n n 2、等比数列2,4,8,16,…的前n 项和为( ) A .121-+n B .22-n C .n 2 D .221-+n3、等比数列{}n a 中,已知112733n a a q ===,,,则n 为( ) A .3 B .4 C .5 D .6 4、等比数列{}n a 中,9696==a a ,,则3a 等于( ) A .3 B .23C .916 D .4 5、若数列{}n a 中,n a =43-3n ,则n S 最大值n= ( )A .13B .14C .15D .14或156、等差数列{}n a 的首项11=a ,公差0≠d ,如果521a a a 、、成等比数列,那么d 等于( )A .3B .2C .-2D .2±7、等差数列{}n a 的前m 项的和是30,前2m 项的和是100,则它的前3m 项的和是( )A .130B .170C .210D .260 8、 数列{a n }的通项公式是a n =1(1)n n +(n ∈N*),若前n 项的和为1011,则项数n 为( )A .12B .11C .10D .99.若c b a ,,成等比数列,则函数c bx ax y ++=2的图像与x 轴交点个数是( )A.0B.1C.2D. 20或 10.已知{}n a ,{}n b 都是等比数列,那么( ) A.{}n n b a +,{}n n b a ⋅都一定是等比数列B. {}n n b a +一定是等比数列,但{}n n b a ⋅不一定是等比数列C. {}n n b a +不一定是等比数列,但{}n n b a ⋅一定是等比数列D. {}n n b a +,{}n n b a ⋅都不一定是等比数列 11.已知1是a 2与b 2的等比中项,又是a1与b 1的等差中项,则22b a b a ++的值是( )A .1或21B .1或-21C .1或31D .1或-3112.已知数列{a n }满足1+n a =1-na 1(n ∈N *),且1a =2,则2017a =()A .-1B .21C .23D .2二、填空题(每小题5分共计20分)13、等差数列{}n a 中,n S =40,1a =13,d =-2 时,n =______________ 14、数列{}a n 为等差数列,且14739a a a++=,25833a a a++=,则=++a a a 963_______15、在等差数列{}n a 中,35791120a a a a a ++++=,则113a a += __________16、.三个数成等比数列,它们的和为14,它们的积为64,则这三个数为 三、解答题(写出简要的解体过程)17、(本题10分)求数列11111,2,3,424816…的前n 项和。

一、选择题(每小题5分,共计65分)1、数列1,-3,5,-7,9,的一个通项公式为( )A .12-=n a nB .)12()1(--=n a nn C .)21()1(n a n n --= D .)12()1(+-=n a nn2.在等比数列}{n a 中,,8,1641=-=a a 则=7a ( )A 4-B 4±C 2-D 2± 3.如图,这是一个正六边形的序列,则第(n )个图形的边数为( ).A. 5 n -1B. 6 nC. 5 n +1D.4 n +2 4、等差数列{}n a 中,已知a 1 + a 15=4,则a 8等于( )A .-2或2B .2C .1D .2或-15.等比数列{a n }的前3项的和等于首项的3倍,则数列的公比为( )A .245 B .12 C .445D .6 6、等差数列{}n a 的首项11=a ,公差0≠d ,若521a a a 、、成等比数列,则 d 为( ) A .3 B .2 C .-2 D .2±7.在数列1,1,2,3,5,8,x,21,34,55中,x 等于( )A.11B.12C.13D.14 8、一个三角形的三个内角A 、B 、C 成等差数列,那么()tan A C +的值是A B .C . D .不确定 9. 在正项的等比数列{}n a ,若a 5 a 6=9,则log 3 a 1+log 3a 2+log 3 a 3+…+ log 3 a 10等于( ) A.8 B.10 C.12 D.2+ log 3510、、等比数列{}n a 的前m 项的和是30,前2m 项的和是90,则它的前3m 项的和是( ) A .130 B .170 C .210 D .26011、一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是( )A.-2B.-3C.-4D.-512.已知数列10,…10…,使数列前n 项的乘积不超过10最小正整数n 是(A)9 (B)10 (C)11 (D)1213、如图所示的5×5正方形表格中尚有20个空格,若在每一个空格中填入一个正整数,使得每一行和每一列都成等差数列,则字母a 所代表的正整数是(A )16 (B )17 (C )18 (D )19二、填空题(每小题5分,共计35分)14、在等差数列{ a n }中, a 2 =-5,a 6= a 4 +6,则a 1等于______________ 15. 等比数列的公比为2, 且前4项之和等于30, 那么前8项之和等于16、若数列{}n a 的前n 项和n S =22n n -,则其通项公式=n a ____ .17、成等差数列的三个数的和为12,第二数与第三数之积为24,则这三个数是___ 。

2014-2015学年陕西省咸阳市三原县北城中学高二(下)第一次月考数学试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共12小题,共60.0分)1.归纳推理是()A.特殊到一般的推理B.特殊到特殊的推理C.一般到特殊的推理D.一般到一般的推理【答案】A【解析】解:归纳推理是由部分到整体的推理,演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理.故A中结论正确,故选:A本题考查的知识点是归纳推理、类比推理和演绎推理的定义,根据定义对4个命题逐一判断即可得到答案.判断一个推理过程是否是归纳推理关键是看他是否符合归纳推理的定义,即是否是由特殊到一般的推理过程.判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义,即是否是由特殊到与它类似的另一个特殊的推理过程.判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义,即是否是由一般到特殊的推理过程.2.若f(x)=cosx,则f′()=()A.-1B.C.0D.1【答案】A【解析】解:∵f′(x)=-sinx,∴f′()=-sin=-1,故选:A根据基本函数的导数公式求导,然后代入求值即可本题考查了导数的运算,属于基础题3.已知f(x)=,则的值是()A. B.2 C.- D.-2【答案】A解:因为f(x)=,所以===,故选:A.利用导数的定义,代入计算即可,本题主要考查了导数的定义,属于基础题.4.物体作直线运动的方程为s=s(t),则s′(4)=10表示的意义是()A.经过4s后物体向前走了10mB.物体在前4s内的平均速度为10m/sC.物体在第4s内向前走了10mD.物体在第4s时的瞬时速度为10m/s【答案】D【解析】解:∵物体作直线运动的方程为s=s(t),根据导数的物理意义可知,S(t)函数的导数即是t时刻的瞬时速度.∴s′(4)=10表示的意义是物体在第4s时的瞬时速度为10m/s.故选D.根据导数的物理意义可知,S(t)函数的导数即是t时刻的瞬时速度.本题考察了导数的物理意义,函数的导数与瞬时速度的关系是解决本题的关键.5.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是()A.假设三内角都不大于60度B.假设三内角都大于60度C.假设三内角至多有一个大于60度D.假设三内角至多有两个大于60度【答案】B【解析】解:根据反证法的步骤,假设是对原命题结论的否定,“至少有一个”的否定:“一个也没有”;即“三内角都大于60度”.故选B一些正面词语的否定:“是”的否定:“不是”;“能”的否定:“不能”;“都是”的否定:“不都是”;“至多有一个”的否定:“至少有两个”;“至少有一个”的否定:“一个也没有”;“是至多有n个”的否定:“至少有n+1个”;“任意的”的否定:“某个”;“任意两个”的否定:“某两个”;“所有的”的否定:“某些”.本题考查反证法的概念,逻辑用语,否命题与命题的否定的概念,逻辑词语的否定.6.若f(x)=x3,f′(x0)=3,则x0的值为()A.1B.-1C.1或-1D.或-【答案】C【解析】解:∵f(x)=x3,∴f′(x)=3x2,则f′(x0)=3x02=3,故选:C.先对函数f(x)进行求导,然后将x0代入导函数建立等量关系,求出x0即可本题主要考查了导数的运算,以及导数的几何意义,属于基础题7.如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=()A. B.3 C.4 D.5【答案】A【解析】解:由图可知,f(4)=5,又直线过(0,3),(4,5),∴,即f′(4)=.故选:A.由图得到f(4)=5,进一步得到直线l所经过的两点,由两点求斜率得到l的斜率,即曲线y=f(x)在x=4处的导数值.本题考查利用导数研究曲线上某点处的切线方程,考查了导数的几何意义,是中低档题.8.满足f(x)=f′(x)的函数是()A.f(x)=1-xB.f(x)=xC.f(x)=0D.f(x)=1【答案】C【解析】解:A、由f(x)=1-x,得到f′(x)=-1≠1-x=f(x),本选项错误;B、由f(x)=x,得到f′(x)=1≠x=f(x),本选项错误;C、由f(x)=0,得到f′(x)=0=f(x),本选项正确;D、由f(x)=1,得到f′(x)=0≠1=f(x),本选项错误,故选C分别利用求导法则求出各项的导函数f′(x),即可判断f(x)=f′(x)的函数,得到正确答案.此题考查学生灵活运用求导的法则化简求值,是一道基础题.9.已知质点按规律s=2t2+4t(距离单位:m,时间单位:s)运动,则其在t=3s时的瞬时速度为()(单位:m/s).A.30B.28C.24D.16【答案】D解:∵s=2t2+4t,∴s'=s'(t)=4t+4∴当t=3时,s'(3)=4×3+4=16,故选:D根据导数的物理意义求函数的导数即可.本题主要考查导数的物理意义,要求熟练掌握导数的基本运算,比较基础.10.下列式子不正确的是()A.(3x2+cosx)′=6x-sinxB.(lnx-2x)′=ln2C.(2sin2x)′=2cos2xD.()′=【答案】C【解析】解:由复合函数的求导法则对于选项A,(3x2+cosx)′=6x-sinx成立,故A正确对于选项B,′成立,故B正确对于选项C,(2sin2x)′=4cos2x≠2cos2x,故C不正确对于选项D,′成立,故D正确故选C观察四个选项,是四个复合函数求导的问题,故依据复合函数求导的法则依次对四个选项的正误进行判断即可.本题考查了复合函数的求导法则,求解中要特别注意复合函数的求导法则(2sin2x)′=2cos2x•(2x)'=4cos2x,对函数的求导法则要求熟练记忆,本题属于基础题.11.若a1=12,a2=12+22+12,…,a n=12+22+…+n2+…+22+12,在运用数学归纳法证明a n=n(2n2+1)时,第二步中从k到k+1应添加的项是()A.k2+1B.(k2+1)2C.(k+1)2+k2D.(k+1)2+2k2【答案】C【解析】解:∵a k=12+22+…+k2+…+22+12,a k+1=12+22+…+k2+(k+1)2+k2+…+22+12,∴在运用数学归纳法证明a n=n(2n2+1)时,第二步中从k到k+1应添加的项是(k+1)2+k2,故选:C.a k=12+22+…+k2+…+22+12,a k+1=12+22+…+k2+(k+1)2+k2+…+22+12,即可得出结论.本题考查数学归纳法的运用,考查学生分析解决问题的能力,属于基础题.12.已知函数f(x)=x3-2x2+3x+,则与f(x)图象相切的斜率最小的切线方程为()A.2x-y-3=0B.x+y-3=0C.x-y-3=0D.2x+y-3=0B【解析】解:∵f(x)=x3-2x2+3x+,∴f′(x)=x2-4x+3=(x-2)2-1∵当x=2时,f′(x)取到最小值为-1∴f(x)=x3-2x2+3x+的切线中,斜率最小的切线方程的斜率为-1∵f(2)=1,∴切点坐标为(2,1)∴切线方程为:y-1=-(x-2),即x+y-3=0故选B.先对函数f(x)进行求导,然后求出导函数的最小值,其最小值即为斜率最小的切线方程的斜率,进而可求得切点的坐标,最后根据点斜式可得到切线方程.本题主要考查导数的几何意义和导数的运算.导数的几何意义是函数在某点的导数值等于过该点的切线的斜率的值.二、填空题(本大题共6小题,共30.0分)13.观察下列式子:1+<,1++<,1+++<,…据以上式子可以猜想:1++++…+<______ .【答案】【解析】解:由已知中的不等式:<,<,<…我们可以推断出:右边分式的分母与左右最后一项分母的底数相等,分子是分母的2倍减1,即<,∴<.故答案为:.由已知中的不等式:我们可以推断出:右边分式的分母与左右最后一项分母的底数相等,分子是分母的2倍减1,即<,将n=2015,代入可得答案.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).14.用反证法证明某命题时,对结论“自然数a,b,c中至多有2个偶数”的正确假设为“假设自然数a,b,c中______ ”.【答案】三个数都是偶数【解析】解:用反证法法证明数学命题时,应先假设要证的命题的反面成立,即要证的命题的否定成立,而命题:“自然数a,b,c中至多有2个偶数”的否定为:“三个数都是偶数”,故答案为:三个数都是偶数.用反证法法证明数学命题时,假设命题的反面成立,写出要证的命题的否定形式,即为所求.本题主要考查用反证法法证明数学命题,求一个命题的否定,注意否定词语的应用,属于基础题.15.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:f″(x)是函数y=f(x)的导函数f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))y=f(x)”.有同学发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是“对称中心”.请你将这一发现作为条件,则函数f(x)=x3-3x2+3x的对称中心为______ .【答案】(1,1)【解析】解:∵f'(x)=3x2-6x+3,∴f''(x)=6x-6,令f''(x)=6x-6=0,得x=1.又f(1)=1,所以f(x)的对称中心为(1,1).故答案为:(1,1)根据函数f(x)的解析式求出f′(x)和f″(x),令f″(x)=0,求得x的值本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,函数的对称性的应用,属于基础题.16.已知物体的运动方程为s=t2++lnt-1(t是时间,s是位移),则物体在时刻t=3时的速度为______ .【答案】6【解析】解:物体的运动速度为v(t)=s′=2t-+所以物体在时刻t=3时的速度为v(3)=2×3-+=6,故答案为:6.根据位移的导数是速度,求出s的导函数即速度与时间的函数,将2代入求出物体在时本题考查导数在物理上的应用:对物体位移求导得到物体的瞬时速度.17.已知函数y=f(x)的图象在x=4处的切线方程是y=-2x+9,则f(4)-f′(4)= ______ .【答案】3【解析】解:根据切点在切线上可知当x=4时,y=1∴f(4)=1∵函数y=f(x)的图象在x=4处的切线方程是y=-2x+9,∴f′(4)=-2则f(4)-f′(4)=1-(-2)=3故答案为:3根据切点在切线上可求出f(4)的值,然后根据导数的几何意义求出f′(4)的值,从而可求出所求.本题主要考查了利用导数研究曲线上某点切线方程,以及导数的几何意义,同时考查了运算求解的能力,属于基础题.18.若函数f(x)=x3-f′(-1)•x2+x+5,则f′(-1)= ______ .【答案】-2【解析】解:∵f(x)=x3-f′(-1)•x2+x+5,∴f′(x)=x2-2f′(-1)x+1,取x=-1,得f′(-1)=1+2f′(-1)+1,即f′(-1)=-2.故答案为:-2.求出原函数的导函数,在导函数解析式中取x=-1得答案.本题考查了导数及其运算,解答磁体的关键是明确f′(-1)为常数,是基础题.三、解答题(本大题共5小题,共60.0分)19.求下列函数的导数:(1)f(x)=x3cosx(2)f(x)=(3)f(x)=ln(3x-1)【答案】解:(1)f′(x)=(x3)′cosx+x3(cosx)′=3x2cosx-x3sinx;(2)f′(x)==;(3)f′(x)=(3x-1)′=.【解析】根据导数的公式和导数的运算法则进行求导即可.比较基础.20.已知函数f(x)=e x-x2+a的图象在点x=0处的切线为y=bx(e为自然对数的底数).求函数f(x)的解析式.【答案】解:函数f(x)=e x-x2+a的导数为f′(x)=e x-2x,在点x=0处的切线为y=bx,即有f′(0)=b,即为b=1,即切线为y=x,又切点为(0,1+a),即1+a=0,解得a=-1,即有f(x)=e x-x2-1.【解析】求出f(x)的导数,由切线方程可得切线斜率和切点坐标,可得a=-1,b=1,即可得到f(x)的解析式;本题考查导数的运用:求切线的斜率,主要考查导数的几何意义,直线方程的运用,属于基础题.21.已知函数,其中a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在原点处的切线方程;(Ⅱ)求f(x)的单调区间.【答案】解:(Ⅰ)当a=1时,,′.…(2分)∴f'(0)=2,∵f(0)=0,∴曲线y=f(x)在原点处的切线方程是2x-y=0.…(4分)(Ⅱ)求导函数可得,′.…(6分)当a=0时,′,所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减.…(7分)当a≠0,′.①当a>0时,令f'(x)=0,得x1=-a,,f(x)与f'(x)的情况如下:故f(x)的单调减区间是(-∞,-a),,∞;单调增区间是,.…(10分)②当a<0时,f(x)与f'(x)的情况如下:所以f(x)的单调增区间是∞,,(-a,+∞);单调减区间是,,(-a,+∞).…(13分)综上,a>0时,f(x)在(-∞,-a),,∞单调递减;在,单调递增.a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;a<0时,f(x)在∞,,(-a,+∞)单调递增;在,单调递减.【解析】(Ⅰ)当a=1时,求导函数,确定切点坐标与切线的斜率,即可得到曲线y=f(x)在原点处的切线方程;(Ⅱ)求导函数可得,分类讨论,利用导数的正负,可得函数的单调区间.本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,属于中档题.22.(用分析法或者综合法证明)已知a>6,求证:<.【答案】证明:要证<,只需证明:<,只需证明:<,只需证明:(a-3)(a-6)<(a-4)(a-5),只需证明:a2-9a+18<a2-9a++20,只需证明:18<20,显然成立,所以a>6时,<.【解析】两边平方,化简可得.本题考查用分析法证明不等式,用分析法证明不等式的关键是寻找使不等式成立的充分条件.23.已知数列{a n}的前n项和S n=1-na n(n∈N*)(1)计算a1,a2,a3,a4;(2)猜想a n的表达式,并用数学归纳法证明你的结论.【答案】解:(1)计算得;;;.(2)猜测:.下面用数学归纳法证明①当n=1时,猜想显然成立.②假设n=k(k∈N*)时,猜想成立,即.那么,当n=k+1时,S k+1=1-(k+1)a k+1,即S k+a k+1=1-(k+1)a k+1.又,所以,从而.即n=k+1时,猜想也成立.故由①和②,可知猜想成立.【解析】(1)由S n与a n的关系,我们从n=1依次代入整数值,即可求出a1,a2,a3,a4;(2)由a1,a2,a3,a4的值与n的关系,我们归纳推理出数列的通项公式,观察到它们是与自然数集相关的性质,故可采用数学归纳法来证明.本题(2)中的证明要用到数学归纳法,数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基)P(n)在n=1时成立;2)(归纳)在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.。
2017-2018学年陕西省咸阳市三原县北城中学高二(上)第三次月考数学试卷(文科)一、选择题(本大题共15小题,每小题5分,满分75分)1.命题“若p则q”的逆命题是()A.若q则p B.若¬p则¬q C.若¬q则¬p D.若p则¬q2.在等差数列{a n}中,a1+a9=10,则a5的值为().A.5 B.6 C.8 D.103.命题“对任意x∈R,都有x2≥0”的否定为()A.对任意x∈R,都有x2<0 B.不存在x∈R,都有x2<0C.存在x0∈R,使得x02≥0 D.存在x0∈R,使得x02<04.设抛物线的顶点在原点,准线方程为x=﹣2,则抛物线的方程是()A.y2=﹣8x B.y2=﹣4x C.y2=8x D.y2=4x5.在等比数列{a n}中,a1+a2=2,a3+a4=50,则公比q的值为()A.25 B.5 C.﹣5 D.±56.“1<x<2”是“x<2”成立的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件7.若变量x,y满足约束条件,则z=2x+y的最小值为()A.3 B.2 C.1 D.08.在△ABC中,若∠A=60°,∠B=45°,,则AC=()A. B. C.D.9.已知命题甲:“任意两个数a,b必有唯一的等差中项”,命题乙:“任意两个数a,b必有两个等比中项”.则()A.甲是真命题,乙是真命题B.甲是真命题,乙是假命题C.甲是假命题,乙是真命题D.甲是假命题,乙是假命题10.设a,b,c∈R,且a>b,则()A.ac>bc B.C.a2>b2D.a3>b311.已知双曲线﹣=1的右焦点为(3,0),则该双曲线的离心率等于()A.B.C.D.12.过点(﹣3,2)且与=1有相同焦点的椭圆的方程是()A.=1 B.=1C.=1 D.=113.下列函数中,最小值为4的是()A.y=x+B.y=sinx+(0<x<π)C.y=e x+4e﹣x D.y=+14.若2x+2y=1,则x+y的取值范围是()A.[0,2]B.[﹣2,0] C.[﹣2,+∞)D.(﹣∞,﹣2]15.关于x的不等式x2﹣2ax﹣8a2<0(a>0)的解集为(x1,x2),且:x2﹣x1=15,则a=()A.B.C.D.二、填空题:(本大题共5小题,每小题5分,共25分)16.三角形的一边长为14,这条边所对的角为60°,另两边之比为8:5,则这个三角形的面积为.17.过双曲线左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是.18.对于任意实数x,不等式ax2﹣2x﹣4<0恒成立,则实数a的取值范围是.19.点P是抛物线y2=4x上一动点,则点P到点(0,﹣1)的距离与到抛物线准线的距离之和的最小值是.20.已知命题P:不等式<0的解集为{x|0<x<1};命题q:在△ABC中,“A>B”是“sinA>sinB”成立的必要不充分条件.有下列四个结论:①p真q假;②“p∧q”为真;③“p∨q”为真;④p假q真其中正确结论的序号是.(请把正确结论的序号都填上)三、解答题(本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤)21.已知抛物线的顶点在原点,对称轴为y轴,其上一点A (m,﹣4)到焦点F的距离为6.求抛物线的方程及点A的坐标.22.已知数列{a n}是等差数列,a1=2,a1+a2+a3=12(1)求数列{a n}的通项公式(2)令b n=a n+3n,求{b n}的前n项和.23.已知命题P:(1﹣x)(x+4)≥0,q:x2﹣6x+9﹣m2≤0,m>0,若q是p的必要不充分条件,求m的取值范围.24.已知椭圆C: +=1(a>b>0)的一个焦点(﹣3,0),离心率e=(1)求椭圆C的方程;(2)求过点(3,0)且斜率为l的直线被椭圆C所截线段得中点坐标.2017-2018学年陕西省咸阳市三原县北城中学高二(上)第三次月考数学试卷(文科)参考答案与试题解析一、选择题(本大题共15小题,每小题5分,满分75分)1.命题“若p则q”的逆命题是()A.若q则p B.若¬p则¬q C.若¬q则¬p D.若p则¬q【考点】四种命题.【分析】将原命题的条件与结论互换,可得逆命题,从而可得【解答】解:将原命题的条件与结论互换,可得逆命题,则命题“若p则q”的逆命题是若q则p.故选A.2.在等差数列{a n}中,a1+a9=10,则a5的值为().A.5 B.6 C.8 D.10【考点】等差数列的通项公式.【分析】本题主要是等差数列的性质等差中项的应用,用求出结果.【解答】解:由等差数列的性质得a1+a9=2a5,∴a5=5.故选A3.命题“对任意x∈R,都有x2≥0”的否定为()A.对任意x∈R,都有x2<0 B.不存在x∈R,都有x2<0C.存在x0∈R,使得x02≥0 D.存在x0∈R,使得x02<0【考点】命题的否定;全称命题.【分析】直接利用全称命题的否定是特称命题,写出命题的否定命题即可.【解答】解:因为全称命题的否定是特称命题,所以命题“对任意x∈R,都有x2≥0”的否定为.存在x0∈R,使得x02<0.故选D.4.设抛物线的顶点在原点,准线方程为x=﹣2,则抛物线的方程是()A.y2=﹣8x B.y2=﹣4x C.y2=8x D.y2=4x【考点】抛物线的简单性质.【分析】根据抛物线的顶点在原点,准线方程为x=﹣2,可设抛物线的方程为y2=2px(p>0),从而可求抛物线的方程.【解答】解:∵抛物线的顶点在原点,准线方程为x=﹣2∴可设抛物线的方程为y2=2px(p>0)∵=2∴2p=8∴抛物线的方程为y2=8x故选C.5.在等比数列{a n}中,a1+a2=2,a3+a4=50,则公比q的值为()A.25 B.5 C.﹣5 D.±5【考点】等比数列的通项公式.【分析】由已知可得:a3+a4=q2(a1+a2)=2q2=50,即可得出.【解答】解:∵a1+a2=2,a3+a4=50,∴a3+a4=q2(a1+a2)=2q2=50,解得q=±5.故选:D.6.“1<x<2”是“x<2”成立的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】设A={x|1<x<2},B={x|x<2},判断集合A,B的包含关系,根据“谁小谁充分,谁大谁必要”的原则,即可得到答案.【解答】解:设A={x|1<x<2},B={x|x<2},∵A⊊B,故“1<x<2”是“x<2”成立的充分不必要条件.故选A.7.若变量x,y满足约束条件,则z=2x+y的最小值为()A.3 B.2 C.1 D.0【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用z的几何意义即可得到结论.【解答】解:设z=2x+y,即y=﹣2x+z作出不等式组对应的平面区域如图:由图象可知当直线y=﹣2x+z过点B(1,0)时,直线y=﹣2x+z的在y轴的截距最小,此时z最小,即z=2+0=2,故选:B.8.在△ABC中,若∠A=60°,∠B=45°,,则AC=()A. B. C.D.【考点】正弦定理.【分析】结合已知,根据正弦定理,可求AC【解答】解:根据正弦定理,,则故选B9.已知命题甲:“任意两个数a,b必有唯一的等差中项”,命题乙:“任意两个数a,b必有两个等比中项”.则()A.甲是真命题,乙是真命题B.甲是真命题,乙是假命题C.甲是假命题,乙是真命题D.甲是假命题,乙是假命题【考点】命题的真假判断与应用.【分析】由题意,可先对命题甲:“任意两个数a,b必有唯一的等差中项”,命题乙:“任意两个数a,b必有两个等比中项”的真假性作出判断,再选出正确选项【解答】解:命题甲:“任意两个数a,b必有唯一的等差中项”,是正确的,因为任意两个数a,b必有唯一的等差中项是,故是正确的;命题乙:“任意两个数a,b必有两个等比中项”是一个假命题,因为若这两个数一正一负,则不能找到它的等比中项,故是错误的.综上知,甲是真命题,乙是假命题故选B10.设a,b,c∈R,且a>b,则()A.ac>bc B.C.a2>b2D.a3>b3【考点】不等关系与不等式.【分析】对于A、B、C可举出反例,对于D利用不等式的基本性质即可判断出.【解答】解:A、3>2,但是3×(﹣1)<2×(﹣1),故A不正确;B、1>﹣2,但是,故B不正确;C、﹣1>﹣2,但是(﹣1)2<(﹣2)2,故C不正确;D、∵a>b,∴a3>b3,成立,故D正确.故选:D.11.已知双曲线﹣=1的右焦点为(3,0),则该双曲线的离心率等于()A.B.C.D.【考点】双曲线的简单性质.【分析】根据双曲线﹣=1的右焦点为(3,0),可得a=2,进而可求双曲线的离心率.【解答】解:∵双曲线﹣=1的右焦点为(3,0),∴a2+5=9∴a2=4∴a=2∵c=3∴故选C.12.过点(﹣3,2)且与=1有相同焦点的椭圆的方程是()A.=1 B.=1C.=1 D.=1【考点】椭圆的标准方程.【分析】求出椭圆的焦点坐标,利用椭圆的定义,求出a,c,然后求出b,即可得到结果【解答】解:由题意=1的焦点坐标(),所以2a==2,所以a=.所以b2=15﹣5=10所以所求椭圆的方程为:=1.故选A.13.下列函数中,最小值为4的是()A.y=x+B.y=sinx+(0<x<π)C.y=e x+4e﹣x D.y=+【考点】基本不等式.【分析】在A中,当x<0时,≤﹣2=﹣4;在B中,由sinx≤1,知y=sinx+≥2=4不正确;在C中,y=e x+4e﹣x≥2=4;在D中,当x=0时,y=<4.【解答】解:在A中,当x>0时,≥2=4;当x<0时,≤﹣2=﹣4.故A错误;在B中,当0<x<π,y=sinx+≥2=4,当且仅当sinx=2时取等号,由sinx≤1,知B不正确;在C中,y=e x+4e﹣x≥2=4,当且仅当e x=4e﹣x,即e x=2时,取最小值,故C正确;在D中,当x=0时,y=+==<4,故D错误.故选:C.14.若2x+2y=1,则x+y的取值范围是()A.[0,2]B.[﹣2,0] C.[﹣2,+∞)D.(﹣∞,﹣2]【考点】基本不等式.【分析】根据指数式的运算性质结合基本不等式可把条件转化为关于x+y的不等关系式,进而可求出x+y的取值范围.【解答】解:∵1=2x+2y≥2•(2x2y),变形为2x+y≤,即x+y≤﹣2,当且仅当x=y时取等号.则x+y的取值范围是(﹣∞,﹣2].故选D.15.关于x的不等式x2﹣2ax﹣8a2<0(a>0)的解集为(x1,x2),且:x2﹣x1=15,则a=()A.B.C.D.【考点】一元二次不等式的解法.【分析】利用不等式的解集以及韦达定理得到两根关系式,然后与已知条件化简求解a的值即可.【解答】解:因为关于x的不等式x2﹣2ax﹣8a2<0(a>0)的解集为(x1,x2),所以x1+x2=2a…①,x1•x2=﹣8a2…②,又x2﹣x1=15…③,①2﹣4×②可得(x2﹣x1)2=36a2,代入③可得,152=36a2,解得a==,因为a>0,所以a=.故选:A.二、填空题:(本大题共5小题,每小题5分,共25分)16.三角形的一边长为14,这条边所对的角为60°,另两边之比为8:5,则这个三角形的面积为.【考点】三角形中的几何计算.【分析】设另两边分别为8k 和5k,由余弦定理可求得k=2,故另两边分别为16和10,故这个三角形的面积为×16×10sin60°,计算求得结果.【解答】解:设另两边分别为8k 和5k,由余弦定理可得142=64k2+25k2﹣80k2cos60°,∴k=2,故另两边分别为16和10,故这个三角形的面积为×16×10sin60°=,故答案为:.17.过双曲线左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是28.【考点】双曲线的简单性质.【分析】由双曲线方程求得a=4,由双曲线的定义可得AF2+BF2=22,△ABF2的周长是(AF1+AF2)+(BF1+BF2)=(AF2+BF2)+AB,计算可得答案.【解答】解:由双曲线的标准方程可得a=4,由双曲线的定义可得:AF2﹣AF1=2a,BF2﹣BF1=2a,∴AF2+BF2﹣AB=4a=16,即AF2+BF2﹣6=16,AF2+BF2=22.△ABF2(F2为右焦点)的周长是:(AF1+AF2)+(BF1+BF2)=(AF2+BF2)+AB=22+6=28.故答案为:28.18.对于任意实数x,不等式ax2﹣2x﹣4<0恒成立,则实数a的取值范围是(﹣,.【考点】函数恒成立问题.【分析】根据不等式恒成立的条件,建立条件关系即可得到结论.【解答】解:当a=0时,不等式等价为﹣4<0,满足条件.若a≠0,则要使不等式ax2﹣2x﹣4<0恒成立,则满足,即,∴解得﹣<a<0,综上:a的取值范围(﹣,0],故答案为:(﹣,0]19.点P是抛物线y2=4x上一动点,则点P到点(0,﹣1)的距离与到抛物线准线的距离之和的最小值是.【考点】抛物线的简单性质;点到直线的距离公式.【分析】先求出抛物线的焦点坐标,再由抛物线的定义可得d=|PF|+|PA|≥|AF|,再求出|AF|的值即可.【解答】解:依题设P在抛物线准线的投影为P',抛物线的焦点为F,A(0,﹣1).则F(1,0),依抛物线的定义知P到该抛物线准线的距离为|PP'|=|PF|,则点P到点A(0,﹣1)的距离与P到该抛物线准线的距离之和,d=|PF|+|PA|≥|AF|==.故答案为:.20.已知命题P:不等式<0的解集为{x|0<x<1};命题q:在△ABC中,“A>B”是“sinA>sinB”成立的必要不充分条件.有下列四个结论:①p真q假;②“p∧q”为真;③“p∨q”为真;④p假q真其中正确结论的序号是①③.(请把正确结论的序号都填上)【考点】命题的真假判断与应用;复合命题的真假.【分析】由题意判断命题P是不是真命题,命题q是不是真命题,即可判断正确选项.【解答】解:命题P:不等式<0⇔x(x﹣1)<0,故不等式<0的解集为{x|0<x<1},故p为真命题;命题q:∵sinA>sinB由正弦定理可得a 2R>b 2R∴a>b⇒A>B即sinA>sinB⇒A>B若A>B①若90°≥A>B,则y=sinx在(0°,90°]单调递增,从而可得sinA>sinB②若A>90°>B,则0°<180°﹣A<90°.∵A+B<180°∴0°<B<180°﹣A<90°∴sin>sinB∴sinA>sinB⇒sinA即A>B⇒sinA>sinB∴A>B”是“sinA>sinB成立的充要条件,故q是假命题故答案为①③三、解答题(本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤)21.已知抛物线的顶点在原点,对称轴为y轴,其上一点A (m,﹣4)到焦点F的距离为6.求抛物线的方程及点A的坐标.【考点】抛物线的简单性质.【分析】由题意可设抛物线的标准方程为:x2=﹣2py(p>0),可得﹣(﹣4)=6,解得p,进而得出抛物线的方程及点A的坐标.【解答】解:由题意可设抛物线的标准方程为:x2=﹣2py(p>0),∵﹣(﹣4)=6,解得p=4.∴抛物线的标准方程为:x2=﹣8y,把点A (m,﹣4)代入可得:m2=﹣8×(﹣4),解得m=±4.∴A(±4,﹣4).22.已知数列{a n}是等差数列,a1=2,a1+a2+a3=12(1)求数列{a n}的通项公式(2)令b n=a n+3n,求{b n}的前n项和.【考点】数列的求和;等差数列的通项公式.【分析】(1)由等差数列的通项公式得2+2+d+2+2d=12,从而求出公差d,由此能求出数列{a n}的通项公式.(2)由b n=a n+3n=2n+3n,利用分组求和法能求出{b n}的前n项和.【解答】解:(1)∵数列{a n}是等差数列,a1=2,a1+a2+a3=12∴2+2+d+2+2d=12,解得d=2,∴数列{a n}的通项公式a n=2+(n﹣1)×2=2n.(2)∵b n=a n+3n=2n+3n,∴{b n}的前n项和:S n=2(1+2+3+…+n)+(3+32+33+…+3n)=+=.23.已知命题P:(1﹣x)(x+4)≥0,q:x2﹣6x+9﹣m2≤0,m>0,若q是p的必要不充分条件,求m的取值范围.【考点】必要条件、充分条件与充要条件的判断.【分析】根据一元二次不等式的解法,分别求出命题p和q,根据q是p的必要不充分条件,可得p⇒q,求出实数m的取值范围;【解答】解:由:(1﹣x)(x+4)≥0,得﹣4≤x≤1;由x2﹣6x+9﹣m2≤0,得3﹣m≤x≤3+m(m>0).由q是p的必要不充分条件,即p⇒q,q推不出p,由p⇒q得,解得m≥7.故m的取值范围是[7,+∞).24.已知椭圆C: +=1(a>b>0)的一个焦点(﹣3,0),离心率e=(1)求椭圆C的方程;(2)求过点(3,0)且斜率为l的直线被椭圆C所截线段得中点坐标.【考点】椭圆的简单性质.【分析】(1)运用椭圆的离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(2)求出直线的方程,代入椭圆方程,运用韦达定理和中点坐标公式,计算即可得到所求中点坐标.【解答】解:(1)由题意可得e==,c=3,可得a=2,b==,即有椭圆方程为+=1;(2)由点(3,0)满足+<1,即(3,0)在椭圆内,设过点(3,0)且斜率为l的直线为y=x﹣3,代入椭圆方程,可得5x2﹣24x+24=0,显然△=242﹣4×5×24>0,设所截线段的端点的坐标为(x1,y1),(x2,y2),可得x1+x2=,由中点坐标公式可得所截线段的中点横坐标为=,纵坐标为﹣3=﹣.即有被椭圆C所截线段的中点坐标为(,﹣).2018年8月2日。
2016—2017学年度第一学期第二次月考高二数学(理)试题一.选择题(共12小题,每小题5分,答案写到答题卡上)1.a ,b ,c ∈R ,则下列命题正确的是( )A .若a 2>b 2,则a >bB .若a <b ,则ac <bcC .若a >b ,则D .若a >c ,b >d ,则a+b >c+d2.函数y=2x+(x >0)的最小值为( )A .2B . 2C . 4D .43.命题5:>x p ,命题3:>x q ,则p 是q 的 ( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件 4.命题:“若a 2+b 2=0(a ,b ∈R ),则a =b =0”的逆否命题是( ) A .若a ≠b ≠0(a ,b ∈R ),则a 2+b 2≠0B .若a =b ≠0(a ,b ∈R ),则a 2+b 2≠0C .若a ≠0且b ≠0(a ,b ∈R ),则a 2+b 2≠0D .若a ≠0或b ≠0(a ,b ∈R ),则a 2+b 2≠05.不等式组⎩⎪⎨⎪⎧ x ≥0,x +3y ≥4,3x +y ≤4,所表示的平面区域的面积等于 ( ) A.32 B.23 C.43 D.346.设a ∈R ,则a >1是1a<1的 ( ) A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分也不必要条件7.如果命题“非p 或非q ”是假命题,则在下列各结论中,正确的是 ( ) ①命题“p 且q ”是真命题 ②命题“p 且q ”是假命题③命题“p 或q ”是真命题 ④命题“p 或q ”是假命题A .①③B .②④C .②③D .①④8. 已知等差数列{a n }满足10,45342=+=+a a a a ,则它的前10项和S 10=( )A.23B.95C.135D.1389.命题p :,x Z ∀∈则240x ->;与命题q :,x Z ∃∈使240x ->,下列结论正确的是( )A .p q 真假B .p q 假真C .p q ∧为真D .p q ∨为假10.已知x , y 满足约束条件,11⎪⎩⎪⎨⎧-≥≤+≤y y x x y y x z +=2则的最大值为( )A .3B .-3C .1D .23 11.对一切实数x ,不等式022<--ax ax 恒成立,则实数a 的取值范围是( )A .[]0,8-B .)0,8(-C .]0,8(-D .[)8,012.要测量底部不能到达的电视塔AB 的高度,在C 点测得塔顶A 的仰角是45°,在D 点测得塔 顶A 的仰角是30°,并测得水平面上的∠BCD =120°,CD =40m,则电视塔的高度为 ( )A .102mB .20mC .203mD .40m 二、填空题:(本大题共4小题,每小题5分,共20分.)13.已知0,0x y >>且满足281x y+=,则x y +的最小值为 14.在ABC ∆中,3,5,120a b C ︒===,则c =___________.15.等差数列{}n a 的公差0d ≠,且358a a a 、、依次成等比数列,则59S a =___ ____. 16.下列说法①.若lg a ,lg b ,lg c 成等差数列,则a ,b ,c 成等比数列②.若命题p :“存在x ∈R ,x 2-x -1>0”,则命题p 的否定为:“对任意x ∈R , x 2-x -1≤0”③.若x ≠0,则x +1x≥2 ④.“a =1”是“直线x -ay =0与直线x +ay =0互相垂直”的充要条件其中正确结论的序号为 (把你认为正确结论的序号都填上).三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本题满分10分) 已知P :方程x 2+mx+1=0有两个不等的实数根,Q :方程4x 2+4(m ﹣2)x+1=0无实根.若P ∨Q 为真,P ∧Q 为假,求实数m 的取值范围.18.(本题满分12分)在等比数列{}n a 中,已知368,64a a ==,(1)求数列{}n a 的通项公式;(2)若2log n n b a =,求数列{}n b 的前n 项和n S .19.(本题满分12分)在锐角ABC ∆中,a b c 、、分别是角A B C 、、2sin c A=,(1)求角C 的大小; (2)若c ABC ∆的面积为,求a b +的值. 20.(本题满分12分)已知函数2()2f x ax bx a =+-+(1)若关于x 的不等式()0f x >的解集是(1,3)-,求实数,a b 的值;(2)若2,0b a =>,解关于x 的不等式()0f x >.21.(本小题满分12分)正方体ABCD -A 1B 1C 1D 1的棱长为1,点F 为A 1D 的中点.(1)证明:A 1B ∥平面AFC ;(2)求二面角B -AF -C 夹角的余弦值.22、(本小题满分12分)如图,在四棱锥O ABCD -中,底面A B C D 是边长为1的菱形,∠ABC=600, OA ABCD ⊥底面, 2OA =,M 为OA 的中点。
陕西省咸阳市2016-2017学年高二数学下学期第一次月考试题 理(无答案)一、选择题(本大题共10小题,每小题5分,满分50分) 1、下面叙述正确的是( )A .综合法、分析法是直接证明的方法B .综合法是直接证法、分析法是间接证法C .综合法、分析法所用语气都是肯定的D .综合法、分析法所用语气都是假定的 2、下面使用类比推理正确的是 ( ). A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =” B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C.“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ (c ≠0)” D.“n n a a b =n (b )” 类推出“n n a a b +=+n(b )”3.当=n 1,2,3,4,5,6时,比较n 2和2n 的大小并猜想 ( )A.1≥n 时,22n n> B. 3≥n 时,22n n> C. 4≥n 时,22n n> D. 5≥n 时,22n n>4. 已知14a b c =+==则a ,b ,c 的大小关系为( ) A .a>b>c B .c>a>b C .c>b>a D .b>c>a5. =∆∆--∆+→∆xx x f x x f 2)()(lim000x ( )A.)(210x f ' B. )(0x f ' C. )(20x f ' D. )(-0x f ' 6.设xx y sin 12-=,则='y ( ).A .x x x x x 22sin cos )1(sin 2---B .x x x x x 22sin cos )1(sin 2-+- C .x x x x sin )1(sin 22-+- D .xx x x sin )1(sin 22---7.下列结论中正确的是( ) A 导数为零的点一定是极值点 B 如果在x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极大值C 如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极小值 D 如果在x 附近的左侧0)('<x f ,右侧0)('>x f ,那么)(0x f 是极大值8. 曲线322+=x y 在点1-=x 处的切线方程为( )A.14+=x yB. 54--=x yC. 14+-=x yD. 54-=x y9.若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象是( )10.在R 上的可导函数c bx ax x x f +++=22131)(23,当)1,0(∈x 取得极大值,当)2,1(∈x 取得极小值,则12--a b 的取值范围是( ). A .)1,41( B .)1,21( C .)41,21(- D .)21,21(-二、填空题(本大题共4小题,每小题4分,满分16分)11.曲线3x y =在点)8,2(处的切线方程为12. “开心辞典”中有这样的问题:给出一组数,要你根据规律填出后面的第几个数,现给出一组数:12 ,-12 ,38 ,-14 ,532,它的第8个数可以是 。
2017--2018学年度第一学期第一次月考高二数学试题一、选择题(本大题共12小题,每小题5分,满分60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.数列3,7,11,…中,第5项为( )A .15B .18C .19D .232.在等比数列中,112a =,12q =,132n a =,则项数n 为( )A. 3B. 4C. 5D. 63.在数列{}n a 中,1a =1,12n n a a +-=,则51a 的值为( )A .99B .49C .102D . 1014.在等差数列{}n a 中,1910a a +=,则5a 的值为( )A.5B.6C.8D.105.,2m n 的等差中项为4,2,m n 的等差中项为5,则,m n 的等差中项为( )A. 2B. 3C. 6D. 96.在等差数列{}n a 中,24)(2)(31310753=++++a a a a a ,则此数列前13项和为( )A .26B .13C .39D .527.设等比数列{a n }中,每项均为正数,且8183=⋅a a ,1032313log log log a a a ++等于( )A.5B.10C.20D.408.一个等比数列}{n a 的前n 项和为48,前2n 项和为60,则前3n 项和为( )A.63B.108C.75D. 839.在各项都为正数的等比数列{}n a 中,首项13a =,前三项和为21,则345a a a ++=( )A.33B.72C.84D.18910.已知1,,921--a a ,成等差数列,1,,,9321--b b b ,成等比数列,则=-)(122a a b ( )A.8B.-8C.±8D.9811.数列{}n a 的前n 项和为n S ,若1(1)n a n n =+,则5S 等于( ) A.1 B.56 C.16 D.13012.若4711310()2222...2n f n +=+++++,则()f n = ( )A .122n +-B .2(81)7n -C .12(81)7n +-D .42(81)7n +- 二、填空题(本大题共4小题,每小题5分,满分20分)13.数列 ,,,666666的一个通项公式为14.在数列{}n a 中,22,111+==+n n n a a a a ,则=4a 15.在数列{}n a 中,其前n 项和S n =3·2n +k ,若数列{}n a 是等比数列,则常数k 的值为16.小明在玩投石子游戏,第一次走1米放2颗石子,第二次走2米放4颗石子…第n 次走n 米放2n颗石子,当小明一共走了36米时,他投放石子的总数是三、解答题(本大题共6小题,满分70分. 解答应写出必要的文字说明、证明过程或推演步骤)17.(本小题满分10分)(1)等差数列{}n a 中,42=a ,,1574=+a a 求通项公式.(2)在等比数列{}n a 中,若422324,6,a a a a -=+=求公比q .18.(本小题满分10分)已知n S 为数列{}n a 的前n 项和,若31n n S =+,求{}n a 的通项公式19.(本小题满分12分)已知数列{}n a 满足)(12,111*+∈+==N n a a a n n(1)求证:数列}1{+n a 是等比数列;(2)求通项公式n a ;20. (本小题满分12分)等差数列{}n a 的前n 项和为n n S n 2052+-=,求数列{}n a 的前n 项和n S21. (本小题满分13分)设数列{}n a 前n 项和为n S , 满足 121+=n n s a (*∈N n ). (1)求数列{}n a 的通项公式;(2)令,nn b na = 求数列{}n b 的前n 项和n T ; .22. (本小题满分13分)设{}n a 是等差数列,{}n b 是各项都为正数的等比数列,且111==b a ,2153=+b a ,1335=+b a(1)求{}n a ,{}n b 的通项公式;(2)求数列{}n n b a +的前n 项和n S。
2017-2018学年陕西省咸阳市三原县北城中学高二(下)第一次月
考数学试卷(文科)
一、选择题:(每小题5分共60分)
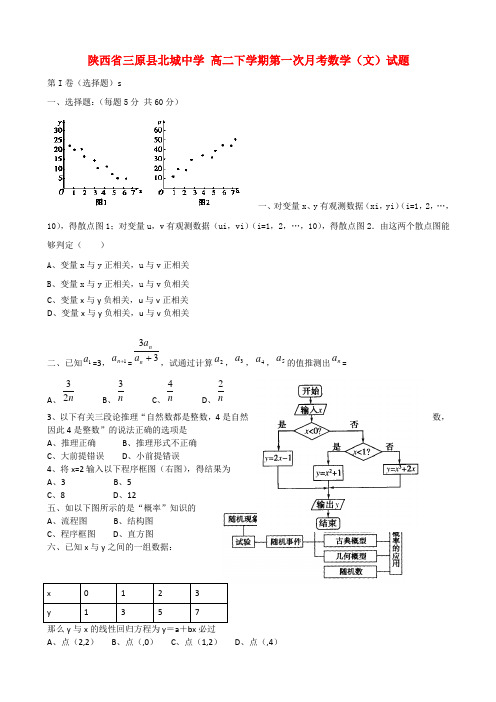
1.对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
2.已知a1=3,a n+1=,试通过计算a2,a3,a4,a5的值推测出a n=()
A.B.C.D.
3.下列有关三段论推理“自然数都是整数,4是自然数,所以4是整数”的说法正确的是()A.推理正确B.推理形式不正确
C.大前提错误D.小前提错误
4.将x=2输入以下程序框图(如图),得结果为()
A.3 B.5 C.8 D.12
5.如图所示的是“概率”知识的()
A.流程图B.结构图C.程序框图D.直方图
6.已知x与y之间的一组数据如表,则y与x的线性回归方程=x+必过()
x 0 1 2 3
y 1 3 5 7
A.点(2,2)B.点(1.5,0)C.点(1,2)D.点(1.5,4)
7.给出下列五个:
①净A,B,C三种个体按3:1:2的比例分层抽样调查,如果抽取的A个体为9个,则样本容易为30;
②一组数据1、2、3、4、5的平均数、众数、中位数相同;
③甲组数据的方差为5,乙组数据为5、6、9、10、5,那么这两组数据中较稳定的是甲;
④已知具有线性相关关系的两个变量满足的回归直线方程为y=1﹣2x.则x每增加1个单位,y平均减少2个单位;
⑤统计的10个样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在,(2,4],(4,6],(6,8],(8,10],(10,12],估计该校学生每周平均体育运动时间超过4小时的概率;
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
P(K2≥k0)0.10 0.05 0.010 0.005
k0 2.706 3.841 6.635 7.879
附:K2=.
2014-2015学年陕西省咸阳市三原县北城中学高二(下)
第一次月考数学试卷(文科)
参考答案与试题解析
一、选择题:(每小题5分共60分)
1.对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
考点:散点图.
专题:数形结合法.
分析:通过观察散点图可以知道,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.
解答:解:由题图1可知,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,
由题图2可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.
故选C
点评:本题考查散点图,是通过读图来解决问题,考查读图能力,是一个基础题,本题可以粗略的反应两个变量之间的关系,是不是线性相关,是正相关还是负相关.
2.已知a1=3,a n+1=,试通过计算a2,a3,a4,a5的值推测出a n=()
A.B.C.D.
考点:数列递推式.
专题:点列、递归数列与数学归纳法.
分析:由已知结合递推式依次求得算a2,a3,a4,a5,寻找规律后得答案.
解答:解:由a1=3,a n+1=,得
,
,
,
.
右上可知,.
故选:D.
点评:本题考查了数列递推式,关键是发现规律,是基础题.
3.下列有关三段论推理“自然数都是整数,4是自然数,所以4是整数”的说法正确的是()A.推理正确B.推理形式不正确
C.大前提错误D.小前提错误
考点:演绎推理的基本方法.
专题:推理和证明.
分析:要分析一个演绎推理是否正确,主要观察所给的大前提,小前提和结论是否都正确,根据三个方面都正确,得到结论.
解答:解:凡自然数都是整数,而4是自然数,所以4是整数.
大前提:“凡自然数都是整数”是正确的,
小前提:“4是自然数”也是正确的,
结论:“4是整数”是正确的,
∴这个推理是正确的,
故选:A.
点评:本题是一个简单的演绎推理,这种问题不用进行运算,只要根据所学的知识点,判断这种说法是否正确,是一个基础题.
4.将x=2输入以下程序框图(如图),得结果为()
A.3 B.5 C.8 D.12
考点:程序框图.
专题:图表型;算法和程序框图.
分析:模拟程序框图的运行过程,得出该程序的运行结果是计算分段函数f(x)的值;从而求出结果.
解答:解:模拟程序框图的运行过程,知该程序的运行结果是计算分段函数f(x)
=的值;
∴当x=2时,f(x)=23+2×2=12.
故选:D.
点评:本题考查了程序框图与分段函数的应用问题,解题时应模拟程序框图的运行过程,得出程序运行的结果,属于基础题.
5.如图所示的是“概率”知识的()
A.流程图B.结构图C.程序框图D.直方图
考点:结构图.
专题:算法和程序框图.
分析:根据结构图的定义即可得到结论.
解答:解:本图象是显示知识点关系的图表,为结构图,
故选:B
点评:本题主要考查结构图的识别,比较基础.
6.已知x与y之间的一组数据如表,则y与x的线性回归方程=x+必过()
x 0 1 2 3
y 1 3 5 7
A.点(2,2)B.点(1.5,0)C.点(1,2)D.点(1.5,4)
考点:变量间的相关关系.
专题:计算题.
分析:本题是一个线性回归方程,这条直线的方程过这组数据的样本中心点,因此计算这组数据的样本中心点,做出x和y的平均数,得到结果.
解答:解:由题意知,y与x的线性回归方程=x+必过样本中心点,
==1.5,==4,
∵=x+=x+(﹣=(x﹣)+,
∴线性回归方程必过(1.5,4).
故选D
点评:一组具有相关关系的变量的数据(x,y),通过散点图可观察出所有数据点都分布在一条直线附近,这样的直线可以画出许多条,而其中的一条能最好地反映x与y之间的关系,即这条直线“最贴近”已知的数据点,这就是回归直线.
7.给出下列五个:
①净A,B,C三种个体按3:1:2的比例分层抽样调查,如果抽取的A个体为9个,则样本容易为30;
②一组数据1、2、3、4、5的平均数、众数、中位数相同;
③甲组数据的方差为5,乙组数据为5、6、9、10、5,那么这两组数据中较稳定的是甲;
④已知具有线性相关关系的两个变量满足的回归直线方程为y=1﹣2x.则x每增加1个单位,y平均减少2个单位;
⑤统计的10个样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在,(2,4],(4,6],(6,8],(8,10],(10,12],估计该校学生每周平均体育运动时间超过4小时的概率;
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
P(K2≥k0)0.10 0.05 0.010 0.005
k0 2.706 3.841 6.635 7.879
附:K2=.
考点:独立性检验;频率分布直方图.
专题:应用题;概率与统计.
分析:(Ⅰ)根据15000人,其中男生10500人,女生4500人,可得应收集多少位女生的样本数据;
(Ⅱ)由频率分布直方图可得1﹣2×(0.100+0.025)=0.75,即可求出该校学生每周平均体育运动时间超过4小时的概率;
(Ⅲ)写出2×2列联表,求出K2,与临界值比较,即可得出结论.
解答:解:(Ⅰ)300×=90,∴应收集90位女生的样本数据;
(Ⅱ)由频率分布直方图可得1﹣2×(0.100+0.025)=0.75,
∴该校学生每周平均体育运动时间超过4小时的概率为0.75;
(Ⅲ)由(Ⅱ)知,300位学生中有300×0.75=225人每周平均体育运动时间超过4小时,75人每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
男生女生总计
每周平均体育运动时间不超过4小时45 30 75
每周平均体育运动时间超过4小时165 60 225
总计210 90 300
∴K2=≈4.762>3.841,
∴有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
点评:本题主要考查独立性检验等基础知识,考查数形结合能力、运算求解能力以及应用用意识,考查必然与或然思想等,属于中档题.。