第六章_序列相关
- 格式:ppt
- 大小:2.08 MB
- 文档页数:116


第六章动态数列一、判断题二、1.若将某地区社会商品库存额按时间先后顺序排列,此种动态数列属于时期数列。
()三、2.定基发展速度反映了现象在一定时期内发展的总速度,环比发展速度反映了现象比前一期的增长程度。
()四、3.平均增长速度不是根据各期环比增长速度直接求得的,而是根据平均发展速度计算的。
()五、4.用水平法计算的平均发展速度只取决于最初发展水平和最末发展水平,与中间各期发展水平无关。
()六、5.平均发展速度是环比发展速度的平均数,也是一种序时平均数。
()1、×2、×3、√4、√5、√。
七、单项选择题八、1.根据时期数列计算序时平均数应采用()。
九、 A.几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法十、2.下列数列中哪一个属于动态数列()。
AHA12GAGGAGAGGAFFFFAFAF十一、 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列十二、 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列十三、 3.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为()。
十四、十五、AHA12GAGGAGAGGAFFFFAFAF4.说明现象在较长时期内发展的总速度的指标是()。
A、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度5.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为()。
A.(102%×105%×108%×107%)-100%B.102%×105%×108%×107%C.2%×5%×8%×7%D.(2%×5%×8%×7%)-100%6.定基增长速度与环比增长速度的关系是()。

第六章 自相关一、判断题1. 模型中的解释变量含有滞后被解释变量的时候可以使用DW 检验法检验自相关。
(F )2. 可以作残差对某个解释变量的散点图来大概判断是否存在自相关。
(F )3. 存在序列相关时, 使用标准公式估计的随机扰动项的方差不再具有无偏性。
(T )4. 杜宾—瓦尔森检验能够检验出任何形式的自相关。
( F )5. 不存在负的自相关关系。
(F )6. LM 检验与DW 检验结果不一致是很有可能的。
(T )二、存在序列相关时, 有可能会高估或者低估随机扰动项的真实方差, 但通常会低估。
(T )三、单项选择题1. 如果模型存在序列相关, 则( D )。
A......B....C......D.2. DW 检验的零假设是(为随机误差项的一阶相关系数)( B )。
A. DW =0B.C. DW =1D.3.下列哪个序列相关可用DW 检验(为具有零均值, 常数方差且不存在序列相关的随机变量)( A )。
A. B.C.4. DW 的取值范围是( D )。
A. -1≤DW ≤0B. -1≤DW ≤1C. -2≤DW ≤2D. 0≤DW ≤45.当DW =4时, 说明( D )。
A. 不存在序列相关B. 不能判断是否存在自相关C. 存在完全的正的自相关D. 存在完全的负的自相关6.根据20个观测值估计的结果, 一元线性回归模型的DW =2.3。
在样本容量n=20,解释变量k=1, 显著性水平为0.05时, 查得dL=1,dU=1.41,则可以决断( A )。
A. 不存在自相关B. 存在正的自相关C. 存在负的自相关D. 无法确定7.当模型存在序列相关现象时, 适宜的参数估计方法是( C )。
A. 加权最小二乘法B. 间接最小二乘法C. 广义差分法D. 工具变量法8.对于原模型, 广义差分模型是指( D )。
A.B.C.D .()()()1t t 1t t 101t t u u x x 1y y ----+-+-=-ρρβρβρ9. 假定某企业的生产决策是由模型描述的(其中为产量, 为价格), 又知: 如果该企业在t -1期生产过剩, 经营人员会削减t 期的产量。

自相关性一、单项选择题1、如果模型t t t u X b b Y ++=10存在序列相关,则【 】A cov (t x ,t u )=0B cov (t u ,s u )=0(ts )C cov (t x ,t u )0D cov (t u ,s u )0(ts ) 2、DW 检验的零假设是(为随机项的一阶自相关系数)【 】A DW=0B =0C DW=1D =13、下列哪种形式的序列相关可用DW 统计量来检验(i v 为具有零均值,常数方差,且不存在序列相关的随机变量)【 】A t t t v u u +=-1ρB t t t t v u u u +++=--Λ221ρρC t t v u ρ=D Λ++=-12t t t v v u ρρ4、DW 值的取值范围是【 】A -1DW0B -1DW1C -2DW2D 0 DW4 5、当DW =4是时,说明【 】A 不存在序列相关B 不能判断是否存在一阶自相关C 存在完全的正的一阶自相关D 存在完全的负的一阶自相关6、根据20个观测值估计的结果,一元线性回归模型的DW =。
在样本容量n=20,解释变量k=1,显着性水平=时,查得L d =1,U d =,则可以判断【 】A 不存在一阶自相关B 存在正的一阶自相关C 存在负的一阶自相关D 无法确定 7、当模型存在序列相关现象时,适宜的参数估计方法是【 】A 加权最小二乘法B 间接最小二乘法C 广义差分法D 工具变量法 8、对于原模型t t t u X b b Y ++=10,一阶广义差分模型是指【 】A)()()(1)(1t t t t t t t X f u X f X b X f b X f Y ++=B tt t u X b Y ∆+∆=∆1C t t t u X b b Y ∆+∆+=∆10D )()()1(11101----+-+-=-t t t t t t u u X X b b Y Y ρρρρ9、采用一阶差分模型克服一阶线性自相关问题适用于下列哪种情况【 】 A 0 B 1 C -1<<0 D 0<<110、假定某企业的生产决策由模型t t t u P b b S ++=10描述(其中t S 为产量,t P 为价格),如果该企业在t-1期生产过剩,经济人员会削减t 期的产量。





第六章DNA序列分析[本章摘要]DNA 的序列分析有两种基本方法, Maxam-Gilbert 化学降解法和 Sanger 氏酶学法。
因为测序每个反应读取的序列是有限的,做长片段 DNA 或基因组测序时,需要选用一定的策略。
测序的策略有 primer walking ,随机测序,定向测序等。
现在全自动测序仍然沿用 Sanger 氏酶学法,但是在标记上作了改进。
DNA 测序结果通过生物信息学分析,获取需要的信息。
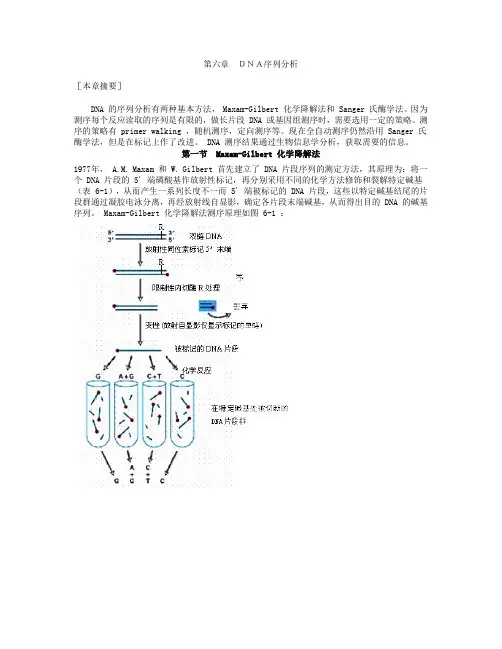
第一节Maxam-Gilbert 化学降解法1977年, A.M. Maxam 和 W. Gilbert 首先建立了 DNA 片段序列的测定方法,其原理为:将一个 DNA 片段的 5' 端磷酸基作放射性标记,再分别采用不同的化学方法修饰和裂解特定碱基(表 6-1),从而产生一系列长度不一而 5' 端被标记的 DNA 片段,这些以特定碱基结尾的片段群通过凝胶电泳分离,再经放射线自显影,确定各片段末端碱基,从而得出目的 DNA 的碱基序列。
Maxam-Gilbert 化学降解法测序原理如图 6-1 :表6-1:Maxam-Gilbert化学降解法测序的常用化学试剂:碱基体系化学修饰试剂化学反应断裂部位GA + G C + T CA > C dimethyl sulphate(硫酸二甲酯)Piperidine formate(哌啶甲酸), pH2.0hydrazine(肼,联氨NH2.NH2)hydrazine + NaCl(1.5M)90 C, NaOH(1.2M)甲基化脱嘌呤打开嘧啶环打开胞嘧啶环断裂反应GG和AC和TCA和C硫酸二甲酯[dimethyl sulphate ,DMS ,(CH3O)2SO2]是一种碱性化学试剂,可以使 DNA 链上的腺嘌呤 A 的 N2和鸟嘌呤 G 的 N7甲基化,但是鸟嘌呤 G 的 N7甲基化速度比腺嘌呤 A 的 N2甲基化速度要快 4-10 倍,并且在中性 pH 环境中, DMS 主要作用于鸟嘌呤 G ,使之甲基化,导致糖苷键断裂。