下载文档原格式
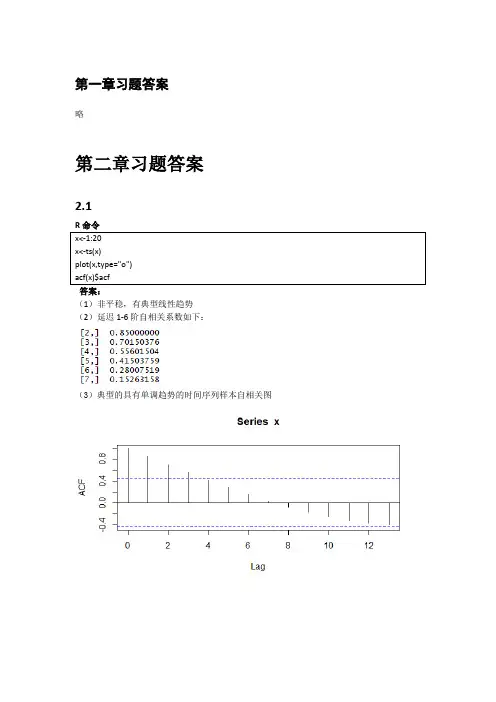
第一章习题答案略第二章习题答案2.1答案：（1）非平稳，有典型线性趋势（2）延迟1-6阶自相关系数如下：（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）1-24阶自相关系数如下（3）自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案：我们自定义函数，计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。
2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11（2）差分序列平稳，非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。
第七章时间数列分析一、填空题1、时间指标数值2、逐期增长量累计增长量3、增长水平（或增长量）发展速度4、本期水平去年同期水平5、年距发展速度 1（或100%）6、几何平均法方程法7、同季（月）平均法趋势与季节模型法8、平均季节比重法平均季节比率法9、报告期水平基期水平10、序时平均数（或动态平均数）平均数11、和差12、季节变动长期趋势13、逐期增长量环比增长速度14、长明显1-5 A C C A D 6-10 A B A D B三、多选题1、CDE2、ABDE3、ABCE4、ACDE5、BDE6、BD7、ABCD8、ACE9、AE 10、ACE四、简答题1、序时平均数与一般平均数的异同。
答：（1）相同之处。
二者都是将具体数值抽象化，用一个代表性的数指来代表总体的一般水平。
（2）不同之处。
①计算的依据不同。
一般平均数是根据变量数列计算的，而序时平均数则是根据时间数列计算的；②对比的指标不同。
一般平均数是总体标志总量与总体单位总量对比的结果，而序时平均数则是时间数列各期发展水平的总和与时期项数对比的结果；③说明的问题不同。
一般平均数说明现象在同一时间、不同空间上所达到的一般水平，而序时平均数则说明现象在同一空间、不同时间上所达到的一般水平。
2、时期数列与时点数列的区别。
答：①时期数列中的指标值为时期数，时点数列中的指标值为时点数；②时期数列中的指标值具有可加性，而时点数列中的指标值则不具有可加性；③时期数列中指标值的大小与时间间隔的长短有直接关系，而时点数列中指标值的大小与时间间隔的长短则没有直接关系；④时期数列中的指标值是通过连续调查取得的，而时点数列中的指标值则是通过一次性调查取得的。
3、时间数列的编制原则。
答：（1）基本原则：保持数列中的各项指标数值具有可比性。
（2）具体原则：①时间长短统一；②总体范围统一；③指标口径统一；④计算方法统一；⑤计量单位统一。
4、计算和应用平均速度应注意的问题。
序列数据的特征提取方法及在基因组学研究方面的应用分析引言：基因组学是研究生物体基因组结构、功能和调控的学科，其中序列数据的处理与分析是关键的一环。
随着高通量测序技术的不断发展，获取到的序列数据呈现急剧增加的趋势。
如何从庞大的序列数据中提取有用的特征信息并进行深入的分析成为了基因组学研究领域中的重要课题。
本文将介绍序列数据的特征提取方法，并重点探讨其在基因组学研究方面的应用和意义。
一、序列数据的特征提取方法1.1 k-mer特征：k-mer是指序列中连续k个碱基的组合。
k-mer特征提取是一种广泛应用于基因组学研究的方法。
通过统计序列中所有可能的k-mer的出现频率，可以得到一个特定长度的特征向量。
这些特征向量可以用于比较和分类不同的生物组织、物种或环境。
k-mer特征提取方法简单高效，可应用于多种序列数据类型，如基因序列、转录组数据、代谢组数据等。
1.2 Motif特征：Motif是指在DNA或蛋白质序列中的重复模式或保守序列。
Motif特征提取是一种常用于分析基因组和蛋白质序列的方法。
通过使用计算机算法和模式识别技术，可以从序列数据中提取出具有生物学意义的Motif。
Motif特征在识别转录因子结合位点、预测启动子和剪接位点等方面起着重要作用。
1.3 突变特征：突变是指基因组中发生的DNA序列的变化。
突变特征提取是一种用于鉴定和分析基因组变异的方法。
通过比较多个个体或物种的序列数据，可以发现其中存在的突变。
突变特征对于研究个体之间的差异以及相关疾病的遗传基础具有重要的意义。
二、序列数据特征提取方法在基因组学研究中的应用2.1 基因表达谱的分析：基因表达谱是指在特定条件下基因表达的水平。
通过对转录组数据的特征提取，可以得到不同基因的表达模式，从而揭示基因在不同生理和病理过程中的功能。
例如，通过对肿瘤组织和正常组织的转录组数据进行特征提取和比较，可以发现与癌症相关的基因。
2.2 DNA甲基化的分析：DNA甲基化是指DNA分子上的甲基基团添加或拆除的过程，对基因的转录和表达有重要影响。
时间序列的分解分析一、时间序列分解分析的原理时间序列分解分析的原理是基于时间序列数据的两个基本特征：长期趋势和短期季节变动。
长期趋势是指时间序列数据在长期内呈现的整体上升或下降趋势，而短期季节变动则是指时间序列数据在每个季节内的周期性变动。
时间序列分解分析将时间序列数据分解成长期趋势、季节性、循环和随机成分，以便更好地理解和分析时间序列数据。
二、时间序列分解分析的步骤时间序列分解分析的步骤通常包括以下几个步骤：数据获取、数据处理、分解分析、模型建立和预测。
1. 数据获取：从相应的数据源获取需要分析的时间序列数据。
对于涉及的时间序列数据，通常需要有一定的历史数据，以便进行分析和建模。
2. 数据处理：对获取的时间序列数据进行数据处理，例如数据清洗、缺失值填补、异常值处理等。
这一步骤的目的是确保数据的准确性和完整性。
3. 分解分析：对经过数据处理的时间序列数据进行分解分析。
通常使用的方法有移动平均法、指数平滑法和加法模型等。
这些方法可以将时间序列数据分解成长期趋势、季节性、循环和随机成分。
4. 模型建立：基于分解分析的结果，建立合适的模型。
常用的模型有ARIMA模型、指数平滑模型、回归分析等。
模型的选择需要根据具体的时间序列数据和分析目的来确定。
5. 预测：利用建立的模型对未来的时间序列数据进行预测。
根据建立的模型，可以得到未来一段时间内的长期趋势、季节性、循环和随机成分的预测值，从而提供决策参考。
三、实例分析为了更好地理解时间序列分解分析的步骤和应用，我们以某公司销售额数据为例进行分析。
假设该公司的销售额数据具有长期增长趋势和季节性变动。
1. 数据获取：从公司的销售系统中获取过去几年的销售额数据，包括每个月的销售额。
2. 数据处理：对获取的销售额数据进行数据清洗，排除异常值和缺失值。
3. 分解分析：利用加法模型对销售额数据进行分解分析。
加法模型将销售额数据分解成长期趋势、季节性、循环和随机成分。
通过分析过去几年的销售额数据，可以得到相应的分解结果。
特征分解和奇异值分解的真正意义特征分解和奇异值分解在机器学习的应用中经常出现，在学习线性代数的时候也学习过。
线性代数学完之后，之后去按照步骤去求解特征值和特征向量，也没搞明白特征值和特征向量究竟有什么作用。
这篇文章的主要内容包括：1、什么是特征分解2、什么是奇异值分解3、如何求解特征值和特征向量4、特征值和特征向量有什么意义一、特征分解特征分解(eigendecomposition)：是使用最广的矩阵分解之一，通过特征分解可以将矩阵分解成一组特征值和特征向量。
方阵A的特征向量(eigenvector)是指与A相乘后相当于对该向量进行缩放的非零向量v其中v就是方阵A的特征向量，λ就是A的特征值。
如果v是A 的特征向量，那么任何缩放后的向量s*v(s为任意实数，且不为0)也是A的特征向量。
同时sv和v具有相同的特征值。
所以，通常情况下我们都只考虑单位特征向量。
通过将矩阵分解成为特征值和特征向量，来帮助我们分析矩阵。
二、奇异值分解奇异值分解(singular value decomposition,SVD)：是将矩阵分解成为特征值和特征向量的另一种方法，通过奇异值分解，可以将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。
通过奇异值分解，我们可以得到一些与特征分解相同类型的信息。
而且，奇异值分解的应用非常广泛，如推荐系统、图片压缩等。
每一个实数矩阵都有一个奇异值分解，但不一定有特征分解。
非方阵的矩阵没有特征分解，此时我们只能使用奇异值分解。
奇异值分解，可以将矩阵A分成三个矩阵的乘积：假设A是一个m×n的矩阵，那么U是一个m×m的矩阵，D是一个m×n的矩阵，V是一个n×n的矩阵。
其中，矩阵U和V都是正交矩阵，而矩阵D是对角矩阵。
矩阵D不一定是方阵。
对角矩阵D对角线上的元素就是矩阵A的奇异值(singular value)。
核酸序列特征分析核酸序列特征分析是生物信息学研究中重要的一个方面。
它可以帮助我们更深入地理解基因组及基因表达研究。
本文旨在介绍核酸序列特征分析，其中包括核酸序列分析、核酸序列特征抽取和质粒抽取等内容。
首先，介绍核酸序列分析，其中包括特征分类、序列特征检测、序列分类和序列比对等。
核酸特征分类是将核酸序列分为有用的和无用的，从而排除噪声。
核酸序列特征检测包括对不同类型的基因、基因组表达、基因功能和结构等特征的检测，以及比较不同物种序列或不同基因组结构的检测。
核酸序列分类是用特征抽取技术分析序列长度，以确定序列的分类及特征。
序列比对是比较两个或多个序列的相似性，以发现可能的相似性或共同特征。
其次，介绍核酸序列特征抽取。
它分为特征抽取和质粒抽取两大类。
特征抽取的主要目的是抽取出序列的非特定特征，比如k-mer特征，基于序列单位的反向字典学习（RLD）等方法。
质粒抽取的目的是抽取出序列以及其表达周围的特定特征，比如突变、位点突变、基因连接等。
特征抽取是对序列的概括，抽取出重要的特征，而质粒抽取是对序列表达的概括，可以捕捉到序列的精细结构信息。
最后，介绍核酸序列特征分析的一些应用。
一方面，核酸序列特征分析可以用于揭示基因组结构和功能特征。
例如，可以利用序列比对技术对不同物种序列进行对比，揭示出不同物种的关键基因。
另一方面，核酸序列特征分析也可以用于揭示表达调控机制。
例如，可以用特征分类和序列特征抽取技术，结合表达评价结果，探索基因表达调控的内在机制。
综上所述，核酸序列特征分析是生物信息学研究中重要的一个方面。
它可以用来探索基因组结构和功能特征，揭示表达调控机制，改进基因调控机制，为临床实验提供分析指导，并帮助我们更加深入地了解基因组研究和基因表达研究。
因此，核酸序列特征分析的研究将给生物信息学领域带来许多新的机会。
生物信息学讲义——序列特征分析生物信息学是一门应用生物学、计算机科学和统计学等多学科知识的交叉学科。
其中，序列特征分析是生物信息学中的一个重要研究领域。
它涉及到对生物学序列的各类特征进行提取、分析和解释的过程，可以用于从序列数据中推断生物功能、结构和进化等信息。
序列特征分析的首要任务是对生物学序列进行特征提取。
常见的生物学序列包括DNA序列、RNA序列和蛋白质序列等。
这些序列通常以一串字符的形式保存，比如以“A”、“T”、“G”、“C”表示DNA序列中的碱基。
通过使用序列分析工具，可以将这些字符转化为序列特征的数值表示，以方便后续的计算和分析。
在序列特征分析中，常用的特征包括序列长度、碱基或氨基酸组成、序列重复性、序列保守性、二级结构等。
其中，序列长度是最基本的特征，可以直接从序列中读取得到。
碱基或氨基酸组成是指序列中各类碱基或氨基酸的相对含量。
序列重复性是指序列中出现的重复单元的种类和数量。
序列保守性是指序列在不同物种或不同基因中的保守程度，用于推断序列的功能和进化关系。
二级结构是指蛋白质序列中各个氨基酸的空间排列方式，用于推断蛋白质的结构和功能。
在实际应用中，序列特征分析可以帮助研究人员理解生物系统的结构和功能。
例如，通过分析DNA序列中的启动子、编码区和调控元件等特征，可以推断基因的结构和转录调控机制。
通过分析蛋白质序列中的保守模体和功能域等特征，可以推断蛋白质的功能和进化关系。
通过分析RNA序列的二级结构和稳定性等特征，可以推断RNA的折叠方式和功能。
为了完成序列特征分析的任务，研究人员通常会借助各种生物信息学工具和算法。
比如，BLAST（Basic Local Alignment Search Tool）是一种常用的序列比对工具，可以通过比对已知序列库中的序列，从而推断未知序列的一些特征和功能。
HMM（Hidden Markov Model）是一种常用的序列模型，可以用于推断未知蛋白质序列的二级结构和功能。
