2019年人教版初中七年级数学上册第四章 几何图形初步周周测3(全章)

人教版七年级上册第四章《几何图形初步》单元测试（解析版）一、选择题1、如图所示，该几何体的主视图是（）A． B． C． D．2、图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能围成正方体的位置是（）A．① B．② C．③ D．④3、已知一个几何体的三种视图如图所示，则这个几何体是（）A．圆柱 B．圆锥 C．球体 D．正方体4、下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程，其中可用公理“两点之间，线段最短”来解释的现象有( )A．①② B．①③ C．②④ D．③④5、已知∠AOB＝30°，自∠AOB顶点O引射线OC，若∠AOC︰∠AOB＝4︰3，那么∠BOC的度数是（）A．10° B．40° C．70° D．10°或70°6、．下列说法正确的是（）A．两点之间的连线中，直线最短 B．若P是线段AB的中点，则AP=BPC．若AP=BP，则P是线段AB的中点 D．若A，B，C在同一直线上，且AB=2，BC=3，则AC=57、如图，C，D是线段AB上两点．若CB=4cm，DB=7cm，且D是AC的中点，则AC的长等于（）A．3cm B．6cm C．11cm D．14cm8、如图，下列说法中错误的是（）A．OA的方向是东北方向 B．OB的方向是北偏西60°C．OC的方向是南偏西60° D．OD的方向是南偏东60°9、钟表盘上指示的时间是10时40分，此刻时针与分针之间的夹角为（）。

（A）60°（B）70°（C）80°（D）85°10、如图，已知∠AOC=∠BOD=900, ∠AOD=1500,则∠BOC的度数为（）A、450B、300C、500D、60011、∠α=40.4°，∠β=40°4′，则∠α与∠β的关系是（）A. ∠α=∠β；B. ∠α＞∠β；C. ∠α＜∠β；D. 以上都不对；12、如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=100°，则∠BOD的度数是（）A. 20°；B. 40°；C. 50°；D. 80°；二、填空题13、一个角的余角比这个角的补角的一半小40°，则这个角为度．14、17°14′24″＝___度．15、．计算：153°﹣26°40′=_______．16、如图所示，将图沿虚线折起来，得到一个正方体，那么“我”的对面是（填汉字）.17、图1，是一个由边长为1的小正方形木块摆放在地上而成的图形，图2，图3也是由边长为1的小正方体木块叠放在地上而成，要给露在外面的小正方体表面涂上油漆（底面不涂），按照这样的规律继续叠放下去，到第7个叠放的图形中，涂到油漆部分的面积是．18、五棱柱有__________个顶点，有__________个面，有__________条棱．19、如图，AC=CD=DE=EB,则点C是线段的中点，点D是线段的中点，如果AB=8 cm，则AD= cm,AE= cm。

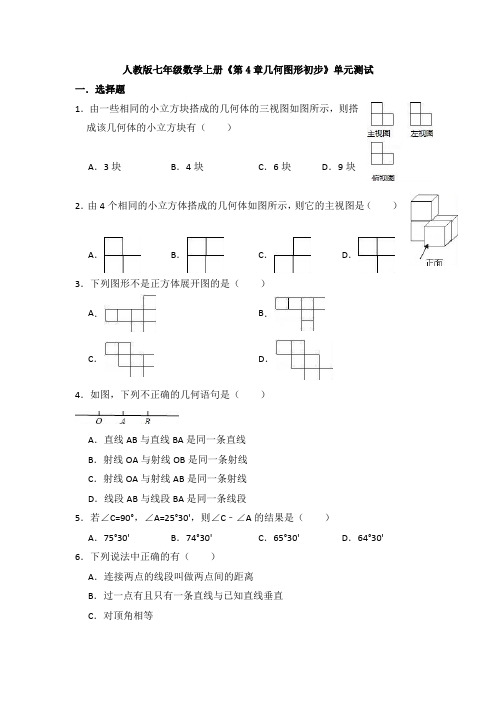
人教版七年级数学上册《第4章几何图形初步》单元测试一．选择题1．由一些相同的小立方块搭成的几何体的三视图如图所示，则搭成该几何体的小立方块有（）A．3块B．4块C．6块D．9块2．由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（）A．B．C．D．3．下列图形不是正方体展开图的是（）A．B．C．D．4．如图，下列不正确的几何语句是（）A．直线AB与直线BA是同一条直线B．射线OA与射线OB是同一条射线C．射线OA与射线AB是同一条射线D．线段AB与线段BA是同一条线段5．若∠C=90°，∠A=25°30'，则∠C﹣∠A的结果是（）A．75°30'B．74°30'C．65°30'D．64°30' 6．下列说法中正确的有（）A．连接两点的线段叫做两点间的距离B．过一点有且只有一条直线与已知直线垂直C．对顶角相等D．线段AB的延长线与射线BA是同一条射线7．如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD 内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（）A．36°B．72°C．108°D．120°8．若∠A，∠B互为补角，且∠A＜∠B，则∠A的余角是（）A．（∠A+∠B）B．∠B C．（∠B﹣∠A）D．∠A 9．如图，M是线段AB的中点，NB为MB的四分之一，MN=a，则AB表示为（）A．B．C．2a D．1.5a10．如图，将矩形ABCD沿EM折叠，使顶点B恰好落在CD边的中点N上．若AB=6，AD=9，则五边形ABMND的周长为（）A．28B．26C．25D．22二．填空题11．青青同学把一张长方形纸折了两次，如图，使点A，B都落在DG 上，折痕分别是DE，DF，则∠EDF的度数为．12．如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB=50°，则∠BOD的度数是．13．图1是一个正方体的展开图，该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格，此时这个正方体朝上一面的字是．14．如图所示的图案，可以看成是由字母“Y”绕中心每次旋转度构成的．15．如图，射线OA的方向是北偏东20°，射线OB的方向是北偏西40°，OD是OB的反向延长线．若OC是∠AOD的平分线，则∠BOC=°，射线OC的方向是．16．如图所示的三角形绕边AB所在直线旋转一周所形成的几何体是．17．一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=°．18．如图，以图中的A、B、C、D为端点的线段共有条．三．解答题19．如图，已知线段AB和CD的公共部分BD=AB=CD，线段AB、CD的中点E、F之间距离是10cm，求AB，CD的长．20．如图，直线AB、CD相交于O，∠BOC=70°，OE是∠BOC的角平分线，OF是OE的反向延长线．（1）求∠1，∠2，∠3的度数；（2）判断OF是否平分∠AOD，并说明理由．21．如图，已知OD平分∠AOB，射线OC在∠AOD内，∠BOC=2∠AOC，∠AOB=114°，求∠COD度数．22．有一个正方体，在它的各个面上分别标上数字1、2、3、4、5、6，甲、乙、丙三位同学从三个不同的角度去观察此正方体，观察结果如图所示：请画出正方体的一种表面展开图，（要求把数字标注在表面展开图中）23．将一张纸如图所示折叠后压平，点F在线段BC上，EF、GF为两条折痕，若∠1=57°，∠2=20°，求∠3的度数．24．如图，线段AC=6cm，线段BC=15cm，点M是AC的中点，在CB上取一点N，使得CN：NB=1：2，求MN的长．25．（14分）数学活动课上，小聪同学摆弄着自己刚购买的一套三角板，将两块直角三角板的直角顶点C叠放在一起，然后转动三角板，在转动过程中，请解决以下问题：（1）如图（1）：当∠DCE=30°时，∠ACB+∠DCE=，若∠DCE为任意锐角时，你还能求出∠ACB与∠DCE的数量关系吗？若能，请求出；若不能，请说明理由．（2）当转动到图（2）情况时，∠ACB与∠DCE有怎样的数量关系？请说明理由．新人教版七年级数学上册《第4章几何图形初步》单元测试参考答案与试题解析一．选择题1．B．2．A．3．B．4．C．5．D．6．C．7．B．8．C．9．A．10．A．二．填空题11．90°．12．80°．13．我．14．36．15．120，北偏东80°．16．圆锥．17．40．18．6．三．解答题19．解：设BD=xcm，则AB=3xcm，CD=4xcm，AC=6xcm．∵点E、点F分别为AB、CD的中点，∴AE=AB=1.5xcm，CF=CD=2xcm．∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm．∵EF=10cm，∴2.5x=10，解得：x=4．∴AB=12cm，CD=16cm．20．解：（1）∵∠BOC+∠2=180°，∠BOC=70°，∴∠2=180°﹣70°=110°；∵OE是∠BOC的角平分线，∴∠1=35°．∵∠1+∠2+∠3=180°，∴∠3=180°﹣∠1﹣∠2=180°﹣35°﹣110°=35°．（2）∵∠2+∠3+∠AOF=180°，∴∠AOF=180°﹣∠2﹣∠3=180°﹣110°﹣35°=35°．∴∠AOF=∠3=35°，∴OF平分∠AOD．21．解：∵OD平分∠AOB，∴∠AOD=∠AOB=×114°=57°，∵∠BOC=2∠AOC，∠AOB=114°，∴∠AOC=∠AOB=×114°=38°，∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°．22．解：从3个小立方体上的数可知，与写有数字1的面相邻的面上数字是2，3，4，6，所以数字1面对数字5面，同理，立方体面上数字3对6．故立方体面上数字2对4．作图为：23．解：如图由折叠可知，∠EFB′=∠1=57°，∠2=20°，∠3=∠GFC′，∵∠EFB′+∠1+∠2+∠3+∠GFC′=180°，∴∠3==23°．24．解：∵M是AC的中点，∴MC=AM=AC=×6=3cm，又∵CN：NB=1：2∴CN=BC=×15=5cm，∴MN=MC+NC=3cm+5cm=8cm．25．解：（1）∠ACB+∠DCE=180°；若∠DCE为任意锐角时，∠ACB+∠DCE=180°，理由如下：∵∠ACE+∠DCE=90°，∠BCD+∠DCE=90°，∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°；（2）∠ACB+∠DCE=180°．理由如下：∵∠ACD=90°=∠ECB，∠ACD+∠ECB+∠ACB+∠DCE=360°，∴∠ECD+∠ACB=360°﹣（∠ACD+∠ECB）=360°﹣180°=180°人教版七年级数学上册《第4章几何图形初步》单元测试一．选择题1．由一些相同的小立方块搭成的几何体的三视图如图所示，则搭成该几何体的小立方块有（）A．3块B．4块C．6块D．9块2．由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（）A．B．C．D．3．下列图形不是正方体展开图的是（）A．B．C．D．4．如图，下列不正确的几何语句是（）A．直线AB与直线BA是同一条直线B．射线OA与射线OB是同一条射线C．射线OA与射线AB是同一条射线D．线段AB与线段BA是同一条线段5．若∠C=90°，∠A=25°30'，则∠C﹣∠A的结果是（）A．75°30'B．74°30'C．65°30'D．64°30'6．下列说法中正确的有（）A．连接两点的线段叫做两点间的距离B．过一点有且只有一条直线与已知直线垂直C．对顶角相等D．线段AB的延长线与射线BA是同一条射线7．如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD 内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（）A．36°B．72°C．108°D．120°8．若∠A，∠B互为补角，且∠A＜∠B，则∠A的余角是（）A．（∠A+∠B）B．∠B C．（∠B﹣∠A）D．∠A 9．如图，M是线段AB的中点，NB为MB的四分之一，MN=a，则AB表示为（）A．B．C．2a D．1.5a10．如图，将矩形ABCD沿EM折叠，使顶点B恰好落在CD边的中点N上．若AB=6，AD=9，则五边形ABMND的周长为（）A．28B．26C．25D．22二．填空题11．青青同学把一张长方形纸折了两次，如图，使点A，B都落在DG 上，折痕分别是DE，DF，则∠EDF的度数为．12．如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB=50°，则∠BOD的度数是．13．图1是一个正方体的展开图，该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格，此时这个正方体朝上一面的字是．14．如图所示的图案，可以看成是由字母“Y”绕中心每次旋转度构成的．15．如图，射线OA的方向是北偏东20°，射线OB的方向是北偏西40°，OD是OB的反向延长线．若OC是∠AOD的平分线，则∠BOC=°，射线OC的方向是．16．如图所示的三角形绕边AB所在直线旋转一周所形成的几何体是．17．一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=°．18．如图，以图中的A、B、C、D为端点的线段共有条．三．解答题19．如图，已知线段AB和CD的公共部分BD=AB=CD，线段AB、CD的中点E、F之间距离是10cm，求AB，CD的长．20．如图，直线AB、CD相交于O，∠BOC=70°，OE是∠BOC的角平分线，OF是OE的反向延长线．（1）求∠1，∠2，∠3的度数；（2）判断OF是否平分∠AOD，并说明理由．21．如图，已知OD平分∠AOB，射线OC在∠AOD内，∠BOC=2∠AOC，∠AOB=114°，求∠COD度数．22．有一个正方体，在它的各个面上分别标上数字1、2、3、4、5、6，甲、乙、丙三位同学从三个不同的角度去观察此正方体，观察结果如图所示：请画出正方体的一种表面展开图，（要求把数字标注在表面展开图中）23．将一张纸如图所示折叠后压平，点F在线段BC上，EF、GF为两条折痕，若∠1=57°，∠2=20°，求∠3的度数．24．如图，线段AC=6cm，线段BC=15cm，点M是AC的中点，在CB上取一点N，使得CN：NB=1：2，求MN的长．25．（14分）数学活动课上，小聪同学摆弄着自己刚购买的一套三角板，将两块直角三角板的直角顶点C叠放在一起，然后转动三角板，在转动过程中，请解决以下问题：（1）如图（1）：当∠DCE=30°时，∠ACB+∠DCE=，若∠DCE为任意锐角时，你还能求出∠ACB与∠DCE的数量关系吗？若能，请求出；若不能，请说明理由．（2）当转动到图（2）情况时，∠ACB与∠DCE有怎样的数量关系？请说明理由．新人教版七年级数学上册《第4章几何图形初步》单元测试参考答案与试题解析一．选择题1．B．2．A．3．B．4．C．5．D．6．C．7．B．8．C．9．A．10．A．二．填空题11．90°．12．80°．13．我．14．36．15．120，北偏东80°．16．圆锥．17．40．18．6．三．解答题19．解：设BD=xcm，则AB=3xcm，CD=4xcm，AC=6xcm．∵点E、点F分别为AB、CD的中点，∴AE=AB=1.5xcm，CF=CD=2xcm．∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm．∵EF=10cm，∴2.5x=10，解得：x=4．∴AB=12cm，CD=16cm．20．解：（1）∵∠BOC+∠2=180°，∠BOC=70°，∴∠2=180°﹣70°=110°；∵OE是∠BOC的角平分线，∴∠1=35°．∵∠1+∠2+∠3=180°，∴∠3=180°﹣∠1﹣∠2=180°﹣35°﹣110°=35°．（2）∵∠2+∠3+∠AOF=180°，∴∠AOF=180°﹣∠2﹣∠3=180°﹣110°﹣35°=35°．∴∠AOF=∠3=35°，∴OF平分∠AOD．21．解：∵OD平分∠AOB，∴∠AOD=∠AOB=×114°=57°，∵∠BOC=2∠AOC，∠AOB=114°，∴∠AOC=∠AOB=×114°=38°，∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°．22．解：从3个小立方体上的数可知，与写有数字1的面相邻的面上数字是2，3，4，6，所以数字1面对数字5面，同理，立方体面上数字3对6．故立方体面上数字2对4．作图为：23．解：如图由折叠可知，∠EFB′=∠1=57°，∠2=20°，∠3=∠GFC′，∵∠EFB′+∠1+∠2+∠3+∠GFC′=180°，∴∠3==23°．24．解：∵M是AC的中点，∴MC=AM=AC=×6=3cm，又∵CN：NB=1：2∴CN=BC=×15=5cm，∴MN=MC+NC=3cm+5cm=8cm．25．解：（1）∠ACB+∠DCE=180°；若∠DCE为任意锐角时，∠ACB+∠DCE=180°，理由如下：∵∠ACE+∠DCE=90°，∠BCD+∠DCE=90°，∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°；（2）∠ACB+∠DCE=180°．理由如下：∵∠ACD=90°=∠ECB，∠ACD+∠ECB+∠ACB+∠DCE=360°，∴∠ECD+∠ACB=360°﹣（∠ACD+∠ECB）=360°﹣180°=180°人教版七年级数学上册第四章几何图形初步单元测试B卷一、填空题1．已知线段AB＝8 cm，在直线AB上画线段BC使BC＝3 cm，则线段AC＝．2．如图是某个几何体的表面展开图，那么这个几何体是．3．如图，点A，B，C在直线l上，则图中共有条线段，有条射线．4．如图，点O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，则这三个角的度数分别是．5．如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOD＝120°，则∠DOE＝，∠COE＝．6．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为．二、选择题7.如图的几何体，从左边看到的图是 （ ）8.下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（） A ．用两个钉子就可以把木条固定在墙上 B ．利用圆规可以比较两条线段的大小关系 C ．把弯曲的公路改直，就能缩短路程D ．植树时，只要定出两棵树的位置，就能确定同一行树所在的直线 9. 如图，直线AB ，CD 交于点O ，射线OM 平分∠AOC ，若 ∠AOC ＝76°，则∠BOM 等于（） A ．38°B ．104°C ．142°D ．144°10.将两块直角三角板的直角顶点重合，如图所示，若， 则∠BOC 的度数是（）．A. 45° B .52° C. 60° D. 50° 11.下列说法中错误的有().128AOD∠第3题第4题(1)线段有两个端点，直线有一个端点; (2)角的大小与我们画出的角的两边的长短无关; (3)线段上有无数个点; (4)同角或等角的补角相等; (5)两个锐角的和一定大于直角.A ．1个B ．2个C ．3个D ．4个12.下列四个图中，能用上∠1、∠AOB 、∠O 三种方法表示同一个的是( ).13.对于直线AB ，线段CD ，射线EF ，在下列各图中能相交的是( ).14.在海上，灯塔位于一艘船的北偏东40°方向，那么这艘船位于这个灯塔的( ). A ：南偏西50°方向 B ：南偏西40°方向 C ：北偏东50°方向 D ：北偏东40°方向15.如图，四个图形是由立体图形展开得到的，相应的立体图形顺次是（） A. 正方体、圆柱、三棱柱、圆锥B. 正方体、圆锥、三棱柱、圆柱C. 正方体、圆柱、三棱锥、圆锥D. 正方体、圆柱、四棱柱、圆锥16.点E 在线段CD 上，下面四个等式①CE ＝DE ；②DE ＝21CD ；③CD ＝2CE ； ④CD ＝21DE.其中能表示E 是线段CD 中点的有（） A. 1个 B. 2个 C. 3个 D. 4个 三、解答题17．一个角的补角比它的余角的3倍小20°，求这个角的度数．18．(1)如图1，已知点D是线段AC的中点，点B在线段DC上，且AB＝4BC，若BD＝6 cm，求AB的长；(2)如图2，∠AOB＝∠COD＝90°，OC平分∠AOB，∠BOD＝3∠DOE，试求∠COE的度数.19．如图，已知线段AB上有两点C，D，且AC∶CD∶DB＝2∶3∶4，E，F分别为AC，DB的中点，EF＝2.4 cm，求线段AB的长．20．(12分)如图，P是线段AB上任一点，AB＝12 cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2 cm/s，D点的运动速度为3 cm/s，运动的时间为t s.(1)若AP＝8 cm.①运动1 s 后，求CD 的长；②当D 在线段PB 运动上时，试说明AC ＝2CD ； (2)如果t ＝2 s 时，CD ＝1 cm ，试探索AP 的值．参考答案一、填空题1．已知线段AB ＝8 cm ，在直线AB 上画线段BC 使BC ＝3 cm ，则线段AC ＝ 5cm 或11cm ． 2．如图是某个几何体的表面展开图，那么这个几何体是圆锥．3．如图，点A ，B ，C 在直线l 上，则图中共有3条线段，有 6条射线．4．如图，点O 是直线AD 上的点，∠AOB ，∠BOC ，∠COD 三个角从小到大依次相差25°，则这三个角的度数分别是 35°，60°，85°．5．如图，直线AB 、CD 相交于点O ，OE 平分∠BOD ，∠AOD ＝120°，则∠DOE ＝30° ，∠COE ＝ 150°．6．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n 条直线最多可将平面分成56个部分，则n 的值为10．二、选择题7.如图的几何体，从左边看到的图是 （ B ）。

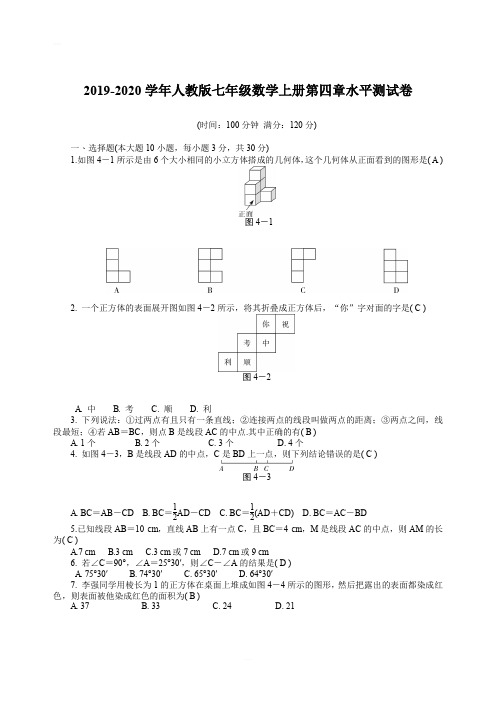
2019-2020学年人教版七年级数学上册第四章水平测试卷(时间：100分钟 满分：120分)一、选择题(本大题10小题，每小题3分，共30分)1.如图4－1所示是由6个大小相同的小立方体搭成的几何体，这个几何体从正面看到的图形是( A )图4－12. 一个正方体的表面展开图如图4－2所示，将其折叠成正方体后，“你”字对面的字是( C )图4－2A . 中B . 考C . 顺D . 利3. 下列说法：①过两点有且只有一条直线；②连接两点的线段叫做两点的距离；③两点之间，线段最短；④若AB ＝BC ，则点B 是线段AC 的中点.其中正确的有( B )A . 1个B . 2个C . 3个D . 4个4. 如图4－3，B 是线段AD 的中点，C 是BD 上一点，则下列结论错误的是( C )图4－3A . BC ＝AB －CD B . BC ＝12AD －CD C . BC ＝12(AD ＋CD) D . BC ＝AC －BD5.已知线段AB ＝10 cm ，直线AB 上有一点C ，且BC ＝4 cm ，M 是线段AC 的中点，则AM 的长为( C )A .7 cmB .3 cmC .3 cm 或7 cmD .7 cm 或9 cm 6. 若∠C ＝90°，∠A ＝25°30′，则∠C －∠A 的结果是( D ) A . 75°30′ B . 74°30′ C . 65°30′ D . 64°30′7. 李强同学用棱长为1的正方体在桌面上堆成如图4－4所示的图形，然后把露出的表面都染成红色，则表面被他染成红色的面积为( B )A . 37B . 33C . 24 D. 21图4－4图4－58. 如图4－5，在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为( C )A. 69°B. 111°C. 141°D. 159°9. 如果∠1与∠2互补，∠2与∠3互余，那么∠1与∠3的关系是( C )A. ∠1＝∠3B. ∠1＝180°－∠3C. ∠1＝90°＋∠3D. 以上都不对10.一副三角板按图4－6所示方式摆放，且∠1的度数比∠2的度数小20°，则∠1的度数为( A )图4－6A.35°B.30°C.25°D.20°二、填空题(本大题6小题，每小题4分，共24分)11.若∠1＝30°28′，则∠1的余角等于59°32′ .12. 如图4－7，从甲村到乙村共有三条路，小明选择第②条路最近，所用的数学知识为两点之间，线段最短.图4－7图4－813.如图4－8所示是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的图形，则搭成这个几何体的小正方体的个数是7 个.14. 如果∠α与∠β互补，且∠α：∠β＝5：4，那么∠α＝100°，∠β＝80° .15.延长线段AB到C，使BC＝4，若AB＝8，则线段AC的长为12 .16. 32.48°＝32 度28 分48 秒.教与学广东学导练数学七年级上册配人教版第四章水平测试卷第2页(共4页)三、解答题(一)(本大题3小题，每小题6分，共18分)17. 计算：(1)48°39′＋67°31′；(2)78°－47°34′56″；(3)22°16′×5.解：原式＝116°10′.解：原式＝30°25′4″.解：原式＝111°20′.18. 如图4－9，已知A，B，C，D四点，根据下列语句画图.(1)画直线AB；(2)连接AC，BD，相交于点O；(3)画射线AD，BC，交于点P.图4－9答图4－1解：(1)如答图4－1，直线AB即为所求.(2)如答图4－1，线段AC，BD，点O即为所求.(3)如答图4－1，射线AD，BC，点P即为所求.19. 一个角的补角和这个角的余角的2倍互为补角，求这个角的度数.解：设这个角为x°，则这个角的余角为(90－x)°，补角为(180－x)°. 则有(180－x)＋2(90－x)＝180.解得x＝60.答：这个角的度数为60°.四、解答题(二)(本大题3小题，每小题7分，共21分)20. 如图4－10，OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC＝130°，求∠DOE的度数.图4－10解：因为OD 是∠AOB 的平分线，OE 是∠BOC 的平分线，且∠AOC ＝130°， 所以∠AOD ＝∠BOD ，∠BOE ＝∠COE.所以∠DOE ＝12∠AOC ＝65°.21.如图4－11所示是由5个相同的小正方体搭成的几何体，已知小正方体的棱长为1.图4－11(1)在网格中画出从三个方向看这个几何体得到的图形； (2)求出这个几何体的表面积(含底面积). 解：(1)如答图4－2.答图4－2(2)这个几何体的表面积为2×(4＋4＋3)＝22.22.如图4－12，已知线段A B .(1)作图：延长线段AB 到点C ，使AC ＝3AB ；(2)在(1)所画图中，若AB ＝1 cm ，D 为AB 的中点，E 为AC 的中点，求DE 的长.图4－12解：(1)如答图4－3.答图4－3(2)因为AB ＝1 cm ，D 为AB 的中点，所以AD ＝0.5 cm . 因为AC ＝3AB ，所以AC ＝3 cm .因为E 为AC 的中点，所以AE ＝1.5 cm . 所以DE ＝AE －AD ＝1 cm.五、解答题(三)(本大题3小题，每小题9分，共27分)23. 一个几何体由若干个相同的小正方体组成，如图4－13是从上面看得到的图形，其中每个小正方形中的数字代表该位置小正方体的个数，请画出该几何体从正面和从左面看得到的图形.图4－13解：从正面看和从左面看得到的图形如答图4－4.答图4－424.如图4－14，已知线段AB.(1)请用尺规按下列要求作图：①延长线段AB到C，使BC＝AB，②延长线段BA到D，使AD＝AC(不写画法，但要保留画图痕迹)；(2)请直接回答线段BD与线段AC长度之间的大小关系；(3)如果AB＝2 cm，请求出线段BD和CD的长度.图4－14解：(1)如答图4－5，BC，AD即为所求.答图4－5(2)由答图4－5可得，BD＞AC.(3)因为AB＝2 cm，所以AC＝2AB＝4 cm.所以AD＝4 cm.所以BD＝4＋2＝6(cm).所以CD＝2AD＝8 cm.25. 如图4－15，已知∠AOM与∠MOB互为余角，且∠BOC＝30°，OM平分∠AOC，ON平分∠BOC.(1)求∠MON的度数；(2)如果已知中∠AOB＝80°，其他条件不变，求∠MON的度数；(3)如果已知中∠BOC＝60°，其他条件不变，求∠MON的度数；(4)从(1)(2)(3)中你能发现什么规律？图4－15 解：(1)因为OM 平分∠AOC ，所以∠MOC ＝12∠AOC.又ON 平分∠BOC ，所以∠NOC ＝12∠BOC.所以∠MON ＝∠MOC －∠NOC ＝12∠AOC －12∠BOC ＝12∠AOB.而∠AOB ＝90°，所以∠MON ＝45°.(2)当∠AOB ＝80°，其他条件不变时，∠MON ＝12×80°＝40°.(3)当∠BOC ＝60°，其他条件不变时，∠MON ＝45°. (4)分析(1)(2)(3)的结果和(1)的解答过程可知，∠MON 的大小总等于∠AOB 的一半，而与锐角∠BOC 的大小无关。

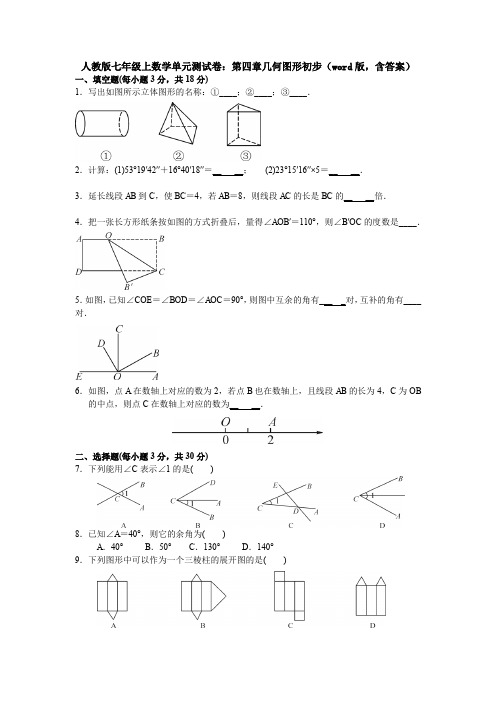
人教版七年级上数学单元测试卷：第四章几何图形初步（word版，含答案）一、填空题(每小题3分，共18分)1．写出如图所示立体图形的名称：①____；②____；③____．2．计算：(1)53°19′42″＋16°40′18″＝__ __；(2)23°15′16″×5＝__ __．3．延长线段AB到C，使BC＝4，若AB＝8，则线段AC的长是BC的__ __倍．4．把一张长方形纸条按如图的方式折叠后，量得∠AOB′＝110°，则∠B′OC的度数是____．5．如图，已知∠COE＝∠BOD＝∠AOC＝90°，则图中互余的角有___ _对，互补的角有____对．6．如图，点A在数轴上对应的数为2，若点B也在数轴上，且线段AB的长为4，C为OB 的中点，则点C在数轴上对应的数为__ __．二、选择题(每小题3分，共30分)7．下列能用∠C表示∠1的是( )8．已知∠A＝40°，则它的余角为( )A．40°B．50°C．130°D．140°9．下列图形中可以作为一个三棱柱的展开图的是( )10．下面四个几何体中，从左面看到的图形是四边形的几何体共有( )A ．1个B ．2个C ．3个D ．4个11．已知M 是线段AB 的中点，那么：①AB ＝2AM ；②BM ＝12AB ；③AM ＝BM ；④AM ＋BM ＝AB ，上面四个式子中，正确的个数有( ) A ．1个 B ．2个 C ．3个 D ．4个12．如图，已知∠1＝∠2，∠3＝∠4，则下列结论：①AD 平分∠BAF ；②AF 平分∠DAC ；③AE 平分∠DAF ；④AE 平分∠BAC ，其中正确的个数是( ) A ．1 B ．2 C ．3 D ．413．平面上五个点最多可以确定直线的条数为( )A ．5条B ．8条C ．10条D ．12条 14．如图，直线l 1，l 2，l 3把平面分成( )部分．A ．4B ．5C ．6D ．715．如图，在时刻8：30，时钟上的时针和分针之间的夹角为( ) A ．85° B ．75° C ．70° D ．60°16．如果AB ＝10 cm ，BC ＝8 cm ，则A ，C 两点间的距离为( ) A ．2 cm B ．18 cm C ．2 cm 或18 cm D ．不能确定 三、解答题(共52分)17．(8分)如图是由七块相同的小正方体搭成的立体图形，请画出这个图形分别从正面看、从左面看和从上面看到的平面图形．18．(8分)如图，两辆汽车从A 点同时出发，一辆沿西北方向以40千米/时的速度行驶；另一辆沿南偏西60°的方向以60千米/时的速度行驶，34小时后分别到达B ，C 两点，如果图中1 cm 代表10 km ，那么试在图中画出B ，C 两点，并通过测量，说出此时两辆车的距离．19．(8分)如图，已知A ，B ，C 三点在同一直线上，AB ＝24 cm ，BC ＝38AB ，E 是AC 的中点，D 是AB 的中点，求DE 的长．20．(8分)如图，点A ，O ，B 在同一条直线上，∠COB 与∠BOD 互余，OE ，OF 分别是∠AOC，∠AOD的平分线，求∠EOF的度数．21．(8分)如图，A，O，E在一条直线上，OB平分∠AOC，∠AOB＋∠DOE＝90°，问∠COD 与∠DOE之间有什么关系？并说明理由．22．(12人教版七年级上册第四章几何图形初步单元测试卷一、选择题(每小题3分,共30分)1.(2017广西河池中考)如图4-5-1,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )图4-5-1A.60°B.90°C.120°D.150°2.下面说法:①若线段AC=BC,则C是线段AB的中点;②两点之间,直线最短;③延长直线AB;④若一个角既有余角又有补角,则它的补角一定比它的余角大.其中正确的有( )3.(2017四川南充中考)图4-5-2是由7个小正方体组合而成的几何体,从正面看,所看到的图形是( )图4-5-24.如图4-5-3所示,小于平角的角有( )图4-5-3A.9个B.8个C.7个D.6个5.如图4-5-4,C、D是线段AB上两点,若BC=3 cm,BD=5 cm,且D是AC的中点,则AC的长为( )图4-5-4A.2 cmB.4 cmC.8 cmD.13 cm6.小明由点A出发向正东方向走10 m到达点B,再由点B向东南方向走10 m到达点C,则下列结论正确的是( )A.∠ABC=22.5°B.∠ABC=45°C.∠ABC=67.5°D.∠ABC=135°7.如图4-5-5所示,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式正确的是( )图4-5-5A.∠COD=∠AOBB.∠AOD=∠AOBC.∠BOD=∠AOBD.∠BOC=∠AOD8.(2017湖南张家界中考)如图4-5-6是一个正方体的表面展开图,则正方体中与“美”字所在面相对的面上标的字是( )图4-5-6A.丽B.张C.家D.界9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点分别为D、E,则线段DE的长为( )A.5B.3C.1D.5或310.(2017山西忻州一中期末)如图4-5-7,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )图4-5-7①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=∠BOD.A.1个B.2个C.3个D.4个二、填空题(每小题3分,共30分)11.(2017浙江诸暨中学期末)∠AOB的大小可由量角器测得(如图4-5-8所示),则∠AOB 的补角的大小为.图4-5-812.如图4-5-9所示,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC长的倍.图4-5-913.如果一个角的补角是150°,那么这个角的余角为°.14.如图4-5-10,已知M、N分别是AC、CB的中点,MN=6 cm,则AB= cm.图4-5-1015.如图4-5-11所示,O是直线AB上一点,OC是∠AOB的平分线.图4-5-11(1)图中互余的角是;(2)图中互补的角是.16.如图4-5-12,∠AOB=90°,∠BOC=30°,OD平分∠AOC,则∠BOD=.图4-5-1217.(2017贵州安顺西秀旧州中学期末)如图4-5-13所示,已知∠AOB=70°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF的度数是.图4-5-1318.点A、B、C是数轴上的三个点,且BC=2AB.已知点A表示的数是-1,点B表示的数是3,点C表示的数是.19.如图4-5-14,OM、ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.图4-5-14(1)∠MON=;(2)当OC在∠AOB内绕点O转动时,∠MON的值改变.(填“会”或“不会”)20.如图4-5-15,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是.图4-5-15三、解答题(共40分)21.(8分)计算:(1)48°39'40″+67°41'35″;(2)49°28'52″÷4.22.(6分)如果一个角的余角是它的补角的,求这个角的度数.23.(6分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.(1)准确地画出图形,并标出相应的字母;(2)哪个点是线段DC的中点?线段AB的长是线段DC长的几分之几?(3)求出线段BD的长度.24.(6分)如图4-5-16所示,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠BOC的度数.图4-5-1625.(6分)图4-5-17是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.(1)把-10,8,10,-3,-8,3分别填入图中的六个小正方形中;(2)若某两个相对面上的数字分别为-和-5,求x的值.图4-5-1726.(8分)如图4-5-18所示,请按照要求解答问题.(1)数轴上的点C在2、3的正中间位置,则点C表示的数是,线段AB的中点D 表示的数是;(2)线段AB的中点D与线段BC的中点E的距离为;(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,并判断BC是否平分∠MBN.简要说明理由.图4-5-18第四章几何图形初步答案解析一、选择题(每小题3分,共30分)1.(2017广西河池中考)如图4-5-1,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )图4-5-1A.60°B.90°C.120°D.150°答案 C ∵∠BOC=60°,∠BOC+∠AOC=180°,∴∠AOC=120°.2.下面说法:①若线段AC=BC,则C是线段AB的中点;②两点之间,直线最短;③延长直线AB;④若一个角既有余角又有补角,则它的补角一定比它的余角大.其中正确的有( )A.0个B.1个C.2个D.3个答案 B ①如图,C不是线段AB的中点,故①不正确;②两点之间,线段最短,故②不正确;③直线向两边无限延伸,不能延长,故③不正确;④正确,故选B.3.(2017四川南充中考)图4-5-2是由7个小正方体组合而成的几何体,从正面看,所看到的图形是( )图4-5-2答案 A 从正面看所得的图形就是从前向后看立体图形所得到的平面图形.可看到四个正方形,其中左边从上到下共有3个正方形,右边只有1个正方形.故选A.4.如图4-5-3所示,小于平角的角有( )图4-5-3A.9个B.8个C.7个D.6个答案 C 符合条件的角中以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,共有1+2+1+1+2=7(个)角,故选C.5.如图4-5-4,C、D是线段AB上两点,若BC=3 cm,BD=5 cm,且D是AC的中点,则AC的长为( )图4-5-4A.2 cmB.4 cmC.8 cmD.13 cm答案 B ∵BC=3 cm,BD=5 cm,∴CD=BD-BC=2 cm,∵D是AC的中点,∴AC=2CD=4 cm,故选B.6.小明由点A出发向正东方向走10 m到达点B,再由点B向东南方向走10 m到达点C,则下列结论正确的是( )A.∠ABC=22.5°B.∠ABC=45°C.∠ABC=67.5°D.∠ABC=135°答案 D 由题意作图如下:由图可得∠ABC=90°+45°=135°.7.如图4-5-5所示,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式正确的是( )图4-5-5A.∠COD=∠AOBB.∠AOD=∠AOBC.∠BOD=∠AOBD.∠BOC=∠AOD答案 D 设∠COD=x,因为OD平分∠BOC,所以∠BOD=∠COD=x,∠BOC=2x.又OC平分∠AOB,所以∠AOC=∠BOC=2x,则∠AOB=4x,所以∠COD=∠AOB,∠AOD=∠AOB,∠BOD=∠AOB,∠BOC=∠AOD,故选D.8.(2017湖南张家界中考)如图4-5-6是一个正方体的表面展开图,则正方体中与“美”字所在面相对的面上标的字是( )图4-5-6A.丽B.张C.家D.界答案 C 同一行或列中,中间间隔一个小正方形的两个小正方形在正方体中就是一对相对面,所以“丽”与“张”相对;相对面不共顶点,所以“的”与“美”“家”不相对,从而“的”与“界”相对;因此剩下的两个字“美”与“家”是相对的.9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点分别为D、E,则线段DE的长为( )A.5B.3C.1D.5或3答案 D 如图1,DE=3;如图2,DE=5.图1 图210.(2017山西忻州一中期末)如图4-5-7,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )图4-5-7①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=∠BOD.A.1个B.2个C.3个D.4个答案 C 因为∠AOD=110°,∠BOC=70°,所以∠COD+∠AOB=40°,又因为∠AOB=∠COD,所以∠AOB=∠COD=20°,所以∠AOC=∠BOD=90°,故①②正确;∠AOD-∠AOC=∠COD=∠AOB,故③正确;∠AOB=∠BOD,故④不正确.所以正确的有3个.二、填空题(每小题3分,共30分)11.(2017浙江诸暨中学期末)∠AOB的大小可由量角器测得(如图4-5-8所示),则∠AOB 的补角的大小为.图4-5-8答案120°解析由题图知∠AOB=60°,所以∠AOB的补角的大小为180°-60°=120°.12.如图4-5-9所示,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC长的倍.图4-5-9答案 3解析由题图可知AC=AB+BC=8+4=12,所以AC=3BC.13.如果一个角的补角是150°,那么这个角的余角为°.答案60解析因为180°-150°=30°,所以这个角的大小为30°,所以这个角的余角为90°-30°=60°.14.如图4-5-10,已知M、N分别是AC、CB的中点,MN=6 cm,则AB= cm.图4-5-10答案12解析因为M、N分别是AC、CB的中点,所以CM=AC,CN=CB,则AB=AC+BC=2CM+2CN=2(CM+CN)=2MN=2×6=12(cm).15.如图4-5-11所示,O是直线AB上一点,OC是∠AOB的平分线.图4-5-11(1)图中互余的角是;(2)图中互补的角是.答案(1)∠AOD与∠DOC(2)∠AOD与∠BOD,∠AOC与∠BOC解析(1)因为O是直线AB上一点,OC是∠AOB的平分线,所以∠AOC=∠BOC=∠AOB=90°,所以∠AOD+∠DOC=90°,即∠AOD与∠DOC互余.(2)∠AOD+∠BOD=180°,∠AOC+∠BOC=180°,即∠AOD与∠BOD互补,∠AOC与∠BOC互补.16.如图4-5-12,∠AOB=90°,∠BOC=30°,OD平分∠AOC,则∠BOD=.图4-5-12答案30°解析因为∠AOB=90°,∠BOC=30°,所以∠AOC=90°+30°=120°.又因为OD平分∠AOC,所以∠COD=∠AOC=60°,所以∠BOD=∠COD-∠COB=60°-30°=30°.17.(2017贵州安顺西秀旧州中学期末)如图4-5-13所示,已知∠AOB=70°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF的度数是.图4-5-13答案45°解析因为OE平分∠AOB,OF平分∠BOC,所以∠EOB=×70°=35°,∠BOF=×20°=10°,故∠EOF=∠EOB+∠BOF=35°+10°=45°.18.点A、B、C是数轴上的三个点,且BC=2AB.已知点A表示的数是-1,点B表示的数是3,点C表示的数是.答案-5或11解析AB=3-(-1)=4,因为点A、B、C是数轴上的三个点,且BC=2AB,所以BC的长为8,所以点C表示的数为3+8=11或3-8=-5.19.如图4-5-14,OM、ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.图4-5-14(1)∠MON=;(2)当OC在∠AOB内绕点O转动时,∠MON的值改变.(填“会”或“不会”)答案(1)42°(2)不会解析(1)∠MON=∠MOC+∠NOC=∠BOC+∠AOC=(∠BOC+∠AOC)=×∠AOB=×84°=42°.(2)由(1)可知,∠MON=∠AOB,∴∠MON的值不会随着OC在∠AOB内绕点O转动而改变.20.如图4-5-15,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是.图4-5-15答案90°解析由折叠可知,∠CFG=∠EFG=∠CFE,因为FH平分∠BFE,所以∠EFH=∠BFH=∠EFB.因为∠CFG+∠EFG+∠EFH+∠BFH=180°,所以∠GFH=∠EFG+∠EFH=90°.三、解答题(共40分)21.(8分)计算:(1)48°39'40″+67°41'35″;(2)49°28'52″÷4.解析(1)48°39'40″+67°41'35″=115°80'75″=116°21'15″.(2)49°28'52″÷4=12°+88'52″÷4=12°22'+52″÷4=12°22'13″.22.(6分)如果一个角的余角是它的补角的,求这个角的度数.解析设这个角的度数为x°,则它的余角为(90-x)°,它的补角为(180-x)°,根据题意得90-x=×(180-x),解得x=30.答:这个角的度数是30°.23.(6分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.(1)准确地画出图形,并标出相应的字母;(2)哪个点是线段DC的中点?线段AB的长是线段DC长的几分之几?(3)求出线段BD的长度.解析(1)如图.(2)点A是线段DC的中点,AB=CD.(3)BC=AB=×2=1(cm),因而AC=AB+BC=2+1=3(cm).所以AD=AC=3 cm,故BD=DA+AB=3+2=5(cm).24.(6分)如图4-5-16所示,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠BOC的度数.图4-5-16解析因为OE平分∠AOB,∠AOB=90°,所以∠BOE=45°.又∠EOF=60°,所以∠BOF=∠EOF-∠BOE=60°-45°=15°.又因为OF平分∠BOC,所以∠BOC=2∠BOF=30°,所以∠AOC=∠AOB+∠BOC=90°+30°=120°.25.(6分)图4-5-17是一个正方体盒子的表面展开图,该正方体六个面上人教版七年级上册第三章一元一次方程单元测试卷一．选择题（共12小题，共36分）1．下列说法：①直线AB和直线BA是同一条直线；②平角是一条直线；③两点之间，线段最短；④如果AB=BC，则点B是线段AC的中点．其中正确的有（）A．1个B．2个C．3个D．4个2．如过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图所示的几何体，其正确展开图为（）A．B．C．D．3．如图，C，D是线段AB上两点，若CB=4cm，DB=7cm，且D是AC的中点，则AB的长等于（）A．6cm B．7cm C．10cm D．11cm4．如图是某几何体的表面展开图，则该几何体是（）A．三棱锥B．三棱柱C．四棱锥D．四棱柱5．时钟的时间是3点30分，时钟面上的时针与分针的夹角是（）A．90°B．100°C．75°D．105°6．如果∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系是（）A．∠1=∠3B．∠1=180°﹣∠3C．∠1=90°+∠3D．以上都不对7．下列说法正确的是（）A．射线比直线短B．小于平角的角可分为锐角和钝角两类C．两条射线组成的图形叫做角D．一个角的补角不一定比这个角大8．下列说法错误的是（）A．长方体、正方体都是棱柱B．圆锥和圆柱的底面都是圆C．三棱柱的底面是三角形D．六棱柱有6条棱、6个侧面、侧面为长方形9．点C在线段AB上，下列条件中不能确定点C是线段AB中点的是（）A．AC=BC B．AC+BC=AB C．AB=2AC D．BC=AB 10．如图是一个正方体包装盒的表面展开图，若在其中的三个正方形A、B、C 内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在A、B、C的三个数依次是（）A．0，﹣3，4B．0，4，﹣3C．4，0，﹣3D．﹣3，0，4 11．如图，∠AOB是直角，OA平分∠COD，OE平分∠BOD，若∠BOE=23°，则∠BOC的度数是（）A．113°B．134°C．136°D．144°12．把14个棱长为1的正方体，在地面上堆叠成如图所示的立方体，然后将露出的表面部分染成红色，那么红色部分的面积为（）A．21B．24C．33D．37二．填空题（共6小题，共18分）13．一个漂亮的礼物盒是一个有11个面的棱柱，那么它有个顶点．14．把一副三角板按照如图所示的位置拼在一起，不重叠也没有缝隙，则∠ABC 的度数为．15．已知∠AOB=80°，∠BOC=40°，射线OM是∠AOB平分线，射线ON是∠BOC 平分线，则∠MON=．16．如图，已知C为线段AB的中点，D在线段CB上．若DA=6，DB=4，则CD=．17．如图是正方体的一个表面展开图，在这个正方体中，与“晋”字所在面相对的面上的汉字是．18．如图，C、D、E为线段AB上三点，且AC=CD，E为BD的中点，DE=AB=2cm，则CE的长为cm．三．解答题（共6小题，共46分）19．如图，OD是∠AOB的平分线，OE是∠BOC的平分线．（1）若∠BOC=50°，∠BOA=80°，求∠DOE的度数；（2）若∠AOC=150°，求∠DOE的度数；（3）你发现∠DOE与∠AOC有什么等量关系？给出结论并说明．20．某公园有海盗船、摩天轮、碰碰车三个娱乐项目，现要在公园内建一个售票中心，使三个娱乐项目所处位置到售票中心的距离相等，请在图中确定售票中心的位置．21．某宾馆大堂有6 根圆柱形大柱，高10 米，大柱周长25.12 分米，要全部涂上油漆，如果按每平方米的油漆费为80 元计算，需用多少钱？22．如图，线段AC=6cm，线段BC=15cm，点M是AC的中点，在CB上取一点N，使得CN：NB=1：2，求MN的长．23．尺规作图题（不写作图步骤，但保留作图痕迹）．已知：如图∠MON（1）求作：∠MON的平分线OC．（2）根据作法，请说明所作的射线OC就是∠MON的平分线OC．24．点A，O，B依次在直线MN上，如图1，现将射线OA绕点O顺时针方向以每秒10°的速度旋转，同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转，直线MN保持不动，如图2，设旋转时间为t秒（t≤12）．（1）在旋转过程中，当t=2时，求∠AOB的度数．（2）在旋转过程中，当∠AOB=105°时，求t的值．（3）在旋转过程中，当OA或OB是某一个角（小于180°）的角平分线时，求t 的值．参考答案一．选择题1．解：①∵直线AB和直线BA是同一条直线，∴①正确；②∵角是角，线是线，∴平角是一条直线，∴②错误；③两点之间，线段最短，∴③正确；④∵如果A、B、C三点不共线，则AB=BC不能得出点B是线段AC的中点，∴④错误．故选：B．2．解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，•与正方体三个剪去三角形交于一个顶点符合．故选：B．3．解：∵CB=4cm，DB=7cm，∴CD=7﹣4=3（cm）；∵D是AC的中点，∴AD=CD=3cm，∴AB=AD+DB=3+7=10（cm）．故选：C．4．解：∵三棱柱的展开图是两个三角形和三个长方形组成，∴该几何体是三棱柱．故选：B．5．解：3点30分相距2+=份，3点30分，此时钟面上的时针与分针的夹角是30×=75°．故选：C．6．解：∵∠1+∠2=180°∴∠1=180°﹣∠2又∵∠2+∠3=90°∴∠3=90°﹣∠2∴∠1﹣∠3=90°，即∠1=90°+∠3．故选：C．7．解：A．射线和直线不可测量，不能比较长短，故A错误；B．小于平角的角可分为锐角和钝角和直角三类，故B错误；C．有公共端点的两条射线组成的图形叫做角，故C错误；D．一个角的补角不一定比这个角大，故D正确．故选：D．8．解：A、长方体、正方体都是棱柱，故本选项不符合题意；B、圆锥和圆柱的底面都是圆，故本选项不符合题意；C、三棱柱的底面是三角形，故本选项不符合题意；D、六棱柱有18条棱、6个侧面、侧面为长方形，故本选项符合题意；故选：D．9．解：A、AC=BC，则点C是线段AB中点；B、AC+BC=AB，则C可以是线段AB上任意一点；C、AB=2AC，则点C是线段AB中点；D、BC=AB，则点C是线段A B中点．故选：B．10．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“A”与“0”是相对面，“B”与“3”是相对面，“C”与“﹣4”是相对面，∵相对面上的两数互为相反数，∴A、B、C内的三个数依次是0、﹣3、4．故选：A．11．解：∵OE平分∠BOD，∠BOE=23°，∴∠BOD=23°×2=46°；∵∠AOB是直角，∴∠AOD=90°﹣46°=44°，又∵OA平分∠COD，∴∠COD=2∠AOD=2×44°=88°，∴∠BOC=∠BOD+∠COD=46°+88°=134°．故选：B．12．解：根据题意得：第一层露出的表面积为：1×1×6﹣1×1=5，第二层露出的表面积为：1×1×6×4﹣1×1×13=11，第三层露出的表面积为：1×1×6×9﹣1×1×37=17，所以红色部分的面积为：5+11+17=33．方法2：立方体俯视图9：，前后左右视图各6格，红色部分的面积为9+6×4=33．故选：C．二．填空题（共6小题）13．解：∵礼物盒是一个有11个面的棱柱，∴侧面有11﹣2=9个，∴顶点数为9+9=18，故答案为：18．14．解：∠ABC=30°+90°=120°，故答案为：120°15．解：当OA与∠BOC的位置关系如图1所示时，∵OM是∠AOB的平分线，ON是∠BOC的平分线，∠AOB=80°，∠BOC=40°∴∠AOM=∠AOB=×80°=40°，∠BON=∠COB=×40°=20°，∴∠MON=∠BON﹣∠AOM=40°﹣20°=20°；当OA与∠BOC的位置关系如图2所示时，∵OM是∠AOB的平分线，ON是∠BOC的平分线，∠AOB=80°，∠BOC=40°∴∠BOM=∠AOB=×80°=40°，∠BON=∠BOC=×40°=20°，∴∠MON=∠BOM+∠BON=40°+20°=60°．故答案为：20°或60°．16．解：∵DA=6，DB=4，∴AB=DB+DA=4+6=10，∵C为线段AB的中点，∴BC=AB=×10=5，∴CD=BC﹣DB=5﹣4=1．故答案为：1．17．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“晋”与“祠”是相对面，“汾”与“酒”是相对面，“恒”与“山”是相对面．故答案为：祠．18．解：∵DE=AB=2cm，∴AB=2×5=10，∵E为BD的中点，∴BD=2DE=2×2=4cm，∴AD=AB﹣B D=10﹣4=6cm，∵AC=CD，∴CD=AD=×6=4m，∴CE=CD+DE=4+2=6cm．故答案为；6．三．解答题（共6小题）19．解：（1）∵OD是∠AOB的平分线，OE是∠BOC的平分线，∴∠AOD=∠BOD=∠BOC，∠BOE=∠COE=∠BOA，∵∠BOC=50°，∠BOA=80°，∴∠BOD=25°，∠BOE=40°，∴∠DOE=25°+40°=65°；（2）∵OD是∠AOB的平分线，OE是∠BOC的平分线，∴∠AOD=∠BOD=∠BOC，∠BOE=∠COE=∠BOA，∵∠AOC=150°，∴∠DOE=∠DOB+∠EOB=（∠BOC+∠BOA）=∠AOC=75°；（3）∠DOE=∠AOC；理由是：∵OD是∠AOB的平分线，OE是∠BOC的平分线，∴∠AOD=∠BOD=∠BOC，∠BOE=∠COE=∠BOA，∴∠DOE=∠DOB+∠EOB=（∠BOC+∠BOA）=∠AOC．20．解：如图，①连接AB，AC，②分别作线段AB，AC的垂直平分线，两垂直平分线相较于点P，则P即为售票中心．21．解：6×2.512×10×80=12057.6（元），答：需用12057.6元．22．解：∵M是AC的中点，∴MC=AM=AC=×6=3cm，又∵CN：NB=1：2∴CN=BC=×15=5cm，∴MN=MC+NC=3cm+5cm=8cm．23．解：（1）如图，射线OC是∠MON的平分线，（2）证明：如图，连接OC、BC、AC，根据作法可得BC=AC，OA=OB，在△OAC和△OBC中，∵∴△OAC≌△OBC（SSS），∴∠AOC=∠BOC，即射线OC是∠MON的平分线．24．解：（1）当t=2时，∠AOM=10°t=20°，∠BON=15°t=30°，所以∠AOB=180°﹣∠AOM﹣∠BON=130°；（2）当∠AOB=105°时，有两种情况：①10t+15t=180﹣105，解得：t=3；②10t+15t=180+105，解得：t=11.4；（3）①当OB是∠AON的角平分线时，10t+15t+15t=180，解得：t=4.5；②当OA是∠BOM的角平分线时，10t+10t+15t=180，解得：t=；③当OB是∠AOM的角平分线时，5t+20t=180，解得：t=9；④当OA是∠BON的角平分线时，10t+7.5t=180，解得：t=．。

第四章几何图形初步测试题一、选择题（本大题共10小题，每小题３分，共３０分）1.下列几何体中由三个面围成的是（）2．下列说法中错误的是（）A.直线AB和直线BA是同一条直线B.射线AB和射线BA是同一条射线C.线段AB和射线AB都是直线AB的一部分D.∠ABC和∠CBA表示同一个角3 .如图1所示，能折成棱柱的有()A.1个B.2个C.3个D.4个图14．下列角度换算不正确的是（）A. 5°16′=316′B. 10.2°=612′C. 72 000″=20°D. 18°25′=18.5°5．如图2，C，D是线段AB上的两点，D是AC的中点，AD=2.5 cm，AB=8 cm，则BC的长等于（）A. 2.5 cm B. 3 cm C. 3.5 cm D. 4 cm6.图3是由8个相同的小正方体堆砌而成的几何体，从上面看这个几何体的形状图的是（）A B C D7．过平面上Ａ，Ｂ，Ｃ三点中的任意两点作直线，共可以作（）A．1条Ｂ．3条Ｃ．1条或3条Ｄ．无数条8. 将如图4所示表面带有图案的正方体沿某些棱剪开展平后，得到的图形是（）A B C D 图49．甲、乙两人各用一张正方形的纸片ABCD折出一个45°的角（如图5），两人做法如下：甲：将纸片沿对角线AC折叠，使B点落在D点上，则∠1＝45°；乙：将纸片沿AM，AN折叠，分别使B，D落在对角线AC上的点P处，则∠MAN＝45°．对于两人的做法，下列判断正确的是（）A．甲乙都对B．甲对乙错C．甲错乙对D．甲乙都错图510.如图6，已知B在线段AC上，且BC=2AB，D，E分別是AB，BC的中点，有下列结论：①AB=31AC；②B是AE的中点；③EC=2BD；④DE=23AB.其中正确的结论有（）A.1个B.2个C.3个D.4个二、填空题（本大题共6小题，每小题3分，共18分）11. 在图7所示的横线上写出图中的几何体的名称．图712.经过刨平的木板上的两个点能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数知识是．图613. 如图8所示，三个正方体摆成一个几何体，则①是从 看的形状图，②是从 看 的形状图，③是从 看的形状图．图814.已知∠α与∠β互补，且∠α＞∠β，下列表示角的式子：①90°-∠β；②∠α-90°；③21（∠α＋∠β）；④21（∠α- ∠β）．其中能表示∠β的余角的是_________（填序号）.15. 一个棱柱有 12 个顶点，所有侧棱长的和是48 cm ，则每条侧棱长是 cm ．16. 一个正方体，六个面上分别写着六个连续整数，且每两个相对面上的两个数的和都相等，如图9所示，能 看到的所写的数为16，19，20，则这6 个整数的和为 ．图9三、解答题（本大题共6小题，共52分）17.（6分）一个角的补角比这个角的余角的2倍还多40°，求这个角的度数．18.（8分）如图10，货轮O 在航行过程中，在它的北偏东60°方向上，与之相距30海里处发现灯塔A ，同时 在它的南偏东30°方向上，与之相距20海里处发现货轮B ，在它的西南方向上发现客轮C ，按下列要求画出． （1）画出线段OB ； （2）画出射线OC ； （3）连接AB 交OE 于点D.图1019.（8分）图11是从正面、上面看由一些大小相同的小正方体搭成的几何体得到的平面图形． （1）这样的几何体只有一种情况吗？（2）若组成这个几何体的小正方体的块数为n ，请你写出n 的所有可能的值．图1120. （10分）如图12，小华用若干个正方形和长方形准备拼成一个长方体的表面展开图．拼完后，小华看来 看去总觉得所拼图形似乎存在问题．（1）请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全．（2）若图中的正方形边长为2 cm ，长方形的长为3 cm ，宽为2 cm ，请直接写出修正后所折叠而成的长方体的容积 cm 3（不计长方体容器的壁厚）.图12 21.（10分）如图13，已知C 是线段AB 的中点，E 是线段AB 上的点，D 是线段AE 的中点. （1）若线段AB =a ，CE =b ，且a ，b 满足｜a-15｜+（b-4.5）2=0，求a ，b 的值； （2）在（1）的条件下，求线段DE 的长； （3）若AB =15，AD =2BE ，求线段CE 的长.图1323.（12分）如图14-①，含30°角的直角三角尺的直角顶点O 在直线AB 上，OC ，OD 是三角尺的两条直角边，OE 平分∠AOD ．（1）若∠COE=20°，则∠BOD= ；若∠COE=α，则∠BOD= ．（用含α的式子表示）（2）当三角尺绕点O 逆时针旋转到图5-②的位置，其它条件不变，试猜测∠COE 与∠BOD 之间有怎样的数 量关系？并说明理由．BECD A图14附加题（20分）1.（6分）如图1，将三个三角形板直角顶点重叠在一起，公共的直角顶点为点B，若∠ABE=45°，∠GBH=30°，那么∠FBC的度数为（）A．30°B．25°C．20°D．15°2.（14分）围成立体图形的每个面都是平面，这样的立体图形叫多面体．仔细观察图２中所示的四面体、六面体、八面体，解决下列问题：（1）填空：①四面体的顶点数Ｖ＝，面数Ｆ＝，棱数Ｅ＝．②六面体的顶点数Ｖ＝，面数Ｆ＝，棱数Ｅ＝．③八面体的顶点数Ｖ＝，面数Ｆ＝，棱数Ｅ＝．（2）若将多面体的顶点数用Ｖ表示，面数用Ｆ表示，棱数用Ｅ表示，则Ｖ，Ｆ，Ｅ之间的数量关系可用一个公式来表示，这就是著名的欧拉公式．请写出欧拉公式：．（3）如果一个多面体的棱数为30，顶点数为20，那么这个多面体有多少个面？第四章 几何图形初步测试题参考答案一、1.B 2.B 3. B 4.D 5.B 6. C 7. C 8.C 9. A10. D 提示：由BC=2AB ，AC=AB+BC ，得AC=3AB ，故①正确；由E 分别是BC 的中点，BC=2AB ，得 BE=AB ，故②正确；由D ，E 分别是AB ，BC 的中点，得EC=BE=AB=2BD ，故③正确；由上述结论，得DE=DB+ BE=21AB+AB=23AB ，故④正确. 二、11. 圆锥 长方体 圆柱 球 五棱柱 12. 7 14 13. 正面 左面 上面 14.①②④ 15. 816. 111三、17. 解：设这个角为x°，则其余角为（90-x ）°，补角为（180-x ）°. 根据题意，得180-x=2（90-x ）+40，解得x=40． 答：这个角的度数是40°.18. 解： （1）（2）（3）如图1所示.图119. 解：（1）这样的几何体不只一种情况；（2）因为从上面看有5个正方形，所以最底层有5个正方体； 由正面看可得第2层最少有2个正方体，第3层最少有1个正方体； 由正面看可得第2层最多有4个正方体，第3层最多有2个正方体；所以该组合几何体最少有正方体5＋2＋1＝8（个），最多有正方体5＋4＋2＝11（个）. 所以n 可能为8，9，10或11．20. 解：（1）如图2所示，拼图存在问题，多了一块.图2（2）1221. 解：（1）由｜a-15｜+（b-4.5）2=0，得a-15=0，b-4.5=0，解得a =15，b =4.5. （2）由（1）知AB =15，CE =4.5. 因为C 是线段AB 的中点，所以AC=21AB=21×15=7.5，所以AE=AC+CE=7.5+4.5=12. 因为D 是线段AE 的中点，所以DE =21AE=21×12=6. （3）设BE =x ，由AD =2BE ，得AD =DE =2x .由AB =15，且AB=AD+DE+EB ，得5x =15，解得x =3，即BE=3. 因为C 是线段AB 的中点，所以BC=21AB=21×15=7.5，所以CE =BC-BE=7.5-3=4.5. 22.解：（1）40° 2α 提示：若∠COE=20°，因为∠COD=90°，∠COE=20°，所以∠EOD=90°-20°=70°．因为OE 平分∠AOD ，所以∠AOD=2∠EOD=140°，所以∠BOD=180°-140°=40°．若∠COE=α，则∠EOD=90-α．因为OE 平分∠AOD ，所以∠AOD=2∠EOD=2（90-α）=180-2α，所以∠BOD=180°-（180-2α）=2α．（2）∠BOD=2∠COE ，理由如下： 设∠BOD=β，则∠AOD=180°-β． 因为OE 平分∠AOD ，所以∠EOD=12∠AOD= 1802β-=90°-2β． 因为∠COD=90°，所以∠COE=90°-（90°-2β）= 2β，即∠BOD=2∠COE ． 附加题1. D 提示：∵∠ABE=45°，∴∠CBE=45°，∴∠CBG=45°，∵∠GBH=30°，∴∠FBG=60°，∴∠FBC=∠FBG- ∠CBG=60°-45°=15°．2. （1）①4 4 6 ②8 6 12 ③6 8 12 （2）Ｖ＋Ｆ－Ｅ＝２（3）由欧拉公式可知，E=30，V=20，可得面数F=12.所以这个多面体有12个面．。

人教版七年级上册第四章几何图形初步单元检测试题（含答案）一、单选题（共10题；共30分）1.如图，图中的长方形共有（）个．A. 9B. 8C. 5D. 42.如图所示几何图形中，是棱柱的是（）A. B. C. D.3.如图，是一个几何体的表面展开图，则该几何体是（）A. 正方体B. 长方体C. 三棱柱D. 四棱锥4.如图，∠AOC＞∠BOD，则（）A. ∠AOB＞∠CODB. ∠AOB=∠CODC. ∠AOB＜∠CODD. 以上都有可能5.如图所示，∠AOC=∠BOD=90°，若∠AOB=150°，则∠DOC的度数为（）A. 30°B. 40°C. 50°D. 60°6.如图，线段CD在线段AB上，且CD=2，若线段AB的长度是一个正整数，则图中以A，B，C，D这四点中任意两点为端点的所有线段长度之和可能是（）A. 28B. 29C. 30D. 317.将一个圆分割成四个大小相同的扇形，则每个扇形的圆心角是（）度．A.45B.60C.90D.1208.若∠AOB=90°，∠BOC=40°，则∠AOC的度数为（）A. 50°B. 50°或120°C. 50°或130°D. 130°9.直棱柱的侧面都是（）A. 正方形B. 长方形C. 五边形D. 菱形10.如果时钟上的时针、分针和秒针都是匀速地转动，那么从3时整（3:00）开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有( )A. 1次B. 2次C. 3次D. 4次二、填空题（共8题；共24分）11.已知∠α=36°14′25″，则∠α的余角的度数是________．12.如果一个六棱柱的一条侧棱长为5cm，那么所有侧棱之和为________ cm13.（1）102°43′32″+77°16′28″=________；（2）98°12′25″÷5=________．14.如图，∠AOB中，OD是∠BOC的平分线，OE是∠AOC的平分线，若∠AOB=135°，则∠EOD=________°．15.（1）32°43′30″=________°；（2）86.47°=________ °________′________″16.已知：点A、B、C在同一直线上，若AB=12cm，BC=4cm，且满足D、E分别是AB、BC 的中点，则线段DE的长为________cm．17.用棱长是1cm的小正方体组成如图所示的几何体，把这个几何体放在桌子上，并把暴露的面涂上颜色，那么涂颜色面的面积之和是________cm2.18.用平面截几何体可得到平面图形，在表示几何体的字母后填上它可截出的平面图形的号码．如A（1、5、6）；则B（________）；C（________）；D（________）；E（________）．三、解答题（共6题；共42分）19.如图，OC平分∠BOD，∠AOD=110°，∠COD=35°，求∠AOB的度数．20.直线AB、CD相交于点O，OE平分∠AOD，∠FOC=90°，∠1=40°，求∠2与∠3的度数。

几何图形初步单元测试卷一、选择题（本题共计12 小题，每题分，共计36分，）1. 下列图形中，不是立体图形的是（）A.棱柱B.圆锥C.正方形D.长方体2. 如图所示的棱柱有（）A.个面B.个面C.条棱D.条棱3. 如图，是一直角，，平分，则等于（）A. B. C. D.4. 如图，，是内部任意一条射线，、分别是、的角平分线，下列叙述正确的是（）A.的度数不能确定B.C. D.5. 已知，那么的余角为（）A. B. C. D.6. 下列语句错误的是（）A.锐角的补角一定是钝角B.一个锐角和一个钝角一定互补C.互补的两角不能都是钝角D.互余且相等的两角都是7. 有同样大小的立方体个，把它们竖个，横个，紧密地没有缝隙地搭成一个大的立方体（如右图），如果用根坚硬笔直的细铁丝扎进这个大立方体，最多可以穿透几个小立方体（）A.个B.个C.个D.个8. 下列结论不正确的是（）A.正方体和长方体都是四棱柱B.棱柱的侧面个数与底面图形的边数一样C.三棱柱的侧面是三角形D.六棱柱的侧面是四边形9. 已知：，，，下列结论正确的是（）A. B.C. D.三个角互不相等10. 下列说法正确的是（）A.在墙上固定一根木条，至少需要颗钉子B.射线和射线是同一条射线C.延长直线D.线段和线段不是同一条线段11. 下列说法正确的有（）个①连接两点的线段的长叫两点之间的距离；②直线比线段长；③若，则为的中点；④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形．A. B. C. D.12. 把一副三角板按如图方式的位置摆放，则形成两个角，设分别是，，若，则A. B. C. D.二、填空题（本题共计6 小题，每题分，共计18分，）13. 有时需要把弯曲的河流改直，以达到缩短航程的目的，这样做的依据是________．14. 如图，在利用量角器画一个的的过程中，对于先找点，再画射线这一步骤的画图依据，小华认为是两点确定一条直线，小阳认为是两点之间线段最短．你认为________同学的说法是正确的．15. 长方形铁片绕它的一边快速旋转一周，形成一个________体．16. 如图，已知线段，线段，是线段的中点，是线段的中点，则线段长为________．17. 如图，图中有________条直线，有________条射线，有________条线段，以为顶点的角有________个．18. 今天晚上九点半安庆电人教版七年级数学上册第四章几何图形初步单元测试题一、选择题(本大题共6小题，每小题4分，共24分；在每小题列出的四个选项中，只有一项符合题意)1．如图1所示，已知O是直线AB上一点，∠1＝70°，则∠2的度数是()图1A．20°B．70°C．110°D．130°2．如图2，将一个圆柱体放置在长方体上，其中圆柱体的底面直径与长方体的宽相等，则从该立体图形的左面看得到的图形是()图2图33．下列说法正确的是()A．过两点有一条或两条直线B．连接两点的线段叫这两点的距离C．两点之间，直线最短D．若点C在线段AB外，则AC＋BC＞AB4．如图4，直线AB，CD相交于点O，∠AOE＝90°，OF平分∠AOE，∠1＝15°30′，则下列结论中不正确的是()图4A．∠2＝45°B．∠1＝∠3C．∠AOD与∠1互为补角D．∠1的余角等于75°30′5．已知线段AB＝9 cm，在直线AB上画线段BC，使BC等于3 cm，则线段AC的长为()A．12 cm B．6 cmC．12 cm或6 cm D．9 cm或12 cm6．在上午9时到10时之间，时钟的分针与时针会重合一次，这次的重合所在时间是()A．9：48～9：49 B．9：49～9：50C．9：50～9：51 D．9：51～9：52二、填空题(本大题共6小题，每小题4分，共24分)7．若∠α＝32°22′，则∠α的余角的度数为________．8．若∠α＝37°49′40″，∠β＝52°10′20″，则∠β－∠α＝________．9．将一副三角尺叠放在一起，使直角顶点重合于点O，绕着点O任意转动其中一个三角尺，得到如图5所示的图形，则与∠AOD始终相等的角是________．图510．如图6所示，C是线段AB的中点，D是线段BC的中点，若AB＝6 cm，则AD的长是________cm.图611．如图7，已知OC与AB相交于点O，且∠AOC＝90°，OD平分∠AOC，OE平分∠AOD，则∠BOE＝________度．图712．如图8是一个长方体的展开图，其中四边形ABCD是正方形，则原长方体的体积是________．图8三、解答题(本大题共6小题，共52分)13．(6分)如图9，已知A，B，C三点．(1)画直线AC；(2)画射线BC；(3)画线段AB.图914．(6分)一个角的余角比它的补角的23还少40°，求这个角的度数．15．(8分)如图10所示，∠AOB ＝130°，OC 平分∠AOB ，∠BOD 是直角．求∠COD 的度数．图1016．(10分)如图11，线段AB ＝8 cm ，C 是线段AB 上一点，AC ＝3.2 cm ，M 是AB 的中点，N 是AC 的中点．(1)求线段CM 的长； (2)求线段MN 的长．图1117．(10分)一只小虫从点A出发向北偏西15°方向爬行3 cm到点B处，再从点B出发向南偏东75°方向爬行3 cm到点C处．(1)试画图确定A，B，C三点的位置；(2)从图上量出点C到点A的距离；(3)指出点C在点A的什么方向．18．(12分)如图12，数轴的原点为O，A，B，C是数轴上的三点，点B对应的数为1，AB＝6，BC＝2，动点P，Q分别从点A，C同时出发，分别以每秒2个单位长度和每秒1个单位长度的速度沿数轴正方向运动．设运动时间为t秒(t＞0)．(1)求点A，C对应的数；(2)求点P，Q对应的数(用含t的式子表示)；(3)当t为何值时，OP＝OQ?图121． C 2．A 3． D 4． D 5． C 6． B 7．[答案] 57°38′ 8．[答案] 14°20′40″ 9．[答案] ∠BOC 10．[答案] 4.5 11．[答案] 157.5 12．[答案] 12 cm 3 13．解：如图所示．14．解：设这个角的度数为x °，根据题意，得 90－x ＝23(180－x)－40.解得x ＝30.所以这个角的度数是30°.15．解：因为∠AOB ＝130°，OC 平分∠AOB ， 所以∠BOC ＝12∠AOB ＝65°.因为∠BOD 是直角，即∠BOD ＝90°，所以∠COD ＝∠BOD －∠BOC ＝90°－65°＝25°.16． (1)根据M 是AB 的中点，求出AM ，再利用CM ＝AM －AC 求得线段CM 的长； (1)根据N 是AC 的中点求出NC 的长度，再利用MN ＝CM ＋NC 即可求出MN 的长度． 解：(1)由AB ＝8 cm ，M 是AB 的中点，得AM ＝4 cm.又因为AC ＝3.2 cm ， 所以CM ＝AM －AC ＝4－3.2＝0.8(cm)， 即线段CM 的长为0.8 cm.(2)因为N 是AC 的中点，所以NC ＝1.6 cm. 所以MN ＝NC ＋CM ＝1.6＋0.8＝2.4(cm)， 即线段MN 的长为2.4 cm. 17．解：(1)如图．(2)3 cm.(3)东北方向或北偏东45°方向．18．解：(1)因为点B 对应的数为1，AB ＝6，BC ＝2， 所以点A 对应的数是1－6＝－5，点C 对应的数是1＋2＝3.(2)因为动点P ，Q 分别从点A ，C 同时出发，分别以每秒2个单位长度和1个单位长度的速度沿数轴正方向运动，所以点P 对应的数是－5＋2t ，点Q 对应的数是3＋t.(3)①若点P 与点Q 在原点两侧，则5－2t ＝3＋t ，解得t ＝23；②若点P 与点Q 在人教版七年级上册数学单元知识检测题：第四章几何图形初步一、选择题1.如图，它需再添一个面，折叠后才能围成一个正方体，下列选项中的黑色小正方形分别由四位同学补画，其中正确的是( )A. B. C. D.2.下列图形不是正方体展开图的是( )A. B. C.D.3.如图，在直线l上依次有A，B，C三点，则图中线段共有（）A. 4 条B. 3 条C. 2 条D. 1 条4.如图是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的字是（）A. 美B. 丽C. 揭D. 东5.如果线段AB=6 cm，BC=4 cm，且线段A、B、C在同一直线上，那么A、C间的距离是( )A. 10 cmB. 2 cmC. 10 cm或2 cmD. 无法确定6.如图，点A，B，C都在直线a上，下列说法错误的是( )A. 点A在射线BC上B. 点C在直线AB上C. 点A在线段BC上D. 点C 在射线AB上7.已知线段AB=8，延长线段AB至C，使得BC= AB，延长线段BA至D，使得AD= AB，则下列判断正确的是（）A. BC= ADB. BD=3BCC. BD=4ADD. AC=6AD8.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于（）A. 50°B. 130°C. 40°D. 140°9.如图，∠AOC=∠BOD=90°，∠A0D=140°，则∠BOC的度数为（）A. 30°B. 45°C. 50°D. 40°10.若∠A，∠B互为补角，且∠A＝130°，则∠B的余角是（）A. 40°B. 50°C. 60°D. 70°11.如图，直线m外有一点0，A是m上一点，当点A在m上运动时，有( )A. >B. =C. ＜D. ＞、= 、＜都有可能12.已知线段AB的长为4，点C为AB的中点，则线段AC的长为（）A. 1B. 2C. 3D. 4二、填空题13.若正方体棱长的和是36，则它的体积是________．14.用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②三棱锥；③圆柱；④圆锥________（写出所有正确结果的序号）．15.在朱自清的《春》中有描写春雨“像牛毛，像细丝，密密地斜织着”的语句，这里把雨看成了线，这说明________．16.要把木条固定在墙上至少需要钉________颗钉子，根据是________．17.已知点A、B、C在同一条直线上，且线段AB＝5，BC＝4，则A、C两点间的距离是________．18.已知A、B、C三点在一条直线上，且线段AB＝15cm，BC＝5cm，则线段AC＝________．19.已知∠1=60°，则∠1的余角的补角度数是________20.已知一个角的补角比它余角的2倍还大45°，则这个角的度数为________ 。

第四章几何图形初步一、选择题1.角是指（）A. 由两条线段组成的图形B. 由两条射线组成的图形C. 由两条直线组成的图形D. 有公共端点的两条射线组成的图形2.如果一个角的补角是150°，那么这个角的余角的度数是（）A. 30°B. 60°C. 90°D. 120°3.下列说法正确的是（）A. 经过两点有且只有一条线段B. 经过两点有且只有一条直线C. 经过两点有且只有一条射线D. 经过两点有无数条直线4.如图，四条线段中，最短和最长的一条分别是（）A. acB. bdC. adD. bc5.如图，B在线段AC上，且BC=2AB，D，E分别是AB，BC的中点．则下列结论：①AB= AC；②B是AE的中点；③EC=2BD；④DE=AB．其中正确的有（）A. 1个B. 2个C. 3个D. 4个6.已知∠α=70°，则∠α的补角为（）A. 120°B. 110°C. 70°D. 20°7.下列语句中，正确的是（）．A. 比直角大的角钝角;B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角8.如图，已知AD平分∠BAE，若∠BAD=62°，则∠CAE的度数是（）A. 55°B. 56°C. 58°D. 62°9.如图，下列关系式中与图不符合的式子是（）A. AD-CD=AB+BCB. AC-BC=AD-BDC. AC-BC=AC+BDD. AD-AC=BD-BC10.如图是一个正方体的平面展开图，当把它拆成一个正方体，与空白面相对的字应该是（）A. 北B. 京C. 欢D. 迎二、填空题11.已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC=________.12.若∠α=32°22′，则∠α的余角的度数为________．13.已知一个角的补角等于155°，则这个角的余角等于________14.八棱柱有________个顶点，________条棱，________个面．15.和互补，且-=50°，求和的度数． ________、 ________16.34.42°=________（用度、分、秒表示）.17.一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=________ °．18.用一个平面去截长方体，截面________是平行四边形（填“可能”或“不可能”）．19.一条直线上有A、B、C三个点，AB=7cm，BC=4cm，则AC=________ ．20.已知线段AB=1996，P、Q是线段AB上的两个点，线段AQ=1200，线段BP=1050，则线段PQ=________．三、解答题21.已知∠BOC＝120°，∠AOB＝70°，求∠AOC的大小。

人教版七年级上册数学第四章《几何图形初步》检测卷（时间：90分钟满分：120分）一、选择题（每小题3分，共30分）1. 下列第一行的四个图形，每个图形均是由四种简单的图形a，b，c，d（圆、直线、三角形、长方形）中的两种组成.例如，由a，b组成的图形记作a⊙b，那么由此可知，下列选项的图形，可以记作a ⊙d的是（）2. 如图4-1，该几何体从正面看得到的平面图形是（）图4-13. 对于直线AB、线段CD、射线EF，其中能相交的图是（）4. 下列现象：（1）用两个钉子就可以把木条固定在墙上；（2）从A地到B地架设电线，总是尽可能沿着线段AB架设；（3）植树时，只要确定两棵树的位置，就能确定同一行树所在的直线；（4）把弯曲的公路改直，就能缩短路程.其中能用“两点确定一条直线”来解释的现象是（）A.（1）（2）B.（1）（3）C.（2）（4）D.（3）（4）5. 如图4-2，AB=12，C为AB的中点，点D在线段AC上，且AD∶CB=1∶3，则线段DB的长度为（）图4-2A.4B.6C.8D.106. 已知线段AB和点P，如果P A+PB=AB，那么（）A.P为AB的中点B.点P在线段AB上C.点P在线段AB外D.点P在线段AB的延长线上7. 学校、书店、邮局在平面图上的标点分别是A，B，C，书店在学校的正东方向，邮局在学校的南偏西25°，那么平面图上的∠CAB 等于（）A.25°B.65°C.115°D.155°8. 若∠1=40.4°，∠2=40°4′，则∠1与∠2的关系是（）A.∠1=∠2B.∠1＞∠2C.∠1＜∠2D.以上都不对图4-39. 如图4-3，∠AOB=130°，射线OC是∠AOB内部任意一条射线，OD，OE分别是∠AOC，∠BOC的平分线，下列叙述正确的是（）A.∠DOE的度数不能确定B.∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°C.∠BOE=2∠COD∠EOCD.∠AOD=1210. 如图4-4，OD⊥AB于点O，OC⊥OE，图中与∠AOC互补的角有（）图4-4A.1个B.2个C.3个D.4个二、填空题（每小题4分，共32分）11.夏天，快速转动的电扇叶片，给我们一个完整的平面的感觉，说明_____.12.如图4-5，C，D是线段AB上的两点，若AC=4，CD=5，DB=3则图中所有线段长度的和是_____.图4-513.已知∠A=100°，那么∠A的补角是_____.14.时钟上3点40分时分针与时针夹角的度数为____.15.如图4-6，O在直线AB上，∠AOD=90°，∠COE=90°，则图中相等的锐角有_____对.图4-616.已知∠AOC和∠BOD都是直角，如果∠AOB=150°，那么∠COD 的度数为_____.17.如图4-7，一个正方体的表面上分别写着连续的6个整数，且每两个相对面上的两个数的和都相等，则这6个整数的和为_____.图4-718.平面内有四个点A，B，C，D，过其中每两个点画直线可以画出的直线有_____.三、解答题（共58分）19.（8分）计算：（1）22°18′×5；（2）90°-57°23′27″.20.（8分）把图4-8的展开图和它们的立体图形连起来.图4-821.（10分）如图4-9，已知线段a，b，c，用圆规和直尺画图.（不用写作法，保留画图痕迹）（1）画线段AB，使得AB=a+b-c；（2）在直线AB外任取一点K，画射线AK和直线BK；（3）反向延长AK至点P，使AP=KA，画线段PB，比较所画图形中线段P A与BK长度的和与线段AB长度的大小.图4-922.（10分）如图4-10，已知线段AB和CD的公共部分BD=13AB=14CD，线段AB，CD的中点E，F之间的距离是10 cm，求线段AB，CD的长度.图4-1023.（10分）如图4-11（1），已知直角三角形两直角边的长分别为3和4，斜边的长为5.（1）试计算该直角三角形斜边上的高；（2）按如图4-11（2），4-11（3），4-11（4）三种情形计算该直角三角形绕某一边旋转得到的立体图形的体积.（结果保留π）图4-1124.（12分）如图4-12，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°.（1）请你数一数，图中有多少个小于平角的角；（2）求出∠BOD的度数；（3）请通过计算说明OE是否平分∠BOC.图4-12人教版七年级上册数学第四章《几何图形初步》检测卷答案一、1.A 解析：根据题意，知a代表长方形，d代表直线，所以记作a⊙d的图形是长方形和直线的组合.故选A.2. A3. B 解析：A.直线AB与线段CD不能相交，故此选项不符合题意；B.直线AB与射线EF能相交，故此选项符合题意；C.射线EF与线段CD不能相交，故此选项不符合题意；D.直线AB与射线EF不能相交，故此选项不符合题意.故选B.4. B 解析：（1）用两个钉子就可以把木条固定在墙上，根据是两点确定一条直线；（2）从A地到B地架设电线，总是尽可能沿着线段AB架设，根据是两点之间，线段最短；（3）植树时，只要确定两棵树的位置，就能确定同一行树所在的直线，根据是两点确定一条直线；（4）把弯曲的公路改直，就能缩短路程，根据是两点之间，线段最短.故选B.5. D 解析：因为C为AB的中点，AB=12，所以AC=BC=12AB=12×12=6.因为AD∶CB=1∶3，所以AD=2，所以DB=AB-AD=12-2=10.故选D.6. B 解析：如图D4-1.因为P A+PB=AB，所以点P在线段AB上.故选B.图D4-17. C 解析：如图D4-2.由图可知，∠CAB=∠1+∠2=25°+90°=115°.故选C.图D4-28. B 解析：因为∠1=40.4°=40°24′，∠2=40°4′，所以∠1＞∠2.故选B.9. B 解析：因为OD，OE分别是∠AOC，∠BOC的平分线，所以∠AOD=∠COD，∠EOC=∠BOE.又因为∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°，所以∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°.故选B.10. B 解析：根据题意，得（1）因为∠AOC+∠BOC=180°，所以∠BOC与∠AOC互补.（2）因为OD⊥AB，OC⊥OE，所以∠EOD+∠DOC=∠BOC+∠DOC=90°，所以∠EOD=∠BOC，所以∠AOC+∠EOD=180°，所以∠EOD与∠AOC互补，所以图中与∠AOC互补的角有2个.故选B.二、11.线动成面12. 41 解析：AD=AC+CD=9，AB=AC+CD+DB=12，CB=CD+DB=8，故题图中所有线段长度的和为AC+AD+AB+CD+CB+DB=41.13. 80°14. 130°解析：3点40分时分针与时针夹角的度数为30°×=130°.4+1315. 2 解析：因为∠AOD=90°，所以∠AOC+∠COD=90°.因为∠COE=90°，所以∠COD+∠DOE=90°，所以∠AOC=∠DOE.因为∠BOD=180°-∠AOD=90°，所以∠DOE+∠BOE=90°，所以∠BOE=∠COD.故图中相等的锐角有2对.16. 30°或150°解析：如图D4-3（1），因为∠BOD=90°，∠AOB=150°，所以∠AOD=60°.又因为∠AOC=90°，所以∠COD=30°.如图D4-3（2），因为∠BOD=90°，∠AOC=90°，∠AOB=150°，所以∠AOD=60°，所以∠COD=150°.综上所述，∠COD的度数为30°或150°.图D4-317. 51 解析：因为正方体的表面展开图，相对的面一定相隔一个正方形，所以6若不是最小的数，则6与9是相对面.因为6与9相邻，所以6是最小的数，所以这6个整数的和为6+7+8+9+10+11=51. 18. 1条、4条或6条解析：如果A，B，C，D四点在同一直线上，那么只能确定一条直线，如图D4-4（1）；如果4个点中有3个点（不妨设点A，B，C）在同一直线上，而第4个点，点D不在此直线上，那么可以确定4条直线，如图D4-4（2）；如果4个点中，任何3个点都不在同一直线上，那么点A分别和点B，C，D确定3条直线，点B分别与点C，D确定2条直线，最后点C，D确定一条直线，这样共确定6条直线，如图D4-4（3）.综上所述，过其中每2个点可以画1条、4条或6条直线.（1）（2）（3）图D4-4三、19.解：（1）22°18′×5=110°90′=111°30′.（2）90°-57°23′27″=32°36′33″.20. 解：如图D4-5.图D4-521. 分析：（1）首先作射线CE在射线CE上截取CD=a，BD=b，再在CB上截取AC=c，则可得出AB=a+b-c；（2）根据射线和直线的概念过点K即可作出；（3）根据AP=AK，利用两点之间线段最短即可得出答案.解：（1）如图D4-6（1）.（2）如图D4-6（2）.（1）（2）（3）图D4-6（3）如图D4-6（3）.因为AP=KA，所以线段P A与BK长度的和大于线段AB的长度. 22. 解：设BD=x cm，则AB=3x cm，CD=4x cm，AC=6x cm.因为E，F分别为线段AB，CD的中点，所以AE=12AB=1.5x（cm），CF=12CD=2x（cm）.所以EF=AC-AE-CF=6x-1.5x-2x=2.5x（cm）. 因为EF=10 cm，所以2.5x=10，解得x=4.所以AB=12 cm，CD=16 cm.23. 解：（1）三角形的面积为12×5h=12×3×4，解得h= 12/5.（2）在图4-11（2）中，所得立体图形的体积为13π×32×4=12π；在图4-11（3）中，所得立体图形的体积为13π×42×3=16π；在图4-11（4）中，所得立体图形的体积为13π×（125）2×5=485π.24. 解：（1）图中小于平角的角有∠AOD，∠AOC，∠AOE，∠DOC，∠DOE，∠DOB，∠COE，∠COB，∠EOB，共9个.（2）因为∠AOC=50°，OD平分∠AOC，所以∠DOC=1/2∠AOC=25°，∠BOC=180°-∠AOC=130°.所以∠BOD=∠DOC+∠BOC=155°.（3）因为∠DOE=90°，∠DOC=25°，所以∠COE=∠DOE-∠DOC=90°-25°=65°.又因为∠BOE=∠BOD-∠DOE=155°-90°=65°，所以∠COE=∠BOE，即OE平分∠BOC.。