数学分析复习练习题(1)

一、填空题1. 2.;3. (0) =_____；4.5.6.二、选择题1．下列函数在给定区间上不满足拉格朗日中值定理的有（）。

A； B. ；C； D.2( )是错误的．A BC D3）．A BC．D4）。

A. 极大值点B. 极小值点C. 驻点D.以上都不对5（）(A) (B) ；(D)6（）(A) 连续点；(B) 可去间断点；(C) 跳跃间断点；(D) 第二类间断点。

7）(A)(B)(C)(D)8（ ）(B)9（ ）(A)(B) (C) (D)三、解答题12n ++22d y3．4四、1.2.证明:3.,.五、1. （1（2（32.六、一、填空题1.2.3. 0，1）内的无理数｝，其上下确界分别为______ ；4. 的全体聚点为;5.6.78.相切，则;910..二、选择题1.设）(A)无穷小量 (B)任意小的正数 (C)常量 (D)给定的正数2.处（ ）. （A ）取得极大值 （B ）取得极小值（C（D ）可能有极值，也可能有拐点。

3.） (A) 1 (B)-1 (C) 0 (D) 以上都不对. 4.(A) 在任意区间[a,b]上罗尔定理成立；（B ）在[0,8]上罗尔定理不成立；（C ）在[0,8]上罗尔定理成立； (D)在任意闭区间上罗尔定理不成立. 5.）． (A)有定义且有极限；(B)无定义但有极限； (C)有定义但无极限； (D)无定义且无极限 6.（ ） (A) 连续点； (B) 跳跃间断点； (C)可去间断点； (D) 第二类间断点。

7.（ ）(C)8.（） (A) 没有根； (B) 最多有两个根； (C) 有且仅有三个根； (D) 有四个根。

9）(A) 单调增； (B) 单调减； (C) 有极大值； (D) 有极小值。

10（ ） (A)(C)以上都不对。

三、解答题2.3.4. 求极限5. 求极限. 6.7. 求极限8. 求极限四、1. 证明2..3.4.5.6证明:78.五、1（1（22证明（1（2六、1..2.用有限覆盖定理或者用闭区间套定理证明根的存在定理。

数学分析基础试题及答案一、选择题（每题10分，共50分）1. 设函数f(x)在点x=0处连续，且f(0)=1，则下列选项正确的是（）A. 函数f(x)在x=0处可导B. 函数f(x)在x=0处不可导C. 函数f(x)在x=0处可导，且导数为1D. 函数f(x)在x=0处可导，且导数不为1答案：C2. 设函数y=f(x)在区间(a, b)内可导，且f'(x) > 0，则下列选项正确的是（）A. 函数f(x)在区间(a, b)内单调增加B. 函数f(x)在区间(a, b)内单调减少C. 函数f(x)在区间(a, b)内无单调性D. 无法确定函数f(x)的单调性答案：A3. 下列函数中，哪一个函数在区间(0, +∞)内连续但不可导？（）A. y=|x|B. y=x^2C. y=x^3D. y=x^4答案：A4. 设函数f(x)在区间(a, b)内连续，且f(a)=f(b)，则下列选项正确的是（）A. 存在c∈(a, b)，使得f(c)=0B. 存在c∈(a, b)，使得f'(c)=0C. 函数f(x)在区间(a, b)内单调D. 函数f(x)在区间(a, b)内无单调性答案：B5. 设函数f(x)在区间(a, b)内可导，且f'(x) < 0，则下列选项正确的是（）A. 函数f(x)在区间(a, b)内单调增加B. 函数f(x)在区间(a, b)内单调减少C. 函数f(x)在区间(a, b)内无单调性D. 无法确定函数f(x)的单调性答案：B二、填空题（每题10分，共50分）6. 设函数f(x)在区间(a, b)内连续，且f(a)=f(b)，则根据介值定理，存在c∈(a, b)，使得f(c)=______。

答案：07. 函数f(x)=x^3在x=1处的导数为______。

答案：38. 设函数f(x)在区间(a, b)内可导，且f'(x) > 0，则函数f(x)在区间(a, b)内______。

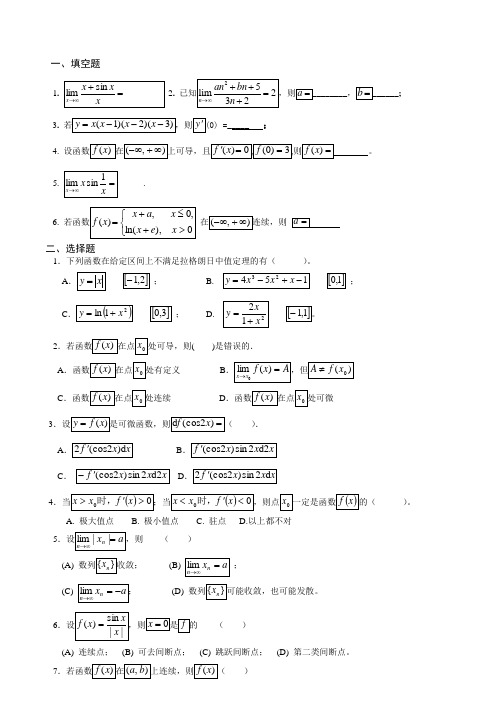
一、填空题1. _______sin lim =+∞→xxx x 2. 已知25lim232n an bn n →∞++=+，则a =________，b =______; 3. 若)3)(2)(1(---=x x x x y ，则y '(0) =_____；4. 设函数)(x f 在),(∞+-∞上可导，且0)(='x f ,3)0(=f ,则=)(x f 。

5. =∞→xx x 1sinlim ______. 6. 若函数⎩⎨⎧>+≤+=0),ln(,0,)(x e x x a x x f 在),(∞+-∞连续，则 =a二、选择题1．下列函数在给定区间上不满足拉格朗日中值定理的有（ ）。

A ．x y = []2,1- ； B. 15423-+-=x x x y []1,0 ；C ．()21ln xy += []3,0 ； D. 212xxy +=[]1,1-。

2．若函数)(x f 在点0x 处可导，则( )是错误的．A ．函数)(x f 在点0x 处有定义B ．A x f x x =→)(lim 0，但)(0x f A ≠C ．函数)(x f 在点0x 处连续D ．函数)(x f 在点0x 处可微 3．设)(x f y =是可微函数，则=)2(cos d x f （ ）． A ．x x f d )2(cos 2' B ．x x x f d22sin )2(cos ' C ． x x x f d22sin )2(cos '- D ．x x x f d 2sin )2(cos 2'4．当()00>'>x f x x 时，；当()00<'<x f x x 时，，则点0x 一定是函数()x f 的（ ）。

A. 极大值点B. 极小值点C. 驻点D.以上都不对 5．设a x n n =∞→||lim ，则 （ ）(A) 数列}{n x 收敛； (B) a x n n =∞→lim ；(C) a x n n -=∞→lim ； (D) 数列}{n x 可能收敛，也可能发散。

数学分析习题集第一篇：函数极值与最值1. 求函数 $f(x)=2x^3-6x^2-12x+20$ 的极值。

2. 求函数 $f(x)=\dfrac{1}{x^2+2x+3}$ 的最大值和最小值。

3. 求函数 $f(x)=\ln\left(x^2-2x+3\right)$ 的最大值和最小值。

4. 求函数 $f(x)=\sqrt{2-x-x^2}$ 的最大值和最小值。

5. 求函数 $f(x)=\dfrac{x}{1-x}$ 在 $(-\infty,1)$ 上的最大值和最小值，并说明在何处取得。

6. 已知函数 $y=\sin x+\cos x$，求其最大值和最小值。

7. 已知函数 $y=x^3-3x+2$，求其极值和最值。

8. 求函数 $f(x)=\sin x\cos x+\dfrac{1}{4}$ 的最大值和最小值。

9. 求函数 $f(x)=\dfrac{x^3}{3}-\dfrac{x^2}{2}+x$ 在 $[-1,2]$ 上的最大值和最小值。

10. 求函数 $f(x)=\dfrac{x^2}{x+1}$ 的最大值和最小值。

第二篇：导数与微分1. 求函数 $f(x)=\dfrac{x^2}{x+1}$ 在 $x=2$ 处的导数和微分。

2. 求函数 $f(x)=\ln\left(x^2-2x+3\right)$ 在$x=1$ 处的导数和微分。

3. 求函数 $f(x)=\sin 2x$ 在 $x=0$ 处的导数和微分。

4. 求函数 $f(x)=\sqrt{x^2+1}$ 在 $x=2$ 处的导数和微分。

5. 求函数 $f(x)=\dfrac{1}{x^2-5x+6}$ 在 $x=1$ 处的导数和微分。

6. 求函数 $f(x)=\dfrac{\cos x}{1+\sin x}$ 在$x=\dfrac{\pi}{4}$ 处的导数和微分。

7. 求函数 $f(x)=\ln\left(\dfrac{x^2}{1-x}\right)$ 在 $x=0$ 处的导数和微分。

数学分析练习题数学分析练习题数学分析是一门重要的数学学科，它研究的是数学中的极限、连续、微分、积分等概念和性质。

通过学习数学分析，我们可以更好地理解和应用数学知识。

而练习题则是巩固和应用所学知识的重要方式。

在这篇文章中，我们将探讨一些数学分析的练习题，帮助读者更好地理解和应用相关概念。

一、极限练习题1. 计算极限：lim(x→0) (sinx/x)。

这是一个经典的极限问题，可以通过泰勒级数展开或利用极限的定义来求解。

通过这个练习题，我们可以加深对极限的理解，并熟悉不同的求解方法。

2. 证明极限：lim(x→∞) (1+1/x)^x = e。

这是一个重要的极限关系，它揭示了自然对数e与指数函数的联系。

通过证明这个极限，我们可以深入理解e的定义和性质。

二、连续性练习题1. 设函数f(x) = x^2，证明f(x)在区间[0,1]上是连续的。

通过证明函数的连续性，我们可以理解连续函数的性质和重要定理，如介值定理和零点定理。

2. 设函数f(x) = |x|，证明f(x)在整个实数轴上是连续的。

这是一个稍微复杂一些的例子，通过证明绝对值函数的连续性，我们可以进一步理解不同类型函数的连续性。

三、微分练习题1. 求函数f(x) = x^3的导数。

通过求解导数，我们可以熟悉微分的定义和基本运算法则，并掌握求解各种函数的导数的方法。

2. 求函数f(x) = e^x的高阶导数。

通过求解高阶导数，我们可以进一步理解指数函数的性质，并学习应用泰勒级数展开来求解复杂函数的导数。

四、积分练习题1. 计算定积分：∫(0,1) x^2 dx。

通过计算定积分，我们可以熟悉积分的定义和基本运算法则，并理解定积分的几何意义。

2. 计算不定积分：∫(x^2+2x) dx。

通过计算不定积分，我们可以掌握积分的基本运算法则，并学习应用不定积分解决实际问题。

通过以上练习题的学习和解答，我们可以加深对数学分析概念和性质的理解，提高数学分析的应用能力。

第二章 数列极限一、填空题1．∑=∞→=++++Nn n n1 (3211)lim_________；2．-+∞→3(lim n n n3．=++++++++∞→n nn 31913112141211lim； 4．已知 2235lim2=-++∞→n bn an n ，则 =a ， =b ；5．=-+∞→nnn nn 3535lim；6．已知2003)1(lim=--∞→bban n n n，则 =a ， =b ；7．=+++++++++∞→)12111(lim 222nn n n n n n n ；8． =-∙∙--∞→)11()311)(211(lim 222nn ；二、选择填空1． “对任意给定的)1,0(∈ε，总存在正整数N ，当N n ≥时恒有ε2||≤-a a n ”是数列}{n a 收敛于a 的A 充分条件但非必要条件。

B 必要条件但非充分条件C 充分必要条件D 既非充分条件又非必要条件。

2．数列}{n a 不收敛于a 的充要条件是A 对于任给 0>ε，满足ε<-||a a n 的项只有有限项。

B 对于任给 0>ε，总有相应的项n a ，ε≥-||a a n 。

C 存在某个正数0ε，除有限项外，都有0||ε≥-a a nD 存在某个正数0ε，有无穷多项满足0||ε≥-a a n3． 设数列n x 与n y 满足0lim =∞→n n n y x ，则下列断言正确的是A 若n x 发散，则n y 必发散。

B 若n x 无界，则n y 必有界。

C 若n x 有界，则n y 必为无穷小。

D 若nx 1为无穷小，则n y 必为无穷小。

4． 设}{n a 收敛，}{n b 发散，则A }{n n b a 必收敛。

B }{n n b a 必发散。

C }{n n b a +必收敛。

D }{n n b a +必发散。

5． 设数列}{n a 无上界且 ,2,1,0=≠n a n ，则A }{1-n a 必有上界B 对于任给定的M>0，必有无穷多项M a n >。

（完整word版）数学分析—极限练习题及详细答案⼀、选择题1.若0()lim1sin x x xφ→=，则当x 0→时，函数(x)φ与（）是等价⽆穷⼩。

A.sin ||xB.ln(1)x -C.11.【答案】D 。

2.设f(x)在x=0处存在3阶导数，且0()lim 1tan sin x f x x x→=-则'''f (0)=（）A.5B.3C.1D.0 2.【答案】B.解析由洛必达法得30002()'()''()limlimlim1tan sin 2cos sin sin cos cos x x x f x f x f x x x x x xx x -→→→==-+-42200''()''()lim lim 16cos sin 2cos cos 21x x f x f x x x x x --→→===-++++可得'''f (0)3= 3.当x 0→时，与1x 133-+为同阶⽆穷⼩的是（） A.3x B.34x C.32xD.x3.【答案】A.解析.12233312332000311(1)1133lim lim (1)3313x x x x x x x ---→→→-+?==+=选A 。

4.函数2sin f ()lim 1(2)nn xx x π→∞=+的间断点有（）个A.4B.34.【答案】C.解析.当0.5x >时，分母→∞时()0f x =，故20.5sin 12lim1(2(0.5))2n x π→--=-+?-， 20.5sin12lim1(20.5)2n x π→=+?，故，有两个跳跃间断点，选C 。

5.已知()bx xf x a e=-在（-∞，+∞）内连续，且lim ()0x f x →∞=，则常数a ，b 应满⾜的充要条件是（）A.a>0，b>0B.a ≤0，b>0C.a ≤0，b<0D.a>0，b<05.【答案】B 。