淮安市开明中学初一编班考试数学模拟试题36

图（1） 图（2） 图（3） 图（4） 淮安市开明中学初一编班考试数学模拟试题基础题(立体图形)1. 一个正方体的展开图如右图，那么原来正方体中与B 相对的面是（ ）。

（ D ）A. BB. CC. FD. E2. 在一个正方体表面涂颜色，然后锯成125个小正方体，两面涂色的有（ ）块。

（ C ）A. 8B. 27C. 36D. 243.如果一个正方体的棱长扩大3倍，则它的表面积扩大（ ）。

（ C ）A. 3倍B. 6倍C. 9倍D. 27倍4. 在下面的几个展开图中，哪些可折成正方体（ ）。

（ D ）A.图（1）图（2）图（3）B.图（2）图（3）图（4）C.图（2）图（3）D.图（2图（4））5. 把一个圆柱体钢坯削成一个最大的圆锥体，要削去1.8立方厘米，未削前圆柱的体积是（ ）立方厘米。

（ B ）A. 1.8B. 2.7C. 3.6D.5.46. 如图是一个底面半径3厘米的圆柱木块被削去一半后的形状，它的体积是（ ）立方厘米。

（ C ）A. 30πB. 45πC. 54πD.108π提高题1.把一个棱长6厘米的正方体木块削成一个最大的圆锥，这个圆锥的体积是（）立方厘米。

（ A ）A. 18πB.45πC. 24πD.72π2.一个圆柱的侧面展开后，得到一个边长2π厘米的正方形，圆柱体的表面积是（）平方厘米。

( D )A.4π2B.2π2+ 2πC.4π2+2πD.4π2 +2π3. 如右图，一种礼盒长20厘米，宽8厘米，高5厘米。

把3盒这样的礼盒捆扎在一起（丝带打结处的长度是15厘米），至少需要（）厘米的丝带。

（ D ）A. 116B. 86C. 96D.1314.用一个底面积为94.2平方厘米，高为15厘米的圆锥形容器盛满水，然后把水倒入底面积为31.4平方厘米的圆柱形容器内，水面的高为（）。

（A ）A.1.5分米B.3分米C. 4.5分米D.15分米5.把一根长是2米，底面直径是4分米的圆柱形木料锯成4段后，表面积增加了（）平方分米。

淮安市开明中学初一编班考试数学模拟试题
基础题
1. 结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
2.结果是（B）
A.选项一
B.选项二
C.选项三
D.选项四
3.
结果是（A）
A.选项一
B.选项二
C.选项三
D.选项四
4. 9999×1.26+3333×6.22结果是（B）
A.3333
B.33330
C.1111
D.11110
中等题
1．结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
2. 结果是（C）
A.选项一
B.选项二
C.选项三
D.选项四
3.
其结果是（B）
A.选项一
B.选项二
C.选项三
D.选项四
4．结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
较难题
1.(D)
A.选项一
B.选项二
C.选项三
D.选项四
2.
(B)
A.选项一
B.选项二
C.选项三
D.选项四
3. (A)
A.选
项一
B.选项二
C.选项三
D.选项四
4.观察下列各式：
计算：3×（1×2+2×3+3×4+……+98×99）结果是（B）
A.97×98×99
B.98×99×100
C.99×100×101
D.100×101×102。

淮安市小升初自主招生考试数学模拟测试（一）一、直接写出得数。

（6分）0.48÷0.3＝ 7 8 ÷ 3 4 ＝ 1 3 ×(15＋ 6 7)＝ 6÷( 1 2 － 1 3 )＝ 1－ 2 5 ＋ 3 5 ＝ 3 11 ×9÷ 3 11＝ 二、求X 的值。

（6分）5 6 ＋ 1 6 x ＝2 0.75258x三、下面各题怎样算简便就怎样算。

（9分）6÷ 3 5 － 3 5 ÷6 5 12 × 1 13 － 1 4 ÷13 3 8 ×[ 8 9 ÷( 5 6 － 3 4 )]四、填空。

（48分）1.任何一个三角形至少有_______个锐角2.学校美术组有35人，其中男生人数是女生的23，女生有________人。

3.将一个三角形按2：1的比放大后，面积是原来的_______倍。

4.在一个边长4厘米的正方形中，画一个最大的圆，这个圆的面积是_______平方厘米。

5.把一个圆柱形状的木头削成一个最大的圆锥。

已知削去的体积是24立方厘米，削成的圆锥的体积是（ ）立方厘米。

6.有一个箱子里放着一些黄色乒乓球，为了估计球的数量，我们把20个白色乒乓球放入箱子中，充分搅拌混合后，任意摸出30个球，发现其中3个白球。

你估计箱里原有黄色乒乓球_______个。

7.一个圆柱体的侧面展开图是一个正方形。

这个圆柱的高与圆柱的底面直径比是______。

8.有一种手表零件长5毫米，在设计图纸上的长度是10厘米，图纸的比例尺是_______.9.小明跑1200米的跑程，时间由原来的5分钟缩短到4分钟，速度提高了_______%.10.找规律，填下一个：112＝102＋21，122＝112＋23，132＝122＋25，142＝132＋27，________。

11.一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米，平行四边形的面积是_______平方分米。

淮安市开明中学初一编班考试数学模拟试题
基础题
1. 结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
2.结果是（B）
A.选项一
B.选项二
C.选项三
D.选项四
3.
结果是（A）
A.选项一
B.选项二
C.选项三
D.选项四
4. 9999×1.26+3333×6.22结果是（B）
A.3333
B.33330
C.1111
D.11110
中等题
1．结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
2. 结果是（C）
A.选项一
B.选项二
C.选项三
D.选项四
3.
其结果是（B）
A.选项一
B.选项二
C.选项三
D.选项四
4．结果是（D）
A.选项一
B.选项二
C.选项三
D.选项四
较难题
1.(D)
A.选项一
B.选项二
C.选项三
D.选项四
2.
(B)
A.选项一
B.选项二
C.选项三
D.选项四
3. (A)
A.选
项一
B.选项二
C.选项三
D.选项四
4.观察下列各式：
计算：3×（1×2+2×3+3×4+……+98×99）结果是（B）
A.97×98×99
B.98×99×100
C.99×100×101
D.100×101×102。

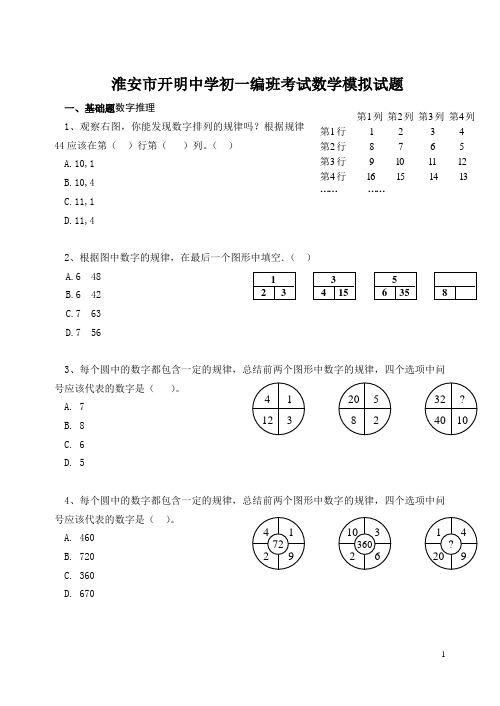
第1列 第2列 第3列 第4列第1行 1 2 3 4 第2行 8 7 6 5 第3行 9 10 11 12 第4行 16 15 14 13 …… ……淮安市开明中学初一编班考试数学模拟试题一、基础题数字推理1、观察右图，你能发现数字排列的规律吗？根据规律44应该在第（ ）行第（ ）列。

（ ） A.10,1 B.10,4 C.11,1 D.11,42、根据图中数字的规律，在最后一个图形中填空．（ ） A.6 48 B.6 42 C.7 63 D.7 563、每个圆中的数字都包含一定的规律，总结前两个图形中数字的规律，四个选项中问号应该代表的数字是（ ）。

A. 7 B. 8 C. 6 D. 54、每个圆中的数字都包含一定的规律，总结前两个图形中数字的规律，四个选项中问号应该代表的数字是（ ）。

A. 460 B. 720 C. 360 D. 6701 2 33 4 155 6 358第1行： 1第二行： 2 3 第三行： 4 5 6 第四行： 7 8 9 10 第五行： … … … … …1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16………………………………中等题1、将1、2、3、4、5、……按一定规律排列如：那么第20行从左至右第10个数是（ ）。

A ．202 B ．201C ．200D ．1992、每个圆中的数字都包含一定的规律，总结前两个图形中数字的规律，四个选项中问号应该代表的数字是（ ）。

A. 1 B. 2 C. 3 D. 43、如图是一个由数字组成的三角形，研究它的规律，第八行最后一位数字是（ ）。

A ．178B ．56C ．64D ．2244、根据右表中数的排列规律，空格里应填上的数是（）。

A.24 B.30 C.42 D.60较难题1、古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如右图。

他们研究图1中1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中1，4，9，16，…，这样的数为正方形数。

江苏省淮安市中考数学模拟试卷一、选择题（本大题共有8小题，每小题0分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．代数式（2a2）3的计算结果是（）A．2a6B．6a5C．8a5D．8a62．﹣2021的绝对值是（）A．2021B．C．﹣D．﹣20213．下列几何体的左视图和俯视图相同的是（）A．B．C．D．4．若点A（1+m，1﹣n）与点B（﹣3，2）关于原点对称，则m+n的值为（）A．﹣1B．2C．3D．55．若有一组数据：1，2，4，8，a，其中整数a是这组数据的中位数，则这组数据的平均数不可能是（）A．3.4B．3.6C．3.8D．46．正五边形的每个内角度数为（）A．36°B．72°C．108°D．120°7．已知⊙O1，⊙O2，⊙O3是等圆，△ABP内接于⊙O1，点C，E分别在⊙O2，⊙O3上．如图，①以C为圆心，AP长为半径作弧交⊙O2于点D，连接CD；②以E为圆心，BP长为半径作弧交⊙O3于点F，连接EF；下面有四个结论：①CD+EF＝AB②③∠CO2D+∠EO3F＝∠AO1B④∠CDO2+∠EFO3＝∠P所有正确结论的序号是（）A．①②③④B．①②③C．②④D．②③④8．如图，两个正方形的边长分别为a，b，如果a+b＝ab＝9，则阴影部分的面积为（）A．9B．18C．27D．36二、填空题（本大题共有8小题，每小题0分，共24分．不需写出解答过程，请把答案直接写在答题卡相应位置上）9．分解因式：﹣2x3+4x2y﹣2xy2＝．10．已知一组数据1，4，a，3，5，若它的平均数是3，则这组数据的中位数是．11．我国对“一带一路”沿线国家不断加大投资，目前已为有关国家创造了近1 100 000 000美元税收，其中1 100 000 000科学记数法表示应为．12．把二次函数y＝x2+3x+的图象向右平移2个单位后，再向上平移3个单位，所得函数图象的顶点是．13．有一个人患了新冠肺炎，经过两轮传染后共有169人患了新冠肺炎，每轮传染中平均一个人传染了个人．14．反比例函数y＝的图象上有一点P（2，n），将点P向右平移1个单位，再向下平移1个单位得到点Q，若点Q也在该函数的图象上，则k＝．15．如图，已知长方形纸片ABCD，点E、F分别在边AD、BC上，将长方形纸片沿直线EF折叠后，点D、C分别落在D1、C1的位置，如果∠AED1＝30°，那么∠EFB的度数为．16．如图，矩形ABCD中，AB＝5，AD＝12，点P在对角线BD上，且BP＝BA，连接AP 并延长，交DC的延长线于点Q，连接BQ，则BQ的长为．三、解答题（本大题共有11小题，共102分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）17．（1）计算：（1﹣）0﹣|﹣2|+（）﹣2；（2）解不等式组：18．先化简，再求值：（﹣）÷，其中x＝．19．2013年5月13日是母亲节，某校预先进行了感恩教育调查．该校从每班随机抽取一部分学生进行调查，并将调查结果绘制成如下的扇形统计图和频数分布直方图．根据上图信息，解答下列问题：（1）求出本次被调查的学生人数，并补全频数分布直方图；（2）若这所学校共有学生2400人，已知被调查的学生中，知道母亲生日的女生人数是男生人数的2倍，请根据上述调查结果估计该校知道母亲生日的女生有多少人？20．一只不透明的袋子中装有2个白球和1个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．（1）用树状图或列表等方法列出所有可能出现的结果；（2）求两次摸到的球的颜色不同的概率．21．如图，在▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F两点，点G，H分别为AD，BC的中点，连接GH交BD于点O．求证：EF与GH互相平分．22．小明和小玲比赛解方程，小玲很细心地算得此方程组的解为，小明抄错了c解得，求a、b、c的值．23．如图是某厂家新开发的一款摩托车，它的大灯射出的光线AB、AC与地面MN的夹角分别为8°和10°，该大灯照亮地面的宽度BC的长为1.4米，求该大灯距地面的高度．（参考数据：sin8°≈，tan8°≈，sin10°≈，tan10°≈）24．如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED＝EA．（1）求证：ED是⊙O的切线；（2）填空：①当OA＝3，AE＝4时，则BC＝．②连接OD，当∠ABC的度数为时，四边形AODE为正方形．25．如图，在平面直角坐标系中，Rt△ABC的斜边BC在直线y＝x上，且O是BC的中点，点A的坐标为（5，0）．点P在线段AC上从C点向A点运动，同时点Q在线段AC 上从A点向C点运动，且PC＝AQ．（1）求BC的长及点B的坐标．（2）作PE⊥AC交BC于点E，作QF⊥BC交BC于点F，连接PF，QE，设PC＝t．①在E，F相遇前，用含t的代数式表示EF的长．②当t为何值时，EQ与坐标轴垂直．（3）若PF交y轴于点D，除点F与点O重合外，的值是否为定值，若是，请直接写出的值，若不是，请直接写出它的取值范围．26．问题提出如图1所示，等边△ABC内接于⊙O，点P是上的任意一点，连接P A，PB，PC．线段P A、PB、PC满足怎样的数量关系？尝试解决为了解决这个问题，小明给出这样种解题思路：发现存在条件CA＝CB，∠ACB＝60°，从而将CP绕点逆时针旋转60°交PB延长线于点M，从而证明△P AC≌△MBC，请你完成余下思考，并直接写出答案：P A、PB、PC的数量关系是；自主探索如图2所示，把原问题中的“等边△ABC”改成“正方形ABCD”，其余条件不变，①PC与P A，PB有怎样的数量关系？请说明理由：②PC+PD与P A，PB的数量关系是．（直接写出结果）灵活应用把原问题中的“等边△ABC”改成“正五边形ABCDE”，其余条件不变，则PC+PD+PE 与P A+PB的数量关系是．（直接写出结果）参考答案一、选择题（本大题共有8小题，每小题0分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．D．2．A．3．D．4．D．5．D．6．C．7．D．8．C．二、填空题（本大题共有8小题，每小题0分，共24分．不需写出解答过程，请把答案直接写在答题卡相应位置上）9．﹣2x（x﹣y）2．10．3．11．1.1×109．12．（﹣1，1）．13．12．14．6．15．75°．16．3．三、解答题（本大题共有11小题，共102分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）17．解：（1）原式＝1﹣2+4＝﹣1+4＝3；（2）解不等式3x﹣2≥1，得：x≥1，解不等式5﹣x＞2，得：x＜3，则不等式组的解集为1≤x＜3．18．解：原式＝[﹣]÷＝•＝，当x＝时，原式＝＝．19．解：（1）被调查学生人数是：30÷＝30÷0.3＝100（人），不知道的人数是：100×＝10（人）知道的人数是：100﹣30﹣10＝60（人）；补图如下：（2）设知道母亲生日的男生有x人，女生有2x人，根据题意得：x+2x＝60，解得：x＝20，女生有2x＝2×20＝40（人），则该校知道母亲生日的女生有：2400×＝960（人），答：该校知道母亲生日的女生有960人．20．解：（1）如图：；（2）共有6种情况，两次摸到的球的颜色不同的情况有4种，概率为＝．21．证明：连接BG、DH，如图所示：∵四边形ABCD为平行四边形，∴AB＝CD，AB∥CD，∴∠ABE＝∠CDF，∵AE⊥BD，CF⊥BD，∴∠AEB＝∠CFD＝90°，在△ABE和△CDF中，．∴△ABE≌△CDF（AAS），∴BE＝DF，∵G，H分别为AD，BC的中点，∴BH＝AB，GD＝AD，且AB＝CD，∴BH＝GD，且BH∥GD，∴四边形BHDG是平行四边形，∴OB＝OD，OG＝OH，∴OB﹣BE＝OD﹣BF，即OE＝OF，∴EF与GH互相平分．22．解：把，代入方程得．小明抄错了c解得，把它代入，得2a﹣6b＝2，与a﹣b＝2组成方程组求解得b＝．把b＝代入a﹣b＝2得a＝．即．23．解：过点A作AD⊥MN于点D，在Rt△ADB与Rt△ACD中，由锐角三角函数的定义可知，＝tan∠ABD，＝①，＝tan∠ACD，＝②，联立两方程得，解得AD＝1．答：该大灯距地面的高度1米．24．（1）证明：如图，连接OD．∵AC⊥AB，∴∠BAC＝90°，即∠OAE＝90°．在△AOE与△DOE中，，∴△AOE≌△DOE（SSS），∴∠OAE＝∠ODE＝90°，即OD⊥ED．又∵OD是⊙O的半径，∴ED是⊙O的切线；（2）①解：如图，在△OAE中，∠OAE＝90°，OA＝3，AE＝4，∴由勾股定理易求OE＝5．∵AB是直径，∴∠ADB＝90°，即AD⊥BC．又∵由（1）知，△AOE≌△DOE，∴∠AEO＝∠DEO，又∵AE＝DE，∴OE⊥AD，∴OE∥BC，∴＝＝，BC＝2OE＝10，即BC的长度是10故答案为：10；②当∠ABC的度数为45°时，四边形AODE为正方形；理由如下：∵OB＝OD，∴∠ODB＝∠ABC＝45°，∴∠BOD＝90°，∴∠AOD＝90°，∵OA＝OD，∴∠OAD＝∠ODA＝45°，∵OA⊥AB于点A，OA是⊙O的半径，∴EA是⊙O的切线，∠EAD＝90°﹣45°＝45°，由（1）知，ED是⊙O的切线，∴EA＝ED，∴∠EDA＝∠EAD＝45°，∴∠ODE＝∠ODA+∠EDA＝45°+45°＝90°，∴∠ODE＝∠AOD＝∠OAE＝90°，∴四边形AODE是矩形，∵OA＝OD，∴矩形AODE为正方形，故答案为：45°．25．解：（1）如图1，过点B作BG⊥x轴于点G．∵OB＝OC，∠BAC＝90°，A（5，0），∴AO＝BC＝5，∴BC＝10；设B（3a，4a），则（3a）2+（4a）2＝52，解得a＝1，∴B（3，4）．（2）①如图1，∵AG＝5﹣3＝2，BG＝4，∴AB＝＝2，∵△ABC∽△AGB，∴AB：AC：BC＝1：2：，∴AC＝4，∴CE＝PC＝t，CF＝CQ＝（4﹣t）＝8﹣t，∴EF＝8﹣t﹣t＝8﹣t．②当EQ⊥y轴时，如图2，则∠CQE＝∠CAO＝∠C，∴QE＝CE，∴EF＝QE＝CE，∴8﹣t＝×t，解得t＝；当EQ⊥x轴时，如图3，则∠EQF＝∠AOB，∴QF＝EF，∵QF＝（4﹣t）＝4﹣t，EF＝t﹣（4﹣t）＝t﹣8，∴4﹣t＝（t﹣8），解得t＝．综上所述，当t＝或t＝时，EQ与坐标轴垂直．（3）分别过点P、F作y轴的垂线，垂足分别为H、L．当点P在y轴左侧时，如图4，设AC交y轴于点K，LF＝OF＝[（4﹣t）﹣5]＝（3﹣2t），PH＝PK＝（4﹣﹣t）＝（3﹣2t），∴＝＝；当点P在y轴右侧时，如图5，LF＝OF＝[5﹣（4﹣t）]＝（2t﹣3），PH＝PK＝[t﹣（4﹣）]＝（2t﹣3），∴＝＝．综上所述，＝．故答案为：是，．26．解：（1）∵△ABC是等边三角形，∴CA＝CB，且∠ACB＝60°，将CP绕点逆时针旋转60°交PB延长线于点M，如图1，∴∠PCM＝∠ACB＝60°，∴∠PCM﹣∠PCB＝∠ACB﹣∠PCB，∴∠ACP＝∠BCM，∵四边形ACMP为圆内接四边形，∴∠CAP+∠CBP＝180°，又∠CBP+∠CBM＝180°，∴∠CAP＝∠CBM，在△ACP与△BCM中，，∴△CAP≌△CBM（ASA），∴CP＝CM，AP＝BM，又∠PCM＝60°，∴△CPM为等边三角形，∴PM＝PC，∵PM＝PB+BM，∴PC＝P A+PB，故答案为：PC＝P A+PB；（2）①，理由如下：如图2，连接AC，将BP绕B顺时针转90°交PC于M点，则∠PBM＝90°，∵四边形ABCD为正方形，∴BA＝BC，∠ABC＝90°，∠CAB＝45°，∴∠ABC＝∠PBM＝90°，∴∠ABP＝∠CBM，在△ABP与△CBM中，∴△ABP≌△CBM（ASA），∴AP＝CM，∵∠CPB＝∠CAB＝45°，∴∠CPB＝∠BMP＝45°，∴△BMP为等腰直角三角形，∴PM＝，∵PC＝PM+CM，∴PC＝P A+；②如图3，连接BD，将P A绕A点逆时针转90°交DP于N，则∠P AN＝∠DAB＝90°，∴∠DAN＝BAP，在△ADN与△ABP中，，∴△ADN≌△ABP（ASA），∴DN＝PB，∵∠DP A＝∠DBA＝45°，又∠NAP＝90°，∴△NAP为等腰直角三角形，∴P A＝NA，∴PN＝，∵PD＝PN+DN，∴PD＝，又由①可得，PC＝P A+，∴，故答案为：；（3）如图4，在PC上截取CF，使CF＝P A，∵四边形ABCDE为正五边形，∴BA＝BC，∠ABC＝∠BCD＝108°，在△BCF与△BAP中，，∴△BCF≌△BAP（SAS），∴BF＝BP，∠CBF＝∠ABP，∴∠PBF＝∠ABC＝108°，∴△PBF为顶角是108°的等腰三角形，延长PD至M，使DM＝PB，连接CM，∵四边形DPBC为圆内接四边形，∴∠PDC+∠PBC＝180°，∵∠PDC+∠MDC＝180°，∴∠PBC＝∠MDC，又PB＝MD，BC＝DC，∴△PBC≌△MDC（SAS），∴∠MCD＝∠PCB，PC＝MC，∴∠PCM＝∠BCD＝108°，∴△PCM为顶角108°的等腰三角形，在PM上取一点Q，使QM＝QC，∴∠M＝∠MCQ＝36°，∴∠MCQ＝∠MPC＝36°，又∠M＝∠M，∴△MCQ∽△MPC，∴MC2＝MQ•MP，设MQ＝x，MC＝CP＝y，∵∠PQC＝2∠M＝72°，∴∠QCP＝∠PQC＝72°，∴PQ＝CP＝y，∴y2＝x（x+y），∴，∴①同理，PF＝②，PD+P A＝③，设P A＝m，PB＝n，由①得，PD+n＝，由②得，PC﹣m＝n，∴，∴，由③得，PE＝，∴PC+PD+PE＝，故答案为：PC+PD+PE＝．。

淮安市开明中学初一编班考试数学模拟试题一、基础题（行程问题）1.一架飞机在甲、乙两城之间飞行，无风时每小时飞552千米，在一次往返飞行中，飞机顺风飞行了5．5小时，逆风飞行了6小时，问风速是每小时多少千米？（B ）A.12KM/hB.24 KM/hC.36 KM/hD.48 KM/h2.甲乙两地相距180千米，一辆汽车从甲地开往乙地，行了全程的53，此时这辆汽车距离甲地多少千米？(C)A.36KMB.72KMC.108KMD.144KM3.一列火车2小时行驶了187千米。

照这样计算，这列火车4.5小时可行驶多少千米？(D)A.396.75KMB.402.75KMC.418.75KMD.420.75KM4.甲乙两人分别从A 、B 两地同时相向而行，甲每分钟行100米，乙每分钟行120米，12.5分钟后两人相距150米。

A 、B 两地相距多少米？(A)A.2900KMB.3600KMC.4200KMD.4800KM5.快车和慢车同时从甲城驶向乙城，速度比是5:3，快车到达乙城后立即以原速返回甲城，在离乙城20千米处和慢车相遇。

甲、乙两城相距多少千米？(C)A.40KMB.60KMC.80KMD.100KM提高题1.一辆快客上午8：00从甲地开往乙地，到下午2：00正好走完了全程的40%，这时汽车离全程的一半还差42千米。

问这辆汽车平均每小时行驶多少千米？(C)A.12KM/hB.26 KM/hC.28 KM/hD.32 KM/h2.甲乙两辆汽车同时从两地相向而行，甲车每小时行45千米，乙车每小时行42千米。

两车在距离中点12千米处相遇。

两车同时开出后经过多少小时相遇？ (C)A.4小时B.6小时C.8小时D.10小时3.甲乙两车同时从AB 两地相向而行，5小时相遇，相遇后继续前进，又经过4小时，甲车到达B 地，乙车离A 地还有80千米。

求AB 相距多少千米？(B)A.200KMB.400KMC.600KMD.800KM4.AB 两地相距270千米，甲、乙两车同时从A 地出发去B 地，甲车的速度是乙车的2倍，当甲车到达B 地后立即沿原路返回，乙车在出发3小时后与甲车相遇，求乙车的速度。

淮安市初一新生编班考试数学模拟试题（五）一、 选择。

下面各题给出的答案中，正确的不一定只有一个，请把正确答案的编号字母写在横线上 1. 下面的比中，能：52 74与组成比例的是A. 2:4B.7:5C.7:10D.10:7E.21： 75 2. 一个真分数，把它的分子和分母同时加上同一个不为零的数，所得到的新分数与原分数比较大小是：A.原分数大；B.原分数小C. 大小不变D.大小没法确定 3. 下面五个数中，最接近1的是A .78 B. 98 C. 56 D. 1011 E.3129 4. a 是质数，b 是合数。

下面的式子中，值一定是合数的为：A.b a +3;B. ab ;C. a ab ÷;D.b a ÷ b215. 已知：△+△+△=☆，☆+☆+☆=□+□，那么△：□是：A.2:9B.1:6;C.9:2;D.3:2;E.1:3 6. 规定：b a b a 23-=∆。

已知7)14(=∆∆x ，那么=∆5x A.7; B.17; C.9; D.19; E.36二、 计算下列各题，能巧算的要用简便方法计算，并写出主要的计算过程1. 4324154107÷⎪⎭⎫ ⎝⎛-+ 2. 7115216953⨯⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--3. ._________________420120121361221=++++Λ4. 4. 2519235.7⨯+⨯5.400300200864432300200100642321⨯⨯++⨯⨯+⨯⨯⨯⨯++⨯⨯+⨯⨯ΛΛ三、 填空1．两个质数的倒数相加的和的分子是31，和的分母是（ ）2．某地去年十二份得一天，最高温度是C o12(摄氏度)，最低温度是C o4-，这一天最低与最高温度相差（ ）C o3．右图平行四边形ABCD 中，AD=10cm ，直角三角形BCE 中，EC= 10 cm 。

图中阴影部分面积比三角形EFG 的面积大82cm ，EG 长（ ）厘米。

淮安市开明中学初一编班考试数学模拟试题定义新运算低等难度：1.新定义运算：对任意正整数a、b规定a*b=2a+3b-9，请计算8*12=（）BA 39B 43C 52D 482. 6◇2=6+66=72，2◇3=2+22+222=246，1◇4=1+11+111+1111=1234，7◇5=（）CA 6172835B 8638C 86415D 863153.在有理数范围内定义新运算“*”，其规则为a*b=a/2-b,则方程2x*x/4=1的解为（）DA 1B 4C 3/4D 4/3中等难度：1.两个整数a和b，a除以b的余数记为a①b。

例如：9①4＝1，根据这样的定义新运算﹙47①8﹚①5＝（）CA 1B 5C 7D 22.如果a○b表示（3a-2b），例如：4○5=3×4-2×5=2，那么当x○5比5○x大5时， x=（）CA 30B 0C 6D 203.对于两个数a、b，规定a△b=ax-2b。

已知58△75=24，95△84=( )AA 117B 22C 179D 3高等难度：1.规定正整数n的“H运算”是：1、当n为奇数时，H=3n+13；2、当n为偶数时，H=n*0.5*0.5……（其中H为奇数，即运算结果得到奇数为止）。

如：数5经过1次H运算的结果是28，经过2次H运算的结果是7，经过3次H运算是34.那么数257经过257次H运算的结果是...( )DA 49B 64C 1D 162.a*b=a+（a+1)+(a+2)+(a+3）+…+（a+b-1),那麼x*10=65中x的值是( )BA 2B 1/2C 3D 1/3。

淮安市名校初一新生分班考试数学测试卷有答案（时间：100分钟总分：100分）一、填空题。

(第15、17题每题1分，其余每空1分，共30分）1. 九千八百零五万零四十写作（），“四舍五人”到亿位，且保留一位小数是（）亿。

2. 在算盘上拨一个四位数，用了11个珠子，这个数最大是（ ),最小是（）。

3. 从6、0、1、2四张卡片中选择三张组成是3的倍数的三位数，共可以组成（ ) 个。

4. 用1、6、3和4算出24点，列式是（）5. 已知m: 4. 5=n: 3, 且2m+6n=7. 2, 那么m= ( ) ,n= ( ) .6. 李大爷活了72周岁，他每天平均睡觉8小时，他这一生共睡觉（）年。

7. 从24的因数中选择4个合数组成比例是（）8. 有9、27、81和243四个数，每次从中取一个数，或两个数，或几个不同的数求和，这些和从小到大排列，那么第13个数是（） .9. 从A地到B地，去与回的速度比是7: 9. 去时用了6. 3小时，回来用了（）小时。

10. 右图是一个水龙头打开后的出水量统计图。

(1) 这个水龙头打开的时间与出水量成（）比例。

（2) 如果出水量达到480升，需要（）分钟。

（3) 如果打开水龙头1小时，出水量达到（ ) 立方米。

时间/秒11. 烟花三月是旅游的旺季，宾馆床位比较紧张。

一个旅游团有47名男游客、46名女游客到宾馆住宿，宾馆恰好有11人间、7人间和4人间客房。

男、女分开住，每间客房都住满，至少需要（ ) 间房。

12. 3时（）分，钟面上时针与分针的最小夹角是102.5°.13. 六年级学生排成一个正方形方队，最外面两层的学生穿红衣服，其他的学生穿黄衣服，已知穿红衣服的学生有56人，穿黄衣服的学生有（）人。

14. 有长为整厘米数的两根小棒a、b, 再用一根长为整厘米数的小棒c可以围成一个三角形，c最长是m厘米，最短是n厘米，已知m与n的和是18厘米，差是6厘米。

如果用a、b与c围成一个等腰三角形，那么这个等腰三角形的周长最小是（）厘米。