成都七中高2012级高一(下)周末练习——不等式的性质

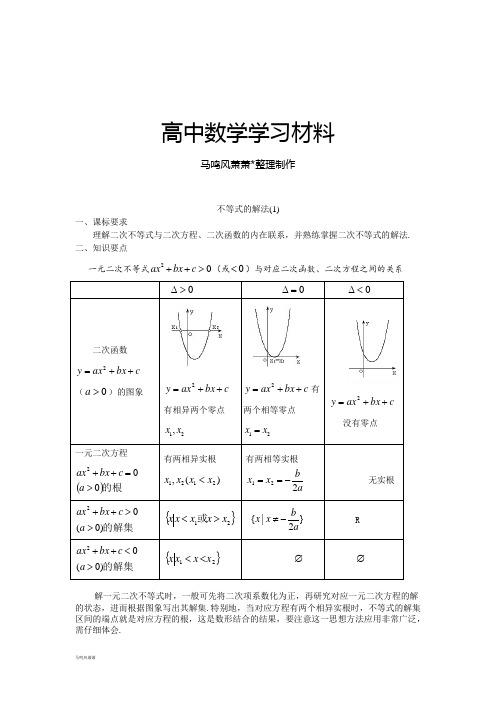
高中数学学习材料马鸣风萧萧*整理制作不等式的解法(1)一、课标要求理解二次不等式与二次方程、二次函数的内在联系，并熟练掌握二次不等式的解法. 二、知识要点一元二次不等式20ax bx c ++>（或0<）与对应二次函数、二次方程之间的关系0>∆0=∆0<∆二次函数c bx ax y ++=2（0>a ）的图象c bx ax y ++=2有相异两个零点12,x xc bx ax y ++=2有两个相等零点12x x =c bx ax y ++=2没有零点一元二次方程()的根002>=++a c bx ax有两相异实根 )(,2121x x x x < 有两相等实根ab x x 221-==无实根的解集)0(02>>++a c bx ax{}21x x x x x ><或{|}2b x x a≠-R的解集)0(02><++a c bx ax{}21x x xx <<∅ ∅解一元二次不等式时，一般可先将二次项系数化为正，再研究对应一元二次方程的解的状态，进而根据图象写出其解集.特别地，当对应方程有两个相异实根时，不等式的解集区间的端点就是对应方程的根，这是数形结合的结果，要注意这一思想方法应用非常广泛，需仔细体会.三、典型例题例1.求下列不等式的解集（1）x x x 3)2(≤-；（2）22320x x -++>；（3）220x x -+> 【解析】（1）不等式可化为220x x +-≥，方程有两个实数根122,1x x =-=，而22y x x =+-的图象是开口向上的抛物线， 所以，原不等式的解集为{}12x x x ≥≤-或.（2）不等式可化为22320x x --<，方程有两个实数根121,22x x =-=， 而2232y x x =--的图象是开口向上的抛物线， 所以，原不等式的解集为122x x ⎧⎫-<<⎨⎬⎩⎭（3）因为2(1)4270∆=--⨯=-<，所以方程220x x -+=无实数根， 又因为22y x x =-+的图象是开口向上的抛物线，所以，原不等式的解集为R ． 变式1. 求下列不等式的解集.（1）2340x x +->； （2）2340x x -+-≥.【解析】（1）方程2340x x +-=两根为4,1-，该不等式解集“两根之外”，即原不等式的解集为{}14x x x ><-或.（2）原不等式可化为2340x x -+≤，因为2(3)4470∆=--⨯=-<，所以方程2340x x -+=无实数根，又因为22y x x =-+的图象是开口向上的抛物线，所以，原不等式的解集为Φ．例2. （1）解不等式组：x x x x 223401271502--≥--<⎧⎨⎪⎩⎪()()；（2）解不等式（）x x x ---≥22302. 【解析】(1)由解（1）得x x ≤-≥14或,解（2）得-<<325x∴-<≤-≤<原不等式组的解集为或{|}x x x 32145 （2）原不等式可化为x x x 223020-->-≥⎧⎨⎩或x x x R 22302--=-∈⎧⎨⎩解x x x 223020-->-≥⎧⎨⎩得x x <->13或；解x x x R22302--=-∈⎧⎨⎩得x x =-=13或. 综上，所求不等式的解集为{}x x x |≤-≥13或.变式2.解不等式组x x x a a R 2222300--≥-≤⎧⎨⎪⎩⎪∈+(). 【解析】由题意：x x a x a≥≤--<<⎧⎨⎩31或，故：当01a <≤时，不等式的解集为x ∈Φ；当13a <≤时，不等式的解集为{|1}x a x -<≤-； 当3a >时，不等式的解集为{|13}x a x x a -<≤-≤<或.例3.已知不等式20ax bx c ++>的解集为{}2,1x x x ><-或，求不等式20cx bx a ++>的解集.【解】由题意可得0a >，且1,2-为方程20ax bx c ++=的两个根． 由根与系数的关系（韦达定理）可得，12(1)2b ac a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，解之2b a c a =-⎧⎨=-⎩ （*） 将（*）代入所求不等式20cx bx a ++<，得220ax ax a --+>， 又因为0a >，所以化简为2210x x +-<，解得112x -<<. 因此不等式20cx bx a ++<的解集为112x x ⎧⎫-<<⎨⎬⎩⎭. 变式3.已知函数2()f x ax bx c =++，当(1,2)x ∈-时()0f x >，当(,1)(2,)x ∈-∞-+∞时()0f x <，求不等式20cx bx a ++>的解集.【解析】据题意知0a <，121,2x x =-=是方程20ax bx c ++=的两根.由韦达定理知：122012b b a acc a a ⎧-+=-⎪=-⎧⎪⇒⎨⎨=->⎩⎪-⋅=⎪⎩故不等式20cx bx a ++>为：220ax ax a --+>.由0a <得：2210x x +->，解得112x x <->或.∴不等式20cx bx a ++>的解集为1{|1}2x x x <->或.四、备选例题例1. 设函数，则不等式的解集是（ ）A. B. C. D. 【解析】∵10>，∴(1)1463f =-+=，根据分段函数的意义，不等式()(1)f x f >等价于2463x x x ≥⎧⎨-+>⎩ ①或063x x <⎧⎨+>⎩ ②.其中：①20001313430x x x x x x x x ≥≥⎧⎧⇔⇔⇔≤<>⎨⎨<>-+>⎩⎩或或， ②0303x x x <⎧⇔-<<⎨>-⎩，综上知313x x -<<>或，选A.例2. 二次函数f (x )2(2)a x k =-+(0)a >定义域为]3,1[-，若f (1－2x 2)＜f (1+2x －x 2)，则x 的取值范围是（ ） （A ）.x ＞（B ）x ＜－2或0＜x ＜（C ）－2＜x ＜0 （D ）01<≤-x【解析】由题意： f (x )的图象开口向上，对称轴为2=x ，所以)(x f 在[1,2]-上单调递减，注意2)1(221,2121222≤--=-+=<≤-=x x x s x t ，故：f (1－2x 2)＜f (1+2x －x 2)012121321132112222<≤-⇒⎪⎩⎪⎨⎧-+>-≤-+≤-≤-≤-⇔x x x x x x x ，故选D.五、小结与反思六、练习1．不等式28210x x -++≥的解集是（ ）A.11[,]42-B. 11[,]24-C. 11[,]42D. 11[,]24--⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f )1()(f x f >),3()1,3(+∞⋃-),2()1,3(+∞⋃-),3()1,1(+∞⋃-)3,1()3,(⋃--∞【答案】A2．在下列不等式中，解集是∅的是（ ）.A ．0442<+-x xB ．22320x x -+->C ．22320x x -+>D ．2210x x ++≤ 【答案】A3．若关于x 的不等式20x x c +->的解集是全体实数，那么（ ）.A ．14c <-B ．14c ≤-C ．14c >-D ．14c ≥-【答案】A4．若二次函数f (x ) = ax 2 + bx + c （a ≠0）的部分对应值如下表所示： 则不等式f (x )＜0的解集为（ ）． A ．（－2，3） B ．（－∞，－2）∪（3，+∞） C ．（－2，1） D ．（1，3）【解析】由函数值表易知，两根分别是x 1 =－2和x 2 = 3，而两根之间的函数值比0小，故选A ．5．1212()()()(0,)f x a x x x x a x x =--<<，若()1f m >，则m 与12,x x 的大小关系（ ）． A ．1m x < B ．2m x > C ．12x m x << D ．无法确定 【解析】选C. 6．不等式(1)(2)03x x x --≥-的解集为（ ）． A. (,1][2,3]-∞ B. [1,2][3,+)∞ C. (,1][2,3)-∞ D. [1,2](3,+)∞【解析】选D.7. 若关于x 的不等式(1)2)0mx x -->（的解集为1{|2}x x m<<，则m 的取值范围是 . 【解析】由不等式的解集形式知12m<且0m <，故m ＜0. 8.不等式：0242<--<x x 的解集为 .【解析】22220120242324x x x x x x x x x ⎧--><->⎧⎪<--<⇔⇔⎨⎨-<<--<⎪⎩⎩或， 故原不等式的解集为：{}x x x -<<-<<2123或 9.给出下列命题：不等式302x x-≥-与(3)(2)0x x --≥同解；②不等式x a a a 2<-的解集为(,)；③不等式33122x x x +>+--的解集为{}|1x x >；④不等式(2)x x x ->的解集是{|2}x x >；⑤不等式22(2)x x x -≥的解集是{|2}x x ≥；⑥不等式22(2)x x x ->的解集是{|2}x x >.x －2 1 3 f (x ) 0 －6 0其中正确命题的序号是 .【解析】①中两个不等式不同解，原因在于2x =符合(3)(2)0x x --≥但不符合302x x-≥-；②中当0a ≤时x ∈Φ，故不成立；对于③，在解x x x +->+-32132时要注意等价转化，考虑函数的定义域，将解不等式问题转化为解不等式组解决：x x x x >-≠⎧⎨⎩⇔>≠12012,且； ④忽略了x 的符号；⑤中忽略了0x =；⑥显然正确.10．求下列不等式的解集（1）2340x x -->；（2）4 ； （3）【解析】（1）方程的2340(1)(4)0x x x x --=⇔+-=，两根为1,4-， 故2340x x --=的解集为{|1x x <-或4}x >.（2）42(21)0x ⇔->，故其解集为1{|}2x x R x ∈≠且. （3）原不等式为：2230x x -+<，4120∆=-<，故其解集为空集Φ.11.已知函数2()1f x ax bx =++，方程()0f x =的两根个分别为11,3-. (1)求()f x 的解析式;(2)求不等式(()4)0x f x +>的解集. 【解析】(1)由题意，210ax bx ++=的两个根分别为11,3-， 由韦达定理得：11311(1)3b a a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，解之32a b =-⎧⎨=-⎩，∴2()321f x x x =--+.(2)由（1）知，0)53)(1(0523052304)(22<+-⇔<-+⇔>+--⇔>+x x x x x x x f ，解得513x -<<，考虑到0x >，有01x <<；()40f x +<⇔513x x <->或，结合0x <，有53x <-，综上，不等式(()4)0x f x +>的解集为5{|01}3x x x <-<<或.12．已知二次函数f （x ）的二次项系数为a ，且不等式f （x ）＞－2x 的解集为（1，3）． （1）若方程f （x ）+ 6a = 0有两个相等的根，求f （x ）的解析式； （2）若f （x ）的最大值为正数，求a 的取值范围． 【解析】（1）因为不等式 f （x ）+ 2x ＞0的解集为（1，3），知a ＜0，设 f （x ）+ 2x = a （x －1）（x －3）， 则f （x ）= a （x －1）（x －3）－2x = ax 2－（2 + 4a ）x + 3a ． ① 由方程 f （x ）+ 6a = 0 得 ax 2－（2 + 4a ）x + 9a = 0． ②因为方程②有两个相等的根，0142>+-x x 0322>-+-x x 0142>+-x x所以 △= [－（2 + 4a ）]2－4a ×9a = 0， 即 5a 2－4a －1 = 0，解得a = 1 或 51-=a ． 由于a ＜0，取51-=a ，即51-=a . 代入①得 f （x ）的解析式为535651)(2---=x x x f ．（2）由f （x ）= ax 2－2（1 + 2a ）x + 3a= aa a a a x a 14)21(22++-+-及a ＜0， 可得 f （x ）的最大值为aa a 142++-．由 ⎪⎩⎪⎨⎧<>++-0,0142a a a a 解得 32--<a 或032<<+-a ．故当 f （x ）的最大值为正数时，实数a 的取值范围是)0,32()32,(+-⋃---∞．。

不等式的性质1. 若b a c b a >∈,R 、、，则下列不等式成立的是( )A.ba 11<. B.22b a >. C .1122+>+cb ca . D.||||cbc a >.2. 已知a 、b 、c 满足c b a <<，且ac <0，那么下列选项中不一定成立的是（ ）A ．ab ac >B ．c b a ()-<0C .cb ab 22< D ． 0)(<-c a ac 3. 对于实数，下命题正确的是 ( )A.若a<b,则ba 11>. B.若b a <,则ba ab >.C .若0<<b a ,则22b ab a >>. D.若a>b>0,d>c>0,则a b cd<4. 已知三个不等式：ab ＞0，bc －ad ＞0，ac－bd ＞0（其中a 、b 、c 、d 均为实数），用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是 A.0B.1C.2 D .35. 对于10<<a ，给出下列四个不等式①)11(log )1(log aa a a +<+②)11(log )1(log aa a a +>+③a aa a 111++<④aaaa111++>其中成立的是_________6. “0>>b a ”是“222ab a b <+”的 ( )A .充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不允分也不必要条件 7. 若0,0a b >>,则不等式1b a x-<<等价于（ ）A.1100x x ba-或<<<< B. 11x ab-<< C. 11x x a b -或<> D . 11x x ba-或<>8. (2004湖北)若011<<ba ，则下列不等式①ab b a <+；②|;|||b a >③b a <；④2>+ba ab 中，正确的不等式有 （ ）A ．1个B ．2个C ．3个D ．4个9. 已知a ＞2，b ＞2，则a +b 与ab 的大小关系是___∵ab －（a +b ）=（a －1）（b－1）－1＞0.∴ab ＞a +b ._______.10. 已知－1＜2a ＜0，A =1+a 2，B =1－a 2，C =a+11，D =a-11则A 、B 、C 、D 按从小到大的顺序排列起来是___ D ＜B ＜A ＜C ._____.11. a ＞b ＞0，m ＞0，n ＞0，则a b ，ba ，ma mb ++，nb n a ++的由大到小的顺序是____ba ＞nb n a ++＞ma mb ++＞ab _. 12. 如果R b a ∈,，求不等式ba b a 11,>>同时成立的条件．解：00011<⇒⎪⎭⎪⎬⎫<-⇒>>-=-ab a b b a abab b a 13. 已知Rc b a ∈,,，0,0<=++abc c b a 求证：0111>++cba证：∵0=++c b a ∴222c b a ++0222=+++bc ac ab 又∵0≠abc ∴222c b a ++>0 ∴0<++bc ac ab∵abccabc ab c b a ++=++111 0<abc 且0<++bc ac ab∴0111>++cba14. 已知||||,0b a ab >> 比较a1与b1的大小．解：a1-b1aba b -=当0,0>>b a 时∵||||b a >即b a >0<-a b 0>ab ∴0<-aba b ∴a1<b1当0,0<<b a 时∵||||b a >即b a <0>-a b 0>ab ∴0>-aba b ∴a1>b115. 设f(x)=ax 2+bx,且1≤f(－1) ≤2, 2≤f(1) ≤4 ,求f(－2)的取值范围解：由已知1≤a －b ≤2, ①, 2≤a+b ≤4 ② 若将f(－2)=4a －2b 用a －b 与a+b,表示，则问题得解设4a －2b=m(a －b)+n(a+b), (m,n 为待定系数) 即4a －2b=（m+n ）a －(m －n)b,于是得{42=+=-n m n m 得：m=3, n=1 由①×3+②×1得5≤4a-2b ≤10即5≤f(－2)≤10, 另法：由{(1)(1)a b f a b f -=-+=得1[(1)(1)]21[(1)(1)]2a f fb f f =+-=--⎧⎨⎩ ∴f(－2)=4a －2b=3 f(－1)+f(1)……16. 已知函数f(x)=ax2-c 满足-4<＝f(1)<=－1，-1<=f(2)<=5,求f(3)的取值范围。

3.1.2 不等式的性质一、解答题。

1. 判断下列各说法的正确性，并说明理由．若ac2>bc2，则a>b，反之也成立．若a>b，则1a <1b.若a<b，c<0，则ca <cb．若a>b，c>a，则a−c>b−d．若a>b>0，a>c，则a2>bc．若a>b，m∈N+，则a m>b m．2. 设a，b是非零实数，若a<b，则下列不等式成立的是（）A.a2<b2B.ab2<a2bC.1ab2<1a2bD.ba<ab3. 若a>b>0，则下列不等式中恒成立的是（）A.b a >b+1a+1B.a+1a>b+1bC.a+1b>b+1aD.2a+ba+2b>ab4. 对于任意实数a，b，c，d，以下四个命题：①若a>b，c>d，则a+c>b+d；②若ac2>bc2，则a>b；③若a>b，则1a <1b；④若a>b，c>d，则ac>bd，其中正确的个数是（）A.1B.2C.3D.45. 如果a，b，c满足c<b<a且ac<0，那么下列选项中不一定成立的是（）A.b a >caB.c(b−a)>0C.cb2<ab2D.ac(a−c)<06. 设a>b>1，c<0，给出下列三个结论：①ca >cb；②a c<b c；③log b(a−c)>log a(b−c)．其中所有正确结论的序号是（）A.①B.①②C.②③D.①②③7. 如果30<x<42，16<y<24，分别求x+y，x−2y及xy的取值范围．8. 若α，β满足−π2<α<0<β<π3，则α−β的取值范围是（）A.(−π2,−π3) B.(−5π6,0) C.(−π2,π3) D.(−π6,0)9. 已知1<a<3，2<b<6，则2a+b的范围是________；a−2b的范围是________；ab的范围是________；ba的范围是________．10. 已知−1<a+b<3且2<a−b<4，求2a+3b的取值范围．11. 设f(x)=ax2+bx，1≤f(−1)≤2，2≤f(1)≤4，求f(−2)的取值范围．12. 解答下列小题：如果a>b，能否得出1a <1b？证明：如果a>b，ab>0，那么1a <1b；如果a>b，ab<0，那么1a>1b．13. 已知下列三个不等式：①ab>0；②ca >db；③bc>ad，以其中两个作为条件，余下一个作结论，则可组成________个正确命题．14. 若1a <1b<0，则下列不等式：①a+b<ab；②|a|>|b|；③a<b；④a2<b2中，正确的不等式有（）A.1个B.2个C.3个D.4个15. 若c>x>y>0．证明：xc−x >yc−y．参考答案与试题解析 3.1.2 不等式的性质一、解答题。

书山有路勤为径；学海无涯苦作舟
高一数学不等式的性质检测考试卷（有答案）
3.1.2不等式的性质第二课时优化练习
1．若0;a>;0，m>;0，则ab;a1>;0，b2>;a2>;0，且a1b1;N
B．M;0，b>;0,0;bb＋1＋aa＋1＝N，
故选A.
6.如图，体积为V的大球内有4个小球，每个小球的球面过大球球心且与大球球面有且只有一个交点，4个小球的球心是以大球球心为中心的正
方形的4个顶点，设V1为小球相交部分(图中阴影部分)的体积，V2为大
球内、小球外的部分(图中玄色部分)的体积，则下列关系式中正确的是()
A．V1>;V2 B．V2;V2 D．V1;0，所以V2>;V1，故选D.
7．(2010年高考辽宁卷)已知－1＜x＋y＜4且2＜x－y＜3，则
z＝2x－3y的取值范围是________．
解析：设z＝2x－3y＝m(x＋y)＋n(x－y)，
则m＋n＝2m－n＝－3，解得m＝－12n＝52.
又∵－2＜－12(x＋y)＜12，
5＜52(x－y)＜152，
∴3＜2x－3y＜8.
答案：(3,8)
8．已知a>;b>;c，且a＋b＋c＝0，则b2－4ac的值的符号为______．
解析：a＋b＋c＝0，∴b＝－(a＋c)，
b2＝a2＋c2＋2ac≥4ac.∵a≠c，∴b2－4ac>;0.
专注下一代成长，为了孩子。

高一数学不等式的性质试题答案及解析1.设，则下列不等式成立的是（）A．B．C．D．【答案】C【解析】由于，；又，因此，所以.【考点】不等式的应用.2.,,则与的大小关系为．【答案】【解析】作差法比较大小，，,,所以p-q,【考点】利用不等式比较大小3.设，且，则（）A．B．C．D．【答案】C.【解析】A：由及不等式的性质可知仅当时，成立，∴A错误；B：，而的符号未定，因此无法判断两者大小关系，∴B错误；C：根据，可知在上递增，因此由可得，∴C正确；D：，而的符号未定，因此无法判定两者大小关系，∴D错误.【考点】1.作差法比较代数式的大小；2.函数结合不等式.4.当时，关于的不等式的解集是（）A．B．C．D．【答案】A.【解析】，∵，∴，，∴不等式的解集为.【考点】解不等式.5.若,则下列不等式成立的是（）A．B．C．D．【答案】D【解析】因为，而函数再R上是减函数，所以，故答案选D.【考点】比较大小；指数函数的性质.6.已知不等式的解集是．（1）若，求的取值范围；（2）若，求不等式的解集．【答案】（1）（2）【解析】（1）由，说明元素2满足不等式，代入即可求出的取值范围；（2）由，是方程的两个根，由韦达定理即可求出，代入原不等式解一元二次不等式即可；（1）∵，∴，∴（2）∵，∴是方程的两个根，∴由韦达定理得解得∴不等式即为：其解集为．【考点】一元二次不等式的解法7.下列命题正确的是（）A．B．C．当且时，D．【答案】D【解析】A:当c<0时，错误；B：，∴；C:当即时不成立；D：正确．【考点】不等式的性质．8.已知，把按从小到大的顺序用“”连接起来： .【答案】【解析】多个数比较大小，一般先进行分类.因为，所以最小，只需比较大小即可. 是两种不同形式，一个是对数值，另一个是三角函数值，比较它们大小需借助第三量进行传递，第三量选择为数1，即【考点】比较大小.9.设a，b为正实数，下列结论正确的是①若a－b=1，则a－b<1；②若，则a－b<1；③若，则|a－b|<1；④若|a－b|=1，则|a－b|<1.A．①②B．②④C．①③D．①④【答案】D【解析】因为，a－b=1，a，b为正实数，所以，，而>0，故，，a－b<1，①正确；排除B。

高一数学同步测试——不等式的性质一、课堂目标：理解不等式的性质定理及其证明。

不等式的性质的简单应用。

二、要点回顾：1. 两个实数比较大小的作差法的依据是：.0,0,0⇔<-⇔=-⇔>-b a b a b a2. 不等式的基本性质： ①对称性： ；②传递性： ；③加法单调性： ；同向不等式可加性： ；④乘法单调性：若0,>>c b a 则 ；若0,<>c b a 则 。

⑤同向正值不等式可乘性： ；⑥正值不等式可乘方： ； ⑦正值不等式可开方： ： ⑧倒数法则： 。

3. 判断下列各命题的真假：①如果b a >，那么c b c a ->-： ；②如果b a >，那么c b c a >： ； ③如果bc ac <，那么b a <： ；④如果22bc ac >，那么b a >： 。

⑤如果b a >，那么22b a >： ；⑥如果0,0>>>>d c b a ，那么db c a >： ⑦如果b a >，那么b a 11>： ；⑧如果b ax >，那么ab x >： 。

三、目标训练 1．设dc b a >>,，下列不等式成立是 （ ）A. d b c a ->-B.bd ac >C. c a d b +<+D. bc ac >2．下列命题成立是 （ ）A. 如果b a >，且b c >，那么c a >B. 如果b a >，且b c >，那么bc ac >C. 如果b a ->，那么b c a c +<-D. 如果b a >，那么bc ac >3．已知0,0<>>b b a ，下列不等式成立的是 （ ）A.b a b a ->->> B. a b b a ->>-> C. b b a a ->>-> D. b a b a >>->-4．已知22πβαπ≤≤<-，则βα-的取值范围是 （ ） A.0<-≤-βαπ B. 0≤-<-βαπ C. πβαπ<-<- D. πβαπ≤-≤-5．已知,c b a >>下列不等式成立的是 （ ）A.ac ab >B. c b c a >C.bc ab >D. )()(2222c b b c b a +>+6． 给出下列命题，其中正确的是 （ ）①若11>x，则1<x ②若y a x a 22>，则y x > ③011<<b a ，则2b ab < ④ ,0<<b a 则3322,b a b a <> A. ①② B. ②③ C. ②③④ D.①②③④7、已知24,31<<-<<b a 则b a -的取值范围是 。

高中数学 不等式的基本性质 习题1．已知a ＞b ＞c ，a ＋b ＋c ＝0，则必有( )．A ．a ≤0 B．a ＞0 C ．b ＝0 D ．c ＞02．若a ＜1，b ＞1，那么下列命题中正确的是( )．A ．11a b >B ．1b a> C ．a 2＜b 2 D ．ab ＜a ＋b －13．设a ＞1＞b ＞－1，则下列不等式中恒成立的是( )．A ．11a b <B ．11a b> C ．a ＞b 2 D ．a 2＞2b 4．已知1≤a ＋b ≤5，－1≤a －b ≤3，则3a －2b 的取值范围是( )．A ．B ．C ．D ．5．已知a ＜0，b ＜－1，则下列不等式成立的是( )．A ．2a a a b b >> B ．2a a a b b >> C ． 2a a a b b >> D ．2a a a b b>> 6．已知－3＜b ＜a ＜－1，－2＜c ＜－1，则(a －b )c 2的取值范围是__________． 7．若a ，b ∈R ，且a 2b 2＋a 2＋5＞2ab ＋4a ，则a ，b 应满足的条件是__________．8．设a ＞b ＞c ＞0，x =y =，z =x ，y ，z 之间的大小关系是__________．9．某次数学测验，共有16道题，答对一题得6分，答错一题倒扣2分，不答则不扣分，某同学有一道题未答，那么这个学生至少答对多少题，成绩才能在60分以上？列出其中的不等关系．10．已知等比数列{a n }中，a 1＞0，q ＞0，前n 项和为S n ，试比较33S a 与55S a 的大小．参考答案1. 答案：B 解析：由a ＞b ＞c ，a ＋b ＋c ＝0知3a ＞0，故a ＞0.2. 答案：D 解析：由a ＜1，b ＞1得a －1＜0，b －1＞0，所以(a －1)(b －1)＜0，展开整理即得ab ＜a ＋b －1.3. 答案：C 解析：取a ＝2，b ＝12-，满足a ＞1＞b ＞－1，但11a b>，故A 错；取a ＝2，13b =，满足a ＞1＞b ＞－1，但11a b <，故B 错；取54a =，56b =，满足a ＞1＞b ＞－1，但a 2＜2b ，故D 错，只有C 正确.4. 答案：D 解析：令3a －2b ＝m (a ＋b )＋n (a －b )，则32m n m n +=⎧⎨-=-⎩，，所以125.2m n ⎧=⎪⎪⎨⎪=⎪⎩， 又因为1≤a ＋b ≤5，－1≤a －b ≤3， 所以115()222a b ≤+≤，5515()222a b -≤-≤， 故－2≤3a －2b ≤10. 5. 答案：C 解析：∵a ＜0，b ＜－1，则0a b >，b ＜－1，则b 2＞1，∴211b <. 又∵a ＜0，∴0＞2a b＞a .∴2a a a b b >>.故选C. 6. 答案：(0,8) 解析：依题意0＜a －b ＜2,1＜c 2＜4，所以0＜(a －b )c 2＜8. 7. 答案：a ≠2或b ≠12 解析：原不等式可化为(ab －1)2＋(a －2)2＞0.故a ≠2或b ≠12. 8. 答案：x ＜y ＜z 解析：x 2－y 2＝a 2＋(b ＋c )2－b 2－(c ＋a )2＝2c (b －a )＜0，所以x ＜y ，同理可得y ＜z ，故x ，y ，z 之间的大小关系是x ＜y ＜z .9. 答案：解：设至少答对x 题，则6x －2(15－x )≥60.10. 答案：解：当q ＝1时，333S a =，555S a =，所以3535S S a a <； 当q ＞0且q ≠1时，353511243511(1)(1)(1)(1)S S a q a q a a a q q a q q ---=---＝23544(1)(1)10(1)q q q q q q q -----=<-， 所以有3535S S a a <.综上可知有3535S S a a <.。

等式性质与不等式性质同步练习一、本节知识点（1）两个实数的大小比较.（2）不等式22b a +≥ab 2的探究.（3）不等式的基本性质.二、本节题型（1）比较两个代数式的大小.（2）利用不等式的性质证明不等式.（3）利用不等式的性质求取值范围.三、同步练习 1. 完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设请木工x 人,瓦工y 人,则满足的关系式是 【 】（A ）20045<+y x （∈y x ,N *） （B ）y x 45+≥200（∈y x ,N *）（C ）20045=+y x （∈y x ,N *） （D ）y x 45+≤200（∈y x ,N *）2. 设1,2--==x N x M ,则M 与N 的大小关系是 【 】（A ）N M > （B ）N M =（C ）N M < （D ）与x 有关3. 设∈b a ,R ,且b a >,则 【 】（A ）bc ac > （B ）ba 11< （C ）22b a > （D ）33b a >4. 若0,0<<>>d c b a ,则一定有 【 】（A ）c bd a > （B ）cb d a < （C ）d bc a > （D ）d b c a < 5. 若11<<<-βα,则下列各式中恒成立的是 【 】（A ）02<-<-βα （B ）12-<-<-βα（C ）01<-<-βα （D ）11<-<-βα6. 已知c b a >>,且0=++c b a ,则下列不等式恒成立的是 【 】（A ）bc ab > （B ）bc ac > （C ）ac ab > （D ）c b b a >7. 已知实数c b a ,,满足2244,346a a b c a a c b +-=-+-=+,则c b a ,,的大小关系是 【 】（A ）c ≥a b > （B ）c a >≥b（C ）a b c >> （D ）b c a >>8.（多选）设b a ,为正实数,下列命题中的真命题是 【 】（A ）若122=-b a ,则1<-b a（B ）若111=-ab ,则1<-b a （C ）若1=-b a ,则1<-b a（D ）若133=-b a ,则1<-b a9. 有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积（单位: m 2）分别为z y x ,,,且z y x <<,三种颜色涂料的粉刷费用（单位: 元/m 2）分别为c b a ,,,且c b a <<.在不同的方案中,最低的总费用（单位: 元）是 【 】（A ）cz by ax ++ （B ）cx by az ++（C ）cx bz ay ++ （D ）cz bx ay ++10. 如果10,0<<<y x ,那么xx y x y 1,,2从小到大的顺序是_____________. 11. 比较大小:222c b a ++_________()42-++c b a .12. 若810<<<-b a ,则b a +的取值范围是_____________.13. 若已知1-≤b a +≤1,1≤b a 3-≤2,则b a 2+的取值范围是_____________.14. 已知41<+<-y x ,且32<-<y x ,则y x 32-的取值范围是_____________.15. 已知4230<<x ,2416<<y ,分别求y x +,y x 3-及yx x 3-的取值范围.16. （1）已知x ≤1,比较33x 与132+-x x 的大小; （2）若01<<<-b a ,试比较22,,1,1b a ba 的大小.17. 已知0,0>>b a ,且b a ≠,比较ab b a 22+与b a +的大小.18. 设32<<a ,34-<<-b ,求b a +,b a -,ba ,ab ,a b 2的取值范围.19. 为响应国家提出的全民健身运动,青岛二中甲、乙两位学生在周末进行体育锻炼.他们同时从学校到五四广场,甲一半路步行,一半路跑步;乙一半时间步行,一半时间跑步,如果两人步行速度相同,跑步速度也相同,试分析比较两个人谁先到达五四广场?（写出必要的分析步骤）20.某矿山车队有4辆载重10 t的甲型卡车和7辆载重6 t的乙型卡车,且有9名驾驶员,此车队每天至少要运360 t矿石到冶炼厂,已知甲型卡车每天可往返6次,乙型卡车每天可往返8次,设每天派出甲型卡车x辆,乙型卡车y辆,写出所有满足上述不等关系的关于yx,的不等式.四、答案解析等式性质与不等式性质同步练习答案解析1. 完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设请木工x 人,瓦工y 人,则满足的关系式是 【 】（A ）20045<+y x （∈y x ,N *） （B ）y x 45+≥200（∈y x ,N *）（C ）20045=+y x （∈y x ,N *） （D ）y x 45+≤200（∈y x ,N *） 解析: 由题意可得:y x 400500+≤20 000,且∈y x ,N *∴y x 45+≤200（∈y x ,N *）.∴选择答案【 D 】.2. 设1,2--==x N x M ,则M 与N 的大小关系是 【】 （A ）N M > （B ）N M =（C ）N M < （D ）与x 有关解析: 本题可采用作差法比较大小.用作差法比较大小的一般步骤为:（1）作差;（2）变形: 对差进行变形.（3）判号: 判断差的符号（如果差中含有参数,则需要进行分类讨论）.（4）定论: 根据差的符号作出大小判断.即: 作差→变形→判号→定论.作差法的关键在于变形,常用的变形为:因式分解、配方、通分、分子或分母有理化等. ∵1,2--==x N x M∴()0432111222>+⎪⎭⎫ ⎝⎛+=++=---=-x x x x x N M （∈x R ）∴N M >.∴选择答案【 A 】.3. 设∈b a ,R ,且b a >,则 【】（A ）bc ac > （B ）ba 11< （C ）22b a > （D ）33b a >解析: 本题考查不等式的基本性质,必要时可举出反例.对于（A ）,根据不等式的可乘性,当0>c 时,bc ac >成立;对于（B ）,根据不等式的倒数法则,当0>ab ,且b a >时,ba 11<成立; 对于（C ）,因为b a >,所以0>-b a .又因为()()b a b a b a -+=-22,所以当0>+b a 时,22b a >成立;对于（D ）,()()()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+-=++-=-2222334321b b a b a b ab a b a b a . ∵04321,22>+⎪⎭⎫ ⎝⎛+>b b a b a ∴0>-b a∴033>-b a ,即33b a >.∴选择答案【 D 】.4. 若0,0<<>>d c b a ,则一定有 【 】（A ）c bd a > （B ）cb d a < （C ）d bc a > （D ）d b c a < 解析: 本题考查不等式的基本性质.∵0,0<<>>d c b a∴0>->-d c ∴011>->-cd 根据不等式性质的可乘性: ∴0>->-c b d a ,∴cb d a <,选项【 B 】正确. 对于（C ）、（D ）,设1,2,1,2-=-===dc b a ,则111,122-=-=-=-=d b c a ,此时db c a =; ∴选择答案【 B 】.5. 若11<<<-βα,则下列各式中恒成立的是 【 】（A ）02<-<-βα （B ）12-<-<-βα（C ）01<-<-βα （D ）11<-<-βα解析: 本题考查不等式性质中的可加性和可乘性.∵11<<<-βα∴11,11<<-<<-βα∴11<-<-β根据不等式性质的可加性:22<-<-βα.∵βα<,∴0<-βα.∴02<-<-βα.∴选择答案【 A 】.6. 已知c b a >>,且0=++c b a ,则下列不等式恒成立的是 【 】（A ）bc ab > （B ）bc ac > （C ）ac ab > （D ）c b b a > 解析: ∵c b a >>,且0=++c b a∴0,0<>c a ,b 的符号不确定.对于（A ）,显然,当0=b 或0<b 时,bc ab >不成立;对于（B ）,∵0,<>c b a ,∴bc ac <;对于（C ）,∵0,>>a c b ,∴ac ab >成立;对于（D ）,当0=b 时,显然c b b a >不成立.∴选择答案【 C 】.7. 已知实数c b a ,,满足2244,346a a b c a a c b +-=-+-=+,则c b a ,,的大小关系是 【 】（A ）c ≥a b > （B ）c a >≥b（C ）a b c >> （D ）b c a >>解析: 本题考查作差法比较两个代数式的大小.∵()22244a a a b c -=+-=-≥0 ∴c ≥b .∵2244,346a a b c a a c b +-=-+-=+∴2222+=a b∴12+=a b ∴04321122>+⎪⎭⎫ ⎝⎛-=+-=-a a a a b ∴a b >,∴c ≥a b >.∴选择答案【 A 】.8.（多选）设b a ,为正实数,下列命题中的真命题是 【 】（A ）若122=-b a ,则1<-b a（B ）若111=-ab ,则1<-b a （C ）若1=-b a ,则1<-b a（D ）若133=-b a ,则1<-b a解析: 本题综合性较强,难度较高,可采用特殊值法快速判断正确性.对于（A ）,由122=-b a 得:221b a +=,∵b a ,为正实数,∴12>a ,∴1,1>+>b a a . ∴11<+=-ba b a ,故（A ）正确; 对于（B ）,由111=-a b 得:1+=a a b .取32,2==b a ,则134322>=-=-b a .故（B ）错误.对于（C ）,取4,9==b a ,则1549>=-=-b a ,故（C ）错误;对于（D ）,∵()()()()=+-->++-=++-=-222222332b ab a b a b ab a b a b ab a b a b a ()32b a b a b a -=-- ∴13<-b a ,∴1<-b a .故（D ）正确.综上所述,选择答案【 AD 】.9. 有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积（单位: m 2）分别为z y x ,,,且z y x <<,三种颜色涂料的粉刷费用（单位: 元/m 2）分别为c b a ,,,且c b a <<.在不同的方案中,最低的总费用（单位: 元）是 【 】（A ）cz by ax ++ （B ）cx by az ++（C ）cx bz ay ++ （D ）cz bx ay ++解析: 本题可采用特殊值法给出快速且正确的判断.方法一: 由题意可设3,2,1,3,2,1======c b a z y x ,则有:（A ）14941332211=++=⨯+⨯+⨯=++cz by ax ;（B ）10343132231=++=⨯+⨯+⨯=++cx by az ;（C ）11362133221=++=⨯+⨯+⨯=++cx bz ay ;（D ）139********=++=⨯+⨯+⨯=++cz bx ay .∵14131110<<<∴最低的总费用是cx by az ++（元）.∴选择答案【 B 】.方法二: （A ）与（B ）比较大小:()()()()()c a z x x z c z x a cx cz az ax cx by az cz by ax --=-+-=-+-=++-++ ∵c a z x <<,,∴()()0,0,0>--<-<-c a z x c a z x .∴>++cz by ax cx by az ++,即（A ）>（B ）;（C ）与（D ）比较大小:()()()()()c b x z x z c x z b cz cx bx bz cz bx ay cx bz ay --=---=-+-=++-++ ∵c b z x <<,,∴()()0,0,0<--<->-c b x z c b x z .∴cz bx ay cx bz ay ++<++,即（C ）<（D ）;最后,（B ）与（C ）比较大小:-++cx by az ()()()()()b a y z z y b y z a cx bz ay --=-+-=++∵b a z y <<,,∴()()0,0,0<--<->-b a y z b a y z .∴<++cx by az cx bz ay ++,即（B ）<（C ）.∴选择答案【 B 】.10. 如果10,0<<<y x ,那么xx y x y 1,,2从小到大的顺序是_____________. 解析: xy x x y 11-=- ∵10,0<<<y x ,∴01,01>-<-x y y ,∴x x y 1>. ()xy y x y y x y x y 122-=-=- ∵10,0<<<y x ,∴()()01,01>-<-xy y y y ,∴x y x y >2. ∴xy x y x 21<<. 方法二（特殊值法）:∵10,0<<<y x ,∴令21,1=-=y x . ∴41121,21121,111122-=-⎪⎭⎫ ⎝⎛=-=-=-=-=x y x y x . ∵41211-<-<- ∴xy x y x 21<<. 11. 比较大小:222c b a ++_________()42-++c b a .解析: 本题采用作差法比较大小.()[]()()()1121212422242222222222++-++-++-=+---++=-++-++c c b b a a c b a c b a c b a c b a=()()()1111222+-+-+-c b a ∵()()()01111222>+-+-+-c b a ∴>++222c b a ()42-++c b a .12. 若810<<<-b a ,则b a +的取值范围是_____________.解析: 本题考查不等式性质中的同向可加性.∵810<<<-b a∴0≤10<a ,810<<-b ∴1810<+<-b a ∵a a b a +>+≥0 ∴180<+<b a ∴b a +的取值范围是{}180<+<+b a b a .13. 若已知1-≤b a +≤1,1≤b a 3-≤2,则b a 2+的取值范围是_____________. 解析: 本题已知两个关于b a ,线性关系的代数式的取值范围,求另一个关于b a ,线性关系的代数式的取值范围,使用待定系数法.设()()b a n b a m b a 32-++=+,∴()()b a b n m a n m 23+=-++∴⎩⎨⎧=-=+231n m n m ,解之得:⎪⎪⎩⎪⎪⎨⎧-==4145n m ∴()()b a b a b a 341452--+=+. ∵1-≤b a +≤1,1≤b a 3-≤2 ∴45-≤()b a +45≤45,21-≤()b a 341--≤41- ∴47-≤()()b a b a 34145--+≤1 ∴b a 2+的取值范围是⎭⎬⎫⎩⎨⎧≤+≤-+12472b a b a .点拨 上述方法称为待定系数法,具有一般性,必须掌握.本题切记不可单独求出b a ,的取值范围,再求b a 2+的取值范围,此时所得的范围与实际范围不一致.14. 已知41<+<-y x ,且32<-<y x ,则y x 32-的取值范围是_____________. 解析: 本题同第13题.设()()y x n y x m y x -++=-32,∴()()y n m x n m y x -++=-32∴⎩⎨⎧-=-=+32n m n m ,解之得:⎪⎪⎩⎪⎪⎨⎧=-=2521n m ∴()()y x y x y x -++-=-252132 ∵41<+<-y x ,32<-<y x ∴()()215255,21212<-<<+-<-y x y x ∴()()825213<-++-<y x y x ,即8323<-<y x . ∴y x 32-的取值范围是{}832332<-<-y x y x .15. 已知4230<<x ,2416<<y ,分别求y x +,y x 3-及yx x 3-的取值范围. 解: ∵4230<<x ,2416<<y ∴48372,24421630-<-<-+<+<+y y x∴6646<+<y x .∴484237230-<-<-y x ,∴6342-<-<-y x . ∴4213161-<-<-y x （倒数法则）. ∴6131421<--<y x ,∴6142342130⨯<--<⨯y x x （同向同正可乘性） ∴7375<--<y x x ,∴7537-<-<-y x x .∴y x +的取值范围是{}6646<+<+y x y x ,y x 3-的取值范围是{}63423-<-<--y x y x ,y x x 3-的取值范围是⎭⎬⎫⎩⎨⎧-<-<--75373y x x yx x . 16. （1）已知x ≤1,比较33x 与132+-x x 的大小;（2）若01<<<-b a ,试比较22,,1,1b a ba 的大小. 解:（1）()13323+--x x x ()()()()1311131332223+-=-+-=-+-=x x x x x x x x .∵x ≤1,∴1-x ≤0,0132>+x∴()()1312+-x x ≤0∴33x ≤132+-x x ;（2）∵01<<<-b a ,∴111-<<ab （倒数法则）,0,022>>b a . ∵()()b a b a b a -+=-22,0,0<-<+b a b a∴022>-b a ,∴22b a >. ∴2211a b ab <<<. 17. 已知0,0>>b a ,且b a ≠,比较ab b a 22+与b a +的大小. 解: ()b a ab b a +-+22 ()abab b a b a ab b a ab ab b a 223333--+=+-+= ()()()()ab b a b a ab b a b a +-=--=222.∵0,0>>b a ,且b a ≠∴()0,0,02>>+>-ab b a b a∴()()02>+-ab b a b a ∴b a ab b a +>+22. 18. 设32<<a ,34-<<-b ,求b a +,b a -,ba ,ab ,a b 2的取值范围. 解: ∵32<<a ,34-<<-b ,∴43<-<b∴3342-<+<-b a ,4332+<-<+b a∴75,02<-<<+<-b a b a .∵43<-<b ,∴31141<-<b ∴121,313412<-<⨯<-<⨯ba b a ∴211-<<-b a . ∵32<<a ,43<-<b ,∴126<-<ab∴612-<<-ab .∵32<<a ,43<-<b ∴21131<<a ,()169,443322<<⨯<-<⨯b b ∴16219312⨯<<⨯a b ∴832<<ab . ∴b a +的取值范围是{}02<+<-+b a b a ,b a -的取值范围是{}75<-<-b a b a ,b a 的取值范围是⎭⎬⎫⎩⎨⎧-<<-211b a b a , ab 的取值范围是{}612-<<-ab ab ,a b 2的取值范围是⎭⎬⎫⎩⎨⎧<<8322a b a b .19. 为响应国家提出的全民健身运动,青岛二中甲、乙两位学生在周末进行体育锻炼.他们同时从学校到五四广场,甲一半路步行,一半路跑步;乙一半时间步行,一半时间跑步,如果两人步行速度相同,跑步速度也相同,试分析比较两个人谁先到达五四广场?（写出必要的分析步骤）解: 设他们步行的速度为1v ,跑步的速度为2v ,学校到五四广场的路程为2,则有:21212111v v v v v v t +=+=甲,2212121=+乙乙t v t v ∴214v v t +=乙. ∴()()04141-2122121221>-=-+=v v v v v v v v t t 乙甲 ∴01>-乙甲t t ,即1>乙甲t t ,乙甲t t >. ∴乙先到达五四广场.答:乙先到达五四广场.实际上,()()042121221212121>+-=+-+=-v v v v v v v v v v v v t t 乙甲,所以乙甲t t >. 20. 某矿山车队有4辆载重10 t 的甲型卡车和7辆载重6 t 的乙型卡车,且有9名驾驶员,此车队每天至少要运360 t 矿石到冶炼厂,已知甲型卡车每天可往返6次,乙型卡车每天可往返8次,设每天派出甲型卡车x 辆,乙型卡车y 辆,写出所有满足上述不等关系的关于y x ,的不等式.解: 由题意可得:⎪⎪⎩⎪⎪⎨⎧∈≤≤∈≤≤≥+≤+Ny y N x x y x y x ,70,4036048609.。

第06讲 等式性质与不等式性质模块一 思维导图串知识模块二 基础知识全梳理（吃透教材）模块三 核心考点举一反三模块四 小试牛刀过关测1．通过用不等式（组)表示实际问题，提升数学抽象与数学建模素养；2．通过比较两个实数的大小、不等式性质的应用，提升逻辑推理、数学运算素养；3．运用不等式的性质解决有关问题．知识点 1 不等关系与不等式1、不等式的概念（1）用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式，以表示它们之间的不等式关系，含有这些不等式号的式子，叫做不等式．（2）用“<”或“>”连接的不等式叫严格不等式；用“≤”或“≥”连接的不等式叫非严格不等式．2、常见文字语言与符号语言之间的对应关系文字语言大于、高于、超过小于、低于、少于大于或等于、至少、不低于小于或等于、至多、不多于、不超过符号语言><≥≤3、用不等式组表示不等式关系当问题情境中包含两个或两个以上的不等式关系时，需要用不等式组来表示不等关系．知识点 2 等式性质性质文字表述性质内容注意1对称性a b b a=⇔=可逆2传递性,a b b c a c==⇒=同向3可加、减性a b a c b c =⇔±=±可逆4可乘性a b ac bc=⇒=同向5可除性,0a b a b c c c=≠⇒=同向知识点 3 不等式性质性质别名性质内容注意1对称性a >b ⇔b <a 可逆2传递性a >b ，b >c ⇒a >c 同向3可加性a >b ⇔a ＋c >b ＋c 可逆4可乘性a >b ，c >0⇒ac >bc a >b ，c <0⇒ac <bc c 的符号5同向可加性a >b ，c >d ⇒a ＋c >b ＋d 同向6正数同向可乘性a >b >0，c >d >0⇒ac >bd 同向7正数乘方性a >b >0⇒a n >b n (n ∈N ，n ≥2)同正知识点 4 比较大小的方法1、作差法、作商法是比较两个实数（或代数式）大小的基本方法．①作差法的步骤：作差、变形、判断差的符号、得出结论．②作商法的步骤：作商、变形、判断商与1的大小、得出结论．2、介值比较法也是比较大小的常用方法，其实质是不等式的传递性：若a ＞b ，b ＞c ，则a ＞c ；若a ＜b ，b ＜c ，那么a ＜c ．其中b 是介于a 与c 之间的值，此种方法的关键是通过恰当的放缩，找出一个比较合适的中介值．3、平方法：对两式先平方，再比较大小．【注意】（1）比较代数式的大小通常采用作差法，如果含有根式，也可以先平方再作差，但此时一定要保证代数式大于零；（2）作差时应该对差式进行恒等变形（如配方、因式分解、有理化、通分等），直到能明显看出其正负号为止；（3）作商法适合于幂式、积式、分式间的大小比较，作商后应变形为能与“1”比较大小的式子，要注意营养函数的有关性质．考点一：用不等式（组）表示不等式关系例1．（23-24高一上·广东深圳·月考）公司运输一批木材，总重600吨，车队有两种货车，A 型货车载重量30吨，B 型货车载重量24吨，设派出A 型货车x 辆，B 型货车y 辆，则运输方案应满足的关系式是（ ）A ．54100x y +<B ．54100x y +≥C ．54100x y +>D ．54100x y +≤【变式1-1】（23-24高一上·贵州遵义·月考）持续的高温干燥天气导致某地突发山火，现需将物资运往灭火前线．从物资集散地到灭火前线-共40km ，其中靠近灭火前线5km 的山路崎岖，需摩托车运送，其他路段可用汽车运送．已知在可用汽车运送的路段，运送的平均速度为60km h ，设需摩托车运送的路段平均速度为km h x ，为使物资能在1小时内到达灭火前线，则x 应该满足的不等式为（ ）．A ．40160x>+B ．40160x<+C ．355160x+>D ．355160x+<【变式1-2】（22-23高一上·甘肃酒泉·期末）铁路总公司关于乘车行李规定如下：乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过130cm ，且体积不超过372000cm ，设携带品外部尺寸长、宽、高分别记为a ，b ，c （单位：cm ），这个规定用数学关系式可表示为（ ）A ．130a b c ++<且72000abc <B ．130a b c ++>且72000abc >C ．130a b c ++≤且72000abc ≤D ．130a b c ++≥且72000abc ≥【变式1-3】（22-23高一上·四川眉山·月考）将一根长为5m 的绳子截成两段，已知其中一段的长度为x m ，若两段绳子长度之差不小于1m ，则x 所满足的不等关系为（ ）A ．25005x x ->⎧⎨<<⎩B ．251x -≥或521x -≥C ．52105x x -≥⎧⎨<<⎩D ．25105x x ⎧-≥⎨<<⎩考点二：比较实数（代数式）的大小例2. （23-24高一上·河南洛阳·期末）今年某地因天气干旱导致白菜价格不稳定，假设第一周、第二周的白菜价格分别为a 元/斤、b 元/斤()a b ≠，王大妈每周购买10元的白菜，李阿姨每周购买8斤白菜，王大妈和李阿姨两周买白菜的平均价格分别记为1m ，2m ，则1m 与2m 的大小关系为（ ）A ．12m m =B ．12m m >C ．12m m <D ．无法确定【变式2-1】（23-24高一上·江苏常州·期末）设a ，b ，m 都是正数，且a b <，记,a m ax y b m b +==+，则（ ）A ．x y >B ．x y=C ．x y< D ．x 与y 的大小与m的取值有关【变式2-2】（23-24高一上·陕西榆林·月考）设0a b >>，比较2222a b a b -+与a b a b -+的大小【变式2-3】（23-24高一上·山东青岛·月考）已知0a >，0b >的大小；考点三：利用不等式的性质判断命题真假例3. （23-24高一上·河北石家庄·月考）若||||a b >，则下列不等式成立的是（ ）A ．0a b ->B ．11a b<C ．a b >D ．22a b >【变式3-1】（23-24高一上·内蒙古呼和浩特·期中）下列说法正确的是（ ）A ．若a b >，则22ac bc >B ．若22a bc c >，则a b >C ．若a b >，cd >，则ac bd>D ．若0b a >>，则a c ab c b+>+【变式3-2】（23-24高一上·吉林延边·月考）（多选）下列结论错误的是（）A ．若a b >，则ac bc <B ．若a b >，则11a b <C ．若a b >，则22a b >D ．若22ac bc >，则a b>【变式3-3】（23-24高一上·广西贺州·期末）（多选）若0a b >>，0c <，则下列不等关系正确的是（ ）A ．a c b c+>+B ．22a bc c >C ．ac bc >D ．11a b b a+>+考点四：利用不等式的性质求范围例4. （23-24高一上·陕西咸阳·月考）已知23a <<，21b -<<-，则2a b -的取值范围是（ ）A ．[]6,7B ．()2,5C ．[]4,7D ．()5,8【变式4-1】（23-24高一上·江西景德镇·月考）已知3b a b <<-，则ab的取值范围为（ ）A ．03ab<<B ．03a b≤<C ．3a b >D ．13a b<<【变式4-2】（23-24高一上·河北石家庄·期中）已知14a b ≤+≤，12a b -≤-≤，则42a b -的取值范围是（ ）A ．{}410x x -<<B ．{}36x x -<<C ．{}214x x -<<D ．{}210x x -≤≤【变式4-3】（23-24高一上·吉林四平·期中）已知2236x y ≤+≤，3569x y -≤-≤，则113z x y =+的取值范围是（ ）A ．58933z z ⎧⎫≤≤⎨⎬⎩⎭B ．5|273z z ⎧⎫≤≤⎨⎬⎩⎭C ．8933z z ⎧⎫≤≤⎨⎬⎩⎭D ．{}327z z ≤≤考点五：利用不等式的性质证明不等式例5. （23-24高一上·河北保定·月考）设,,a b c ∈R ，0a b c ++=，1abc =.(1)证明：0ab bc ca ++<；(2)若a b >，证明33a b >.【变式5-1】（23-24高一上·陕西榆林·期中）证明下列不等式：(1)已知a b c d >>>，求证：11a db c<--；(2)已知0,0,0a b c d e >><<<，求证：e e a c b d>--.【变式5-2】（23-24高一上·安徽芜湖·月考）（1）已知0b a >>，证明：2a a b b a<+；（2）若a ，b ，c 为三角形的三边长，则2a b cb c a c a b++<+++．【变式5-3】（23-24高一上·云南·月考）证明下列不等式：(1)若0,0a b >>，求证：22a ba b b a++≥；(2)若0a b >>，0c d <<，0e <，求证：()()22eea cb d >--．考点六：不等式性质的实际应用例6. （23-24高一上·四川南充·月考）火车站有某公司待运的甲种货物1530吨，乙种货物1150吨．现计划用A ，B 两种型号的货箱共50节运送这批货物．已知35吨甲种货物和15吨乙种货物可装满一节A 型货箱，25吨甲种货物和35吨乙种货物可装满一节B 型货箱，据此安排A ，B 两种货箱的节数，下列哪个方案不满足：（ ）A ．A 货箱28节，B 货箱22节B ．A 货箱29节，B 货箱21节C ．A 货箱31节，B 货箱19节D ．A 货箱30节，B 货箱20节【变式6-1】（22-23高一上·山东·月考）某化工厂制定明年某产品的生产计划，受下面条件的制约：生产每袋需用4h ；生产此产品的工人不超过200人，每个工人的年工作时间约为2100h ；生产每袋需用原料20kg ，年底库存原料600t ，明年可补充1200t ；此产品今年销售量是60000袋，预计明年的销售量至少在今年的基础上增长13．根据这些数据条件可以预测明年的产量在（ ）A ．70000到75000袋之间B ．70000到80000袋之间C ．80000到85000袋之间D ．80000到90000袋之间【变式6-2】（23-24高一上·全国·专题练习）王老师是高三的班主任，为了更好地督促班上的学生完成作业，王老师特地组建了一个学习小组的钉钉群，群的成员由学生、家长、老师共同组成．已知该钉钉群中男学生人数多于女学生人数，女学生人数多于家长人数，家长人数多于教师人数，教师人数的两倍多于男学生人数．则该钉钉群人数的最小值为（ ）A ．18B ．20C ．22D ．28【变式6-3】（23-24高一上·吉林长春·月考）不等关系是数学中一种最基本的数关系，生活中随处可见.例如.已知b 克糖水中含有a 克糖(0)b a >>，再添加m 克糖(0)m >(假设全部溶解)，糖水变甜了.(1)请将这一事实表示为一个不等式.并证明这个不等式成立：(2)利用（1）中的结论证明：若,,a b c 为三角形的三边长，则2a b cb c a c a b++<+++.一、单选题1．（22-23高一上·河北邢台·月考）在开山工程爆破时，已知导火索燃烧的速度是每秒0.5厘米，人跑开的速度为每秒4米，距离爆破点150米以外（含150米）为安全区．为了使导火索燃尽时人能够跑到安全区，导火索的长度x （单位：厘米）应满足的不等式为（ ）A ．41500.5x⨯<B ．41500.5x⨯≥C ．41500.5x⨯≤D ．41500.5x⨯>2．（23-24高一上·云南昆明·期中）设2254M a a =++，(1)(3)N a a =++，则M 与N 的大小关系为（ ）A ．M N>B ．M N=C ．M N<D ．无法确定3．（23-24高一上·广东深圳·期末）已知,,R,a b c a b ∈>，则下列一定成立的是（ ）A ．11a b<B ．2ab b >C ．b c ba c a+>+D ．()()2211a c b c +>+4．（23-24高一上·安徽宣城·自主招生）已知实数a ，b ，则下列选项中正确的是（ ）A ．若a b >，则22a b >B ．若a b >，则22a b >C ．若a b >，则22a b >D ．若a b >，则11a b<5．（23-24高一上·河南驻马店·期末）已知15,31a b -<<-<<，则以下错误的是（ ）A ．155ab -<<B ．46a b -<+<C ．28a b -<-<D ．553ab-<<6．（23-24高一上·山东菏泽·月考）已知11x y -≤+≤，13x y ≤-≤，则32x y -的取值范围是（ ）A ．2328x y ≤-≤B ．3328x y ≤-≤C ．2327x y ≤-≤D ．53210x y ≤-≤二、多选题7．（23-24高一上·山东日照·期末）若实数a ，b ，c 满足()0a b b >≠且0a >，0c >，则下列不等式正确的是（ ）A ．11a b<B ．ac bc-<-C ．b c ba c a+>+D ．22222b a a b+>8．（23-24高一上·四川乐山·期中）下列不等式中，一定成立的是（ ）A ．若0,a b c >>∈R ，则22c ca b<B ．若0,a b c >>∈R ，则22ac bc >C ．若0a b <<，则22a ab b >>D ．若0a b <<，则22a a b b+<+三、填空题9．（23-24高一上·广东韶关·月考）已知x ∈R ，则23x + 2x .（填“<”，“>”，或“=”）10．（23-24高一上·北京西城·期中）已知a ，b ，c 为实数，能说明“若a b c >>，则2a bc >”为假命题的一组a ，b ，c 的值是.11．（23-24高一上·山东菏泽·期中）“双节”遇上亚运会，民宿成为潮流趋势．民宿的改造中，窗户面积与地板面积之比越大，采光效果越好．现有一所地板面积为180平方米的民宿需要同时增加窗户和地板的面积，已知地板增加的面积是窗户增加的面积的2倍，且民宿改造后的采光效果不逊于改造前，则改造前的窗户面积最大为平方米．四、解答题12．（23-24高一上·福建泉州·月考）（1）已知R a ∈，设()21M a a =+，()()21N a a =+-，比较M 与N 的大小；（2）证明：已知a b c >>，且0a b c ++=，求证：c ca cb c>--.13．（23-24高一上·湖北·期中）（1）已知b 克糖水中含有a 克糖（0b a >>），再添加m 克糖（0m >）（假设全部溶解），糖水变甜了.请将这一事实表示为一个不等式，不必证明.利用此结论证明：若,,a b c 为三角形的三边长，则2a b cb c a c a b++<+++.（2）超市里面提供两种糖：白糖每千克1p 元，红糖每千克2p 元()12p p ≠.小东买了相同质量的两种糖，小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高？请证明你的结论.（物品的平均价格=物品的总价钱÷物品的总质量）第06讲 等式性质与不等式性质模块一 思维导图串知识模块二 基础知识全梳理（吃透教材）模块三 核心考点举一反三模块四 小试牛刀过关测1．通过用不等式（组)表示实际问题，提升数学抽象与数学建模素养；2．通过比较两个实数的大小、不等式性质的应用，提升逻辑推理、数学运算素养；3．运用不等式的性质解决有关问题．知识点 1 不等关系与不等式1、不等式的概念（1）用数学符号“≠”“>”“<”“≥”“≤”连接两个数或代数式，以表示它们之间的不等式关系，含有这些不等式号的式子，叫做不等式．（2）用“<”或“>”连接的不等式叫严格不等式；用“≤”或“≥”连接的不等式叫非严格不等式．2、常见文字语言与符号语言之间的对应关系文字语言大于、高于、超过小于、低于、少于大于或等于、小于或等于、至多、至少、不低于不多于、不超过符号语言><≥≤3、用不等式组表示不等式关系当问题情境中包含两个或两个以上的不等式关系时，需要用不等式组来表示不等关系．知识点 2 等式性质性质文字表述性质内容注意1对称性a b b a=⇔=可逆2传递性,a b b c a c==⇒=同向3可加、减性a b a c b c =⇔±=±可逆4可乘性a b ac bc=⇒=同向5可除性,0a b a b c c c=≠⇒=同向知识点 3 不等式性质性质别名性质内容注意1对称性a >b ⇔b <a 可逆2传递性a >b ，b >c ⇒a >c 同向3可加性a >b ⇔a ＋c >b ＋c 可逆4可乘性a >b ，c >0⇒ac >bc a >b ，c <0⇒ac <bc c 的符号5同向可加性a >b ，c >d ⇒a ＋c >b ＋d 同向6正数同向可乘性a >b >0，c >d >0⇒ac >bd 同向7正数乘方性a >b >0⇒a n >b n (n ∈N ，n ≥2)同正知识点 4 比较大小的方法1、作差法、作商法是比较两个实数（或代数式）大小的基本方法．①作差法的步骤：作差、变形、判断差的符号、得出结论．②作商法的步骤：作商、变形、判断商与1的大小、得出结论．2、介值比较法也是比较大小的常用方法，其实质是不等式的传递性：若a ＞b ，b ＞c ，则a ＞c ；若a ＜b ，b ＜c ，那么a ＜c ．其中b 是介于a 与c 之间的值，此种方法的关键是通过恰当的放缩，找出一个比较合适的中介值．3、平方法：对两式先平方，再比较大小．【注意】（1）比较代数式的大小通常采用作差法，如果含有根式，也可以先平方再作差，但此时一定要保证代数式大于零；（2）作差时应该对差式进行恒等变形（如配方、因式分解、有理化、通分等），直到能明显看出其正负号为止；（3）作商法适合于幂式、积式、分式间的大小比较，作商后应变形为能与“1”比较大小的式子，要注意营养函数的有关性质．考点一：用不等式（组）表示不等式关系例1．（23-24高一上·广东深圳·月考）公司运输一批木材，总重600吨，车队有两种货车，A 型货车载重量30吨，B 型货车载重量24吨，设派出A 型货车x 辆，B 型货车y 辆，则运输方案应满足的关系式是（ ）A ．54100x y +<B ．54100x y +≥C ．54100x y +>D ．54100x y +≤【答案】B【解析】由已知可得，3024600x y +≥，所以有54100x y +≥.故选：B.【变式1-1】（23-24高一上·贵州遵义·月考）持续的高温干燥天气导致某地突发山火，现需将物资运往灭火前线．从物资集散地到灭火前线-共40km ，其中靠近灭火前线5km 的山路崎岖，需摩托车运送，其他路段可用汽车运送．已知在可用汽车运送的路段，运送的平均速度为60km h ，设需摩托车运送的路段平均速度为km h x ，为使物资能在1小时内到达灭火前线，则x 应该满足的不等式为（ ）．A ．40160x>+B ．40160x<+C ．355160x+>D ．355160x+<【答案】D【解析】由题意汽车所用时间加上摩托车所用时间小于1小时，即355160x+<，故选：D ．【变式1-2】（22-23高一上·甘肃酒泉·期末）铁路总公司关于乘车行李规定如下：乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过130cm ，且体积不超过372000cm ，设携带品外部尺寸长、宽、高分别记为a ，b ，c （单位：cm ），这个规定用数学关系式可表示为（ ）A ．130a b c ++<且72000abc <B ．130a b c ++>且72000abc >C ．130a b c ++≤且72000abc ≤D ．130a b c ++≥且72000abc ≥【答案】C【解析】由长、宽、高之和不超过130cm 得130a b c ++≤，由体积不超过372000cm 得72000abc ≤.故选：C.【变式1-3】（22-23高一上·四川眉山·月考）将一根长为5m 的绳子截成两段，已知其中一段的长度为x m ，若两段绳子长度之差不小于1m ，则x 所满足的不等关系为（ ）A ．25005x x ->⎧⎨<<⎩B ．251x -≥或521x -≥C ．52105x x -≥⎧⎨<<⎩D ．25105x x ⎧-≥⎨<<⎩【答案】D【解析】由题意,可知另一段绳子的长度为()5m x -.因为两段绳子长度之差不小于1m ，所以()5105x x x ⎧--≥⎪⎨<<⎪⎩，化简得：25105x x ⎧-≥⎨<<⎩.故选：D考点二：比较实数（代数式）的大小例2. （23-24高一上·河南洛阳·期末）今年某地因天气干旱导致白菜价格不稳定，假设第一周、第二周的白菜价格分别为a 元/斤、b 元/斤()a b ≠，王大妈每周购买10元的白菜，李阿姨每周购买8斤白菜，王大妈和李阿姨两周买白菜的平均价格分别记为1m ，2m ，则1m 与2m 的大小关系为（ ）A ．12m m =B ．12m m >C ．12m m <D ．无法确定【答案】C【解析】由题意可得，0a >，0b >，a b ¹，12021010abm a b a b==++，288162a b a b m ++==，()()221224()()0222ab a b ab a b a b m m a b a b a b +-+---=-==<+++ ，12m m ∴<．故选：C ．【变式2-1】（23-24高一上·江苏常州·期末）设a ，b ，m 都是正数，且a b <，记,a m ax y b m b +==+，则（ ）A ．x y >B ．x y=C ．x y< D ．x 与y 的大小与m的取值有关【答案】A【解析】由0,0,0a b m >>>，且a b <，即0b a ->，可得()()0m b a a m a b m b x b b m y --=+-=>++，即x y >，故选：A.【变式2-2】（23-24高一上·陕西榆林·月考）设0a b >>，比较2222a b a b -+与a b a b -+的大小【答案】2222a b a ba b a b-->++【解析】00,0a b a b a b >>⇒+>-> ，()()2222220,0a b a b a b a b a b a b a b +---∴=>>+++，222222222()211a b a b ab a b a b a b a b a b-++∴==+>-+++，2222a b a ba b a b--∴>++.【变式2-3】（23-24高一上·山东青岛·月考）已知0a >，0b >的大小；≤a b =时取等号）=()()3322x y x y x xy y +=+-+，可得分子)33a b =+=，a b+==进一步对其分子利用基本不等式可得a b+≥=，且等号成立当且仅当a b =，1≥，≤a b =时取等号）.考点三：利用不等式的性质判断命题真假例3. （23-24高一上·河北石家庄·月考）若||||a b >，则下列不等式成立的是（ ）A ．0a b ->B ．11a b<C ．a b >D ．22a b >【答案】D【解析】因为||||a b >，所以22a b >，D 正确；当2,1a b =-=时，满足||||a b >，但是a b <，A,C 不正确；当2,1a b =-=-时，满足||||a b >，但是11a b>，B 不正确；故选：D 【变式3-1】（23-24高一上·内蒙古呼和浩特·期中）下列说法正确的是（ ）A ．若a b >，则22ac bc >B ．若22a bc c >，则a b >C ．若a b >，c d >，则ac bd >D ．若0b a >>，则a c ab c b+>+【答案】B【解析】对于A ：当0c =时，2c =0，若a b >，则220ac bc ==，故A 错误；对于B ：因为22a b c c>，所以20c ≠，即20c >，所以a b >，故B 正确；对于C ：当1a =，0b =，1c =-，2d =-时，满足a b >，c d >，但是ac bd <，故C 错误；对于D ：当0c =时，a c ab c b+=+，故D 错误.故选：B 【变式3-2】（23-24高一上·吉林延边·月考）（多选）下列结论错误的是（）A ．若a b >，则ac bc <B ．若a b >，则11a b <C ．若a b >，则22a b >D ．若22ac bc >，则a b>【答案】AB【解析】取2,2,1a b c ==-=可得，a b >，但22ac bc =>-=，A 错误；取2,2a b ==-可得，a b >，但111122a b=>-=，B错误；因为a b >，又0b ≥，所以22a b >，故22a b >，C 正确；由22ac bc >，可得20c >，所以a b >，D 正确；故选：AB.【变式3-3】（23-24高一上·广西贺州·期末）（多选）若0a b >>，0c <，则下列不等关系正确的是（ ）A ．a c b c +>+B ．22a bc c >C ．ac bc >D ．11a b b a+>+【答案】ABD【解析】对A, 0a b >>，0c <，由不等式性质易知 a c b c +>+，故A 正确；对B, 0a b >>，0c <,则22210,a bc c c >∴>，故B 正确；对C, 0a b >>，0c <，由不等式性质易知ac bc <，故C 错误；对D, 若0a b >>，则()11110⎛⎫⎛⎫+-+=-+> ⎪ ⎪⎝⎭⎝⎭a b a b b a ab , 故D 正确.故选：ABD.考点四：利用不等式的性质求范围例4. （23-24高一上·陕西咸阳·月考）已知23a <<，21b -<<-，则2a b -的取值范围是（ ）A ．[]6,7B ．()2,5C ．[]4,7D ．()5,8【答案】D【解析】由题意可知426a <<，12b <-<，所以528<-<a b ，故选：D【变式4-1】（23-24高一上·江西景德镇·月考）已知3b a b <<-，则ab的取值范围为（ ）A ．03a b<<B ．03a b≤<C ．3a b >D ．13a b<<【答案】B【解析】因为3b a b <<-，所以0b <，则有10b<，将不等式3b a b <<-的两边同时乘1b ，可得31a b-<<，所以03a b ≤<.故选：B ．【变式4-2】（23-24高一上·河北石家庄·期中）已知14a b ≤+≤，12a b -≤-≤，则42a b -的取值范围是（ ）A ．{}410x x -<<B ．{}36x x -<<C ．{}214x x -<<D ．{}210x x -≤≤【答案】D【解析】由12a b -≤-≤，14a b ≤+≤，得()()06a b a b ≤-++≤，即026a ≤≤，()224a b -≤-≤，所以()22210a b a -≤-+≤，即24210a b -≤-≤，故选：D【变式4-3】（23-24高一上·吉林四平·期中）已知2236x y ≤+≤，3569x y -≤-≤，则113z x y =+的取值范围是（ ）A ．58933z z ⎧⎫≤≤⎨⎬⎩⎭B ．5|273z z ⎧⎫≤≤⎨⎬⎩⎭C ．8933z z ⎧⎫≤≤⎨⎬⎩⎭D ．{}327z z ≤≤【答案】D【解析】设)231156(3)(x y x x y n y m +=-++，则25)(113(36)x y m n y m n x +++=-，所以2511363m n m n +=⎧⎨-=⎩，解得31m n =⎧⎨=⎩，于是1133(56)23)(x y y x x y +++=-又63(23)18x y ≤+≤，3569x y -≤-≤，所以33(56)2723)(x y x y ++≤-≤，即311327x y ≤+≤.故{}327z z ≤≤．故选：D ．考点五：利用不等式的性质证明不等式例5. （23-24高一上·河北保定·月考）设,,a b c ∈R ，0a b c ++=，1abc =.(1)证明：0ab bc ca ++<；(2)若a b >，证明33a b >.【答案】(1)证明见解析；(2)证明见解析【解析】（1）证明:∵()22222220a b c a b c ab ac bc ++=+++++=，∴()22212ab bc ca a b c ++=-++.a ，b ，c 不同时为0，则2220a b c ++>，∴()222102ab bc ca a b c ++=-++<；（2）()()3322a b a b a ab b -=-++.∵222213024a ab b a b b ⎛⎫++=++≥ ⎪⎝⎭，取等号的条件为0a b ==，而a b >，∴等号无法取得，即222213024a b b a ab b ⎛⎫=++> ⎪⎝+⎭+，又a b >，∴()()33220a b a b a ab b -=-++>，∴33a b >.【变式5-1】（23-24高一上·陕西榆林·期中）证明下列不等式：(1)已知a b c d >>>，求证：11a db c<--；(2)已知0,0,0a b c d e >><<<，求证：e e a c b d>--.【答案】(1)证明见解析；(2)证明见解析【解析】（1）a b c d >>>Q ，即,a b d c >->-，0a d b c ∴->->，则11a db c<--.（2）0,0,0a b c d e >><<< ，0c d ∴->->，0,0,0a c b d b a c d ∴->->-<-<，则()()()()()()()()()()0e b d e a c e b d a c e b a c d e ea cb d ac bd a c b d a c b d -----+-+--===>--------，.e ea cb d∴>--【变式5-2】（23-24高一上·安徽芜湖·月考）（1）已知0b a >>，证明：2a a b b a<+；（2）若a ，b ，c 为三角形的三边长，则2a b cb c a c a b++<+++．【答案】（1）证明见解析；（2）证明见解析.【解析】（1）()()()()22a b a ab a a b a ab b a b b a b b a +---==+++，由0b a >>，得0a b -<，而0b >，0b a +>，0a >，则()()0a a b b b a -<+，所以2a ab b a<+．（2）,,a b c 为ABC 的三边长，则有0a b c +>>，0a c b +>>，0b c a +>>，由（1）知：c c c a b a b c +<+++，a a a b c a b c +<+++，b b ba c ab c+<+++，将以上不等式左右两边分别相加得：2c a b c c a a b b a b b c a c a b c a b c a b c+++++<++=+++++++++，所以2c a b a b b c c a++<+++．【变式5-3】（23-24高一上·云南·月考）证明下列不等式：(1)若0,0a b >>，求证：22a ba b b a++≥；(2)若0a b >>，0c d <<，0e <，求证：()()22eea cb d >--．【答案】(1)证明见解析；(2)证明见解析【解析】（1）证明：因为()()()2223322a b a b a b a b a b ab a b b a ab ab +-⎛⎫+--+-+== ⎪⎝⎭，又因为0,0a b >>，所以()()20a b a b ab+-≥，所以22a b a b b a++≥．（2）证明：由()()()()()()222222e b d a c eea cb d ac bd ⎡⎤---⎣⎦-=----()()()()()()22e a b c d b a c d a c b d ⎡⎤⎡⎤+-+-+-⎣⎦⎣⎦=--，因为0a b >>，0c d <<，所以0a b +>，0c d +<，0b a -<，0c d -<，所以()()0a b c d +-+>，()()0b a c d -+-<．因为0e <，所以()()()()0e a b c d b a c d ⎡⎤⎡⎤+-+-+->⎣⎦⎣⎦又因为()()220a c b d -->，所以()()220eea cb d ->--，即()()22eea cb d >--．考点六：不等式性质的实际应用例6. （23-24高一上·四川南充·月考）火车站有某公司待运的甲种货物1530吨，乙种货物1150吨．现计划用A ，B 两种型号的货箱共50节运送这批货物．已知35吨甲种货物和15吨乙种货物可装满一节A 型货箱，25吨甲种货物和35吨乙种货物可装满一节B 型货箱，据此安排A ，B 两种货箱的节数，下列哪个方案不满足：（ ）A ．A 货箱28节，B 货箱22节B ．A 货箱29节，B 货箱21节C ．A 货箱31节，B 货箱19节D ．A 货箱30节，B 货箱20节【答案】C【解析】设A 、B 货箱分别有x ，y 节，则503525153015351150x y x y x y +=⎧⎪+≥⎨⎪+≥⎩，A ：共50节且352825221530⨯+⨯=，1528352211901150⨯+⨯=>，满足；B ：共50节且3529252115401530⨯+⨯=>，1529352111701150⨯+⨯=>，满足；C ：共50节且3531251915601530⨯+⨯=>，1531351911301150⨯+⨯=<，不满足；D ：共50节且3530252015501530⨯+⨯=>，153035201150⨯+⨯=，满足；故选：C.【变式6-1】（22-23高一上·山东·月考）某化工厂制定明年某产品的生产计划，受下面条件的制约：生产每袋需用4h ；生产此产品的工人不超过200人，每个工人的年工作时间约为2100h ；生产每袋需用原料20kg ，年底库存原料600t ，明年可补充1200t ；此产品今年销售量是60000袋，预计明年的销售量至少在今年的基础上增长13．根据这些数据条件可以预测明年的产量在（ ）A ．70000到75000袋之间B ．70000到80000袋之间C ．80000到85000袋之间D ．80000到90000袋之间【答案】D【解析】设明年的产量为x 袋，则()42002100160000132060012001000x x x ⎧≤⨯⎪⎪⎛⎫≥+⎨ ⎪⎝⎭⎪⎪≤+⨯⎩，所以8000090000x ££，故可以预测明年的产量在80000到90000袋之间，故选：D.【变式6-2】（23-24高一上·全国·专题练习）王老师是高三的班主任，为了更好地督促班上的学生完成作业，王老师特地组建了一个学习小组的钉钉群，群的成员由学生、家长、老师共同组成．已知该钉钉群中男学生人数多于女学生人数，女学生人数多于家长人数，家长人数多于教师人数，教师人数的两倍多于男学生人数．则该钉钉群人数的最小值为（ ）A ．18B ．20C ．22D ．28【答案】C【解析】依题意，设教师、家长、女生、男生人数分别为,,,x y z t ，且,,,N x y z t *∈，于是1,12,123y x z y x t z y x ≥+≥+≥+≥+≥+≥+，则46x y z t x +++≥+，又23x t x >≥+，解得3x >，因此min 4x =，此时22x y z t +++≥，所以当4,5,6,7x y z t ====时，min ()22x y z t +++=，即该钉钉群人数的最小值为22.故选：C【变式6-3】（23-24高一上·吉林长春·月考）不等关系是数学中一种最基本的数关系，生活中随处可见.例如.已知b 克糖水中含有a 克糖(0)b a >>，再添加m 克糖(0)m >(假设全部溶解)，糖水变甜了.(1)请将这一事实表示为一个不等式.并证明这个不等式成立：(2)利用（1）中的结论证明：若,,a b c 为三角形的三边长，则2a b cb c a c a b++<+++.【答案】(1)a a mb b m+<+，(0,0)b a m >>>，证明见解析；(2)证明见解析；【解析】（1）糖水变甜了得出不等式a a mb b m+<+，(0,0)b a m >>>.证明：()()()aa ma b m b a m b b m b b m ++-+-==++()()()ab am ba bm m a b b b m b b m +---=++.0,0,0b a a b b >>∴-<> .0,0m b m >∴+> ，()0()m a b b b m -∴<+，a a mb b m+∴<+.（2）设ABC 的三边长分别为,,a b c ，则有,,a b c a c b b c a +>+>+>，由（1）已证不等式可得：c c c a b a b c +<+++，a a a b c a b c +<+++，b b ba c ab c+<+++，将以上不等式左右两边分别相加得：2c a b c c a a b b a b b c a c a b c a b c a b c+++++<++=+++++++++，所以，2c a b a b b c c a++<+++.一、单选题1．（22-23高一上·河北邢台·月考）在开山工程爆破时，已知导火索燃烧的速度是每秒0.5厘米，人跑开的速度为每秒4米，距离爆破点150米以外（含150米）为安全区．为了使导火索燃尽时人能够跑到安全区，导火索的长度x （单位：厘米）应满足的不等式为（ ）A ．41500.5x⨯<B ．41500.5x⨯≥C ．41500.5x⨯≤D ．41500.5x⨯>【答案】B【解析】由题意知导火索的长度x （单位：厘米），故导火索燃烧的时间为0.5x秒，人在此时间内跑的路程为40.5x ⎛⎫⨯ ⎪⎝⎭米，由题意可得41500.5x ⨯≥.故选：B.2．（23-24高一上·云南昆明·期中）设2254M a a =++，(1)(3)N a a =++，则M 与N 的大小关系为（ ）A ．M N >B ．M N=C ．M N<D ．无法确定【答案】A【解析】因为()()()22213254131024M N a a a a a a a ⎛⎫-=++-++=++=++> ⎪⎝⎭，所以M N >.故选：A.3．（23-24高一上·广东深圳·期末）已知,,R,a b c a b ∈>，则下列一定成立的是（ ）A ．11a b<B ．2ab b >C ．b c ba c a+>+D ．()()2211a c b c +>+【答案】D【解析】对于A ，当1,2a b ==-，则11a b>，故A 不正确；对于B ，当0b =时，由a b >可得20ab b ==，故B 不正确；对于C ，当2,1,0a b c ===时，b c ba c a+=+，故C 不正确；对于D ，因为210c +>恒成立，所以由a b >可得()()2211a c b c +>+，故D 正确.故选：D.4．（23-24高一上·安徽宣城·自主招生）已知实数a ，b ，则下列选项中正确的是（ ）A ．若a b >，则22a b >B ．若a b >，则22a b >C ．若a b >，则22a b >D ．若a b >，则11a b<【答案】C【解析】对于A 选项，1,1a b ==-，满足a b >，此时221,1a b ==，不满足22a b >，故A 错误；对于B 选项，1,1a b ==-，满足a b >，此时221,1a b ==，不满足22a b >，故B错误；对于C 选项，0a b >≥，所以222a b b >=，故C 正确；对于D 选项，1,1a b ==-，满足a b >，此时,1111a b==-，不满足11a b <，故D错误，故选：C.5．（23-24高一上·河南驻马店·期末）已知15,31a b -<<-<<，则以下错误的是（ ）A ．155ab -<<B ．46a b -<+<C ．28a b -<-<D ．553ab-<<【答案】D【解析】因为1,153a b -<<-<<，所以13b -<-<，对于A ，1515330a ab b -<<⎧⇒-<<⎨-<<⎩，1500a ab b -<<⎧⇒=⎨=⎩,151501a ab b -<<⎧⇒-<<⎨<<⎩,综上可得155ab -<<，故A 正确；对于B ，314156a b --=-<+<+=，故B 正确；对于C ，112358a b --=-<-<+=，故C 正确；对于D ，当14,2a b ==时，8a b=，故D 错误；故选：D.6．（23-24高一上·山东菏泽·月考）已知11x y -≤+≤，13x y ≤-≤，则32x y -的取值范围是（ ）A ．2328x y ≤-≤B ．3328x y ≤-≤C ．2327x y ≤-≤D ．53210x y ≤-≤【答案】A【解析】设()()()()32x y m x y n x y m n x m n y -=+--=-++，所以32m n m n -=⎧⎨+=-⎩，解得1252m n ⎧=⎪⎪⎨⎪=-⎪⎩，即可得()()153222x y x y x y -=++-，因为11x y -≤+≤，13x y ≤-≤，所以2≤()()153222x y x y x y -=++-8≤，故选：A ．二、多选题7．（23-24高一上·山东日照·期末）若实数a ，b ，c 满足()0a b b >≠且0a >，0c >，则下列不等式正确的是（ ）A ．11a b <B ．ac bc-<-C ．b c ba c a +>+D ．22222b a a b+>【答案】BC【解析】对于A ，若1,1a b ==-，则1111a b=>=-，所以A 错误，对于B ，因为a b >，所以a b -<-，因为0c >，所以ac bc -<-，所以B 正确，对于C ，因为a b >，0a >，0c >，所以()0c a b ->，()0a a c +>，所以()()()0()()b c b a b c b a c c a b a c a a a c a a c ++-+--==>+++，所以b c ba c a+>+，所以C 正确，对于D ，若1,1a b ==-，则2222112b a a b+=+=，所以D 错误，故选：BC8．（23-24高一上·四川乐山·期中）下列不等式中，一定成立的是（ ）A ．若0,a b c >>∈R ，则22c ca b<B ．若0,a b c >>∈R ，则22ac bc >C ．若0a b <<，则22a ab b >>D ．若0a b <<，则22a a b b+<+【答案】AC【解析】对于A ，由0a b >>，20c>，知110a b <<，得22c ca b<，故A 正确；对于B ，当0c =时，故B 错误；对于C ，当0a b <<时，由()20a ab a a b -=->，得2a ab >，又()20ab b b a b -=->，则2ab b >，故有22a ab b >>，故C 正确；对于D ，当2a =-，1b =-时，22a a b b +>+，D 中不等式不一定成立，故D 错误．故选：AC.三、填空题9．（23-24高一上·广东韶关·月考）已知x ∈R ，则23x + 2x .（填“<”，“>”，或“=”）【答案】>【解析】()2232120x x x +-=-+>，故232x x +>.故答案为：>.10．（23-24高一上·北京西城·期中）已知a ，b ，c 为实数，能说明“若a b c >>，则2a bc >”为假命题的一组a ，b ，c 的值是.【答案】1a =，1b =-，2c =-(答案不唯一)【解析】当1,1,2a b c ==-=-时，21a =，2bc =，此时满足a b c >>，但是2a bc <.故答案为：1,1,2a b c ==-=-(答案不唯一).11．（23-24高一上·山东菏泽·期中）“双节”遇上亚运会，民宿成为潮流趋势．民宿的改造中，窗户面积与地板面积之比越大，采光效果越好．现有一所地板面积为180平方米的民宿需要同时增加窗户和地板的面积，已知地板增加的面积是窗户增加的面积的2倍，且民宿改造后的采光效果不逊于改造前，则改造前的窗户面积最大为 平方米．【答案】90【解析】设改造前的窗户面积为x ，窗户增加的面积为y ，0,0x y >>，依题意1801802x x yy+≤+，即1802180180,2180,90x xy x y xy y x +≤+≤≤，所以改造前的窗户面积最大为90平方米.故答案为：90四、解答题12．（23-24高一上·福建泉州·月考）（1）已知R a ∈，设()21M a a =+，()()21N a a =+-，比较M 与N 的大小；（2）证明：已知a b c >>，且0a b c ++=，求证：c ca cb c>--.【答案】（1）M N >；（2）证明见解析.【解析】（1）()()()221721212()024M a a a a N a a a ++-=++==+--+>，则M N >；（2）因为a b c >>，且0a b c ++=，则0,0a c ><，则0a c b c ->->，则()()0a c b c -->，则10()()a cbc >--，则11()()0()()()()a c b c a c b c a c b c ⋅->⋅->----，则110b c a c>>--，又0c <则c c a c b c>--.命题得证.13．（23-24高一上·湖北·期中）（1）已知b 克糖水中含有a 克糖（0b a >>），再添加m 克糖。