任意拉格朗日-欧拉描述法研究进展
- 格式:pdf
- 大小:295.48 KB
- 文档页数:12

任意拉格朗日-欧拉描述的薄平板大幅扭转振动气动特性研究【摘要】本研究利用拉格朗日-欧拉描述,建立了薄平板大幅扭转振动的气动特性模型。
通过对模型进行分析和参数研究,揭示了薄平板振动在空气中的复杂行为。
数值模拟和实验验证结果表明,振动幅度和频率对气动性能有重要影响。
研究结果对于了解薄平板在风力作用下的振动特性具有重要意义。
结论部分总结了本研究的主要成果,并提出了未来进一步研究的方向。
本研究为深入探究薄平板振动气动特性提供了一定参考,有助于设计更稳定和高效的平板结构。
【关键词】拉格朗日-欧拉描述、薄平板、大幅扭转振动、气动特性、理论基础、模型建立、参数研究、数值模拟、实验验证、研究结论、进一步研究展望1. 引言1.1 研究背景在工程实践中,薄平板大幅扭转振动是一种常见的现象,例如飞机机翼在飞行过程中的扭转振动。
这种振动会对结构的气动特性产生影响,进而影响飞行性能和安全。
对薄平板大幅扭转振动的气动特性进行研究具有重要的理论和应用价值。
较早前的研究主要基于传统的欧拉描述,即假设流体为连续介质,沿着固体表面流动速度与固体表面速度一致,采用固体力学的方法研究振动结构的气动特性。
这种描述方法存在一定局限性,特别是在描述非定常流动时的精度不足。
为了更准确地描述薄平板大幅扭转振动的气动特性,拉格朗日-欧拉描述成为研究的焦点。
该描述方法考虑了流体的粒子运动轨迹,更适用于复杂的非定常流动情况。
通过拉格朗日-欧拉描述的研究,可以更深入地理解薄平板大幅扭转振动的气动特性,为优化结构设计和提高飞行性能提供理论支持。
1.2 研究意义薄平板大幅扭转振动是一种常见的气动力学现象,对于机械工程、航空航天领域具有重要的研究意义。
研究这一现象可以帮助我们更深入地了解气动特性对结构振动的影响,有助于改善飞行器、桥梁等结构的设计和性能优化。
通过对薄平板大幅扭转振动进行研究,可以为降低结构振动噪音提供重要的理论基础,有助于改善机械设备的安全性和舒适性。


任意拉格朗日欧拉法有限元法
拉格朗日欧拉法有限元法是数学中非常重要的两个方法,这种
方法在很多科学领域都有重要应用,比如正求解物理方程的有限元分
析中、分析根据拉格朗日原理和欧拉原理中相对部分的真空和介质光
速变化方案的光学方法中。
下面将进一步介绍它们的详细内容。
拉格朗日原理利用的是广义坐标和动力学方程来描述一个系统在
它运动过程中的方式。
当一个系统的作用力和位移满足拉格朗日原理时,我们可以用欧拉-拉格朗日方程求出系统运动规律。
它的一个重要
应用是在机械系统中,例如机械臂、摆杆等。
在这些系统中,我们可
以通过这个方法识别它们的运动方式,这个方法被广泛的应用于机械
工程中,可以在设计机械的过程中起到重要的作用。
欧拉原理描述的是在任意元素中的弹性材料应变变化的规律性。
通过欧拉原理和方程我们可以得出一个完整的材料应力和变化的方式。
欧拉原理的一个典型应用在于材料学和力学中,可以描述在极其高压
条件下的金属和塑料材料产生的应变和弹簧常数等。
另一方面,有限元法在物理学和工程技术中非常常用,主要用于
分析复杂问题中的边界问题,比如房间的隔音,桥梁的设计。
这种技
术以小组件为单位,实际模拟整个结构系统,通过计算每个小组件与
其他小组件的相互作用,最终得到整个结构的性能。
总的来说,拉格朗日欧拉法和有限元法是数学和物理领域两个非
常重要的方法,他们在不同科学领域都有非常广泛的应用,为设计和
研究提供了重要的方法和手段,他们都是建立在强大的数学原理之上的。

任意拉格朗日-欧拉描述的薄平板大幅扭转振动气动特性研究薄平板是一种在气动力学中常见的结构,它在空气中运动时会受到气动力的影响。
当薄平板发生大幅度扭转振动时,其气动特性会发生明显变化,这一现象在许多工程领域中都具有重要的理论和实际意义。
本文将使用拉格朗日-欧拉描述来研究薄平板大幅扭转振动的气动特性。
1. 引言薄平板是一种常见的结构,在飞行器、建筑结构等领域都有着广泛的应用。
当薄平板受到外部扰动时,会产生振动响应,而这种振动会受到空气的影响,产生气动力。
特别是在飞行器等高速运动的系统中,薄平板的气动特性对系统的稳定性和性能有着重要的影响。
研究薄平板大幅度扭转振动的气动特性具有重要的科学和工程意义。
2. 拉格朗日-欧拉描述拉格朗日-欧拉描述是描述流体运动的常用方法之一,它可以描述流体中各个质点的运动状态,包括位移、速度和加速度。
在研究薄平板的大幅度扭转振动时,可以使用拉格朗日-欧拉描述来建立动力学方程,从而分析平板受到的气动力和振动响应。
通过建立合适的数学模型,可以研究薄平板在不同气动参数和振动幅度下的气动特性,为工程设计和实际应用提供理论依据。
3. 薄平板大幅扭转振动的数学模型在研究薄平板大幅扭转振动的气动特性时,首先需要建立数学模型来描述平板的动力学特性。
考虑到薄平板的扭转振动,可以将平板分割成许多小片,每一小片都受到空气的作用力,根据牛顿第二定律建立小片的动力学方程。
还需要考虑平板的扭转刚度和气动力矩之间的关系,建立整体的动力学方程。
通过对平板受力的分析,可以得到平板的振动特性和气动特性,为后续的研究和分析提供基础。
4. 薄平板大幅扭转振动的气动特性分析在建立了数学模型之后,可以对薄平板大幅扭转振动的气动特性进行分析。
通过数值计算和理论分析,可以得到平板在不同气动参数和振动幅度下的气动力和振动响应。
特别是在平板发生气动失稳时,可以研究失稳机理和临界条件,为避免失稳提供理论支持。
还可以分析气动参数对振动响应的影响,为工程设计提供指导,优化平板的结构和运动参数。

应用欧拉-拉格朗日方法分析动脉粥样硬化性颈动脉血流的流-固相互作用Majid SIAVASHI;Ava BINA;Mojtaba SAYADNEJAD;Borhan BEIGZADEH【期刊名称】《Journal of Central South University》【年(卷),期】2024(31)1【摘要】本研究旨在模拟不同狭窄程度和脉搏率的颈动脉搏动血流。
采用流-固耦合(FSI)和任意拉格朗日-欧拉(ALE)方法研究了不同狭窄程度、脉搏率和动脉壁性质对周围流体的影响。
分别应用Carreau-Yasuda非牛顿超弹性模型和修正Mooney-Rivin超弹性模型于具有非牛顿行为的血液和超弹性血管壁。
结果得到血液的壁面径向位移、压力分布、轴向速度分布和壁面剪切应力。
通过增加狭窄的严重程度,轴向速度、血压变化、最大壁面剪切应力和壁面径向位移均呈增长趋势。
当脉率在狭窄程度为75%时,最大流量矩、壁面径向位移、压力、轴向速度和壁面剪应力的最大值均增大。
此外,与弹性和刚性模型相比,将动脉壁视为超弹性模型,将其周围流体视为非牛顿和非定常,可以使模拟更加真实。
在严重程度高达50%的狭窄中,红细胞受到轻微损害,而在严重程度为75%的狭窄中观察到溶血。
通过改善动脉粥样硬化,弹性模量从500 k Pa提高到2 MPa,在60 bpm脉率和狭窄程度75%下,剪切应力最大值增长65%。
与刚性和弹性动脉壁相比,动脉壁的超弹性模型导致较低的轴向速度、较低的血压、较低的剪切应力和较高的径向位移。
【总页数】18页(P151-168)【作者】Majid SIAVASHI;Ava BINA;Mojtaba SAYADNEJAD;Borhan BEIGZADEH【作者单位】Applied Multi-Phase Fluid Dynamics Lab. of Mechanical Engineering University of Science and Technology;Biomechatronics and Cognitive Engineering Research Lab. of Mechanical Engineering University of Science and Technology【正文语种】中文【中图分类】R54【相关文献】1.基于欧拉—拉格朗日方法的囊式贮箱流固耦合晃动问题的有限元仿真研究2.稠密气固两相流欧拉-拉格朗日法的研究现状3.阵性泥石流运动与堆积的欧拉-拉格朗日模型──Ⅱ.应用4.采用拉格朗日法与欧拉法模拟旋风筒内气固两相流的对比研究5.基于任意拉格朗日-欧拉流固耦合方法的标枪飞行仿真因版权原因,仅展示原文概要,查看原文内容请购买。


暨两岸船舶与海洋工程水动力学研讨会文集拉格朗日、欧拉和任意拉格朗日-欧拉描述的有限元分析孙江龙1杨文玉2 杨侠3(1 华中科技大学船舶与海洋工程学院,武汉 430074;2 华中科技大学机械科学与工程学院,武汉 430074;3 武汉工程大学机电工程学院,武汉 430073)摘要:对拉格朗日、欧拉和任意拉格朗日–欧拉三种描述方法进行了分析,为了便于理解给出了三种描述的参考构形和参考坐标系,在参考坐标系下根据物质导数的定义分别得到相应的速度和加速度,并进行比较,将三种描述方法的区别列于表中,清晰地阐述了三种描述之间的相互关系,并进行了有限元分析。
关键词:拉格朗日;欧拉;任意拉格朗日–欧拉;有限元法1 引言自由液面大晃动引起的强非线性往往给问题的求解造成很大困难,对大晃动问题进行数值模拟,要先解决描述方法的选择问题。
过去通常采用欧拉法[1-3]和拉格朗日法[4-5]来描述非定常自由面流体流动,它们有着各自的优势和局限性。
采用固定网格的欧拉描述,整个计算过程中计算网格始终保持初始状态,从而可以描述流体质点运动的急剧变化,如碎波等现象。
欧拉描述虽然可以有效地分析整个流场内部的运动,但很难精确跟踪流体的自由液面,即很难给出准确的自由面形状和位置。
在拉格朗日描述中,网格结点与流体质点在整个运动过程中始终保持重合,流体质点与网格结点之间不存在相对运动,因此很容易跟踪自由液面,适用于线性小晃动问题。
这不仅大大地简化了控制方程地求解,而且还能有效地跟踪流体质点的运动轨迹,准确地描述波动的自由液面。
但是,在涉及求解带自由面流体大幅运动时,此时的晃动已经具有很强的非线性特征,如果还采用拉格朗日描述,由于流体质点运动的急剧变化,将导致计算网格的扭曲,会面临网格奇异问题,从而使计算无法继续进行。
拉格朗日描述和欧拉描述虽有各自的优点,但也存在较大的缺陷,如果将它们有机地结合在一起,充分利用各自的优点并克服其缺点,则可以解决各自都难于解决的问题,任意拉格朗日–欧拉描述[6-7](ALE)方法就是基于该思路提出的。

任意拉格朗日欧拉方法拉格朗日欧拉方法(Lagrange-Euler method)是数学中的一种重要的微积分方法。
它被广泛应用于物理学、工程学、控制论、经济学等学科中,用于求解一类特殊的微分方程。
任意拉格朗日欧拉方法(Arbitrary Lagrange-Euler method)是拉格朗日欧拉方法的一种扩展,它可以用于求解更为复杂的微分方程,也可以处理更为复杂的分析问题。
在本文中,我们将介绍这种方法的基本原理,并通过一个实例来展示它的应用。
第一步:构建能量函数任意拉格朗日欧拉方法的第一步是构建能量函数(Energy function)。
能量函数是一个与系统状态变量相关的函数,通常用于描述系统中的物理特性。
根据能量守恒定律,能量函数在系统运动中保持不变,因此我们可以将它作为分析系统的基础。
以一个自由落体为例,我们可以用如下的公式来表示它的能量函数:$E = mgz + \frac{1}{2}mv^2$其中,m代表物体的质量,g代表重力加速度,z表示物体的高度,v表示物体的速度。
这个式子的意义是,物体在不受任何力作用的情况下,它的能量等于动能加势能。
在这个例子中,势能是由物体在高度z 处所受的重力引起的,动能则是由物体的速度所贡献的。
第二步:构建拉格朗日方程任意拉格朗日欧拉方法的第二步是构建拉格朗日方程(Lagrange equation)。
拉格朗日方程是用于描述系统运动的方程,它可以从能量函数中推导出来。
在我们的例子中,拉格朗日方程可以表示为:$\frac{d}{dt}\frac{\partial L}{\partial \dot{z}} -\frac{\partial L}{\partial z} = 0$其中,L表示拉格朗日函数(Lagrangian function),它可以从能量函数中通过如下方式推导得到:$L = \frac{1}{2}mv^2 - mgz$这个式子的意义是,拉格朗日函数代表着系统的运动状态,它是由动能与势能之间的差值所确定的。

欧拉方法和拉格朗日方法欧拉方法是一种简单的近似方法,用于求解常微分方程的初值问题。
它基于一个重要的数值近似原理,即在一个小区间上,如果函数的导数变化不太大,那么可以将函数的变化等同于导数的变化。
具体来说,欧拉方法将原始的微分方程转化为离散的差分方程,并根据初始条件逐步逼近问题的解。
对于一个一阶常微分方程dy/dx = f(x, y),欧拉方法将自变量x和因变量y分成若干个小区间,每个小区间的长度为h。
利用微分方程的性质,我们可以将函数在每个小区间上进行线性近似。
具体来说,我们从初始点(x0, y0)出发,根据微分方程的定义,计算出斜率k1=f(x0, y0),然后根据该斜率近似得到在下个小区间上的函数值y1=y0 + k1 * h。
以此类推,我们可以得到在每个小区间上的近似函数值。
欧拉方法的一个明显局限是误差较大,特别是在相对大的步长h下。
这是因为欧拉方法只考虑了导数在小区间上的线性变化,忽略了更高阶的项,导致近似解与真实解的误差随着步长的增加而累积。
拉格朗日方法是一种改进的近似方法,用于求解微分方程的数值解。
它基于拉格朗日插值多项式的思想,通过将微分方程中的函数y(x)近似为一个多项式函数来逼近实际解。
具体而言,拉格朗日方法通过利用初始点(x0,y0)的函数值和导数值,在每个小区间上构造一个插值多项式L(x),该多项式是一个关于x的n次多项式,其中n是方程的阶数。
在拉格朗日方法中,我们首先确定每个小区间的节点,例如选取三个节点x0,x1,x2,并计算出这些节点上的函数值y0,y1,y2、然后我们利用这些节点构造一个三次拉格朗日插值多项式L(x),具体形式为:L(x)=L0(x)*y0+L1(x)*y1+L2(x)*y2,其中L0(x),L1(x),L2(x)是三个插值基函数。
通过这个多项式L(x),我们可以逐步计算出每个小区间上的函数值,并不断迭代得到近似解。
与欧拉方法相比,拉格朗日方法考虑了更高阶的项,在相对大的步长下,其近似解与真实解的误差更小。
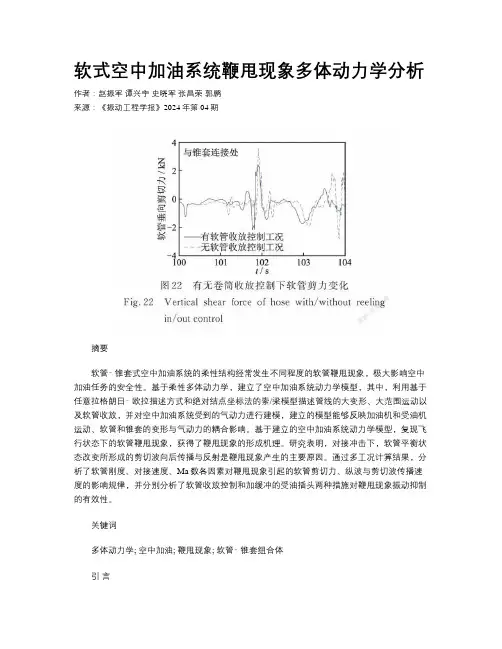
软式空中加油系统鞭甩现象多体动力学分析作者:赵振军谭兴宇史晓军张昌荣郭鹏来源:《振动工程学报》2024年第04期摘要软管‑锥套式空中加油系统的柔性结构经常发生不同程度的软管鞭甩现象,极大影响空中加油任务的安全性。
基于柔性多体动力学,建立了空中加油系统动力学模型,其中,利用基于任意拉格朗日‑欧拉描述方式和绝对结点坐标法的索/梁模型描述管线的大变形、大范围运动以及软管收放,并对空中加油系统受到的气动力进行建模,建立的模型能够反映加油机和受油机运动、软管和锥套的变形与气动力的耦合影响。
基于建立的空中加油系统动力学模型,复现飞行状态下的软管鞭甩现象,获得了鞭甩现象的形成机理。
研究表明,对接冲击下,软管平衡状态改变所形成的剪切波向后传播与反射是鞭甩现象产生的主要原因。
通过多工况计算结果,分析了软管刚度、对接速度、Ma数各因素对鞭甩现象引起的软管剪切力、纵波与剪切波传播速度的影响规律,并分别分析了软管收放控制和加缓冲的受油插头两种措施对鞭甩现象振动抑制的有效性。
关键词多体动力学; 空中加油; 鞭甩现象; 软管‑锥套组合体引言空中加油是飞行器在不着陆情况下,实现燃油快速补给、提升战机滞空时间、及时投入战场作战的主要技术手段。
根据加油管路方案的不同,空中加油可以分为软管式加油和硬管式加油两种方式[1],中国主要采用软管式加油方式。
软管是一根长达数十米的柔性体,在对接过程中受到多种内外部干扰因素影响,比如加油对接操纵方式、软管柔性材料、飞行Ma数、加油机尾流、姿态变化、受油机头波等[2]。
软管鞭甩现象是造成空中加油失败的主要原因之一[3],在空中加油的对接和输油阶段,受油机高速对接引起软管松弛,有可能发生软管鞭甩现象,轻则导致加油行动失败,重则使受油机受损、危及飞行安全。
因此,深刻揭示软管鞭甩现象的内在机理,提出有效的抑制/解决措施,对于提高空中加油的安全性、可靠性具有十分重要的意义。
对空中加油管线系统动力学建模方法主要有两种:多刚体动力学链式模型、有限元梁/索模型。

流体运动描述方法(欧拉法和拉格朗日法) -CAL-FENGHAI.-(YICAI)-Company One1在流体力学里,有两种描述流体运动的方法:欧拉(Euler)和拉格朗日(Lagrange)方法。
欧拉法描述的是任何时刻流场中各种变量的分布,而拉格朗日法却是去追踪每个粒子从某一时刻起的运动轨迹。
在一个风和日丽的午后,YC坐在河岸边看河水流,恩,她总是很闲。
如果YC 的位置不动,她在自己目光能及的河面上划出一块区域,数某一时刻经过的船只数,如果可能的话,再数数经过的鱼儿数;当然,如果手头有些仪器,她可以干干正事,比如测测水流的速度、水的压力、水的温度等,由此得到每一时刻这一河流区域水流各物理量的分布。
那么YC是在用欧拉方法研究流体。
这时,YC忽然看到一条船上坐着她的初恋情人,虽然根据陈安对初恋情人的定义,YC根本没有初恋情人。
现在假设她有,天哪,他们有20年没见面了,他还欠她20元呢,不能放了他。
于是YC记下第一眼看到初恋情人的时间,并迅速测出此时船的位置和速度,然后撒腿追去。
假设这条船是顺水而下,船的速度即是水流的速度。
每隔一个时间点,她便测一下船的速度和位置。
为了曾经的爱情,还有那不计利息的20元,她越过山岗,淌过小溪,直到那条船离开了她的视线。
于是,她得到了这条船在河流中的运动轨迹。
YC此时所用的研究方法就是拉格朗日法。
Understood而在一些复杂的两相流动问题里,比如粒子在流场中运动的问题,我们关注的是粒子的运动轨迹,因此,我们可以用拉格朗日方法追踪粒子在流场中的运动,同时,用欧拉方法来计算流场的各物理量。
在许多工程领域,都有纤维在流场中运动的问题。
如果将纤维在流场中的运动视为两相流动,必须为纤维作一些改变,因为它不同于一般的刚性粒子。
它细长,细长到你无法用一个粒子来代表一根纤维;它柔,柔得自己的每一部分可以相对于其他部分发生变形。
我在《柔性纤维的妖娆运动》里,为slender and flexible纤维建立了模型,把纤维离散成一个个粒子,并在粒子之间建立了弹性或粘弹性的连接。
§1.2 描述流体运动的方法
二、欧拉方法和随体导数
1、欧拉方法
•着眼于流场——流动空间。
描述任意时刻流动空间中各物理量的分布。
•将物理量表示为空间位置和时间的函数。
场点位置坐标称为欧拉变数。
e.g.,速度场:直角坐标系下:•定常流动&非定常流动
•其他物理量场:•两种方法比较:前者便于追踪,后者便于数学处理(场论)
(,)
V V r t =
(,,,)V V x y z t =
(,)(,)(,)a a r t r t p p r t ρρ===
,,等
例1.2 圆桶内流体绕轴线以等角速旋转,
(1)以欧拉方法表述流体运动的速度和加速度;(2)以拉格朗日方法表述流体质点的运动方程、速度和加速度;
解:选取柱坐标系。
1)V r r e θωω=⨯= ,2a r ω=-
2)运动方程:000
, , r r t z z θθω==+=其中()000, , r z θ为质点初始坐标。
非定长流动轨迹
4、其它相关概念
1)脉线(条纹线):不同时刻经过同一给定场点的流体质点的
连线。
2)流面和流管:在流场中取一段曲线(或一条闭合曲线), 经过其上各点的流线组成流面(或
流管)。
* 瞬时性
* 流线不能与流面相交或穿出、
穿入流管
例如:水管
3)时间线。
流体力学拉格朗日法和欧拉法转换
从拉格朗日法到欧拉法:流体力学的数学描述
流体力学是研究流体运动的学科,它涉及到许多物理现象,如流体的运动、压力、密度等。
为了描述这些现象,数学家们提出了两种不同的数学描述方法:拉格朗日法和欧拉法。
拉格朗日法是以流体中的每个质点为基础,描述流体的运动。
在拉格朗日法中,我们将流体中的每个质点看作一个独立的实体,它们的位置和速度随时间而变化。
因此,我们可以用质点的位置和速度来描述流体的运动状态。
这种方法的优点是可以很好地描述流体中的微观现象,但是对于大规模的流体运动,计算量会非常大。
欧拉法是以流体中的每个点为基础,描述流体的运动。
在欧拉法中,我们将流体看作一个连续的实体,它的位置和速度随时间而变化。
因此,我们可以用流体的密度、速度和压力来描述流体的运动状态。
这种方法的优点是可以很好地描述大规模的流体运动,但是对于微观现象的描述能力较弱。
为了将拉格朗日法转换为欧拉法,我们需要使用质点的速度和加速度来描述流体的速度和加速度。
这个过程称为拉格朗日-欧拉转换。
在这个过程中,我们需要使用一些数学工具,如雅可比矩阵和拉格朗日乘子法。
拉格朗日法和欧拉法是两种不同的数学描述方法,它们各有优缺点。
在实际应用中,我们需要根据具体情况选择合适的方法来描述流体的运动。
任意拉格朗日欧拉算法是一种数值分析方法,用于求解常微分方程初值问题。
该算法由拉格朗日和欧拉两种方法组合而成,兼具两者的优点。
拉格朗日方法从问题的初始状态出发,逐步逼近问题的解。
它通过构造一个能量函数来描述系统的物理特性,并利用能量守恒定律来分析系统的运动过程。
在拉格朗日方法中,我们需要构建拉格朗日方程,该方程描述了系统状态变量的变化规律。
欧拉方法则从问题的已知解出发,逐步逼近问题的解。
它通过构造一个加速度函数来描述系统的物理特性,并利用牛顿第二定律来分析系统的运动过程。
在欧拉方法中,我们需要构建欧拉方程,该方程描述了系统状态变量的变化规律。
任意拉格朗日欧拉算法则是将这两种方法结合起来,先利用拉格朗日方法求解出初始状态,再利用欧拉方法逐步逼近问题的解。
通过这种组合方式,任意拉格朗日欧拉算法可以更加高效地求解常微分方程初值问题。
在任意拉格朗日欧拉算法中,需要构建一个能量函数和一个加速度函数。
这两个函数通常需要依据具体的物理问题进行设计。
在实际应用中,可以根据具体问题的特点和要求,选择不同的
函数形式和参数设置,以达到最佳的求解效果。
描述流体运动(连续介质变形)的两种方法
拉格朗日法是以研究单个流体质点运动过程作为基础,综合所有质点的运动,构成整个流体的运动。
以某一起始时刻每个质点的坐标位置(a、b、c),作为该质点的标志。
任何时刻任意质点在空间的位置(x、y、z)都可以看成是(a、b、c)和t
的函数
拉格朗日法基本特点: 追踪流体质点的运动
优点: 可直接运用固体力学中质点动力学进行分析
在涉及几何非线性问题的有限单元法中,通常都采用增量分析方法,它基本上可以采用两种不同的表达格式。
第一种格式中所有静力学和运动学变量总是参考于初始位形,即在整个分析过程中参考位形保持不变,这种格式称为完全的Lagrange格式。
另一种格式中所有静力学和运动学的变量参考于每一载荷或时间步长开始时的位形即在分析过程中参考位形是不断被更新的,这种格式称为更新的Lagrange格式。
欧拉法是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法。
——流场法
它不直接追究质点的运动过程,而是以充满运动液体质点的空间——流场为对象。
研究各时刻质点在流场中的变化规律。
将个别流体质点运动过程置之不理,而固守于流场各空间点。
通过观察在流动空间中的每一个空间点上运动要素随时间的变化,把足够多的空间点综合起来而得出的整个流体的运动情况。
》》》》》》》》》》》》》》》》》》》
几何非线性问题塑性变形——拉格朗日法。
拉格朗日运动学法和欧拉法全文共四篇示例,供读者参考第一篇示例:拉格朗日运动学法和欧拉法是在物理学中常用的两种解决运动学问题的方法。
它们分别以法国数学家拉格朗日和瑞士数学家欧拉的名字命名,是经典力学中的两种重要技术方法。
首先来介绍一下拉格朗日运动学法。
拉格朗日运动学法是以拉格朗日力学为基础的一种运动学方法,它是一种基于能量的方法,用于描述系统的运动。
在拉格朗日力学中,系统的运动由广义坐标q和广义速度\dot{q}描述,其中q是系统的广义坐标,\dot{q}是广义坐标对时间的导数。
在使用拉格朗日运动学法求解物体的运动时,我们需要先写出系统的拉格朗日函数,通常用L表示。
拉格朗日函数是系统的动能T和势能V的差值,即L=T-V。
然后,我们可以得到系统的拉格朗日方程,即拉格朗日方程为\frac{d}{dt}(\frac{\partialL}{\partial\dot{q}})-\frac{\partial L}{\partial q}=0,其中\frac{\partial L}{\partial\dot{q}}表示拉格朗日函数对广义速度的偏导数。
通过求解拉格朗日方程,我们可以得到系统中每个物体的运动方程,并得到物体的轨迹。
拉格朗日运动学法不仅能够描述质点的运动,还可以描述刚体的运动,对于复杂系统的分析具有重要意义。
而欧拉法是一种基于牛顿第二定律的运动学方法。
在欧拉法中,我们将系统的运动描述为物体的加速度与外力之间的关系。
根据牛顿第二定律F=ma,我们可以得到物体的加速度a与外力F之间的关系。
在使用欧拉法解决物体的运动问题时,我们需要确定系统中每个物体的受力情况,并建立物体的受力平衡方程。
然后,我们可以根据牛顿第二定律得到物体的加速度a,并利用积分求解得到物体的速度和位移。
与拉格朗日运动学法相比,欧拉法更加直观和易于理解,适用于描述一些力学问题。
对于复杂系统的分析,欧拉法可能并不适用,因为系统中的受力很难确定。