流动的分类拉格朗日法和欧拉法质点导数迹线和流线、流
- 格式:ppt
- 大小:884.51 KB
- 文档页数:54

1.拉格朗日法:以研究个别流体质点的运动为基础,通过对每个流体质点运动规律的研究来获得整个流体运动的规律性2.欧拉法:以考察不同流体质点通过固定的空间点的运动情况来了解整个流体空间内的流动情况3.过流断面:在流束上作出的与流线正交的横断面4.流场:运动流体占据的空间5.恒定流:流体的各点运动要素不随时间变化非恒定流:流体上点的运动要素随时间改变6.当地加速度:由于时间过程而使空间上的质点速度发生变化的加速度迁移加速度:流动过程中质点由于位移占据不同的空间点而发生速度变化的加速度全加速度:流体质点速度随时间的变化率7.迹线:流体质点在某一时段的运动轨迹流线:某一时刻不同流体质点的速度方向8.流管:一非流线且不自交的封闭曲线,从封闭曲线上各个点绘出流线,组成封闭管状曲面流束:流管内的流体元流:过流断面面积无限小的流束总流:过流断面面积具有一定大小的有限尺寸的流束9.流量:单位时间内通过某一过流断面的流体数量(体积流量,重量流量,质量流量)10.均匀流:某一时刻,各点速度不随位置而变化的流体运动相应点速度相等的流体运动非均匀流:在某一时刻,各点速度随位置而变化相应点速度不相等的流体运动渐变流:所有流线是一组几乎平行的直线急变流:各流线之间夹角很大,或各流线的曲率半径很小11.有压流:边界全部为固体的流体运动无压流(明渠流):边界部分为固体,部分为大气射流:运动的流体脱离原来限制它的固体边界在充满流体的空间继续流动的流体运动12.三维流:流体的运动要素是空间三个坐标和时间t的函数的流体运动二维流:流体的运动要素是空间两个坐标和时间t的函数的流体运动一维流:流体的运动要素是空间一个坐标和时间t的函数的流体运动13.流体微元:由大量流体质点组成的具有线性尺度效应的微小流体团流体运动的形式:平移,变形(线变形,角变形),转动14.无涡流:每一流体微元的角转速为零,又称有势流速度势有涡流:每一流体微元的角转速不为零,流场中有角转速存在15.皮托管:测量流体点速度16.驻点:速度为零的点,驻点处流体的动能全部转化为压能17.平面势流18.水力坡度(能线坡度):单位长度上的水头损失19.总流伯努利方程的物理意义:总流各过流断面上单位重量流体所具有的势能平均值与动能平均值之和,即总机械能的平均值沿流程减少20.能量损失:沿程阻力和沿程损失,局部阻力和局部损失21.文丘里管:测量恒定有压管流的流量22.水泵扬程:单位重量的水流通过水泵后增加的能量水泵扬程=上下游水面高差+全部管路中的水头损失提水高度(扬水高度:上下游水面高差)23.断面平均流速:假设总流同一过流断面上各点的速度都相等,大小均为断面平均流速,以断面平均流速通过的流量等与该过流断面上各点实际速度不相等情况下所通过的流量。

流体力学欧拉法和拉格朗日法流体力学是研究流体运动规律的学科,它是物理学、数学和工程学的交叉学科。
在流体力学中,欧拉法和拉格朗日法是两种常用的描述流体运动的方法。
欧拉法是以欧拉方程为基础的一种描述流体运动的方法。
欧拉方程是描述流体运动的基本方程,它是由质量守恒、动量守恒和能量守恒三个基本方程组成的。
欧拉法的基本思想是将流体看作是一个连续的介质,通过对流体的宏观性质进行描述,如流体的密度、速度、压力等。
欧拉法适用于研究流体的宏观性质,如流体的流量、压力、速度等。
拉格朗日法是以拉格朗日方程为基础的一种描述流体运动的方法。
拉格朗日方程是描述流体运动的另一种基本方程,它是由质点的运动方程和流体的连续性方程组成的。
拉格朗日法的基本思想是将流体看作是由无数个质点组成的,通过对每个质点的运动进行描述,如质点的位置、速度、加速度等。
拉格朗日法适用于研究流体的微观性质,如流体的粘性、湍流等。
欧拉法和拉格朗日法各有优缺点,应用范围也不同。
欧拉法适用于研究流体的宏观性质,如流量、压力、速度等,但对于流体的微观性质,如粘性、湍流等,欧拉法的描述能力较弱。
而拉格朗日法适用于研究流体的微观性质,如粘性、湍流等,但对于流体的宏观性质,如流量、压力、速度等,拉格朗日法的描述能力较弱。
在实际应用中,欧拉法和拉格朗日法常常结合使用,以充分发挥它们各自的优势。
例如,在研究飞机的气动力学问题时,可以使用欧拉法来研究飞机的气动力学特性,如升力、阻力等;而在研究飞机的流场问题时,可以使用拉格朗日法来研究流体的微观性质,如湍流、涡旋等。
欧拉法和拉格朗日法是描述流体运动的两种基本方法,它们各有优缺点,应用范围也不同。
在实际应用中,需要根据具体问题选择合适的方法,以充分发挥它们的优势。








流体运动描述方法(欧拉法和拉格朗日法) -CAL-FENGHAI.-(YICAI)-Company One1在流体力学里,有两种描述流体运动的方法:欧拉(Euler)和拉格朗日(Lagrange)方法。
欧拉法描述的是任何时刻流场中各种变量的分布,而拉格朗日法却是去追踪每个粒子从某一时刻起的运动轨迹。
在一个风和日丽的午后,YC坐在河岸边看河水流,恩,她总是很闲。
如果YC 的位置不动,她在自己目光能及的河面上划出一块区域,数某一时刻经过的船只数,如果可能的话,再数数经过的鱼儿数;当然,如果手头有些仪器,她可以干干正事,比如测测水流的速度、水的压力、水的温度等,由此得到每一时刻这一河流区域水流各物理量的分布。
那么YC是在用欧拉方法研究流体。
这时,YC忽然看到一条船上坐着她的初恋情人,虽然根据陈安对初恋情人的定义,YC根本没有初恋情人。
现在假设她有,天哪,他们有20年没见面了,他还欠她20元呢,不能放了他。
于是YC记下第一眼看到初恋情人的时间,并迅速测出此时船的位置和速度,然后撒腿追去。
假设这条船是顺水而下,船的速度即是水流的速度。
每隔一个时间点,她便测一下船的速度和位置。
为了曾经的爱情,还有那不计利息的20元,她越过山岗,淌过小溪,直到那条船离开了她的视线。
于是,她得到了这条船在河流中的运动轨迹。
YC此时所用的研究方法就是拉格朗日法。
Understood而在一些复杂的两相流动问题里,比如粒子在流场中运动的问题,我们关注的是粒子的运动轨迹,因此,我们可以用拉格朗日方法追踪粒子在流场中的运动,同时,用欧拉方法来计算流场的各物理量。
在许多工程领域,都有纤维在流场中运动的问题。
如果将纤维在流场中的运动视为两相流动,必须为纤维作一些改变,因为它不同于一般的刚性粒子。
它细长,细长到你无法用一个粒子来代表一根纤维;它柔,柔得自己的每一部分可以相对于其他部分发生变形。
我在《柔性纤维的妖娆运动》里,为slender and flexible纤维建立了模型,把纤维离散成一个个粒子,并在粒子之间建立了弹性或粘弹性的连接。
第二章 流体运动学§2.1描述流体运动的两种方法一、拉格朗日法(Lagrange methord )从流体质点为研究对象研究流体运动的一种方法。
也叫质点系法。
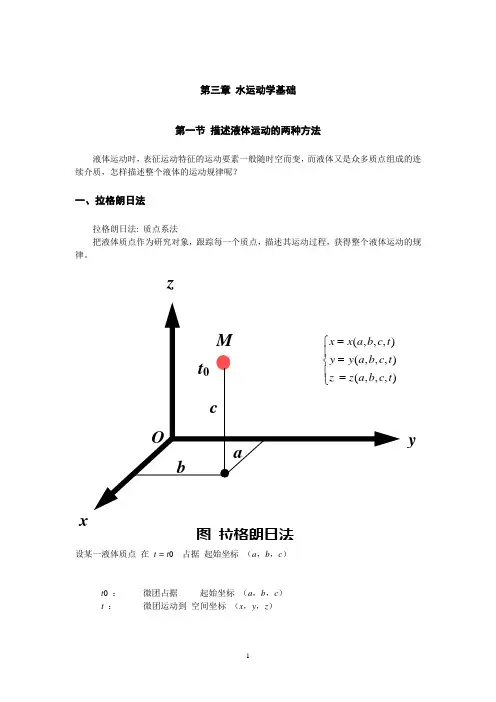
在拉格朗日法中,流体质点的运动轨迹的方程可表示为:⎪⎩⎪⎨⎧===),,,(),,,(),,,(t c b a z z t c b a y y t c b a x x (2—1)式中x,y,z 为流体质点的轨迹座标值。
a,b,c 称为拉格朗日变量,是流体质点的标识符,不同的流体质点a,b,c 的值不同t 为时间变量。
式(2—1),当a,b,c 为一组常数时t 为变数时,表示某个确定的流体质点随时间t 运动的运动轨迹座标值轨迹线。
当t 为固定值,a,b,c 为一组变数时,表示该组质点在某一固定时刻所处的位置(即空间位置的座标值)。
流体质点的轨迹也可用向径表示:),,,(t c b a r k z j y i x r =++= 对于某个确定的流体质点,其速度向量V 可用向径随时间的变化率表示:dt dF V =对于不同质点的流体质点,a,b,c 为变数所以速度向量应表示为r 对时间的偏导数形式:),,,(t c b a V tr V =∂∂= 在直角正交坐标系中速度向量的表达为:k w j v i u V ++=其中 t x u ∂∂=,t y v ∂∂=,tz w ∂∂= 质点的加速度:),,,(22t c b a a tF t V a =∂∂=∂∂= k a j a i a a z y x ++=22t x t u a x ∂∂=∂∂=,22t y t v a y ∂∂=∂∂=,22t z t w a z ∂∂=∂∂= 同样,其它流体质点的物理量也均可表示成为拉格朗日变数的函数:密度:),,,(t c b a ρρ=压力:),,,(t c b a p p =温度:),,,(t c b a T T =一般情况下所有的流体质点的物理量均可表示成:),,,(t c b a B B =B 可以是标量,如T p ,,ρ,也可以是矢量如a V r ,,可统一称为流体质点的物理量。
流体力学欧拉法和拉格朗日法
流体力学中常用的求解流体运动的数学方法有欧拉法和拉格朗日法。
欧拉法是以欧拉方程为基础的数值计算方法,该方程描述了流体在欧拉坐标系下的运动。
欧拉法侧重于研究流体的宏观特性,如速度场和压力场等,是求解高速流动和流体冲击现象的一种有效方法。
拉格朗日法则是以拉格朗日方程为基础的数值计算方法,该方程描述了流体在质点坐标系下的运动。
拉格朗日法更适合描述流体的微观性质,如涡旋和流体颗粒的轨迹等,在研究定常流动和流体混合等问题时具有广泛的应用。
欧拉法和拉格朗日法是流体力学中两种常用的数学方法,各有其优缺点,应根据具体问题的特性灵活选择。
流体力学中的流体流动的分析方法流体力学是研究流体运动和其它力学性质的学科。
在流体力学中,流体流动的分析方法起着至关重要的作用。
本文将介绍流体力学中常用的流体流动分析方法,包括拉格朗日法和欧拉法。
一、拉格朗日法拉格朗日法是一种基于微观粒子运动的流体流动分析方法。
它假设流体中的每个微观粒子都遵循牛顿力学定律,即受到外力和流体内部力的作用。
通过追踪每个微观粒子的运动轨迹,可以获得流体流动的具体信息。
在拉格朗日法中,流体流动可以用流体粒子的速度场来描述。
速度场是指在每个点上流体粒子的速度向量。
通过对速度场进行数值模拟或实验测量,可以得到流体的速度分布情况。
此外,拉格朗日法还可以用于研究流体流动中的湍流和运动物体的流动等问题。
二、欧拉法欧拉法是一种基于宏观流体性质的流体流动分析方法。
它假设流体是连续的,并且在每个点上都存在局部的物理量,如密度、压力和速度等。
通过对这些物理量的空间分布进行建模,并结合质量守恒、动量守恒和能量守恒等基本方程,可以得到流体的整体性质和流动规律。
在欧拉法中,流体流动可以用宏观流量进行描述。
流量是指通过某个横截面的流体质量或体积的时间变化率。
通过对流量进行数值计算或实验测量,可以获得流体的流量分布情况。
欧拉法广泛应用于研究流体流动的宏观特性,如流体的压力分布、流速分布以及流体的输运性质等。
综上所述,流体力学中的流体流动分析方法主要有拉格朗日法和欧拉法。
拉格朗日法通过追踪流体粒子的运动轨迹,研究流体流动的微观特性;欧拉法通过对流体的宏观性质进行建模,研究流体流动的宏观特性。
这两种方法在流体力学中都具有重要的应用价值,能够帮助我们深入理解流体流动的本质和规律。
但需要注意的是,拉格朗日法和欧拉法都是近似的理论模型,在实际应用中会受到一些假设和限制条件的影响。
因此,在具体问题的研究中,我们需要根据实际情况选择合适的方法,并结合数值模拟和实验数据进行验证和修正,以获得更精确的流体流动分析结果。