导入_图形的中心对称-优质公开课-青岛8下精品
- 格式:ppt
- 大小:1.76 MB
- 文档页数:8


初中数学青岛版八年级下册高效课堂资料11.3 图形的中心对称(2)主备人:周晓蒙参备人:周晓蒙赵祥庆郝金磊刘素英杨树强时间:20170518【课标要求】了解中心对称、中心对称图形的概念,探索它的性质,会判断是否是中心对称图形并能找出中心对称图形的对称中心。
【教学目标】1.了解中心对称、中心对称图形的概念,了解中心对称的性质;2.能找出线段、平行四边形的对称中心.会画出与已知图形成中心对称的图形;3.通过本节的学习,引导学生体验几何美,提高学习兴趣;【教学重难点】重点:经历探索中心对称图形的有关概念及了解一些简单的几何图形的对称性;难点:中心对称图形与中心对称的关系,准确判断图形的对称性;【教学过程】一.新课导入:复习:l.什么叫中心对称?中心对称有什么性质?2.如图1,作出四边形关于点的对称图.图1【设计意图】通过复习前面的知识,让学生对本单元知识有了一定的把握,为本节课的知识做铺垫。
二.探究过程探究一:中心对称图形的概念定义:在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做中心对称图形.180后,它的两个端点互换了位置,旋例1 如图2(制成教具演示),线段绕它的中心旋转转后的线段和原线段重合,因此,线段是中心对称图形,线段的中点是它的对称中心.图2【设计意图】通过教具演示,让学生理解中心对称图形和对称中心。
探究二:平行四边形是中心对称图形吗?如果是找出对称中心。
如图3中的ABCD ,点O 是对角线的交点,因为OC OA =,OD OB =,所以图表绕点O 旋转180后,点A 与点C ,点B 与点D 分别互换了位置,旋转后的图形和原来的图形重合,因此平行四边形是中心对称图形,对角线的交点是它的对称中心.图3问:矩形,菱形,正方形是不是中心对称图?为什么?【设计意图】通过平行四边形、矩形、菱形、和正方形对称中心的找法,体会一般中心对称图形的对称中心找法,主要是根据定义找.探究三:中心对称和中心对称图形的区别与联系.区别:①中心对称是指两个全等图形之间的相互位置关系,这两个图形关于某一点(对称中心) 对称,叫做中心对称;中心对称图形是指一个图形本身成中心对称(对称中心含于图形本身). ②成中心对称的两个图形中,其中一个图形上的所有点关于对称中心的对称点都在另一个图形 上,反之亦然.中心对称图形上所有点关于对称中心的对称点都在这个图形的本身上. 联系:①如果针对中心对称的两个图形看成一个整体(一个图形)那么这个图形就是中心对称 图形.②一个中心对称图形,如把对称的部分看成两个图形,那么它们又是中心对称.【设计意图】通过回顾中心对称,让学生体会两者的区别和联系。

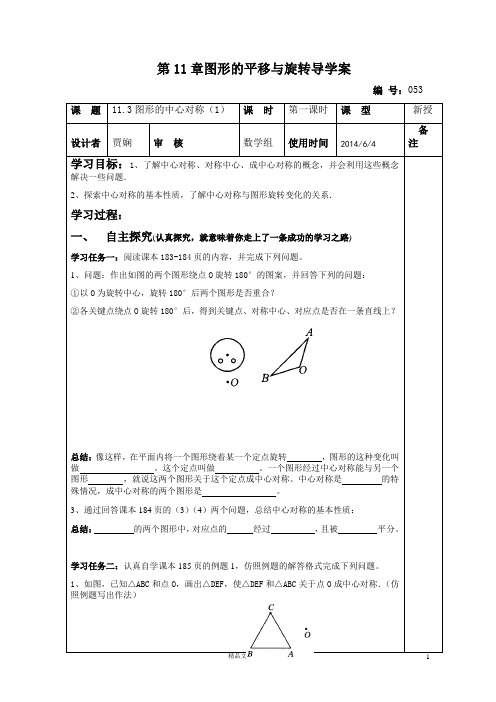
第11章图形的平移与旋转导学案编号:053课题11.3图形的中心对称(1)课时第一课时课型新授设计者贾娴审核数学组使用时间2014/6/4备注学习目标:1、了解中心对称、对称中心、成中心对称的概念,并会利用这些概念解决一些问题.2、探索中心对称的基本性质,了解中心对称与图形旋转变化的关系.学习过程:一、自主探究(认真探究,就意味着你走上了一条成功的学习之路)学习任务一:阅读课本183-184页的内容,并完成下列问题。
1、问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题:①以O为旋转中心,旋转180°后两个图形是否重合?②各关键点绕点O旋转180°后,得到关键点、对称中心、对应点是否在一条直线上?总结:像这样,在平面内将一个图形绕着某一个定点旋转,图形的这种变化叫做。
这个定点叫做。
一个图形经过中心对称能与另一个图形,就说这两个图形关于这个定点成中心对称。
中心对称是的特殊情况,成中心对称的两个图形是。
3、通过回答课本184页的(3)(4)两个问题,总结中心对称的基本性质:总结:的两个图形中,对应点的经过,且被平分。
学习任务二:认真自学课本185页的例题1,仿照例题的解答格式完成下列问题。
1、如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(仿照例题写出作法)巩固练习:1、如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD•成中心对称的三角形.(只保留作图痕迹,不要求写出作法)2、如图,已知两个四边形成中心对称,作出它们的对称中心。
二、交流展示温馨提示:同学们先在组内交流一下自主学习情况,然后在班内展示。
(要知道提出一个问题比解决一个问题更有价值!)三、拓展提升:1、在直角坐标系中,已知点A(3,0)、B(0,-2)、C(-2,3)、D(-3,2),分别作出她们关于原点O城中心对称的点,并写出对称点的坐标。
总结关于原点成中心对称的两个点的坐标有什么关系?2、如图,矩形ABCD和矩形关于点A中心对称.四边形是菱形吗?为什么?四、达标测评:(满分10分)(相信自己,我一定能行,我一定行)1、下列说法中,正确说法的个数是()①成中心对称的两个图形全等;②成中心对称的两个图形中,对应点的连线被对称轴平yxO。
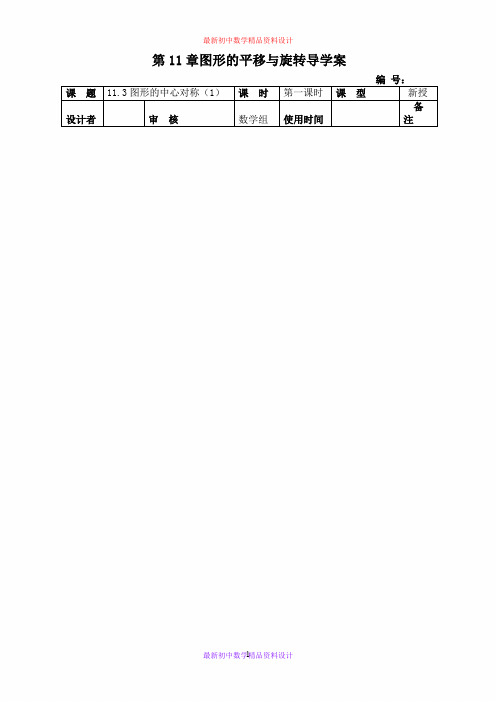
第11章图形的平移与旋转导学案编号:课题11.3图形的中心对称(1)课时第一课时课型新授设计者审核数学组使用时间备注最新初中数学精品资料设计1学习目标:1、了解中心对称、对称中心、成中心对称的概念,并会利用这些概念解决一些问题.2、探索中心对称的基本性质,了解中心对称与图形旋转变化的关系.学习过程:一、自主探究(认真探究,就意味着你走上了一条成功的学习之路)学习任务一:阅读课本183-184页的内容,并完成下列问题。
1、问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题:①以O为旋转中心,旋转180°后两个图形是否重合?②各关键点绕点O旋转180°后,得到关键点、对称中心、对应点是否在一条直线上?总结:像这样,在平面内将一个图形绕着某一个定点旋转,图形的这种变化叫做。
这个定点叫做。
一个图形经过中心对称能与另一个图形,就说这两个图形关于这个定点成中心对称。
中心对称是的特殊情况,成中心对称的两个图形是。
3、通过回答课本184页的(3)(4)两个问题,总结中心对称的基本性质:总结:的两个图形中,对应点的经过,且被平分。
学习任务二:认真自学课本185页的例题1,仿照例题的解答格式完成下列问题。
1、如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(仿照例题写出作法)巩固练习:1、如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD•成中心对称的三角形.(只保留作图痕迹,不要求写出作法)2、如图,已知两个四边形成中心对称,作出它们的对称中心。
二、交流展示温馨提示:同学们先在组内交流一下自主学习情况,然后在班内展示。
(要知道提出一个问题比解决一个问题更有价值!)三、拓展提升:yx O最新初中数学精品资料设计2最新初中数学精品资料设计3 1、在直角坐标系中,已知点A (3,0)、B (0,-2)、C (-2,3)、D (-3,2),分别作出她们关于原点O 城中心对称的点,并写出对称点的坐标。

青岛版八下数学11.3图形的中心对称说课稿一. 教材分析青岛版八下数学11.3图形的中心对称,是在学生已经掌握了中心对称图形的概念,以及对称轴、对称中心等基本知识的基础上进行讲解的。
本节内容主要让学生了解中心对称图形的性质,以及如何运用中心对称图形解决实际问题。
教材通过丰富的图片和实例,激发学生的学习兴趣,引导学生探索中心对称图形的性质,从而提高学生的空间想象能力和思维能力。
二. 学情分析学生在学习本节内容前,已经掌握了基本的几何知识,对中心对称图形有了初步的认识。
但部分学生对中心对称图形的性质和运用可能还不够熟练,需要老师在教学中给予引导和启发。
此外,学生对实际问题的解决能力有待提高,需要老师通过实例进行讲解和训练。
三. 说教学目标1.知识与技能:让学生掌握中心对称图形的性质,学会运用中心对称图形解决实际问题。
2.过程与方法:通过观察、操作、探索等活动,培养学生的空间想象能力和思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生勇于探索、积极思考的精神。
四. 说教学重难点1.教学重点:中心对称图形的性质及其运用。
2.教学难点:如何引导学生探索中心对称图形的性质,以及如何运用中心对称图形解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、实例教学法、合作学习法等。
2.教学手段:利用多媒体课件、几何画板等辅助教学。
六. 说教学过程1.导入:通过展示一些生活中的中心对称图形,如天安门、蝴蝶等,引导学生回顾中心对称图形的概念,激发学生的学习兴趣。
2.新课讲解:讲解中心对称图形的性质,如对称轴、对称中心等,并通过实例进行说明。
3.课堂互动:让学生分组讨论,探索中心对称图形的性质,老师巡回指导,解答学生的疑问。
4.巩固练习:布置一些有关中心对称图形的练习题,让学生独立完成,老师及时批改和讲解。
5.实际问题解决:通过一些实际问题,让学生运用中心对称图形进行分析和解决,提高学生的应用能力。
第十一章第8课时 11.3图形的中心对称(2) 总第67课时【学习目标】1、知道中心对称图形的概念。
2、能判断一个图形是不是中心对称图形。
【学习重点】中心对称图形的概念。
【学习难点】能判断一个图形是不是中心对称图形,并利用其特点解决问题。
一、课前预习:(认真预习,就意味着你走上了一条成功的学习之路) 学习任务一:学习课本186页“观察与思考”的内容,理解中心对称图形的概念。
1、如图,在平面内,将△ABC 绕点O 旋转180°,它与△A /B /C /重合。
像这样,在平面内,中心对称图形。
2、指出上图的对称中心 ,对称点 。
点D ,E 的对称点分别是点D /,E /,连接DD /,EE /,发现都经过 ,且 = , = 3、如图,线段AB 与CD 交于点O ,且OA=OB ,OC=OD 。
ΔAOC 与ΔBOD 成中心对称吗?如果把ΔAOC 与ΔBOD 看做是一个图形,那么这个图形是中心对称图形吗?思考:中心对称图形与成中心对称图形的区别学习任务二:阅读课本187页的例2,仿照例题格式完成下列问题。
1、如图,ABCD 是一块平行四边形的土地,请你把这块土地分成面积相等的四部分。
你有哪些不同的方案?画出图形,并说明理由。
预习检测:1、下列图形其中中心对称图形有 。
(1)线段 (2)角 (3)正三角形 (4)平行四边形 (5)菱形 (6)矩形 (7)正方形 (8)等腰梯形 2、中心对称图形与轴对称图形的区别与联系.BCDA预习质疑:(要知道提出一个问题比解决一个问题更有价值!)三拓展提升:1、如图,在△ABC 中,AB=AC ,△ABC 与△FEC 关于点C 成中心对称。
连接AE 、BF. ⑴线段AE 与BF 有怎样的位置关系和大小关系?说明理由。
⑵如果△ABC 的面积为3cm 2,求四边形ABFE 的面积; ⑶当∠ACB 为多少度时,四边形ABFE 为矩形?说明理由。
三、系统总结:(总结可以使你不断提高)判断中心对称图形的方法是: 四、达标测评:(满分10分)(相信自己,我一定能行,我一定行) 1、下列图案中是中心对称图形的是( )2、(2分)在等边三角形、正方形、矩形、菱形中,是轴对称图形但不是中心对称图形的是3、下图中,轴对称图形有: ;中心对称图形有:CFE BA4、如图,从一副扑克牌中抽出如下四张牌,其中是中心对称图形的有()5、在等腰直角三角形ABC中,∠C=90°,BC=4,以边AC的中点P为中心,作出与△ABC 成中心对称的△AB/C,则BB/的长为。