剪力图和弯矩图4(例题)
- 格式:ppt
- 大小:415.00 KB
- 文档页数:16
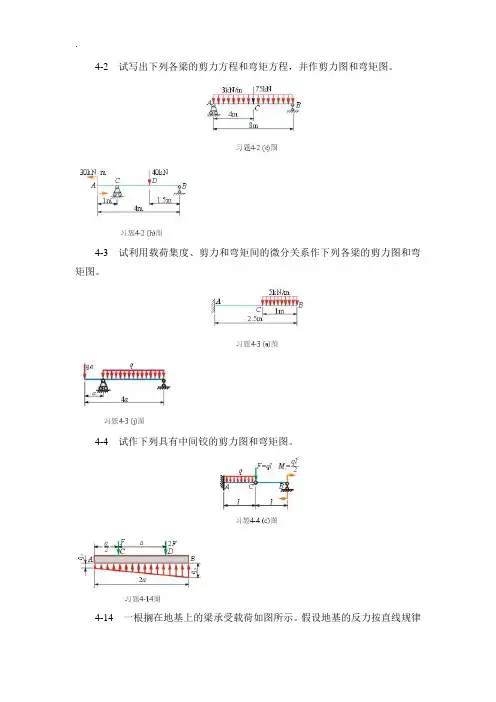
4-2 试写出下列各梁的剪力方程和弯矩方程,并作剪力图和弯矩图。
4-3 试利用载荷集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。
4-4 试作下列具有中间铰的剪力图和弯矩图。
4-14 一根搁在地基上的梁承受载荷如图所示。
假设地基的反力按直线规律
连续变化。
试求反力在两端A点和B点处的集度q A和q B,并作梁的剪力图和弯矩图。
4-15 试作图示刚架的剪力图、弯矩图和轴力图。
4-22 厚度为h=1.5mm的钢带,卷成直径为D=3m的圆环,试求钢带横截面上的最大正应力。
已知钢的弹性模量E=210GPa。
4-25 矩形截面的悬臂梁受集中力和集中力力偶作用,如图所示。
试求截面m-m和固定端截面n-n上A、B、C、D四点处的正应力。
4-32 简支梁的荷载情况及尺寸如图所示,试求梁的下边缘的总伸长。
4-39 一矩形截面简支梁由圆柱形木料锯成。
已知F =5kN ,a =1.5m ,[σ]=10MPa 。
试确定弯曲截面系数为最大时矩形截面的高宽比h /b ,以及梁所需木料的最小直径d 。
4-48 一矩形截面木梁,其截面尺寸及载荷如图,q =1.3kN/m 。
已知[σ]=10MPa ,[τ]=2MPa 。
试校核梁的正应力和切应力强度。
4-52 图示木梁受一可移动的载荷F =40kN 作用。
已知[σ]=10MPa ,[τ]=
3MPa 。
木梁的横截面为矩形,其高宽比23=b h 。
试选择梁的截面尺寸。




悬臂梁的剪力图和弯矩图如下:内力规律图如下1当剪力图与x轴平行时,弯矩图在空载区是倾斜的。
当剪力图为正时,弯矩图向下倾斜。
当剪切图为负时,弯矩图向上倾斜。
均布荷载的规律是:荷载向下,剪力向下,凹弯矩向上。
三。
当施加集中力时,剪切图突然变化,突变的绝对值等于集中力的大小,弯矩图旋转。
4集中联轴器动作时,转矩图发生突变,突变的绝对值等于集中联轴器的耦合转矩。
剪切图像没有更改。
5在零剪力作用下,存在一个弯矩极值弯矩图汇总规则如下:1在梁的某一截面上,如果没有分布荷载,即Q(x)=0,则D?看。
M(x)/DX?2=q(x)=0,其中m(x)是x的函数,弯矩图是对角线。
2在梁的某一截面上,如果施加分布荷载,即Q(x)=常数,则d≥d.2m(x)/DX?2=q(x)=常数可以得出m(x)是x的二次函数,力矩图是抛物线。
三。
如果在梁的某个部分fs(x)=DM(x)/DX=0,则该部分的弯矩存在极值(最大值或最小值)。
也就是说,弯矩的极值出现在剪力为零的截面上。
根据上述绘图规则,可准确绘制集中荷载和均布荷载作用下悬臂梁的剪力图和弯矩图。
扩展数据弯矩叠加原理相同的梁AB承受Q和M0荷载,只有Q和M0。
当Q和M0一起工作时,VA=QL/2+M0/L 和=QL/2+M0/L从计算结果可以看出,梁的反力和弯矩是荷载的一阶函数(Q,M0),即反力或弯矩与荷载呈线性关系。
在这种情况下,G和M0共同作用产生的反作用力或弯矩等于G 和M0单独作用产生的反作用力或弯矩的代数和。
这种关系不仅存在于本例中,也存在于其他机械计算中。
也就是说,只要反作用力、弯矩(或其他量)和荷载是线性的,则由多个荷载引起的反作用力和弯矩(或其他量)分别等于每个荷载的反作用力和弯矩(或其他量)。
这种关系叫做叠加原理。
应用叠加原理的前提是构件处于小变形状态,各荷载对构件的影响是独立的。
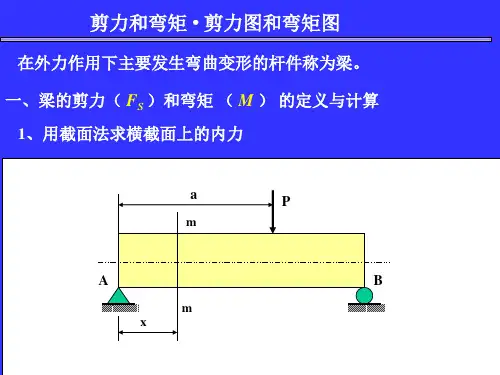

1.简支梁受力如图a 所示。
试写出梁的剪力方程和弯矩方程,并作剪力图和弯矩图。
解:(1)求支座反力由平衡方程∑=0B m 和∑=0A m 分别求得ql R A 83=,ql R B 81= 利用平衡方程∑=0y 对所求反力进行校核。
(2)建立剪力方程和弯矩方程以梁的左端为坐标原点,建立x 坐标,如图a 所示。
因在C 处分布载荷的集度发生变化,故分二段建立剪力方程和弯矩方程。
AC 段:qx ql x Q -=83)(1 )20(l x ≤< 212183)(qx qlx x M -= )20(l x ≤≤ CB 段: ql x Q 81)(2-= )2(l x l <≤ )(81)(2x l ql x M -= )2(l x l ≤≤ 3.求控制截面内力,绘Q 、M 图Q 图:AC 段内,剪力方程)(1x Q 是x 的一次函数,剪力图为斜直线,故求出两个端截面的剪力值,ql Q A 83=右,ql Q C 81-=左,分别以a 、c 标在x Q -坐标中,连接a 、c 的直线即为该段的剪力图。
CB 段内,剪力方程为常数,求出其中任一截面的内力值,例如ql Q B 81-=左,连一水平线即为该段剪力图。
梁AB 的剪力图如图b 所示。
M 图:AC 段内,弯矩方程)(1x M 是x 的二次函数,表明弯矩图为二次曲线,求出两个端截面的弯矩,0=A M ,2161ql M C =,分别以a 、c 标在x M -坐标中。
由剪力图知在d 点处0=Q ,该处弯矩取得极值。
令剪力方程0)(1=x Q ,解得l x 83=,求得211289)83(ql l M =,以d 点标在x M -坐标中。
据a 、d 、c 三点绘出该段的弯矩图。
CB 段内,弯矩方程)(2x M 是x 的一次函数,分别求出两个端点的弯矩,以c 、b 标在x M -坐标中,并连成直线。
AB 梁的M 图如图c 所示。
2.梁的受力如图a 示,利用微分关系作梁的Q 、M 图。



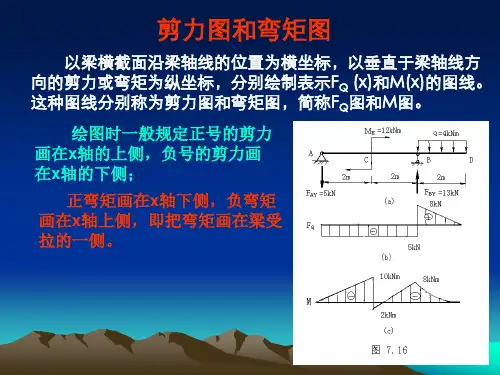
简支梁的剪力图和弯矩图例题
简支梁是一种受拉拔及弯矩影响的梁,它可以用来支撑荷载,改变楼层的结构形式,也可以用来支撑桥梁。
简支梁由梁顶、支点及梁端组成,其中梁顶受到拉拔和弯矩的双重作用,支点只受拉拔作用,梁端只受弯矩作用。
简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的,它们是构成简支梁的基本工程图象。
简支梁的剪力图是用来分析梁顶的剪力的,它是由梁顶的剪力构成的图象,从而求出梁顶的剪力状态。
一般来说,简支梁剪力图是由梁顶上拉拔力的大小及其方向构成的,它以梁顶为枢纽,把力划分为两部分,一部分是向上的拉力,另一部分是向下的拉力,这样就可以求出梁顶的剪力状态。
简支梁的弯矩图是用来分析梁顶的弯矩的,它是由梁顶的弯矩构成的图象,从而求出梁顶的弯矩状态。
一般来说,简支梁弯矩图也是由梁顶上弯矩的大小及其方向构成的,它以梁顶为枢纽,把弯矩划分为两部分,一部分是向上的弯矩,另一部分是向下的弯矩,这样就可以求出梁顶的弯矩状态。
简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的,它们是确定梁的设计参数的基础。
根据剪力图和弯矩图,可以确定梁顶的荷载状态,从而确定梁顶的设计参数,使梁能够满足设计要求。
因此,简支梁的剪力图和弯矩图非常重要,必须正确地计算和分析,以确保梁的安全性和结构稳定性。
总之,简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的,它们是构成简支梁的基本工程图象,是确定梁的设计参数的基础,是确保梁的安全性和结构稳定性的重要工具和手段。
正确的分析简支梁的剪力图和弯矩图,是确保梁的安全性和结构稳定性的关键,也是工程师们必须掌握的重要技能。