当前位置：文档之家 › 5.剪力和弯矩图习题

5.剪力和弯矩图习题

  • 格式：ppt
  • 大小：1.29 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

材料力学习题解答5

材料力学习题解答5
Fs F
M FR sin
F

T FR(1 cos )
R


F
R sin
R(1 cos )
9．如图所示，半径为 R 的四分之一个圆的曲梁一端固 定，一端自由，曲梁受垂直于轴线平面的载荷作用。 试求曲梁的剪力、扭矩以及弯矩函数。 解：


Fs q d s qR
d FN q2 q1 dx d FS 0 dx
dM ( q q2 ) h Fs 1 dx 2
d FS 0 dx
FS C FS (0) 0 C 0
9．如图所示，半径为 R 的四分之一个圆的曲梁一端固 定，一端自由，曲梁受垂直于轴线平面的载荷作用。 试求曲梁的剪力、扭矩以及弯矩函数。 解：
2 kN
Fs
2 kN

㊀
2 kN
x
1m
1m
2m
2 kN
M
2 kNm
7． 设梁的弯矩图如图所示，试作梁的剪力图和载荷图。
20 kNm 10 kNm
10 kN
Fs
10 kN
10 kN
M
10 kN m

x
㊀ ㊀
10 kN m
1m 1m 1m
10 kN m
40 kNm
40 kN
40 kN
Fs
qa2
2qa2
2qa
qa2
FN
Fs
M
6． 设梁的剪力图如图所示，试作梁的弯矩图 和载荷图。已知梁上无集中力偶作用。
4 kN 0.75 kN/ m
3 kN
Fs
2 kN
3 kN

㊀
2 kN

剪力弯矩练习题

剪力弯矩练习题

常见问题题1题型：计算题题目：试作图所示悬臂梁A B的剪力图和弯矩图。

【解】1、列剪力方程和弯矩方程取坐标原点与梁左端点A对应。

选取距梁左端点A为x的任一截面，如图(a)所示，以该截面左侧梁段上的外力，写该截面上的剪力和弯矩表达式，即可得到梁A B 的剪力方程和弯矩方程为上面两式后的括号内，表明方程适用范围。

由于截面A,B处有集中力作用，则其剪力为不定值，第一式的适用范围为。

由于截面B有集中力偶作用，则其弯矩也为不定值，第二式的适用范围为关于这个问题，待后面作进一步说明。

2、作剪力图和弯矩图剪力方程表明，梁各截面上的剪力都相等，因此剪力图应是一条平行于横轴的直线。

取直角坐标系x—，画出梁的剪力图为一水平直线。

因各横截面的剪力为负值，故画在横轴下面，如图（b）所示。

弯矩方程表明，弯矩M是x的一次函数，因此弯矩图应是一条倾斜直线。

可以确定其上两点，在x=0处，M=0；在x=L处（应理解为x略小于L处），M=P L。

取直角坐标系O x M，表示弯矩的纵坐标以向下为正，画出梁的弯矩图，如图（c）所示。

由图可见，最大弯矩发生在固定端B稍偏左的横截面上，其值为常见问题题2题型：计算题题目：试作图（a）所示简支梁A B的剪力图和弯矩图。

【解】1、求支座反力由梁的平衡方程，可求得支座A,B两处的反力为2、列剪力方程和弯矩方程取坐标原点与梁左端点A对应。

列出梁A B的剪力方程和弯矩方程为3、作剪力图和弯矩图剪力方程表明，剪力是x的一次函数，剪力图应是一条倾斜直线。

因此，只要确定其上两点，即可绘出该梁的剪力图。

在处（应理解为x略大于0）,；处（应理解为x略小于），。

画出梁的剪力图，如图(b)所示。

由剪力图可见，，该梁最大剪力发生在支座内侧的横截面上，其值为弯矩方程表明，弯矩M是x的二次函数，弯矩图应是一条抛物线。

因此，只要确定其上三个点，即可绘出该梁的弯矩图。

在处，M=0；在处，M=0；在处，。

画出弯矩图，如图6-12(c)所示。

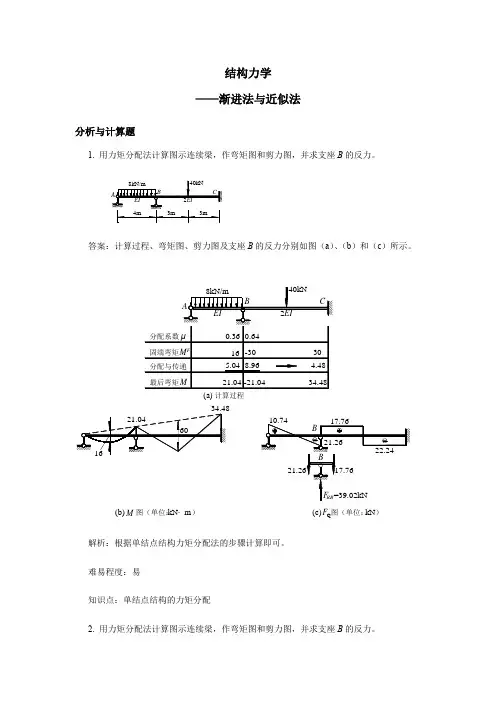
结构力学计算题经典(有答案)

结构力学计算题经典(有答案)

结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁，作弯矩图和剪力图，并求支座B 的反力。

答案：计算过程、弯矩图、剪力图及支座B 的反力分别如图（a ）、（b ）和（c ）所示。

解析：根据单结点结构力矩分配法的步骤计算即可。

难易程度：易知识点：单结点结构的力矩分配2. 用力矩分配法计算图示连续梁，作弯矩图和剪力图，并求支座B 的反力。

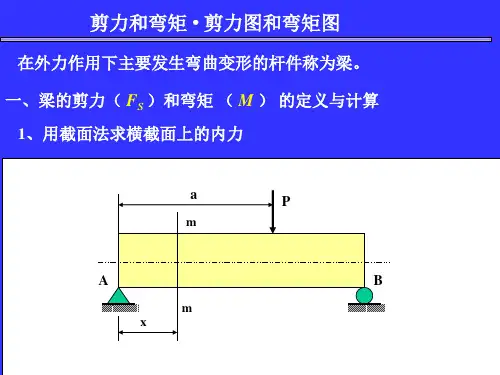
A60kN 40kN·m EIEI B C4m4m6m(b)M 图（单位： ）kN·m 图（单位： ）(c)kNQ F (a)计算过程答案：图（a ）为求解结点B 约束力矩的受力分析图。

计算过程、弯矩图、剪力图及支座B 的反力分别如图（b ）、（c ）和（d ）所示。

解析：根据单结点结构力矩分配法的步骤计算即可。

难易程度：中知识点：单结点结构的力矩分配3. 用力矩分配法计算图示连续梁，作弯矩图和剪力图，并求支座B 的反力。

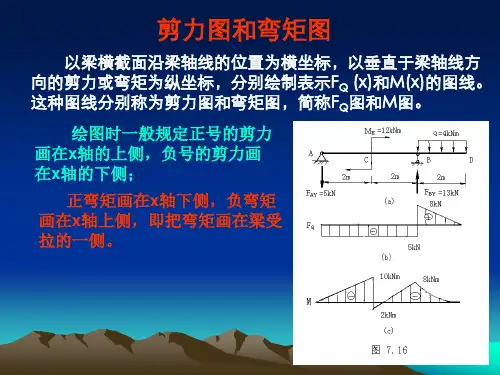
答案：CD 段为静定悬臂梁，将其截开并暴露出截面C 的弯矩，用力矩分配法计算如图（a ）所示结构。

弯矩图和剪力图如图（b ）、（c ）所示。

BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图（单位： ）(c)M kN·m图（单位： ）Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析：根据单结点结构力矩分配法的步骤计算即可。

本题中悬臂段CD 若不切除，则可按B 、C 两个刚结点的结构进行计算。

难易程度：中知识点：单结点结构的力矩分配4. 用力矩分配法计算图示连续梁，作弯矩图和剪力图，并求支座B 的反力。

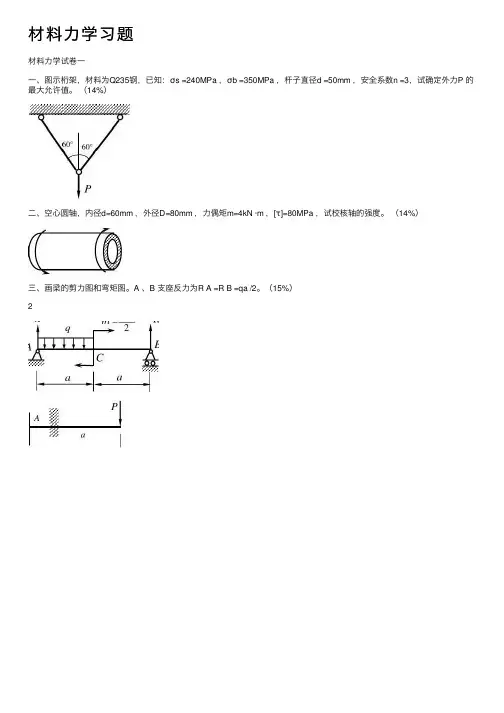
答案：AB 段为静定悬臂梁，将其截开并暴露出截面B 的弯矩，用力矩分配法计算过程如图（a ）所示。

弯矩图和剪力图图（b ）、（c ）所示。

kNQ F (c)图（单位： ）m M 图（单位： ）(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析：根据单结点结构力矩分配法的步骤计算即可。

剪力图和弯矩图

剪力图和弯矩图
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS(0) 0 FS(l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
绘剪力图和弯矩图的基本方法：首先分别写出梁 的剪力方程和弯矩方程，然后根据它们作图。
Fs(x)
o
x
o
x
Fs 图的坐标系
M(x) M 图的坐标系
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩，而向下 的外力则引起 负值 的弯矩。
例题：图示简支梁 ，在全梁上受集度为 q 的均布荷载作用。 试作此梁的剪力图和弯矩图。
FS 称为 剪力
y
FA
m
C
A
xm
FS x
由平衡方程
a
P
m
m C0
MFAx0
A
B
m
可得 M = FAx
x
内力偶 M 称为 弯矩
y
FA
m FS
C
x
A
xm
M
结论
a
P
m
梁在弯曲变形时，
横截面上的内力有
A
B
两个，即，
m x
剪力 FS 弯矩 M
y
FA
m FS
C
x
A
xm
M
取右段梁为研究对象。
y
FA
m FS
-
FS FS
dx
（2）弯矩符号 横截面上的弯矩使考虑的脱离体下边受拉，上边受压时为 正 。

工程力学(剪力与图)

工程力学(剪力与图)

2.弯矩图与荷载的关系 2.弯矩图与荷载的关系 (1)在均布荷载作用的区段， 图为抛物线。 (1)在均布荷载作用的区段，M图为抛物线。 在均布荷载作用的区段
d 2M(x) 图为上凹下凸。 (2)当q(x)朝下时 朝下时， (2)当q(x)朝下时， 2 = q(x) < 0 M图为上凹下凸。 dx 2 d M(x) q(x)朝上时 朝上时， 图为上凸下凹。 当q(x)朝上时， dx2 = q(x) > 0 M图为上凸下凹。
DB段:q<0, 段 剪力图为斜直线； 弯矩图为抛物线。
Q = Q = −P = −3kN
+ C − A
M C= 0 MA = −P ×a = −1.8kN
AD段:q=0, :q=0,剪力图为水平直线；
弯矩图为斜值线。
Q = −RB = −5kN Q(x) = −RB + qx (0 < x ≤ 2a)
AB段 AB段：
Me FQ ( x) = 0<x<l） l （0<x<l） AC段 AC段：
Me M ( x ) = F Ay x = x (0≤x≤a) l
CB段 CB段：
M ( x) = FAY x − Me = Me x − M e (a<x≤l) l
3.绘出剪力图和弯矩图 3.绘出剪力图和弯矩图
1 FAy = FBy = ql 2
2.列剪力方程和弯矩方程 2.列剪力方程和弯矩方程 1 FQ ( x) = FAy − qx = ql − qx 2
1 2 1 1 2 M ( x) = FAy x − 9 x = qlx − qx 2 2 2
3.作剪应力图和弯矩图 3.作剪应力图和弯矩图 最大剪力发生在梁端， 最大剪力发生在梁端，其值为

范钦珊版材料力学习题全解 第5章 梁的弯曲问题(1)-剪力图与弯矩图

范钦珊版材料力学习题全解 第5章 梁的弯曲问题(1)-剪力图与弯矩图

M A = ql 2
| FQ | max = 5 ql 4
| M | max = ql 2
题（c）
∑ F y = 0 ， FRA = ql （↑）
9
∑ M A = 0 ， M A = ql 2
∑ M D = 0 ， ql 2 + ql ⋅ l − ql ⋅ − M D = 0
3 2 ql 2 | FQ | max = ql MD =
C
4000 4000
B
FB
习题 5－8 载荷图之二
5－9 试作图示刚架的剪力图和弯矩图，并确定 FQ
max
、 M
max
12
习题 5－9 图
解：题（a） ：
∑M A = 0
FRB ⋅ 2l − FP ⋅ l − FP ⋅ l = 0
FRB = FP （↑）
∑ F y = 0 ， F Ay = FP （↓）
∑ Fx = 0 ， FAx = FP （←）
C
2
1
B
C
－
B
1
D
M(FPl)
1 +
D
FQ(FP)
A
A
习题 5－9a 的弯矩图
剪力图和弯矩图如图所示，其中 | M | max = 2 FP l ， 位于刚节点 C 截面；
| FQ |max = FP
题（b） ： ∑ F y = 0 ， F Ay = ql （↑）
8
习题 5－6c、e 解图
习题 5－6d、f 解图
题（b）
∑ M A = 0 − ql 2 − ql ⋅ l + ql ⋅ l + FRB ⋅ 2l = 0
2
FRB

材料力学习题

材料力学习题

材料⼒学习题材料⼒学试卷⼀⼀、图⽰桁架，材料为Q235钢，已知：σs =240MPa ，σb =350MPa ，杆⼦直径d =50mm ，安全系数n =3，试确定外⼒P 的最⼤允许值。

（14%）⼆、空⼼圆轴，内径d=60mm ，外径D=80mm ，⼒偶矩m=4kN ·m ，[τ]=80MPa ，试校核轴的强度。

（14%）三、画梁的剪⼒图和弯矩图。

A 、B ⽀座反⼒为R A =R B =qa /2。

（15%）2四、铸铁梁，截⾯惯性矩I Z=538cm4，y1=92mm，y2=42mm, P=5kN，l=2m,许⽤拉应⼒ [σt]=40MPa，许⽤压应⼒[σC]=90MPa，校核梁的弯曲正应⼒强度。

五、已知：载荷P，梁长a，梁的抗弯刚度为EI，试⽤积分法求梁的挠度⽅程，并求B 点挠度。

（14%）五、P=10kN，D=500mm，a=600mm，[σ]=90 MPa，试⽤第三强度理论设计B材料⼒学试卷⼆⼀、如图所⽰的圆截⾯杆，d =50mm ，在杆⼦的表⾯沿45°⽅向粘贴应变⽚，现测得应变ε=－400×10-6，材料常数E=210GPa ，µ=0.28，求外⼒偶矩m 的⼤⼩。

（20分）⼆、画剪⼒图和弯矩图。

已知⽀反⼒（22分）三、简⽀梁由两根No18号槽钢和上下盖板焊接⽽成，盖板材料与槽钢相同，σp =200MPa ，σs =235MPa ，σb =390MPa 。

盖板尺⼨为b =320mm ，t =16mm 。

已知P =140kN ，a =2m （。

, 2qa R qa R B A ==四、已知:杆⼦⾯积A =200 mm 2，长l =2m ，δ=1mm ，受外⼒P =60kN ，材料的弹性模量E =200GPa ，试画出杆⼦的轴⼒图。

（22分）五、钢制圆截⾯杆，直径d =80mm ， P=3kN ，m =4kN ·m ，a =1m ，试按第三强度理论，计算危险点的相当应⼒。

简支梁的剪力图和弯矩图例题

简支梁的剪力图和弯矩图例题

简支梁的剪力图和弯矩图例题
简支梁是一种受拉拔及弯矩影响的梁，它可以用来支撑荷载，改变楼层的结构形式，也可以用来支撑桥梁。

简支梁由梁顶、支点及梁端组成，其中梁顶受到拉拔和弯矩的双重作用，支点只受拉拔作用，梁端只受弯矩作用。

简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的，它们是构成简支梁的基本工程图象。

简支梁的剪力图是用来分析梁顶的剪力的，它是由梁顶的剪力构成的图象，从而求出梁顶的剪力状态。

一般来说，简支梁剪力图是由梁顶上拉拔力的大小及其方向构成的，它以梁顶为枢纽，把力划分为两部分，一部分是向上的拉力，另一部分是向下的拉力，这样就可以求出梁顶的剪力状态。

简支梁的弯矩图是用来分析梁顶的弯矩的，它是由梁顶的弯矩构成的图象，从而求出梁顶的弯矩状态。

一般来说，简支梁弯矩图也是由梁顶上弯矩的大小及其方向构成的，它以梁顶为枢纽，把弯矩划分为两部分，一部分是向上的弯矩，另一部分是向下的弯矩，这样就可以求出梁顶的弯矩状态。

简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的，它们是确定梁的设计参数的基础。

根据剪力图和弯矩图，可以确定梁顶的荷载状态，从而确定梁顶的设计参数，使梁能够满足设计要求。

因此，简支梁的剪力图和弯矩图非常重要，必须正确地计算和分析，以确保梁的安全性和结构稳定性。

总之，简支梁的剪力图和弯矩图是用来分析梁顶的剪力和弯矩的，它们是构成简支梁的基本工程图象，是确定梁的设计参数的基础，是确保梁的安全性和结构稳定性的重要工具和手段。

正确的分析简支梁的剪力图和弯矩图，是确保梁的安全性和结构稳定性的关键，也是工程师们必须掌握的重要技能。

剪力图和弯矩图4例题-弯矩图例题

剪力图和弯矩图4例题-弯矩图例题

02 在绘制剪力图时，需要将剪力值标在相应的位置 上，并使用箭头表示剪力的方向。
03 剪力图应与弯矩图一起绘制，以便更好地理解斜 梁的受力情况。
THANKS FOR WATCHING
感谢您的观看
简支梁的弯矩图绘制
根据简支梁的受力分析，可以确定跨 中截面和支座截面的弯矩值。
将确定的弯矩值按照比例绘制在相应 的位置上，连接各点即可得到弯矩图 。
简支梁的剪力图绘制
剪力图是表示剪力随截面位置变 化的图形。
根据简支梁的受力分析，可以确 定跨中截面和支座截面的剪力值。
将确定的剪力值按照比例绘制在 相应的位置上，连接各点即可得
剪力图和弯矩图4例题-弯矩图例 题 弯矩图例题二：悬臂梁 • 弯矩图例题三：连续梁 • 弯矩图例题四：斜梁
01 弯矩图例题一：简支梁
简支梁的受力分析
01
简支梁在均布载荷作用下，其跨 中截面只承受正弯矩，而支座截 面只承受负弯矩。
02
简支梁在集中载荷作用下，其跨 中截面和支座截面均承受弯矩， 但弯矩值不同。
到剪力图。
02 弯矩图例题二：悬臂梁
悬臂梁的受力分析
悬臂梁一端固定，另 一端自由，主要承受 垂直于梁轴线方向的 力。
悬臂梁的受力分析需 要考虑梁的长度、截 面尺寸、材料属性等 因素。
悬臂梁在自由端受到 集中力作用时，会产 生弯曲变形，并产生 弯矩。
悬臂梁的弯矩图绘制
根据受力分析，确定弯矩零点位置，通常在固定 端和自由端。
03
斜梁的剪力和弯矩随梁的长度和倾斜角度而变化。
斜梁的弯矩图绘制
根据斜梁的受力分析，可以确定弯矩的大小和 方向。
在绘制弯矩图时，需要将弯矩值标在相应的位 置上，并使用箭头表示弯矩的方向。

剪力方程和弯矩方程及剪力图和弯矩图

剪力方程和弯矩方程及剪力图和弯矩图

FS
(
x)
FRA
qx
ql 2
qx
(0 x l)
M(
x)
FRA
x
qx
x 2
qlx 2
qx2 2
(0 x l)
§5-4 剪力方程和弯矩方程 剪力图和弯矩图
q
FS
(
x)
ql 2
qx
(0 x l)
A
剪力图为一倾斜直线
x
FRA
l
x=0
处
， FS
ql 2
x= l 处 ,
FS
ql 2
ql/2
+
绘出剪力图
l
突变值等于集中力偶矩的数值.此处
M /l
剪力图没有变化.
+
Ma
+l
Mb l
§5-4 剪力方程和弯矩方程 剪力图和弯矩图
小结
1.取梁的左端点为坐标原点,x 轴向右为正:剪力图向上为正;弯矩 图向上为正. 2.以集中力、集中力偶作用处、分布荷载开始或结束处,及支座截 面处为界点将梁分段.分段写出剪力方程和弯矩方程,然后绘出剪 力图和弯矩图. 3.梁上集中力作用处左、右两侧横截面上,剪力（图）有突变,突 变值等于集中力的数值.在此处弯矩图则形成一个尖角.
§5-4 剪力方程和弯矩方程 剪力图和弯矩图
小结
4.梁上集中力偶作用处左、右两侧横截面上的弯矩（图） 有突变,其突变值等于集中力偶矩的数值.但在此处剪力图 没有变化.
5.梁上的FSmax发生在全梁或各梁段的边界截面处;梁上的Mmax发 生在全梁或各梁段的边界截面,或FS = 0 的截面处.
x
l
l
l
AC,CB 两梁段的弯矩图各是一条倾斜直线.

剪力弯矩练习题

剪力弯矩练习题

剪力弯矩练习题在结构分析和设计领域中，剪力和弯矩是两个重要的力学概念。

剪力指的是作用在结构上的垂直于截面的力，而弯矩则是由剪力引起的结构曲率。

掌握剪力和弯矩的计算方法和分析技巧对于工程师来说至关重要。

在这篇文章中，我们将通过练习题来巩固和加深对剪力和弯矩的理解。

练习问题1：直梁上的剪力和弯矩考虑一个简单的直梁结构，长度为L，均匀分布荷载为w。

我们将梁分为若干小段，每段的长度为Δx。

假设每段的载荷近似为常量，则每段的剪力V和弯矩M可通过以下公式计算：剪力V = -w * Δx弯矩M = w * Δx^2 / 2练习题1：现给定梁的长度L为10米，均匀分布荷载w为5 kN/m。

请你计算梁上各个位置的剪力和弯矩，并绘制剪力和弯矩图。

解答：首先，我们将梁分为若干小段，每段长度Δx为1米（为了简化计算，可以根据需要调整Δx的大小）。

在每个小段上，根据公式计算剪力和弯矩：位置x=0m：剪力V0 = -w * Δx = -5 kN/m * 1m = -5 kN弯矩M0 = w * Δx^2 / 2 = 5 kN/m * (1m)^2 / 2 = 2.5 kNm位置x=1m：剪力V1 = -w * Δx = -5 kN/m * 1m = -5 kN弯矩M1 = w * Δx^2 / 2 = 5 kN/m * (1m)^2 / 2 = 2.5 kNm位置x=2m：剪力V2 = -w * Δx = -5 kN/m * 1m = -5 kN弯矩M2 = w * Δx^2 / 2 = 5 kN/m * (1m)^2 / 2 = 2.5 kNm...以此类推，计算梁上不同位置的剪力和弯矩。

练习题2：点力和集中力的剪力和弯矩考虑一个简支梁，在梁的一端有一个向上的点力P作用。

我们需要计算在梁上不同位置的剪力和弯矩。

假设点力P作用的位置距离梁的左端为a，则剪力和弯矩的公式为：剪力V = -P弯矩M = -P * x练习题2：现给定点力P为10 kN，作用位置a为3米，梁的长度L为8米。

梁的剪力弯矩图习题解答

梁的剪力弯矩图习题解答

q
D B
b l
A
C
FA
a
c
FB
FA
FB
FAa
FBb
F
Fa
2k N m
a
F
a
5
4m
3kN
kN
kN
4
3
Fa
kNm
2.25
kNm
4kN m
6kN
2k N m
4.5
4.5
1m
1m
2m
5.5
kN 1.5
5.5
4
8.5 7
kNm
外伸梁AB承受荷载如图所示，作该梁的内力图。
6kN m
D B
解： 1、求支反力
剪力图和弯矩图 以梁横截面沿梁轴线的位置为横坐标，以垂直 于梁轴线方向的剪力或弯矩为纵坐标，分别绘 制表示V (x)和M(x)的图线。这种图线分别称为 剪力图和弯矩图，简称V图和M图。绘图时一 般规定正号的剪力画在x轴的上侧，负号的剪 力画在x轴的下侧；正弯矩画在x轴下侧，负弯 矩画在x轴上侧，即把弯矩画在梁受拉的一侧。
v
v v v v
v
v
v
v
利用上述规律： 1、可以检查剪力图和弯矩图是否正确。 2、可以快速的绘制剪力图和弯矩图，步骤如下： （1）将梁正确分段 （2）根据各段梁上的荷载情况，判断剪力图和弯矩图的 形状 （3）寻找控制面，算出各控制面的V和M （4）逐段绘制出V和M图即梁的V和M图
快速绘制剪力图和弯矩图
画剪力图和弯矩图时，一定要将梁正确分段， 分段建立方程，依方程而作图
例题1 简支梁受均布荷载作用，如图示， 作此梁的剪力图和弯矩图。
解：1.求约束反力 由对称关系，可得：

静定结构的内力—绘制剪力图和弯矩图(建筑力学)

静定结构的内力—绘制剪力图和弯矩图(建筑力学)

CB段：
Fs
x2
FBy
a l
F
a＜x2＜l
M
x2
FBy
l
x2

a l
F
l
x2
a x2 l
实作训练
（3）画剪力图和弯矩图
剪力图：FS 为常数，剪力图为平行于横坐标
轴的两段水平直线
弯矩图：
x1 0时，M A 0
x1
a时，MC
ab l
F
x2
a时，MC
ab l
F
x2 l时，MB 0
实作训练
弯矩图如图(c)所示。
例题:2：用列方程法作出图示梁的剪
力与弯矩图。
ql 解：由对称性可知，支座反力 FAy FBy 2
取距左端为x的任一横截面n-n，此横截面
的剪力方程和弯矩方程分别为
l Fs ( x) FAy qx q( 2 x)
(0 x l)
xq M ( x) FAy x qx 2 2 x(l x)
➢ 实作训练：
例题1：试列出图示梁的剪力方程与弯矩方程， 并作出剪力图与弯矩图。
解：（1）建立剪力方程和弯矩方程 以梁的左端为坐标原点，沿横截面n-n 将梁截开，取左段梁为分离体，应用求内力的直 接计算法得
FS x F 0＜x＜l a M x Fx 0 x l b
式（a）与（b）分别为剪力方程与弯矩方程。
x
F
x
l 3
3ql
2
4qlx
l/3 l
l/3 FBy
DB 段 FS x FAy F 4ql
M
x
FAy
x
F
x
l 3
Me
4ql 2

弯矩图练习题

弯矩图练习题

弯矩图练习题在力学中，弯矩图是一种图形表示方法，用于描述材料在受到外力作用下弯曲的情况。

通过解析力学的知识，我们可以根据给定的条件绘制出弯矩图，以帮助我们了解结构体在力的作用下的变形情况。

在本文中，我将介绍一些弯矩图的练习题，并解答它们。

1. 简支梁的考虑一个简支梁，其长度为L，受到均匀分布载荷q的作用。

为了绘制弯矩图，我们需要先计算出梁在各个点的剪力和弯矩。

首先，我们可以计算出梁的支反力。

由于梁是简支的，所以在两个端点的支反力大小相等。

根据平衡条件，我们可以得到：支反力R = qL/2接下来，我们可以计算出梁在任意位置x处的剪力V(x)和弯矩M(x)。

根据均布载荷的性质，我们可以得到：V(x) = R - qxM(x) = Rx - (q/2)x^2通过这些计算，我们可以绘制出梁的弯矩图。

在绘图时，我们将横轴表示位置x，纵轴表示弯矩M。

我们可以观察到，在简支梁上，弯矩图为一条抛物线形状，当x=L/2时，弯矩图达到最大值。

2. 悬臂梁的现在考虑一个悬臂梁，其长度为L，悬臂部分的长度为a。

该梁受到集中力F的作用。

对于悬臂梁，我们需要使用不同的方法来计算弯矩图。

首先，考虑梁的支反力。

由于悬臂梁只有一个支点，支反力大小与集中力F相等，方向相反。

支反力R = -F接下来，我们需要计算悬臂梁在不同位置x处的剪力V(x)和弯矩M(x)。

根据悬臂梁的几何特性和受力分析，我们可以得到：V(x) = -FM(x) = -Fx + Fx = 0从上述计算结果中可以看出，悬臂梁的弯矩图是一条直线，且弯矩始终为零。

这是因为在悬臂梁的支点处，不会出现弯矩。

3. 复杂结构的除了简支梁和悬臂梁，我们还可以考虑更加复杂的结构。

对于复杂结构，我们可以利用叠加原理来计算弯矩图。

以一个梁柱系统为例，梁的两端固定在墙上，悬臂部分受到集中力F的作用。

我们需要分别计算梁的弯矩图和柱的弯矩图，然后将它们叠加得到整个系统的弯矩图。

梁的弯矩图我们已经在第一题中计算过了，而柱的弯矩图可以通过悬臂梁的方法计算得到。

梁的剪力和弯矩概念讲解(剪力图弯矩图,含例题)

梁的剪力和弯矩概念讲解(剪力图弯矩图,含例题)
10kN m
X2
40 kN m
A
35kN
B
FS x1 20kN
M x1 20 x1
0 x1 1 0 x1 1
1m
15
4m
2.5
25kN
FS x2 25 10 x2
25
2 x2 M x2 25 x2 10 2
20
20
kN
0 x2 4
F=8kN
2、计算1-1
截面的内力 F A
3、计算2-2
FS1
q=12kN/m
M 1 F F F 7kN S1 A M1 FA 2 F (2 1.5) 26kN m
FS2 q 1.5 FB 11kN
FB
截面的内力
M2
FS2
M 2 FB 1.5 q 1.5
M ＞0
M＜0
剪力：使脱离体有顺时针转动趋势的剪力为正，反之为负； 弯矩：使脱离体产生向下凸变形的弯矩为正，反之为负。
6.2
例 题
试确定截面C及截面D上的剪力和弯矩
2 Fl
F
A
l
FCs
C
l
D
B
截面法求解
2 Fl
D
FCs F
C截面
F
B
M C Fl
FDs F
MC C
FDs
MD
D

l
F
B
D截面
2q1 x FA 2 x
x
l 2m a 0 .6 m
2 l a M C FA l a q
2
0
2q1 x 1.4 2 1.4 q 0 2 x 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题1
剪力、弯矩图习题
q
A
Fa
F
RA F
a
F
a
B
RB 0
Fs
M
Fa
习题2
q
A
剪力、弯矩图习题 q F qa
a
a
B
a
RB 2qa
C
RA qa
解：1）求支座反力
3a a M B 0 RA 2a qa 2 qa a qa 2 0 RA qa 5 a a M 0 A RB 2a qa qa a qa 0 2 2
上节课主要内容回顾：
微分关系 几何意义 剪力图上某点处切线的斜率等于 梁上该点处的分布载荷集度 q 弯矩图上某点处切线的斜率等于 梁上该点处截面上的剪力 Fs 弯矩图的凹凸方向取决于分布载 荷集度 q 的正负
d Fs ( x ) q( x ) dx
d M( x) Fs ( x ) dx
d M( x ) q( x ) 2 dx
RA
RB
解：1）求支座反力
3 qa 2 1 M B 0 RA a qa 2 a 2 qa 2 a 0 qa RA 2 2 a a qa M A 0 RB a qa qa 0 2 2 2 qa RB 2
习题4
0 弯矩为减函数，上斜直线
上节课主要内容回顾：
分布载荷、剪力图和弯矩图之间的规律
2.梁段上的分布载荷为不等于零的常数
dFs ( x ) (1) q( x ) 常数 0 dx
剪力为一次函数 剪力图为斜直线
0
q( x )
剪力为增函数，上斜直线 剪力为减函数，下斜直线
0
上节课主要内容回顾：
2
上节课主要内容回顾：
分布载荷、剪力图和弯矩图之间的规律
1.梁段上无分布载荷：
dFs ( x ) (1) q( x ) 0 dx
剪力图切线斜率为零 Fs为常数，剪力图为平直线
弯矩为一次函数 dM ( x ) (2) Fs ( x ) 常数 弯矩图直线 dx 0 弯矩图为平直线 Fs ( x ) 0 弯矩为增函数，下斜直线
习题6
剪力、弯矩图习题
q A
ql
l
ql RA 6
水平切线
B
ql RB 3
ql
Fs
6
l
M
3
3
3ql 2 27
测验1
q
剪力、弯矩图习题
2qa
A
测验2
F=3KN
a
a
M 0 6KN.m
B
q=2KN/m
C
1m
A
D
4m 1m
B
分布载荷、剪力图和弯矩图之间的规律
2.梁段上的分布载荷为不等于零的常数
dM ( x ) (1) Fs ( x ) 一次函数 dx M ( x ) 为二次函数， 弯矩图为二次曲线
0
q( x )
M ( x ) 应有极小值
弯矩图为上凸曲线
0
M ( x ) 应有极大值
弯矩图为下Байду номын сангаас曲线
例1
q
上节课主要内容回顾：
B
A
RA
ql 2
l
RB
利用剪力、弯矩与分布
Fs
l/2
ql 2
荷载间的积分关系定值
M
ql 2 8
习题1
剪力、弯矩图习题
q
A
Fa
F
a
a
B
解：1）求支座反力
M
B
0 0
RA 2a Fa Fa 0
RA F
M
A
RB 2a Fa Fa 0
RB 0
q
剪力、弯矩图习题 q qa 2 / 2 B A a a
qa
qa RA
2
RB qa
2
Fs
qa / 2 qa / 2
M
qa 2 8
qa 2
2
习题5
A
q
剪力、弯矩图习题 qa
a
RA qa
a
a
B
qa 2
2
RB qa
解：1）求支座反力
MB 0 M
A
5a qa RA 3a qa qa a 0 2 2 RA qa qa a RB 3a qa 2a qa 0 2 2
RA qa
M
A
0 R 2a 2qa2 2qa a 2qa 3a 0 B
RB 5qa
习题3 2qa 2
剪力、弯矩图习题 q 2qa
A
a RA qa
Fs
2a
2qa
B
a RB 5qa
C
qa
3qa
2ql 2
M
2ql 2
习题4
q
剪力、弯矩图习题 q qa 2 / 2 B A a a
RB 2qa
习题2
q
A
剪力、弯矩图习题 q F qa
a
qa
②
a
B
a
RB 2qa
qa
C
RA qa
Fs
① ③ ⑤
⑥
qa M
qa 2 2
④
qa 2 2
习题3 2qa 2
剪力、弯矩图习题 q 2qa
a
RA
A
2a
B
a
C
RB
解：1）求支座反力
2 R 2 a 2 qa 2qa a 2qa a 0 M 0 B A
2
2
0
RB qa
习题5
A
q
剪力、弯矩图习题 qa
a
RA qa
qa
Fs
a
a
B
qa 2
2
RB qa
qa M
qa 2 2
qa 2 2
剪力、弯矩图习题
习题6
q
l
RA ql 6
A
B
ql RB 3
解：1）求支座反力 1 ql RA l l 0 MB 0
3 2
ql RA 6 2 ql RB l l 0 MA 0 3 2 ql RB 3