二三版兼用《运筹学教程》胡运权主编课后习题答案(第八章)

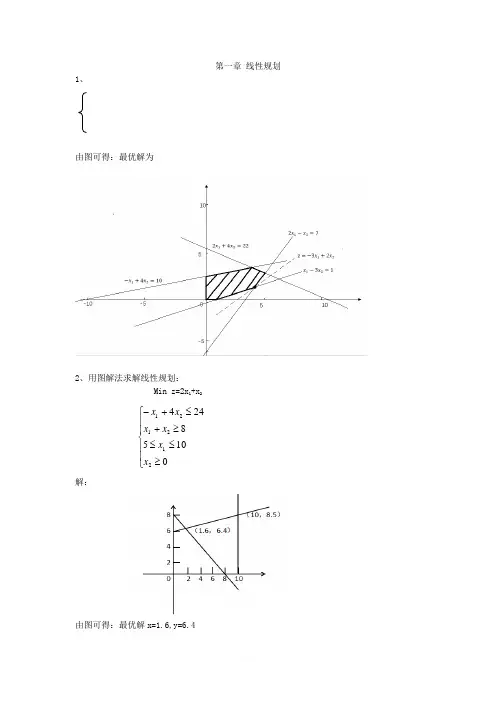
第一章 线性规划1、由图可得：最优解为2、用图解法求解线性规划： Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解：由图可得：最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解：由图可得：最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得：最大值⎪⎩⎪⎨⎧==+35121x x x ， 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示，在（4，2）这一点达到最大值为26将线性规划模型化成标准形式：Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解：令Z ’=-Z,引进松弛变量x 4≥0，引入剩余变量x 5≥0，并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束，321321321321,00632442392-x x x x x x x x x x x x解：令Z ’ = -z ，引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。

运筹学教程（第⼆版）（胡运权）课后答案（清华⼤学出版社）运筹学教程（第⼆版）习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。

并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。

1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解，1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解， x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。

第一章 线性规划1、由图可得：最优解为2、用图解法求解线性规划： Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解：由图可得：最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解：由图可得：最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得：最大值⎪⎩⎪⎨⎧==+35121x x x ， 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示，在（4，2）这一点达到最大值为26将线性规划模型化成标准形式：Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解：令Z ’=-Z,引进松弛变量x 4≥0，引入剩余变量x 5≥0，并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束，321321321321,00632442392-x x x x x x x x x x x x解：令Z ’ = -z ，引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。

《运筹学》第八章图与网络分析习题1.思考题(１)解释下列名词，并说明相互之间的区别与联系：①顶点，相邻，关联边；②环，多重边，简单图；③链，初等链；④圈，初等圈，简单拳；⑤ 回 路，初等路；⑥节点的次，悬挂点，孤立点；⑦）连通图，连同分图， 支 撑子图；⑧有向图，基础图，赋权图。

⑨子图，部分图，真子图．(２)通常用记号Ｇ＝（Ｖ，Ｅ）表示一个图，解释Ｖ及Ｅ的涵义及这个表达式 的涵义．(３)通常用记号Ｄ＝（Ｖ，Ａ）表示一个有向图，解释Ｖ及Ａ的涵义及这个表 达式的涵义．(４) 图论中的图与一般几何图形的主要区别是什么？ (５) 试述树与图的区别与联系．(６) 试述 求最短路问题的Ｄijkstra 算法的基本思想及其计算步骤． (７) 试述寻求最大流的标号法的步骤与方法．(８) 简述最小费用最大流的概念及其求解的基本思想和方法．(９) 通常用记号Ｎ＝（Ｖ，Ａ，Ｃ）表示一个网络，试解释这个表达式的涵义． (10) 在最大流问题中，为什么当存在增广链时，可行流不是最大流？ (11) 试叙述最小支撑树、最大流、最短路等问题能解决那些实际问题。

2.判断下列说法是否正确(1) 图论中的图是为了研究问题中有哪些对象及对象之间的关系，它与图的几何形状无关。

(2) 一个图G 是树的充分必要条件是边数最少的无孤立点的图。

(3) 如果一个图G 从V 1到各点的最短路是唯一的，则连接V 1到各点的最短路，再去掉重复边，得到的图即为最小支撑树。

(4 )图G 的最小支撑树中从V 1到V n 的通路一定是图G 从V 1到V n 的最短路。

(5) {f ij =0}总是最大流问题的一个可行流。

(6 )无孤立点的图一定是连通图。

(7) 图中任意两点之间都有一条简单链，则该图是一棵树。

(8) 求网络最大流的问题总可以归结为求解一个线性规划问题。

(9)在图中求一点Ｖ１到另一点Ｖn 的最短路问题总可以归结为一个整数规划问题 (10) 图G 中的一个点V 1总可以看成是G 的一个子图。