二三版兼用《运筹学教程》胡运权主编课后习题答案(第二章)模板
- 格式:ppt
- 大小:1.75 MB
- 文档页数:47
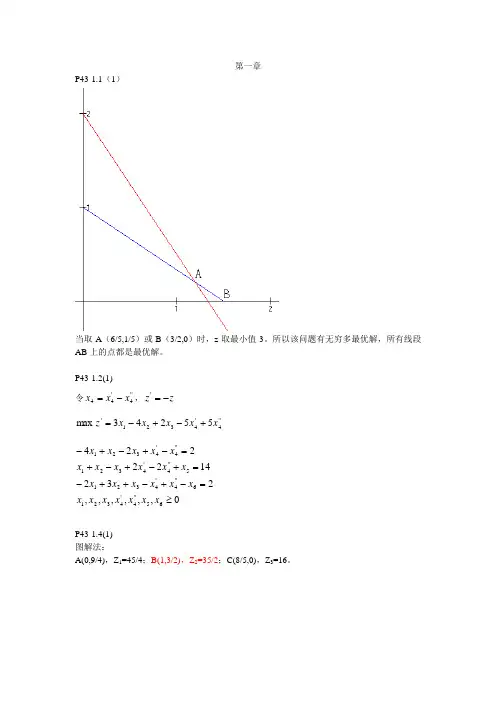
第一章P43-1.1(1)当取A (6/5,1/5)或B (3/2,0)时,z 取最小值3。
所以该问题有无穷多最优解,所有线段AB 上的点都是最优解。
P43-1.2(1)令''4'44x x x -=,z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法:A(0,9/4),Z 1=45/4;B(1,3/2),Z 2=35/2;C(8/5,0),Z 3=16。
单纯形法:10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于:原点;C;B。
P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。
两阶段法:阶段二:P45-1.10证明:CX (0)>=CX*,C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0,即(C*-C)(X*-X (0))>=0。
P45-1.13设饲料i 使用x i (kg ),则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。

运筹学教程(第⼆版)(胡运权)课后答案(清华⼤学出版社)运筹学教程(第⼆版)习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解,1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解, x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。

《运筹学教程》第二章习题答案1、(1)解:引入松弛变量x4≥0,x5≥0,化不等式为等式为:minz=2X1 +3X2+4X3s.t. X1+3X2+2X3+X4=74X1+2X2+X5=9X1,X2,X4,X5≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :minz=2X1 +3X2+4X3′-4X3〞s.t. X1+3X2+2 X3′-2 X3〞+X4=74X1+2X2+X5=9X1,X2, X3′,X3〞,X4,X5 ≥0(2)解:引入松弛变量x5≥0,剩余变量X6≥0,化不等式为等式为:maxz=X1 -5X2+4X3- X4s.t. X1+2X3+X5=7X2-2X4-X6=9X1,X2,X4,X5 ,X6≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :maxz=X1 -5X2+4X3′-4X3〞- X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥0化极大的目标函数为极小的目标函数:minz=-X1+5X2-4X3′+4X3〞+X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥02、(1)是不等式表示下图阴影区域,过阴影部分任意两点的直线仍在该区域内。
(2)不是不等式表示下图阴影区域,过阴影部分且通过曲线上部的直线上的点不完全在该区域内。
(3)不是 不等式表示下图阴影区域,过阴影部分且通过圆内部的直线上的点不完全在该区域内。
3、在以下问题中,指出一组基础变量,求出所有基础可行解以及最优解。
(1)123123123123m ax 2..2644,,0z x x x s t x x x x x x x x x =+-⎫⎪++≤⎪⎬+-≤⎪⎪≥⎭解:将上式化成标准形式,如下:1231234123512345m in 2..2644,,,,0p x x x s t x x x x x x x x x x x x x =--+⎫⎪+++=⎪⎬+-+=⎪⎪≥⎭从上式中可以得出系数矩阵为[]12345112101411A P P P P P ⎡⎤==⎢⎥-⎣⎦, 取基础变量为45,x x ,令非基变量123,,x x x =0,解方程组123412352644x x x x x x x x +++=+-+=得基础可行解(1)(0,0,0,6,4)T x =同理得基础解:(2)(0,6,0,0,20)T x =-,(3)(0,0,3,0,7)T x =,(4)(0,0,4,24,0)T x =-,(5)(0,1,0,5,0)Tx =,(6)1420(0,,,0,0)99Tx =,(7)(6,0,0,0,2)T x =-,(8)(4,0,0,2,0)Tx=,(9)202(,,0,0,0)33Tx =-,(10)142(,0,,0,0)33Tx =。

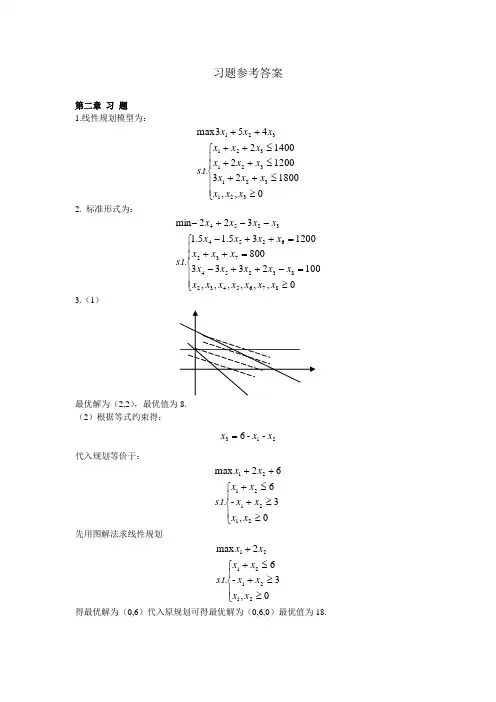
习题参考答案第二章 习 题1.线性规划模型为:⎪⎪⎩⎪⎪⎨⎧≥≤++≤++≤++++0,,1800231200214002..453max 321321321321321x x x x x x x x x x x x t s x x x 2. 标准形式为:⎪⎪⎩⎪⎪⎨⎧≥=-++-=++=++---+-0,,,,,,1002333800120035.15.1..322min 87654328325473262543254x x x x x x x x x x x x x x x x x x x t s x x x x 3.(1)最优解为(2,2),最优值为8.(2)根据等式约束得:213--6x x x =代入规划等价于:⎪⎩⎪⎨⎧≥≥+≤+++0,3-6..62max 21212121x x x x x x t s x x 先用图解法求线性规划⎪⎩⎪⎨⎧≥≥+≤++0,3-6..2max 21212121x x x x x x t s x x 得最优解为(0,6)代入原规划可得最优解为(0,6,0)最优值为18.4.(1)以21,x x 为基变量可得基可行解(3,1,0),对应的基阵为:⎪⎪⎭⎫⎝⎛1101 以31,x x 为基变量可得基可行解(2,0,1),对应的基阵为:⎪⎪⎭⎫ ⎝⎛2111 (2)规划转化为标准形式:⎪⎩⎪⎨⎧≥=++=++--0,,,55623..34min 432142132121x x x x x x x x x x t s x x 以32,x x 为基变量可得基可行解(0,1,4,0),对应的基阵为:⎪⎪⎭⎫⎝⎛0512 5. 以432,,x x x 为基变量可得基可行解(0,2,3,9),对应的典式为:32192231412=+=+=x x x x x 非基变量1x 的检验数为21-。
6. (1) a=0,b=3,c=1,d=0;(2) 基可行解为(0,0,1,6,2) (3)最优值为3.7.(1)最优解为(1.6,0,1.2),最优值为-4.4;(2)令11-=x y ,则0≥y ,11+=y x ,在规划中用1+y 替代1x ,并化标准形式。

运筹学教程(第二版)习题解答8.1 证明在9座工厂之间,不可能每座工厂只与其他3座工厂有业务联系,也不可能只有4座工厂与偶数个工厂有业务联系。
解:将有联系的工厂做一条连线。
如果仅有9座工厂只与其他3座工厂有业务联系,说明顶点次数之和为27,矛盾如果只有4座工厂与偶数个工厂有业务联系,其他5个工厂一定与奇数个工厂有业务联系,说明顶点次数之和还是奇数,矛盾。
8.2 有八种化学药品A、B、C、D、E、F、G、H 要放进贮藏室。
从安全角度考虑,下列各组药品不能贮存在同一室内:A—C,A—F,A—H,B—D,B—F,B—H,C—D,C—G,D—E,D—G,E—G,E—F,F—G,G—H,问至少需要几间贮藏室存放这些药品。
解:能贮存在同一室内的两种药品之间作一条连线。
贮存在同一室内的药品应该构成一个完全图。
ABG,CFH ,DE构成完全图。
故,存放这些药品最少需要 3 间储藏室。
8.36个人围成圆圈就座,每个人恰好只与相邻者不相识,是否可以重新就座,使每个人都与邻座认识?解:两个人认识作一条连线。
8.4判定图8-50中的两个图能否一笔画出,若能,则用图形表示其画法。
解:(a)图都是偶点,可以一笔画出。
(b)图只有两个奇点,一个奇点为起点,另一个奇点为终点。
8.5求解如图8-51所示的中国邮路问题,A点是邮局8.6分别用深探法、广探法、破圈法找出图8-52所示图的一个生成树。
8.7设计如图5-53所示的锅炉房到各座楼铺设暖气管道的路线,使管道总长度最(单位:m)。
8.8分别用避圈法和破圈法求图8-54所示各图的最小树8.9 给定权数1,4,9,16,25,36,49,64,81,构造—棵霍夫曼树。
8.10 如图8-55,v0是一仓库,v9是商店,求一条从v0到v9的最短路。
8.11 求图8-56中v1到各点的最短路8.12 求图8-57网络中各顶点间的最短路8.13 某设备今后五年的价格预测分别是(5,5,6,7,8),若该设备连续使用,其第j 年的维修费分别为(1,2,3,5,6),某单位今年购进一台,问如何确定更新方案可使5年里总支出最小(不管设备使用了多少年,其残值为0)解:最优解为:先使用两年,更新后再使用三年。