平行四边形全章复习知识讲解
- 格式:ppt
- 大小:459.50 KB
- 文档页数:15

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
以下是平行四边形的基本知识点总结:
定义
平行四边形是指具有两组对边分别平行的四边形。
性质
1. 对边平行性质:平行四边形的两组对边分别平行。
2. 对角线性质:平行四边形的对角线互相平分,并且长度相等。
3. 内角和性质:平行四边形的内角的和为180度。
4. 外角性质:平行四边形的外角的和为360度。
5. 对边长度性质:平行四边形的对边长度相等。
6. 同底角性质:与平行四边形的一条边相邻,另一条边平行的两个内角相等。
7. 同旁内角性质:与平行四边形的两条边相邻,另一条边平行的两个内角互补。
判定方法
1. 对边平行判定:如果一个四边形中有两组对边分别平行,则它是一个平行四边形。
2. 对角线平分判定:如果一个四边形的对角线互相平分,并且长度相等,则它是一个平行四边形。
特殊类型
1. 矩形:具有四个内角都为90度的平行四边形。
2. 正方形:具有四个内角都为90度,且四条边长度相等的平
行四边形。
相关公式
1. 平行四边形的面积公式:面积 = 底边长度 ×高度。
2. 平行四边形的周长公式:周长= 2 ×(底边长度+ 侧边长度)。
以上是关于平行四边形的基本知识点总结。
通过了解这些性质
和定理,可以更好地理解和解决相关的数学问题。




平行四边形知识点总结平行四边形是几何中的一种特殊的四边形,具有许多独特的性质和特点。
在学习几何学的过程中,了解平行四边形的各种知识点是非常重要的。
本文将对平行四边形的定义、性质、判定条件、相关定理等知识点进行总结,希望对读者们有所帮助。
一、定义平行四边形是指具有两对对边分别平行的四边形。
换句话说,如果一个四边形的两对对边分别平行,则这个四边形就是平行四边形。
在平行四边形中,相邻的两条边互相平行,而对角线长相等。
此外,平行四边形是菱形和矩形的特殊情况。
二、性质1. 对边平行性:平行四边形的两对对边分别平行。
2. 对角相等性:平行四边形的对角相等,即相对的两个角相等。
3. 交叉角相等性:平行四边形的交叉角相等,即相对的两个对边之间的角相等。
4. 相邻角补角性:平行四边形的相邻角互为补角。
5. 对角和:平行四边形的对角之和为180度。
6. 对角线长相等:平行四边形的对角线长相等。
7. 重心:平行四边形的对角线交点是平行四边形的重心。
8. 对角线相交:平行四边形的对角线彼此相交于中点。
以上是平行四边形的一些基本性质,在解题过程中,可以根据这些性质来判断和推理。
三、平行四边形的判定条件1. 两对对边分别平行根据平行四边形定义可知,平行四边形的判定条件就是具有两对对边分别平行。
2. 对角线长相等对于一个四边形,如果其对角线长相等,则可以判定为平行四边形。
3. 对角相等如果一个四边形的对角相等,则可以判定为平行四边形。
以上是平行四边形的判定条件,可以根据这些条件来判断一个四边形是否为平行四边形。
四、相关定理在学习平行四边形的过程中,还有一些相关定理也是非常重要的。
以下是一些常见的相关定理:1. 单位法则:平行四边形的对边平行,可以利用单位法则进行求解。
2. 等边平行四边形:如果一个四边形的四条边长度相等,则这个四边形是等边平行四边形。
3. 等腰平行四边形:如果一个四边形的两对对边分别平行且具有相等的对边,则这个四边形是等腰平行四边形。
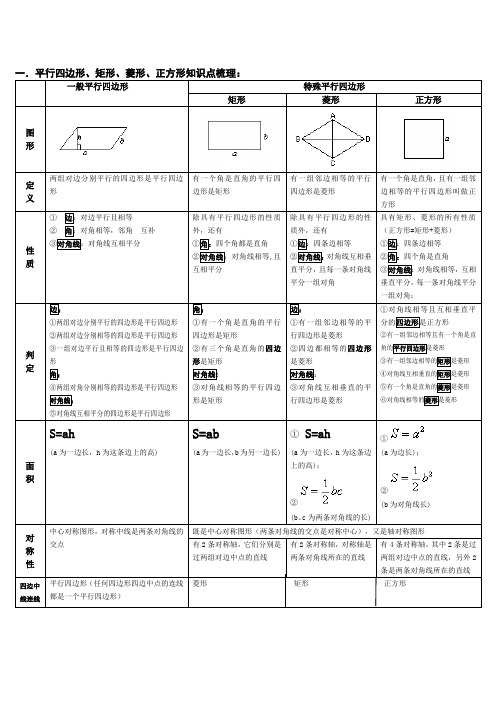
三角形的中位线中位线平行于第三边并且等于第三边的一半一.温故知新平行四边形的面积1)平行四边形ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE=2cm,AF=3cm,求ABCD的面积.2)如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.(1)求证:PA=PC.(2)若BD=12,AB=15,∠DBA=45°,求四边形ABCD的面积.平行四边形与角度如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B′,C′在同一直线上,则∠AEF=度.平行四边形与线段1)如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE 于E点.(1)求证:EF=DF;(2)若AC=2CF,∠ADC=60°,AC⊥DC,求DE的长.2)已知:如图,在▱ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G.(1)求证:AE⊥DF;(2)若AD=10,AB=6,AE=4,求DF的长.平行四边形综合探究:如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F 为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结二.知识讲解1.如图,已知M、N、P、Q分别为AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.2.已知:如图,四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA、EF的延长线交于点M ,CD 、EF 的延长线交于点N.求证:∠AME=∠DNE.3.如图,在△ABC 中,P 是中线AD 的中点,连接BP 并延长交AC 于E ,F 为BE 的中点,求证:AF ∥DE.4.如图,在□ABCD 中,M 是OB 的中点,连接AM 并延长至P.使MP=AM ,连接DP 交AC 于N.求证:(1)MN ∥AD ; (2)S 四边形MPNQ =S △OBC5.如图,AD 是△ABC 的外角平分线,CD ⊥AD 于D ,E 是BC 的中点. 求证:(1)DE ∥AB ; (2)DE=21(AB+AC )6.如图,在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC.对角线相交于点O,∠AOB=60°,且E、 F、M分别是OD、OA、BC的中点.求证:△EFM是等边三角形.。
专题二平面图形类型三平行四边形【知识讲解】1.定义两组对边分别平行且相等,两组对角分别相等,用端点大写字母按顺或逆时针顺序表示,如:平行四边形ABCD(如图1)2.基本公式:平行四边形的周长=2X(长+宽)平行四边形的面积=底乂高3.底和高注意:诈言时委帛三角除上的直角.底土的小方桓表示宜肓.戏;门遷常九它小股凳.只要是宜角既一走要录小枣巽=C2)底利言是一一就应於!艺帚的小視巽畝在邱条边上,它裁是这条边为底时的对应盒;〔幻国d丰.医是DC边的藝应壽,宪对不能说挂是担过並意)【典例精讲】(如图)请回忆老师引导你推导平行四边形面积公式的情境,给(1)、(2)填空;(3)计算。
1A(1)以将平行四边形转化为长方形来推导平行四边形的面积公式,把平行四边形转化成长方形采用的方法是:(2)观察转化前的平行四边形与转化后的长方形,你发现了什么?(请写在下面的横线上,至少写三条)(3)计算上面平行四边形的面积。
(先动手在图中量出计算时需要的数据,再算出它的面积)【答案】(1)剪拼法;(2)长方形的长就是平行四边形的底、长方形的高就是平行四边形的高、长方形的面积等于平行四边形的面积.(3)平行四边形的底是2厘米,高是1厘米,平行四边形的面积=2x1=2(平方厘米)。
答:平行四边形的面积是2平方厘米。
【解析】(1)从左边沿平行四边形的高剪下一个直角三角形,拼到平行四边形的右侧,就形成了一个长方形,从而利用剪拼法就可以推导出平行四边形的面积计算公式。
(2)观察转化前的平行四边形与转化后的长方形,发现:长方形的长等于平行四边形的底、长方形的高等于平行四边形的高、长方形的面积等于平行四边形的面积;(3)分别量出平行四边形的底和高,就可以计算其面积。
【巩固练习】一、选择题。
1.在一个平行四边形里,其中两条边的长度分别是8厘米和5厘米.这个平行四边形的周长是()。
2.—个平行四边形的一组邻边分别长8厘米和12厘米,平行四边形的一条高A.13厘米B.40厘米C.26厘米是10厘米,这个平行四边形的面积是()。
教师:学生:时间:_ 2016 _年_ _月日段第__ 次课
ABCD中,延长
随堂练习三:
.若平行四边形的两邻边的长分别为
17在ABCD中,AB比AD大2,∠DAB的角平分线AE交CD于E,∠ABC的角平分线BF交CD于F,若平行四边形ABCD的周长为24,求CE、FD、EF的长
19已知:如图,ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF 是平行四边形.
20、如图,□ABCD的对角线AC、BD交于O,EF过点O交AD于E,交BC于F,G是OA的中点,H是OC的中点,四边形EGFH是平行四边形吗?说明理由.
21.如图,平行四边形ABCD中,M、N分别为AD、BC的中点,连结AN、DN、BM、CM,且AN、BM交于点P,CM、DN交于点Q.四边形MGNP是平行四边形吗?为什么?
22.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD•为边作等边△ADE.(1)求证:△ACD≌△CBF;
(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°?•证明你的结论.
23已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.。
北师大版八年级数学(下)第六章平行四边形6.2平行四边形的判定(1)学校:xxxxxxxxx中学授课人:xxx学习目标1.会证明平行四边形的两种判定定理2.理解平行四边形的两种判定定理3.能够熟练运用平行四边形的两种判定定理复习导入复习:1.什么是平行四边形?两组对边分别平行的四边形是平行四边形2.平行四边形的性质有那些?边:对边平行且相等角:对角相等,邻角互补对角线:互相平分对称性:是中心对称图形,对角线的交点是对称中心问题思考:取四个纸条,其中两根长度相等,另外两根长度也相等,能否在平面内将四个纸条首尾相连组成一个平行四边形?结论:两组对边分别相等的四边形是平行四边形定理: 两组对边分别相等的四边形是平行四边形已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.A DC B ∵AB=CD,AD=BC,BD=DB,在△ABD和△CDB中,证明:如图,连接BD.∴ △ABD≌ △CDB.∴∠ABD=∠CDB,∠ADB=∠CB∴AB∥CD,AD ∥CB∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)定理:两组对边分别相等的四边形是平行四边形几何语言:在四边形ABCD中,∵AB=CD,AD=BC∴四边形ABCD是平行四边形新授课议一议:(1)取两个长度相等的细纸条,你能将它们摆放在一个平面上,使得这两个细木条的四个端点恰好是一个平行四边形的四个顶点吗?能,只要将两根长度相等的细纸条平行摆放就可以使这两根细纸条的四个端点恰好是一个平四边形的四个顶点.(2)如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?与同伴交流另一组对边相等或者该组对边平行.定理: 一组对边平行且相等的四边形是平行四边形已知:如图,在四边形ABCD中,AB∥CD.求证:四边形ABCD是平行四边形.A DC B ∴∠BAC=∠DCA,∵AB∥CD 证明:如图,连接AC.又∵AB=CD,AC=CA∴△ABC=△CDA∴BC=DA∴四边形ABCD是平行四边形.(两组对边分别相等的四边形是平行四边形)已知:如图,在四边形ABCD中,AB∥CD.求证:四边形ABCD是平行四边形.A DC B ∴∠BAC=∠DCA,∵AB∥CD证明:如图,连接AC.又∵AB=CD,AC=CA∴△ABC=△CDA ∴∠DAC=∠BCA∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)∴AD∥BC定理:一组对边平行且相等的四边形是平行四边形几何语言:在四边形ABCD中,∵AB∥CD∴四边形ABCD是平行四边形1.如图,AB=CD (1)当AB CD时,可以说明四边形ABCD是平行四边形 (2)当AD BC时,可以说明四边形ABCD是平行四边形随堂检测A B C D F E D C A B 证明: ∵ 四边形ABCD是平行四边形∵E,F分别为AD和CB的中点∴AD=CB(平行四边形的对边相等)AD∥CB(平行四边形的定义)∥=2.已知,如图,在平行四边形ABCD中,E,F分别为AD和CB的中点.求证:四边形BFDE是平行四边形∴DE=BF∴四边形BFDE是平行四边形3.判断:一组对边相等,另一组对边平行的四边形是平行四边形。