九年级数学特殊三角形复习(201911)
- 格式:ppt
- 大小:141.00 KB
- 文档页数:13


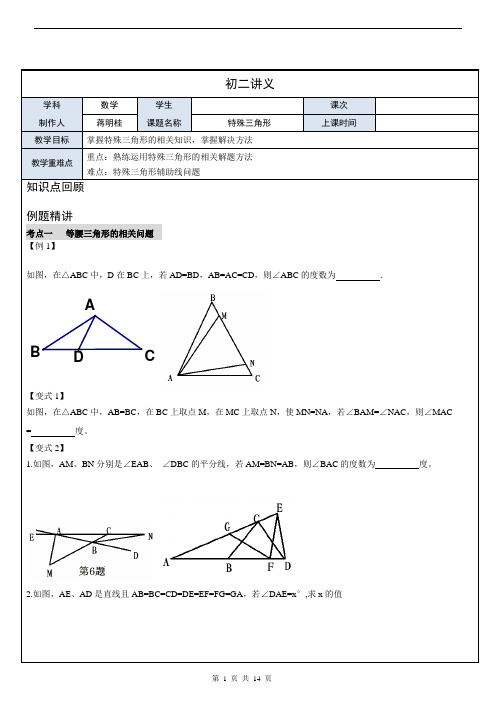
初二讲义学科 数学 学生 课次制作人 蒋明桂课题名称特殊三角形上课时间教学目标 掌握特殊三角形的相关知识,掌握解决方法 教学重难点重点:熟练运用特殊三角形的相关解题方法 难点:特殊三角形辅助线问题知识点回顾例题精讲考点一 等腰三角形的相关问题 【例1】如图,在△ABC 中,D 在BC 上,若AD=BD ,AB=AC=CD ,则∠ABC 的度数为 .【变式1】如图,在△ABC 中,AB=BC ,在BC 上取点M ,在MC 上取点N ,使MN=NA ,若∠BAM=∠NAC ,则∠MAC = 度。
【变式2】1.如图,AM 、BN 分别是∠EAB 、 ∠DBC 的平分线,若AM=BN=AB ,则∠BAC 的度数为 度。
2.如图,AE 、AD 是直线且AB=BC=CD=DE=EF=FG=GA ,若∠DAE=x °,求x 的值BCAD【例2】等腰三角形的一个外角等于,则这个三角形的三个内角分别为 。
【变式1】在等腰三角形中,如果顶角是一个底角的2倍,那么顶角等于_____度;如果一个底角是顶角的2倍,那么顶角等于_______度;如果一个角是另一个角的2倍,那么顶角等于_____度.【例3】等腰三角形一腰上的高等于该三角形某一条边的长度的一半,则其顶角等于( ) A .30° B .30°或150°C . 120°或150° D .30°或120°或150°【变式1】1.有一顶角为36°的等腰△ABC ,AB=AC ,周长为28,一边长为10,一底角平分线与腰交与D 点,BD 的长度为___________。
2.若等腰三角形一腰上的高与另一腰的夹角为300,腰长为a ,则其底边上的高是 。
【变式2】如图,△ABC 中,AB=AC ,∠ABC=36°,边AC 绕点A 逆时针旋转60°,至AD 的位置,作∠ACE=12°,交BD 于点E ,连结AE .试判定△AEC 是什么三角形?请说明理由.CDEBA【例4】如图,△ABC 中,AD 平分∠BAC ,BP ⊥AD 于P ,AB=5,BP=2,AC=9。

中考复习特殊三角形中考对于每一位初中生来说都是一次重要的挑战,而数学中的特殊三角形更是考点中的重点。
特殊三角形包括等腰三角形、等边三角形和直角三角形,它们各自具有独特的性质和判定方法。
接下来,让我们一起深入复习这些特殊三角形的知识。
一、等腰三角形等腰三角形是指至少有两边相等的三角形。
相等的两条边称为这个三角形的腰,另一边称为底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
1、性质(1)等腰三角形的两腰相等。
(2)等腰三角形的两底角相等(简写成“等边对等角”)。
(3)等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)。
2、判定(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
(2)有两条边相等的三角形是等腰三角形。
在解题中,我们常常利用等腰三角形的性质和判定来求解角度、边长等问题。
例如,已知一个等腰三角形的顶角为 80°,那么底角的度数就可以通过“(180°顶角)÷ 2”来计算,即(180° 80°)÷ 2 = 50°。
二、等边三角形等边三角形又称正三角形,为三边相等的三角形,其三个内角相等,均为 60°。
1、性质(1)等边三角形的三条边都相等。
(2)等边三角形的三个内角都相等,且均为 60°。
(3)等边三角形是轴对称图形,有三条对称轴。
2、判定(1)三边相等的三角形是等边三角形。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是 60°的等腰三角形是等边三角形。
等边三角形在实际问题中也有广泛的应用。
比如在建筑设计中,利用等边三角形的稳定性可以增强结构的牢固性。
三、直角三角形直角三角形是一个角为直角的三角形。
直角所对的边称为斜边,其余两边称为直角边。
1、性质(1)直角三角形两直角边的平方和等于斜边的平方(勾股定理)。
(2)在直角三角形中,两个锐角互余。

中考内容中考要求ABC等腰三角形与直角三角形了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形;理解等腰三角形、等边三角形、直角三角形的性质和判定能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题 会运用等腰三角形、等边三角形、直角三角形的知识解决有关问题⎧⎧⎧⎪⎪⎪⎧⎪⎪⎪⎨⎨⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎩⎪⎪⎪⎧⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎪⎪⎨⎪⎪⎩⎩定义等边对等角等腰三角形性质三线合一等腰三角形判定定义特殊三角形等边三角形性质判定定义直角三角形性质判定一、 等腰三角形1、定义:有两边相等的三角形是等腰三角形.相等的两边叫做腰,第三边为底.2、性质:(1)轴对称性:等腰三角形是轴对称图形,有1条对称轴. (2)定理1:等腰三角形的两个底角相等,简称“等边对等角”.(3)定理2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”. 3、判定:如果一个三角形有两角相等,那么这两个角所对的边也相等,简称“等角对等边”.知识精讲中考大纲 特殊三角形知识网络图【补充】1、等腰三角形两腰上的高相等;2、等腰三角形两腰上的中线相等;3、等腰三角形两底角的平分线相等;二、等边三角形1、定义:三边相等的三角形是等边三角形.2、性质:(1)轴对称性:等边三角形是轴对称图形,有3条对称轴.(2)等边三角形的各角都相等,并且每一个角都等于60°.3、判定:(1)判定1:三个角都相等的三角形是等边三角形.(2)判定2:有一个角等于60°的等腰三角形是等边三角形.三、线段的垂直平分线1、定义:经过线段中点并且垂直于这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2、性质:线段垂直平分线上的点与这条线段两个端点的距离相等.3、判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.4、实质构成:线段的垂直平分线可以看作到线段两个端点距离相等的所有点的集合.四、直角三角形1、直角三角形30°角所对的边等于斜边的一半.2、直角三角形斜边的中线等于斜边的一半.解题方法技巧1、等腰三角形一腰上的高与底边的夹角等于顶角的一半.AC 2、等腰三角形顶角的外角平分线与底边平行3、等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.如图,即DE DF BG +=.本结论可以用面积列等式推得.ABCABCDE F G4、等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高.5、要证明一个三角形是等腰三角形,必须得到两边相等,得到两边相等的方法主要有:(1)通过等角对等边;(2)通过三角形全等得两边相等;(3)利用垂直平分线的性质得到两边相等.1、遇到等腰三角形的问题时,注意边有腰与底之分,角有底角和顶角之分.2、遇到高线的问题要考虑高在形内和形外两种情况.3、等腰三角形三线合一定理没有逆定理,定理的逆推论需要用全等去证明.易错点辨析题型一:等腰三角形的性质与判定【例1】 已知ABC △中,AB AC =.36A ∠=︒,则C ∠______. 【例2】 等腰三角形一个底角为75°,它的另外两个角为_______. 【例3】 等腰三角形一个角为70°,它的另外两个角为__________. 【例4】 已知等腰三角形的周长为24cm ,一腰长是底边长的2倍,则腰长是( ) A .4.8cm B .9.6cm C .2.4cm D .1.2cm【例5】 在等腰ABC △中,AB AC =,其周长为20cm ,则AB 边的取值范围是__________.(2014年玉林中考)【例6】 如图,在ABC △中,AB AC =,且D 为BC 上一点,CD AD =,AB BD =,则B ∠的度数为__________.(2014年南充中考)DCBA【例7】 如图,在Rt ABC △中,D E ,为斜边AB 上的两个点,且BD BC AE AC ==,,则DCE ∠的大小为__________.(2014年天津)EDCBA【例8】 如图,ABC ∆中,30A ∠=︒,CD 是BCA ∠的平分线,ED 是CDA ∠的平分线,EF 是DEA ∠的平分线,DF FE =,求B ∠.ABCDEF特殊三角形习题集课堂练习【例9】 如图,P 为等腰三角形ABC 的底边AB 上的任意一点,PE AC ⊥于点E ,PF ⊥BC 于点F ,AD BC ⊥点D ,求证:PE PF AD +=.ABCE D PF【例10】 如图,点P 为等腰三角形ABC 的底边BA 的延长线上的一点,PE CA ⊥的延长线于点E ,PF BC⊥于点F ,AD BC ⊥于点D .PE 、PF 、AD 之间存在着怎样的数量关系?ABCEDP F【例11】 如图所示,已知ABC △中,D 、E 为BC 边上的点,且AD AE =,BD EC =,求证:AB AC =.AB CD E【例12】 如图,请在下列四个等式中,选出两个作为条件,推出AED △是等腰三角形,并予以证明.(写出一种即可)等式:①AB DC =,②BE CE =,③B C ∠=∠,④BAE CDE ∠=∠. 已知:____________________ 求证:AED △是等腰三角形. 证明:【例13】 如图1,已知矩形ABED ,点C 是边DE 的中点,且2AB AD =.(1)判断ABC △的形状,并说明理由;(2)保持图1中ABC △固定不变,绕点C 旋转DE 所在的直线MN 到图2中(当垂线段AD 、BE 在直线MN 的同侧),试探究线段AD 、BE 、DE 长度之间有什么关系?并给予证明; (3)保持图2中ABC △固定不变,继续绕点C 旋转DE 所在的直线MN 到图3中的位置(当垂线段AD 、BE 在直线MN 的异侧).试探究线段AD 、BE 、DE 长度之间有什么关系?并给予证明.(2010年临沂)题型二:等腰三角形的作图题【例14】 已知ABC ∆中,90A ∠=︒,67.5B ∠=︒.请画一条直线,把这个三角形分割成两个等腰三角形.(请你利用下面给出的备用图,画出两种不同的分割方法.只需画图,不必说明理由,但要在图中标出相等两角的度数).CB ACB A【例15】 已知菱形ABCD 中,72A ∠=︒,请设计两种不同的分法,将菱形ABCD 分割成四个三角形,使得分割成的每个三角形都是等腰三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,例如第20题图,不要求写出画法,不要求证明.)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.36︒36︒36︒18︒18︒54︒72︒72︒72︒54︒DCBAA分A BC D分法2A BC D分法1题型三:等边三角形的性质【例16】 如图,DAC △和EBC △均是等边三角形,AE 、BD 分别与CD 、CE 交于点M 、N ,有如下结论:① ACE DCB △≌△;②CM CN =;③AC DN =.其中正确结论的个数是_____ A . 3个 B .2个 C .1个 D .0个NM ED BA【例17】 如图,在等边ABC △中,点D E ,分别在边BC AB ,上,BD AE =,AD 与CE 交于点F .(1)求证:AD CE =; (2)求DFC ∠的度数.FE DCBA【例18】 如图,已知ABC △为等边三角形,D 、E 、F 分别在边BC 、CA 、AB 上,且DEF ∆也是等边三角形.除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.F EDCBA【例19】 已知,如图,延长ABC △的各边,使得BF AC =, AE CD AB ==,顺次连接D ,E ,F ,得到DEF △为等边三角形.求证:(1)AEF △≌CDE △; (2)ABC △为等边三角形.F DECB A【例20】 如下图,ABC ∆是等边三角形,122CBF ACD BAE ∠∠∠=∶∶∶∶,38DEF DFE ∠-∠=︒.求出DEF∆的每个内角度数.FEDCBA【例21】 如图,三角形ABC 中,AB BC CA ==,AE CD =,AD ,BE 相交于P ,BQ 垂直AD 于Q ,求证:2BP PQ =.P QA BC DE【例22】 如图,在等边ABC △中,点D E ,分别在边BC AB ,上,BD AE =,AD 与CE 交于点F .(1)求证:AD CE =;(2)求DFC ∠的度数.FE DCBA题型四:直角三角形的性质与判定【例23】 在Rt ABC ∆中,90C ∠=︒,30A ∠=︒,6cm BC AB +=,则AB =_______cm .【例24】 如图,在Rt ABC ∆中,9060B ACB D ∠=︒∠=︒,,是BC 延长线上一点,且AC CD =,则:BC CD =_________.DCBA【例25】 若AD 为ABC ∆的高,且1AD =,1BD =,DC BAC ∠=____________.【例26】 已知:如图,在ABC △中,AB BC =,90ABC ∠=︒.F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接AE 、EF 和CF . (1)求证:AE CF =;(2)若30CAE ∠=︒,求EFC ∠的度数.FECBA【例27】 如图,在ABC ∆中,BF AC ⊥于F ,CG AB ⊥于G D E ,,分别是BC FG ,的中点.求证:DE GF ⊥.GFE D CB A【练1】 等腰三角形的一边长为3cm ,另一边长为4cm ,则它的周长是 ___________.【练2】 如图,ABC ∆和BDE ∆都是等边三角形,AB BD <,若ABC ∆不 动,将BDE ∆绕点B 旋转,则在旋转过程中,AE 与CD 的大小关系为( ).A . AE CD =B . AE CD >C . AE CD < D . 无法确定EDCBA【练3】 MON ∠是一个钢架,10MON ∠=︒,在其内部添加一些钢管BC ,CD ,DE ,EF ,FG ,…添加的钢管长度都与OB 相等.(1)当添加到第五根钢管时,求FGM ∠的度数.(2)假设OM 、ON 足够长,能无限地添加下去吗?如果能,请说明理由.如果不能,则最多能添加几根?D NMFEO CBG【练4】 如图,在ABC ∆中,AB AC =,D 是ABC ∆外的一点,且60ABD ∠=,60ACD ∠=.求证:BD DC AB +=.DCBA课后作业【练5】 如图,在Rt ABC ∆中,90BAC ∠=,CA BA =,15DAC DCA ∠=∠=,求证:BA BD =.DACB【练6】 如图ABC △中,AD 平分BAC ∠,DG BC ⊥且平分BC ,DE AB ⊥于E ,DF AC ⊥于F .⑴说明BE CF =的理由;⑵如果AB a =,AC b =,求AE ,BE 的长.GFE DC BA。

三角形九年级总复习知识点三角形是我们数学学科中的一个重要概念,它在几何图形的研究中起着重要的作用。
本文将总结九年级的三角形知识点,帮助同学们进行复习。
1. 三角形的基本定义和分类三角形是由三条线段组成的图形,每条线段称为三角形的边。
根据三条边的长度关系,我们可以将三角形分为等边三角形、等腰三角形和普通三角形。
- 等边三角形的三条边长度相等。
- 等腰三角形的两条边长度相等。
- 普通三角形的三条边长度都不相等。
2. 三角形的角度性质三角形的三个内角之和为180度。
同时,我们还可以根据角的大小将三角形进行分类。
- 锐角三角形:三个内角都小于90度。
- 直角三角形:一个内角为90度。
- 钝角三角形:三个内角中有一个大于90度。
3. 三角形的面积计算计算三角形的面积是我们经常需要处理的问题,其中最常用的方法是使用海伦公式:面积= √[p × (p - a) × (p - b) × (p - c)]其中,p是三角形的半周长,a、b、c分别是三角形的三条边的长度。
4. 相似三角形相似三角形是指具有相同形状但大小不同的三角形。
它们的边与边之比保持一致,角与角之比也相等。
相似三角形的性质在实际问题的解决中具有重要的作用。
5. 三角形的勾股定理勾股定理是三角形中一个重要的定理,它描述了直角三角形中直角边的关系。
勾股定理表达式为:c² = a² + b²其中,a和b是直角三角形的两条直角边的长度,c是斜边的长度。
6. 三角形的角平分线与垂直平分线三角形的角平分线是指将三角形的一个角分成两个相等的角的线段。
垂直平分线则是指将三角形一边的中点与对边的垂直平分线的交点。
这些概念在三角形中有很多应用,例如定位角平分线的交点可以作为三角形内心,垂直平分线的交点可以作为三角形的垂心。
7. 应用题示例在实际问题中,我们常常需要运用三角形的知识进行解决。
下面是一个应用题的示例:甲、乙两位朋友分别站在一座塔的两端,他们之间的距离是200米,塔的高度为150米。