维纳滤波 Wiener Filtering
- 格式:ppt
- 大小:236.00 KB
- 文档页数:20

附录ADAPTIVE WIENER FILTERING APPROACH FOR SPEECHENHANCEMENTM. A. Abd El-Fattah*, M. I. Dessouky , S. M. Diab and F. E. Abd El-samie #Department of Electronics and Electrical communications, Faculty of ElectronicEngineering Menoufia University, Menouf, EgyptE-mails:************************,#*********************ABSTRACTThis paper proposes the application of the Wiener filter in an adaptive manner inspeech enhancement. The proposed adaptive Wiener filter depends on the adaptation of the filter transfer function from sample to sample based on the speech signal statistics(meanand variance). The adaptive Wiener filter is implemented in time domain rather than infrequency domain to accommodate for the varying nature of the speech signal. Theproposed method is compared to the traditional Wiener filter and spectral subtractionmethods and the results reveal its superiority.Keywords: Speech Enhancement, Spectral Subtraction, Adaptive Wiener Filter1 INTRODUCTIONSpeech enhancement is one of the most important topics in speech signal processing.Several techniques have been proposed for this purpose like the spectral subtraction approach, the signal subspace approach, adaptive noise canceling and the iterative Wiener filter[1-5] . The performances of these techniques depend on quality andintelligibility of the processed speech signal. The improvement of the speech signal-tonoise ratio (SNR) is the target of most techniques.Spectral subtraction is the earliest method for enhancing speech degraded by additive noise[1]. This technique estimates the spectrum of the clean(noise-free) signal by the subtraction of the estimated noise magnitude spectrum from the noisy signal magnitude spectrum while keeping the phase spectrum of the noisy signal. The drawback of this technique is the residual noise.Another technique is a signal subspace approach [3]. It is used for enhancing a speech signal degraded by uncorrelated additive noise or colored noise [6,7]. The idea of this algorithm is based on the fact that the vector space of the noisy signal can be decomposed into a signal plus noise subspace and an orthogonal noise subspace.Processing is performed on the vectors in the signal plus noise subspace only, while the noise subspace is removed first. Decomposition of the vector space of the noisy signal is performed by applying an eigenvalue or singular value decomposition or by applying the Karhunen-Loeve transform (KLT)[8]. Mi. et. al. have proposed the signal / noise KLT based approach for colored noise removal[9]. The idea of this approach is that noisy speech frames are classified into speech-dominated frames and noise-dominated frames. In the speech-dominated frames, the signal KLT matrix is used and in the noise-dominated frames, the noise KLT matrix is used.In this paper, we present a new technique to improve the signal-to-noise ratio in the enhanced speech signal by using an adaptive implementation of the Wiener filter. This implementation is performed in time domain to accommodate for the varying nature of the signal.The paper is organized as follows: in section II, a review of the spectral subtraction technique is presented. In section III, the traditional Wiener filter in frequency domain is revisited. Section IV, proposes the adaptive Wiener filtering approach for speech enhancement. In section V, a comparative study between the proposed adaptive Wiener filter, the Wiener filter in frequency domain and the spectral subtraction approach ispresented.2 SPECTRAL SUBTRACTIONSpectral subtraction can be categorized as a non -parametric approach, which simply needs an estimate of the noise spectrum. It is assume that there is an estimate of the noise spectrum that is typically estimated during periods of speaker silence. Let x (n ) be a noisy speech signal :x (n ) = s (n ) + v (n ) (1) where s (n ) is the clean (the noise -free) signal, and v (n ) is the white gaussian noise. Assume that the noise and the clean signals are uncorrelated. By applying the spectral subtraction approach that estimates the short term magnitude spectrum of the noise -freesignal ()ωS by subtraction of the estimated noise magnitude spectrum )(ˆωVfrom the noisy signal magnitude spectrum ()ωX It is sufficient to use the noisy signal phase spectrum as an estimate of the clean speech phase spectrum,[10]:()()()()()()ωωωωX j N X S ∠-=exp ˆˆ (2) The estimated time -domain speech signal is obtained as the inverse Fourier transform of ()ωSˆ. Another way to recover a clean signal s (n ) from the noisy signal x(n ) using the spectral subtraction approach is performed by assuming that there is an the estimate of the power spectrum of the noise Pv ( ω) , that is obtained by averaging over multiple frames of a known noise segment. An estimate of the clean signal short -time squared magnitude spectrum can be obtained as follow [8]:()()()()()⎪⎩⎪⎨⎧≥--=otherwisev P X if v P X S ,00ˆ,ˆˆ222ωωωωω (3) It is possible combine this magnitude spectrum estimate with the measured phase and then get the Short Time Fourier Transform (STFT) estimate as follows:()()()ωωωX j e S S∠=ˆˆ (4) A noise -free signal estimate can then be obtained with the inverse Fourier transform. This noise reduction method is a specific case of the general technique given by Weiss, et al. and extended by Berouti , et al.[2,12].The spectral subtraction approach can be viewed as a filtering operation where high SNR regions of the measured spectrum are attenuated less than low SNR regions. This formulation can be given in terms of the SNR defined as:()()ωωv P X SNR ˆ2= (5) Thus, equation (3) can be rewritten as:()()()()()1222211ˆˆ-⎥⎦⎤⎢⎣⎡+≈-=SNR X X v P X S ωωωωω (6) An important property of noise suppression using spectral subtraction is that the attenuation characteristics change with the length of the analysis window. A common problem for using spectral subtr action is the musicality that results from the rapid coming and going of waves over successive frames [13].3 WIENER FILTER IN FREQUNCY DOMAINThe Wiener filter is a popular technique that has been used in many signal enhancement methods. The basic principle of the Wiener filter is to obtain a clean signal from that corrupted by additive noise. It is required estimate an optimalfilter for the noisy input speech by minimizing the Mean Square Error (MSE) between the desired signal s(n) and the estimated signal s ˆ(n ) . The frequency domain solution to this optimization problem is given by[13]:()()()()ωωωωPv Ps Ps H += (7) where Ps (ω) and Pv (ω) are the power spectral densities of the clean and the noise signals, respectively. This formula can be derived considering the signal s and the noise signal v as uncorrelated and stationary signals. The signal -to -noise ratio is defined by[13]:()()ωωv P Ps SNR ˆ= (8) This definition can be incorporated to the Wiener filter equation as follows:()111-⎥⎦⎤⎢⎣⎡+=SNR H ω (9) The drawback of the Wiener filter is the fixed frequency response at all frequencies and the requirement to estimate the power spectral density of the clean signal and noise prior to filtering.4 THE PROPOSED ADAPTIVE WIENER FILTERThis section presents and adaptive implementation of the Wiener filter which benefits from the varying local statistics of the speech signal. A block diagram of the proposed approach is illustrated in Fig. (1). In this approach, the estimated speech signal mean x mand variance 2x σare exploited.Figure 1: Typical adaptive speech enhancement system for additive noise reductionIt is assumed that the additive noise v(n) is of zero mean and has a white nature withvariance of 2x σ.Thus, the power spectrum Pv (ω) can be approximated by:()2v Pv σω= (10)Consider a small segment of the speech signal in which the signal x(n) is assumed to be stationary, The signal x(n) can be modeled by:()()n m n x x x ωσ+= (11)where x m and x σ are the local mean and standard deviation of x(n). w(n) is a unit variance noise.Within this small segment of speech, the Wiener filter transfer function can be approximated by:()()()()222vs s Pv Ps Ps H σσσωωωω+=+= (12) From Eq.(12), because H(ω) is constant over the small segment of speech, the impulse response of the Wiener filter can be obtained by:()()n n h vs s δσσσ222+= (13) From Eq.(13), the enhanced speech ()n Sˆ within this local segment can be expressed as:()()()()()()x v s s x v s s x x m n x m n m n x m n S -++=+*-+=222222ˆσσσδσσσ (14)If it is assumed that mx and σ s are updated at each sample, we can say:()()()()()()()n m n x n n n m n S x v s s x -++=222ˆσσσ (15) In Eq.(15), the local mean mx (n ) and (x (n ) − mx (n )) are modified separately fromsegment to segment and then the results are combined. If 2v σ is much larger than 2v σ theoutput signal s ˆ(n ) is assumed to be primarily due to x(n) and the input signal x (n) is not attenuated. If 2s σ is smaller than 2v σ , the filtering effect is performe.Notice that mx is identical to ms when mv is zero. So, we can estimate mx (n) in Eq.(15) from x (n) by:()()()()∑+-=+==M n Mn k x s k x M n m n m 121ˆˆ (16) where (2M +1) is the number of samples in the short segment used in the estimation.To measure the local signal statistics in the system of Figure 1, the algorithm developed uses the signal variance 2s σ. The specific method used to designing thespace -variant h(n) is given by(17.b).Since 222v s x σσσ+= may be estimated from x (n) by:()()()⎩⎨⎧>-=otherwise n if n n v v v x s,0ˆˆ,ˆˆˆ22222σσσσσ (17.a)Where()()()()()∑+-=-+=M n M n k x xn m k x M n 22ˆ121ˆσ (17.b) By this proposed method, we guarantee that the filter transfer function is adapted from sample to sample based on the speech signal statistics.5 EXPERIMENTAL RESULTSFor evaluation purposes, we use different speech signals like the handel, laughter and gong signals. White Gaussian noise is added to each speech signal with different SNRs. The different speech enhancement algorithms such as the spectral subtraction method, the Weiner filter in frequency domain and the proposed adaptive Wiener filter are carried out on the noisy speech signals. The peak signal to noise ratio (PSNR)results for each enhancement algorithm are compared.In the first experiment , all the above-mentioned algorithms are carried out on the Handle signal with different SNRs and the output PSNR results are shown in Fig. (2). The same experiment is repeated for the Laughter and Gong signals and the results are shown in Figs.(3) and (4), respectively.From these figures, it is clear that the proposed adaptive Wiener filter approach has the best performance for different SNRs. The adaptive Wiener filter approach gives about 3-5 dB improvement at different values of SNR. The nonlinearity between input SNR and output PSNR is due to the adaptive nature of the filter.Figure 2:PSNR results for white noise case at-10 dB to +35 dB SNR levels for Handle signalFigure 3: PSNR results for white noise case at -10 dB to +35 dB SNR levels for Laughter signalFigure 4:PSNR results for white noise case at -10 dB to +35 dB SNR levels for Gong signalThe results of the different enhancement algorithms for the handle signal with SNRs of 5,10,15 and 20 dB in the both time and frequency domain are given in Figs. (5) to (12). These results reveal that the best performance is that of the proposed adaptive Wiener filter.Figure 5: Time domain results of the Handel sig. At SNR = +5dB (a) original sig. (b) noisy sig. (c) spectral subtraction. (d) Wiener filtering. (e) adaptive WienerFiltering.Figure 6:The spectrum of the Handel sig. in Fig.(5) (a) original sig. (b) noisy sig. (c) spectral subtraction. (d) Wiener filtering. (e) adaptive Wiener filtering.Figure 7: Time domain results of the Handel sig. At SNR = 10 dB (a) original sig. (b) noisy sig. (c) spectral subtraction. (d) Wiener filtering. (e) adaptive Wiener filtering.Figure 8: The spectrum of the Handel sig. in Fig.(7)(a) original sig. (b) noisy sig. (c) spectral subtraction. (d)Wiener filtering. (e) adaptive Wiener filtering.Figure 9: Time domain results of the Handel sig. At SNR = 15 dB (a) original sig. (b) noisy sig. (c) spectral subtraction. (d) Wiener filtering. (e) adaptive Wiener filtering.Figure 10: The spectrum of the Handel sig. in Fig.(9)(a) original sig. (b) noisy sig. (c) spectral subtraction. (d)Wiener filtering. (e) adaptive Wiener filtering.Figure 11: Time domain results of the Handel sig. At SNR = 20 dB (a) original sig. (b) noisy sig. (c) spectral subtraction. (d) Wiener filtering. (e) adaptive WienerFiltering.Figure 12:The spectrum of the Handel sig. in Fig.(11)(a) original sig. (b) noisy sig. (c) spectral subtraction. (d)Wiener filtering. (e) adaptive Wiener filtering.6 CONCLUSIONAn adaptive Wiener filter approach for speech enhancement is proposed in this papaper. This approach depends on the adaptation of the filter transfer function from sample to sample based on the speech signal statistics(mean and variance). This results indicates that the proposed approach provides the best SNR improvementamong the spectral subtraction approach and the traditional Wiener filter approach in frequency domain. The results also indicate that the proposed approach can treat musical noise better than the spectral subtraction approach and it can avoid the drawbacks of Wiener filter in frequency domain .自适应维纳滤波方法的语音增强摘要本文提出了维纳滤波器的方式应用在自适应语音增强。

维纳滤波原理维纳滤波是一种信号处理中常用的滤波方法,它的原理是基于最小均方误差准则,通过对信号和噪声的统计特性进行分析,设计一种能够最小化系统输出与期望输出之间均方误差的滤波器。
维纳滤波在图像处理、语音处理、雷达信号处理等领域都有广泛的应用,下面我们来详细了解一下维纳滤波的原理和应用。
首先,我们需要了解维纳滤波的基本模型。
维纳滤波的输入信号可以表示为s(n),噪声信号表示为v(n),系统输出信号表示为x(n),那么维纳滤波器的输出可以表示为:x(n) = w(n) s(n) + v(n)。
其中,表示卷积操作,w(n)表示滤波器的权值。
维纳滤波的目标是设计一个滤波器,使得系统输出信号x(n)与期望输出信号d(n)之间的均方误差最小,即最小化误差信号e(n)的均方值E[e^2(n)]。
根据最小均方误差准则,我们可以得到维纳滤波器的最优解为:w(n) = R_ss^(-1) p_s。
其中,R_ss表示输入信号s(n)的自相关矩阵,p_s表示输入信号s(n)与期望输出信号d(n)的互相关向量。
这个公式描述了维纳滤波器的权值与输入信号和期望输出信号的统计特性之间的关系。
维纳滤波器的设计需要对输入信号和噪声信号的统计特性有一定的了解。
通常情况下,输入信号和噪声信号被假设为高斯分布,因此可以通过它们的均值和方差来描述它们的统计特性。
在实际应用中,我们可以通过对信号和噪声的样本进行统计分析,估计它们的均值和方差,进而设计维纳滤波器。
除了基本的维纳滤波器设计原理,维纳滤波还有一些扩展应用。
例如,当输入信号和噪声信号的统计特性未知或难以估计时,我们可以通过自适应滤波的方法来实现维纳滤波。
自适应滤波器可以根据系统的实时输入信号和输出信号来动态地调整滤波器的权值,以适应信号和噪声的变化特性,从而实现更好的滤波效果。
维纳滤波在图像处理中有着广泛的应用。
在数字图像处理中,图像通常会受到噪声的影响,例如加性高斯噪声、椒盐噪声等。

旋转机械振动信号的小波域维纳滤波去噪杨尚君;张峰;石现峰【摘要】In order to remove the noise in rotating machinery vibration signal during the acquisition and transmission process,the algorithm of Wiener filtering in wavelet domain is proposed to meet the requirements of vibration signal filtering,based on Wiener filtering and wavelet threshold filtering, through the establishment of rotating machinery vibration signal acquisition ing the rotating machinery vibration signal which is actual measurement in the industrial field, the algorithm is simulated.The result shows:This algorithm can maintain the linear phase characteristics for rotating machinery vibration signal,the filtered signal doesn't produce the amplitude distortion;The mean square error of Wiener filtering in wavelet domain is less than that of Wiener filtering and wavelet threshold filtering.The denoising result is better than Wiener filtering and wavelet threshold filtering.%为了去除旋转机械振动信号采集传输过程中混入的噪声干扰,文中基于维纳滤波和小波阈值滤波,通过建立旋转机械振动信号采集模型,结合振动信号滤波要求,提出了旋转机械振动信号的小波域维纳滤波算法.利用工业现场旋转机械实测振动信号,对该算法进行仿真.结果表明:该算法保持了旋转机械振动信号的线性相位特性,滤波后信号未产生明显的幅度失真;小波域维纳滤波的均方误差小于维纳滤波和小波阈值滤波,去噪效果优于维纳滤波和小波阈值滤波.【期刊名称】《西安工业大学学报》【年(卷),期】2016(036)010【总页数】5页(P856-860)【关键词】旋转机械;振动;小波域维纳滤波;线性相位【作者】杨尚君;张峰;石现峰【作者单位】西安工业大学电子信息工程学院,西安 710021;西安工业大学电子信息工程学院,西安 710021;西安工业大学电子信息工程学院,西安 710021【正文语种】中文【中图分类】TN911.4旋转机械故障检测采用数字信号处理的方法对实际测量的振动信号进行分析,用以参数检测和质量评价.在采集及传输的过程中,振动信号不可避免的混入噪声干扰,对振动信号的滤波处理既要取得较好的效果,也要保证振动信号的均衡相位,以便根据这些特性,来进行状态检测和故障诊断,应用于旋转机械振动信号的滤波处理当中.传统的有限冲击响应(Finite Impulse Response,FIR)滤波器和无限冲击响应(Infinite Impulse Response,IIR)滤波器,两者的滤波算法滤波效果和线性相位之间难以达到均衡[1];文献[2]采用维纳滤波对非平稳振动信号进行处理,研究表明未达到预期效果;文献[3]采用循环维纳滤波对振动信号进行周期性的分段处理,每段采用维纳滤波方法,有效的去除了自适应噪声,但是循环维纳滤波算法复杂度大;文献[4]基于离散余弦变换(Discrete Cosine Transform,DCT)算法,保留了信号的部分离散余弦变换域的点数,实现了数据的压缩,但是DCT滤波算法对于大数据的压缩存在着数据丢失,滤波效果差的问题.针对振动信号滤波的敏感相位和滤波效果的问题,文中将维纳滤波和小波阈值滤波相结合,通过建立旋转机械振动信号采集模型,结合振动信号滤波要求,提出旋转机械振动信号的小波域维纳滤波算法.利用工业现场旋转机械实测振动信号,对该算法进行仿真,以期满足滤波要求和线性相位,以适用于其他一维含噪信号的处理.旋转机械振动信号的采集模型如图1所示.图1中ω为旋转机械转轴转动的角频率,v为转轴转动的线速度,理想情况下振动信号可表示为y=A+Bcos(ωt+φ)信号处理前将其直流分量去除,随机变量φ服从在[0,2π]区间的均匀分布,根据平稳随机过程的定义,有E(y)=E[Bcos(ωt+φ)]=Ry(t1,t2)=E[y(t1)y(t2)]=根据工业现场的实际情况,对旋转机械实际振动信号进行实际采集.数据采集的相关参数如下:32倍频采样,采样频率为1 600 Hz,每通道连续采集128点.较为理想情况下,振动信号的时域波形如图2所示.为研究去噪性能,对信号加入非平稳随机噪声,噪声点数为达到与采样点数匹配,故取128点,加噪后的振动信号如图3所示.理想状况下,振动信号各次谐波的谱峰位置应出现在50 Hz的整倍频处,谱峰位置包含了转轴运行状态的有用信息,因此谱峰的准确性直接影响了后期的故障诊断.而初始相位的偏移会导致振动信号后期谱估计中谱峰的分裂或偏移,因此对于振动信号的滤波,单位冲击响应应具有较高的线性相位[5].振动信号频谱图的方差和分辨力性能也直接受到噪声的影响,因此为了获得较好性能的方差和分辨力,应尽可能的对振动信号的噪声进行去除.经典的FIR滤波器和IIR滤波器在滤波效果和线性相位方面均难以满足要求,故需要引入现代的维纳滤波算法来进行处理.根据最小均方误差准则[6],提出一种针对平稳过程的最优估计器.假定观测信号模型为x(n)=s(n)+w(n)式中:s(n)为真实信号;w(n)为加性高斯白噪声,其分布为w(n)~N(0,δ2).根据FIR滤波器准则,有维纳滤波算法原理如图4所示.其中Z-1表示Z变换,e(n)表示真实信号与滤波后信号的误差.均方误差为若使均方误差最小,应满足维纳霍夫方程通过图5可以看出,振动信号的维纳滤波算法保持了信号的初始相位均衡,但滤波效果较差,达不到后期信号处理的要求.根据小波阈值滤波,对含噪声信号进行正交小波变换.选择合适的小波基函数和分解小波层数,对含噪信号进行正交小波分解,得到对应的小波分解系数,其中包含了低频系数和高频系数.选择合适的阈值,对分解后的系数进行阈值处理.每一层小波系数再进行量化处理.进行小波反变换.将阈值处理后的小波系数进行重构,得到小波阈值滤波后的信号.实验选用软阈值函数进行处理[8],数学表达式为δ(σ)=sgn(σ)(|σ|-λ),|ω|>λ根据选用的Coif5小波基,分解2层,小波阈值滤波的结果如图6所示.从图6中可以看出,直接进行小波阈值去噪处理的信号取得了较好的平滑特性,但滤波后信号产生了失真,不能作为后期的信号处理对象.利用Haar小波作为小波基将信号从时域转化为小波域[9].Haar小波基函数为对于非平稳过程,功率谱密度与频率的幂成反比的,振动信号在经小波变换后能够,不同尺度间较强的相关性可有效去除,可以认为非平稳信号在经过小波变换后起到了信号的白化作用[10],满足上述结果的条件须进行正交小波变换,Haar小波作为简单的正交函数,将振动信号从时域转化到小波域选用Haar小波,降低了信号的非平稳特性的同时,保留了信号的有用信息[11-12].根据维纳滤波的原理,在构建维纳霍夫方程前需已知加噪信号和期望信号,利用小波阈值去噪对加噪振动信号进行简单的阈值去噪处理,将原始振动信号作为期望信号,两者同时变换到小波域进行维纳滤波处理[13].小波域维纳滤波算法过程如下:① 将加噪的振动信号进行小波阈值去噪进行预处理,得到信号,用于构建小波域的维纳霍夫方程;② 分别将原始振动信号(作为期望信号)和小波阈值去噪信号两者分别利用Haar小波进行小波变换,分别提取两者的近似分量和细节分量;③ 利用两者细节分量构建维纳霍夫方程,对小波阈值去噪信号的细节分量进行滤波处理,利用两者近似分量构建维纳霍夫方程,对小波阈值去噪信号的近似分量进行滤波处理;④ 利用小波反变换函数对上述信号处理结果进行反变换,其利用的小波基仍为Haar小波.小波域32阶次维纳滤波算法信号处理结果如图7所示.通过图7和图5的对比,小波域维纳滤波算法具有较好的线性相位特性,振动信号初始相位没有发生明显偏移.在小波域维纳滤波的滤波阶数小于维纳滤波阶数的同时,小波域维纳滤波能取得更好的滤波效果.根据图7和图6的比较,利用小波阈值滤波算法保证了振动信号滤波后的平滑特性,该算法可用于实际的振动信号去噪环境中.由于计算量较大,该算法可做振动信号的离线分析处理.分别计算各种算法滤波后的结果与原始振动信号做均方误差的求解,进行算法性能定量分析和对比,得出数据见表1.从表1可看出,小波域维纳滤波的均方误差要小于维纳滤波和小波阈值滤波,小波域维纳滤波算法性能优于各种单独算法,小波域维纳滤波算法滤波后的信号更接近原始的振动信号.利用小波域维纳滤波算法对振动信号进行去噪处理,对其结果进行频谱分析,采取周期图法,功率谱密度(Power Spectral Density,PSD)估计图如图8所示.f为频率,DPS为功率谱密度.根据振动信号的采集模型,信号每周期采样32点,采样频率为1 600 Hz,因此信号的固有频率为50 Hz.从图8中可以看出,滤波后振动信号的谱峰处于50 Hz 整倍频处,功率谱图中的谱峰具有较好的尖锐程度,分辨率性能较好,具有较强辨别信号的能力,且谱峰没有发生偏移或分裂的现象.因此滤波后的振动信号适用于后期的旋转机械故障检测.1) 将振动信号从时域转化到小波域,降低了振动信号的非平稳特性,小波域维纳滤波算法保留了维纳滤波算法的线性相位特性,信号原有的初始相位未发生偏移,滤波后的信号幅值和相位未产生失真.2) 小波域维纳滤波去噪性能优于维纳滤波和小波阈值滤波,均方误差小于维纳滤波和小波阈值滤波.3) 小波域维纳滤波后的振动信号,功率谱图中的谱峰处于50 Hz整倍频处,分辨率性能好,辨别信号的能力优于维纳滤波,谱峰没有发生偏移或分裂,适用于后期的旋转机械故障检测.ZHANG Feng,SHI Xianfeng,ZHANG Xuezhi.Principle and Application of Digital Signal Processing[M].Beijing:Electronics Industry Press,2012.(in Chinese)MING Yang.Study on Cyclostationarity and Blind Source Separation-Based Rolling Element Bearing Fault Feature Extraction[D].Shanghai:Shanghai Jiao Tong University,2013.(in Chinese)MING Yang,CHEN Jin,DONG Guangming.Rolling Bearing Fault Diagnosis Based on Cyclic Wiener Filtering and Envelop Spectrum[J].Journal of Vibration Engineering,2010,23(5):537.(in Chinese)GUAN Bo,HU Jinsong.Research on the Method of the Vibration Signal of Rotating Machinery Based on DCT[J].Turbine Technology,2007,49(4):285. (in Chinese)LI Nan.Study on the Speech Antinoise Based on Wavelet Transform and Wiener Filtering[J].Electro Acoustic Technology,2007,31(5):46.(in Chinese) YANG Lingxiang,YAO Bin.Denoisng Method via Local Wiener Filtering in Wavelet Domain Based on Canny Operator[J].Journal of Bingtuan Education Institute,2009,19(5):35.(in Chinese)LI Dongbing,LI Guoping,TENG Guowei,et al.New Method of De-noising Based on Wavelet and Wiener Filtering[J].VideoEngineering,2013,37(13):26.(in Chinese)HU Yaobin,CHEN Aihua,ZHANG Chunliang.Research of Denoising Technology about Wavelet Analysis with Wiener Filter[J].Communication of Power System,2006,27(162):42.(in Chinese)。



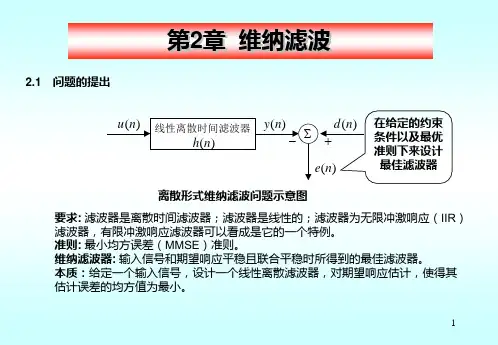
Wiener 滤波概述Wiener 滤波器是从统计意义上的最优滤波,它要求输入信号是宽平稳随机序列,本章主要集中在FIR 结构的Wiener 滤波器的讨论。
由信号当前值与它的各阶延迟({n x )n ,§3.1从估计理论观点导出Wiener 滤波FIR 结构(也称为横向)的Wiener 滤波器的核心结构如图4所示. 图4.横向Wiener 滤波器FIR 结构的Wiener 是一个线性Beyesian 估计问题.为了与第2讲中估计理论一致,假设信号,滤波器权值均为实数由输入)(n x 和它的1至(M-1)阶延迟,估计期望信号)(n d ,确定权系数}1,0,{-=M i w i 使估计误差均方值最小,均方误差定义为:xx R 这里线性0w或a1) 波可能会达到更好结果。
2) 在联合高斯条件下,Wiener 滤波也是总体最优的(①从Bayesian 估计意义上讲是这样,②要满足平稳条件) 3) 从线性贝叶斯估计推导过程知,在滤波器系数取非最优的w 时,其误差性能表示:它是w 的二次曲面,只有一个最小点,0w w =时,m in )(J w J =§3.2维纳滤波:从正交原理和线性滤波观点分析Wiener 滤波器 Wiener 滤波器是一个最优线性滤波器,滤波器核是IIR 或FIR 的。
导出最优滤波器的正交原理,并从正交原理出发重新导出一般IIR 。
=∑∞=--0*)(][k kk n x w n d均方误差是:{}][*][n e n e E J ={}2|][|n e E = 设权系数:k k k jb a w +=定义递度算子Tk ],,[10 ∇∇∇=∇.其中k k k k b ja w ∂∂+∂∂=∂∂=∇符号J ∇是递度算子作用于J ,其中第k 项为:k k k b Jja J J ∂∂+∂∂=∇要求由J 得∇[nje J k由[e a k∂k 代入J k ∇表达式整理得:]][*][[2n e k n x E J k --=∇当0=∇Jk ,1,0=k 时,J 达到最小。

本科毕业设计(论文)题目: 图像去模糊算法对比分析研究学院:专业:班级:学号:学生姓名:指导教师:职称:二○一五年六月一日图像去模糊算法分析与研究摘要在数字时代,图像去模糊作为图像复原技术的一个分支,一直是一个具有挑战和吸引力的问题,具有重大的研究价值与社会意义。
图像去模糊技术近年来得到了广泛研究,在理论和算法上也愈加系统和成熟,根据图像模糊核是否已知,图像去模糊技术被分为非盲图像去模糊和盲图像去模糊两大类。
文章主要是选取几种典型的去模糊算法,在已知模糊核的基础上进行分析研究各算法的特点与去模糊效果的优劣性,即非盲去模糊算法的分析研究。
基于运动模糊和离焦模糊这两大模糊类型,对其分别在有噪声(本文指高斯白噪声)和无噪声情况下的实验结果进行分析比较。
文章首先介绍了两种主要模糊图像类型及其造成图像模糊的成因,并对各模糊类型的点扩散函数估计获取。
其次,是对图像基本退化模型的引入,从本质上了解图像模糊与去模糊的实质。
接着,我们介绍了两类典型的去模糊评价方法:峰值信噪比(Peak Signal to Noise Ratio)和平均结构相似性指数(Mean Structural Similarity Index)。
在这之后主要是算法比较,分类对几种典型的去模糊算法进行数学分析与讨论,包括用于去除运动模糊的Richardson-Lucy算法(即RL算法)和约束最小二乘法;用于去除离焦模糊的逆滤波算法和维纳滤波算法(Wiener filtering)。
最后对几种算法进行Matlab仿真实验设计,并对其结果与恢复效果分析总结。
关键词:离焦模糊;运动模糊;点扩散函数;算法比较;仿真设计AbstractIn digital times,image de—blurring as a branch of image restoration technology has been a hard and attractive problem. However, image restoration has great value of the research and social significance。


去卷积和维纳滤波
去卷积和维纳滤波是两种在图像处理中常用的技术。
去卷积是一种用来提高图像分辨率的技术。
简单来说,它是一种试图从低分辨率图像中恢复原始高分辨率图像的过程。
去卷积的基本原理是利用先验知识(例如噪声分布,傅里叶变换的特性等)来估计模糊函数,然后对模糊后的图像进行反卷积,以得到原始图像的估计。
维纳滤波是一种基于最小均方误差的复原方法,它通过消除图像中的噪声和其他干扰因素来提高图像的质量。
维纳滤波器被设计为对输入图像进行线性变换,以产生输出图像,该输出图像在某种意义上(如均方误差)最接近原始图像。
维纳滤波器通常用于图像的增强和去噪。
在某种程度上,可以认为去卷积和维纳滤波是相关的,因为它们都是用于改善图像质量的工具。
然而,它们的应用领域和目标略有不同。
去卷积主要用于提高图像的分辨率,而维纳滤波则更注重于全局的噪声抑制和图像的全面增强。
维纳滤波器的原理和应用维纳滤波器简介维纳滤波器是一种经典的信号处理滤波器,它基于维纳滤波理论,通过对信号进行统计分析和模型建立,实现信号的优化处理。
维纳滤波器能够降低信号中的噪声成分,提高信号的质量和可靠性,在许多领域中得到广泛的应用。
维纳滤波器原理维纳滤波器的原理是基于最小均方误差的思想,通过最小化信号与噪声之间的均方误差,实现对信号的最优估计。
其数学模型可以表示为:维纳滤波器原理公式维纳滤波器原理公式其中,x(n)是输入信号,h(n)是滤波器的冲激响应,y(n)是滤波器的输出信号,w(n)是噪声信号,E[w(n)w(m)]是噪声信号的自相关函数,Rxx(k)是输入信号的自相关函数,Rxy(k)是输入信号和噪声之间的互相关函数。
维纳滤波器根据输入信号、噪声信号和系统参数的统计特性,通过最小化均方误差优化系统参数,使得滤波器能够有效地抑制噪声成分,提取出原始信号。
维纳滤波器的设计需要基于输入信号和噪声的统计特性的准确估计,以及对滤波器参数的优化求解。
维纳滤波器应用维纳滤波器在实际应用中具有广泛的用途,以下列举了几个常见的应用领域:1.图像去噪:维纳滤波器可以应用于数字图像处理中的去噪问题,通过最小化图像中的噪声与图像信号的误差,实现对图像噪声的抑制,提高图像的质量和清晰度。
2.语音增强:在语音信号处理中,维纳滤波器可以应用于语音增强问题,通过对语音信号进行建模和分析,实现对噪声的抑制,提高语音信号的清晰度和可听性。
3.视频恢复:在视频信号处理中,维纳滤波器可以应用于视频恢复问题,通过对视频帧进行建模和分析,实现对噪声和失真的抑制,提高视频的质量和稳定性。
4.无线通信:在无线通信系统中,维纳滤波器可以应用于信号解调和接收问题,通过对接收信号进行建模和分析,实现对噪声和干扰的抑制,提高信号的可靠性和传输速率。
5.生物信号处理:在生物医学信号处理中,维纳滤波器可以应用于生物信号的去噪和增强问题,通过对生物信号进行建模和分析,实现对噪声和干扰的抑制,提高生物信号的可读性和分析能力。
图像处理中的维纳滤波原理讲解图像处理是计算机视觉领域的重要分支,其中维纳滤波是常用的图像增强技术之一。
本文将详细介绍维纳滤波的原理和应用。
一、维纳滤波的基本概念维纳滤波是一种通过数学推导和图像处理技术实现图像去噪和增强的方法。
它通过分析图像的噪声特征和图像自身的平稳性质,将噪声信号和图像信号进行分离,从而实现图像的清晰化和增强。
在维纳滤波中,首先要了解图像的频谱性质。
图像可以看作是由不同频率的信号叠加而成的,其中高频信号对应于图像的细节信息,而低频信号则对应于图像的整体特征。
维纳滤波的目标就是通过处理图像的频谱进行图像修复和增强,使得图像的细节得到较好的保留。
二、维纳滤波的原理维纳滤波的核心原理是最小均方误差准则,即通过最小化输入信号和输出信号之间的均方误差来实现滤波。
根据此原理,我们可以将维纳滤波分为两个主要步骤:估计噪声功率谱和估计期望图像功率谱。
1. 估计噪声功率谱在维纳滤波中,首先需要估计图像中的噪声功率谱。
为了实现这一步骤,可以使用图像的局部均值作为噪声的估计值,进而计算出噪声的功率谱密度。
2. 估计期望图像功率谱维纳滤波的另一个重要步骤是估计期望图像的功率谱。
期望图像是指在没有噪声的理想情况下所得到的图像。
通过计算图像的自相关函数和噪声的功率谱密度,可以获得期望图像的功率谱。
3. 完成维纳滤波当噪声功率谱和期望图像功率谱都得到估计之后,将它们应用到维纳滤波的公式中,即可完成滤波过程。
维纳滤波器的频谱函数是期望图像功率谱与噪声功率谱的比值。
三、维纳滤波的应用维纳滤波广泛应用于图像处理的许多领域,包括医学图像处理、遥感图像处理、机器视觉等。
以下是维纳滤波常见的应用场景:1. 目标检测与跟踪在目标检测与跟踪中,维纳滤波可以通过增强图像的边缘和细节信息,使得目标更加突出。
维纳滤波可以提高图像的信噪比,减少噪声干扰,使目标的边界更加清晰。
2. 遥感图像处理遥感图像通常受到光照条件和大气扰动的影响,导致图像中存在噪声和模糊。