高三数学复习限时训练1-8

高三数学复习限时训练（17）1、将函数sin(2)3y x π=-的图象先向左平移3π，然后将所得图象上所有的点的横坐标变为原来的2倍（纵坐标不变），则所得到的图象对应的函数解析式为 .2、若]2,0[πθ∈，且54sin =θ，则2tan θ= . 3、两个正数,m n 的等差中项是5，等比中项是4.若m n >，则椭圆221x y m n+=的离心率e 的大小为 .4、以双曲线2213x y -=的一条准线为准线，顶点在原点的抛物线方程是 . 5、已知关于x 的方程1+=ax x 有一个负根，但没有正根，则实数a 的取值范围是6、已知过点O 的直线与函数3x y =的图象交于A 、B 两点，点A 在线段OB 上，过A作y 轴的平行线交函数9x y =的图象于C 点，当BC ∥x 轴，点A 的横坐标是 ；7、等差数列2008200520071,220052007,2008,,}{S S S a n S a n n 则项和是其前中=--=的值为 8、如图，在正方形ABCD 中，E 为AB 的中点，P 为以A 为圆心、AB 为半径的圆弧上的任意一点，设向量AC DE AP λμ=+，则λμ+的最小值为 ；9、 已知函数x x x f cos 26sin 2)(-⎪⎭⎫⎝⎛+=π． （1）当⎥⎦⎤⎢⎣⎡∈ππ,2x 时，若54sin =x ，求函数)(x f 的值； （2）当⎥⎦⎤⎢⎣⎡∈ππ,2x 时，求函数()3sin()cos(2)63h x x x ππ=---的值域；（3）把函数)(x f y =的图象沿X 轴方向平移m 个单位得到函数)(x g 的图象，若函数)(x g 是偶函数，求|m |的最小值．限时训练（17）参考答案1.sin 3y x π⎛⎫=+ ⎪⎝⎭ 2.21 3. 2266y x y x ==-或 5.1≥a 6. 3log 2 7. 2008-8. 129.(Ⅰ) 35．（Ⅱ） 17[,2]8--，(Ⅲ) 3π。

高三数学专题复习 （幂函数）经典1．设⎭⎬⎫⎩⎨⎧--∈3,2,1,21,1,2α，则使幂函数a y x =为奇函数且在(0,)+∞上单调递增的a 值的个数为( )A ．0B ．1C ．2D ．32．设11,0,,1,2,32a ⎧⎫∈-⎨⎬⎩⎭，则使函数ay x =的定义域为R 且为奇函数的所有a 的值有（ ）A ．1个B ．2个C ．3个D ．4个 3．对于幂函数f(x)=45x ，若0＜x 1＜x 2，则12()2x x f +，12()()2f x f x +的大小关系是( )A. 12()2x x f +＞12()()2f x f x + B. 12()2x x f +＜12()()2f x f x + C. 12()2x x f +=12()()2f x f x + D. 无法确定 4．设函数y ＝x 3与21()2x y -=的图像的交点为(x 0，y 0)，则x 0所在的区间是( )A ．(0，1)B ．(1，2)C ．(2，3)D ．(3，4) 5．下列说法正确的是( )A ．幂函数的图像恒过(0,0)点B ．指数函数的图像恒过(1,0)点C ．对数函数的图像恒在y 轴右侧D ．幂函数的图像恒在x 轴上方 6．若0>>n m ，则下列结论正确的是（ ）A. 22m n< B. 22m n <C. n m 22log log >D.11m n> 7．若函数32)32()(-+=m x m x f 是幂函数，则m 的值为（ ）A ．1-B ．0C ．1D ．2 8．幂函数y f x =()的图象经过点142(,)，则(2)f （ ）A.14 B. 12- C. 29．幂函数35m y x -=，其中m N ∈，且在(0,)+∞上是减函数，又()()f x f x -=，则m =（ ）A.0B.1C.2D.310．已知幂函数()mf x x =的图象经过点（4，2），则(16)f =（ ）A.11．已知命题p ：函数2()21(0)f x ax x a =--≠在（0，1）内恰有一个零点；命题q ：函数2ay x -=在(0,)+∞上是减函数，若p 且q ⌝为真命题，则实数a 的取值范围是（ ）A ．1a >B ．a≤2C ． 1<a≤2D ．a≤l 或a>212．[2014·北京西城模拟]已知函数f(x)＝122,0,20x x c x x x ⎧⎪≤≤⎨⎪+-≤<⎩，其中c ＞0.那么f(x)的零点是________；若f(x)的值域是1,24⎡⎤-⎢⎥⎣⎦，则c 的取值范围是________． 13．幂函数()f x x α=经过点P(2,4),则f = .14．设f (x)＝⎪⎩⎪⎨⎧+--21121xx 11>≤x x ，则f [ f (21)]＝15．幂函数 f （x ）=x α（α∈R）过点，则f （4）= ． 16．幂函数 f （x ）=x α（α∈R ）过点，则 f （4）= ． 17．若幂函数y ＝f(x)的图象经过点19,3⎛⎫ ⎪⎝⎭，则f(25)＝________．18．若a ＋a －1＝3，则32a －a －32＝______． 19．若()121a -+<()1232a --,则a 的取值范围是 .20．设函数f (x )＝0102x x x ≥⎨⎛⎫⎪ ⎪⎝⎭⎩，，＜，则f (f (－4))＝________.21．已知幂函数的图像经过点（2，32）则它的解析式是 . 22．已知幂函数()f x x α=在[1,2]上的最大值与最小值的和为5，则α= ． 23．已知幂函数2()(1)mf x m m x =--在(0,)x ∈+∞上单调递减，则实数m = .24．已知幂函数()x f 存在反函数，且反函数()x f 1-过点（2，4），则()x f 的解析式是 . 25．知幂函数13()n y xn N *-=∈ 的定义域为(0,)+∞ ，且单调递减，则n =__________.26．若函数f(x)是幂函数，且满足(4)3(2)f f =，则1()2f 的值为 .27．已知幂函数21()(22)m f x m m x +=-++为偶函数．（1）求()f x 的解析式；（2）若函数()2(1)1y f x a x =--+在区间（2，3）上为单调函数，求实数a 的取值范围．28．已知幂函数y ＝f(x)经过点12,8⎛⎫ ⎪⎝⎭.(1)试求函数解析式；(2)判断函数的奇偶性并写出函数的单调区间．29．已知幂函数y ＝x 3m －9(m∈N *)的图象关于y 轴对称，且在(0，＋∞)上是减函数． (1)求m 的值；(2)求满足不等式(a ＋1)－3m <(3－2a)－3m的实数a 的取值范围． 30．已知二次函数f(x)满足f(2)＝－1,f(－1)＝－1，且f(x)的最大值为8，求二次函数f(x)的解析式．参考答案1．C【来源】2013-2014学年福建省三明一中高二下学期期中考试文科数学试卷（带解析） 【解析】试题分析：因为ay x =是奇函数，所以a 应该为奇数，又在(0,)+∞是单调递增的，所以0a >则只能1,3． 考点：幂函数的性质. 2．B【来源】2014届陕西西工大附中高三上学期第四次适应性训练理数学卷（带解析） 【解析】试题分析：由幂函数的基本性质可知，定义域为R 的a 的值为：{}1,2,3，函数为奇函数的a 的值为{}1,1,3-，故满足条件的所有a 的值为{}1,3两个.考点：幂函数的定义域、奇偶性. 3．A【来源】2013-2014学年江西鹰潭市高一上学期期末考试理科数学试卷（带解析） 【解析】试题分析：可以根据幂函数f(x)＝45x 在（0，+∞）上是增函数，函数的图象是上凸的，则当0＜x1＜x2时，应有12()2x x f +＞12()()2f x f x +，由此可得结论． 考点：函数的性质的应用.4．B【来源】2013-2014学年江西省赣州市六校高一上学期期末联考数学试卷（带解析） 【解析】试题分析：由函数知识知函数y ＝x 3与21()2x y -=的图像的交点为(x 0，y 0)的横坐标x 0即为方程321()2x x -=的解，也是函数函数()f x =321()2x x --的零点，由零点存在性定理及验证法知(1)(2)f f ＜0，故x 0在区间（1,2）内. 由题知x 0是函数()f x =321()2x x --的零点，∵(1)(2)f f =31232211[1()][2()]22----=-7＜0，故选B.考点：函数零点与函数交点的关系，零点存在性定理 5．C【来源】2013-2014学年山东省滕州市高一（上）期末考试数学试家（带解析） 【解析】试题分析：对于A 、D ，幂函数y x α=的图像不一定过点(0,0)，也不一定恒在x 轴的上方，如1y x=不过原点且它的图像也不恒在x 轴的上方，应该是幂函数y x α=的图像恒过定点(1,1)；对于B ，指数函数x y a =恒过定点(0,1)，因为01a =；对于C ，因为对数函数log a y x =（0a >且1a ≠）的定义域为{}|0x x >，所以对数函数的图像恒在y 轴的右侧，故选C.考点：基本初等函数的图像与性质. 6．C【来源】2013-2014学年浙江丽水高一上普通高中教学质量监控数学卷（带解析） 【解析】试题分析：指数函数、对数函数的底数大于 1 时,函数为增函数,反之,为减函数，对于幂函数y x α=而言，当0α>时，在(0,)+∞上递增，当0α<时，在(0,)+∞上递减，而0>>n m ，所以22log log m n >，故选C.考点：1.指数函数；2.对数函数；3.幂函数的性质. 7．A【来源】2013-2014学年甘肃高台第一中学高一秋学期期末考试数学试卷（带解析） 【解析】试题分析：由题意，得231m +=，解得1m =-． 考点：幂函数的解析式． 8．C【来源】2013-2014学年甘肃高台第一中学高一秋学期期末考试数学试卷（带解析） 【解析】试题分析：因为函数的图象y f x =()经过点142(,)，则有142a =，解得2a =-，所以2(2)22f -==． 考点：幂函数的解析式与图象．9．B【来源】2013-2014学年甘肃高台第一中学高一秋学期期末考试数学试卷（带解析） 【解析】试题分析：由题意知350m -<，解得53m <，由()()f x f x -=知函数()f x 为偶函数，又因m N ∈，所以1m =，故选B ．考点：1．幂函数的解析式样 2．幂函数的单调性与奇偶性． 10．B【来源】2013-2014学年甘肃高台第一中学高一秋学期期末考试数学试卷（带解析） 【解析】试题分析：因为幂函数()mf x x =的图象经过点（4，2），所以有24m=，解得12m =，所以(16)4f =． 考点：幂函数解析式与图象． 11．C【来源】2014届宁夏银川一中高三上学期第五次月考理科数学试卷（带解析） 【解析】试题分析：由题知，命题p ：0(1)0a f >⎧⎨>⎩，得1a >，命题q ：20a -<，则2a >，若p 且q ⌝为真命题，则有12a a >⎧⎨≤⎩，故实数a 的取值范围是12a <≤．考点：1、函数的零点；2、幂函数的图象和性质；3、复合命题的真假.12．－1和0 (0,4]【来源】2015数学一轮复习迎战高考：2-4二次函数与幂函数（带解析）【解析】当0≤x≤c 时，由12x ＝0得x ＝0.当－2≤x＜0时，由x 2＋x ＝0，得x ＝－1，所以函数零点为－1和0.当0≤x≤c 时，f(x)＝12x ，所以当－2≤x＜0时，f(x)＝x 2＋x ＝12x ⎛⎫+⎪⎝⎭2－14，所以此时－14≤f(x)≤2.若f(x)的值域是1,24⎡⎤-⎢⎥⎣⎦，即0＜c≤4，即c 的取值范围是(0,4]． 13．2【来源】2013-2014学年广东省顺德市勒流中学高一上学期第2段考数学试卷（带解析） 【解析】试题分析：将P(2,4)点坐标代入幂函数()f x x α=，可得2α=，所以2()f x x =，则2f =.考点：函数的求值. 14．134 【来源】2013-2014学年江苏省扬州中学高二第二学期阶段测试文科数学试卷（带解析） 【解析】试题分析：先从内层算起，23212121-=--=⎪⎭⎫ ⎝⎛f ,13423-11232=⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛-f . 考点：分段函数求值 15．2【来源】2013-2014学年江苏省扬州中学高二第二学期阶段测试文科数学试卷（带解析） 【解析】试题分析：将点()2,2，代入幂函数，得22=α，解得21=α，所以()21x x f =,那么()24421==f考点:幂函数的性质 16．2【来源】2013-2014学年江苏省扬州中学高二第二学期阶段测试理科数学试卷（带解析） 【解析】试题分析：将点()2,2，代入幂函数，得22=α，解得21=α，所以()21x x f =,那么()24421==f考点:幂函数的性质 17．15【来源】2014届高考数学总复习考点引领 技巧点拨第二章第9课时练习卷（带解析） 【解析】设f(x)＝x α，则13＝9α，∴α＝－12，即f(x)＝x －12，f(25)＝1518．±4【来源】2014届高考数学总复习考点引领 技巧点拨第二章第7课时练习卷（带解析）【解析】32a －a －32＝(12a －a －12)(a ＋a －1＋1)．∵(12a －a －12)2＝a ＋a －1－2＝1，∴(12a －a －12)＝±1，∴原式＝(±1)×(3＋1)＝±4. 19．23,32⎛⎫⎪⎝⎭【来源】2014届人教版高考数学文科二轮专题复习提分训练5练习卷（带解析） 【解析】令f(x)=12x-,则f(x)的定义域是{x|x>0},且在(0,+∞)上单调递减,则原不等式等价于10,320,132,a a a a +>⎧⎪->⎨⎪+>-⎩解得23<a<32.20．4【来源】2014年高考数学（文）二轮专题复习与测试选择填空限时训练1练习卷（带解析） 【解析】f (－4)＝12⎛⎫⎪⎝⎭－4＝16， 所以f (f (－4))＝f (16)4 21．5y x =【来源】2013-2014学年贵州遵义湄潭中学高一上学期期末考试数学试卷（带解析）【解析】试题分析：设幂函数方程为ny x =，将点()2,32代入可得322n=，解得5n =，所以此幂函数解析式为5y x =。

高三数学复习限时训练（28）1、定义在区间(－1，1）内的函数f （x )满足2f (x )－f (－x )＝lg (x +1），则f （x )的解析式为 。

2、设函数f (x ）＝01,1)(,)1(lg 112x x f x x x x则若）（>⎩⎨⎧≥<--的取值范围是 . 3、已知2πn x ≠，函数xx 22cos 4sin 1+的最小值是 。

4、设直线3y ax =+与圆222410xy x y +--+=相交于,A B两点，且||=AB ，则=a _________。

5、若函数2()x f x x a =+（0a >）在[)1,+∞则a 的值为6、在等腰直角三角形ABC 中,在斜边AB 上任取一点M ，则AM 〉AC 的概率是7、阅读如图所示的程序框，若输入的n 是100，则输出的变量S 的值是 8、在△OAB中,(2cos ,2sin )OA αα=，(5cos ,OB β=5sin )β,若5OA OB ⋅=-，则OAB S ∆=9、已知在△ABC 中，a 、b 、c 分别为角A B 、C 所对的边,向量(cos ,sin )m A A =,(cos ,sin )n B B =，3sin cos m n B C ⋅=-．（1）求角A 的大小;(2)若a =3，求△ABC 面积的最大值．9、设函数()ln f x ax x =+，()22g x a x =。

（1）当1a =-时，求函数()y f x =图象上的点到直线30x y -+=距 离的最小值;(2）是否存在正实数a ，使()()f x g x ≤对一切正实数x 都成立?若 存在，求出a 的取值范围；若不存在，请说明理由。

限时训练（28）参考答案1、)1lg(31)1lg(32x x -++ 2、（－∞,0)∪(10,+ ∞）3．8 4．0 516．222- 7．5 8。

29、(1)cos cos sin sin m n A B A B ⋅=+, 又3sin cos()m n B A B ⋅=++cos cos sin sin B A B A B =+-，2sin sin B B A = ，sin 2A =,3A π∴=或23A π=．（2）2222cos ab c bc A =+-,①当3A π=时，229bc bc bc +-=≥,1sin 2s bc A ∴==≤②当23A π=时,2293bc bc bc =++≥，故3bc ≤，1sin 2S bc A ∴=≤．9。

高三数学复习课教学设计5篇作为一名老师，时常要开展教学设计的准备工作，教学设计是一个系统设计并实现学习目标的过程，它遵循学习效果最优的原则吗，是课件开发质量高低的关键所在。

教学设计应该怎么写才好呢以下是小编为大家收集的高三数学复习课教学设计，欢迎大家分享。

高三数学复习课教学设计1一、指导思想：以《高中语文教学大纲》和《高考考试说明》为本，全面提高学生语文素养和语文能力，争取20__年高考获取全面胜利。

二、学情分析：7班全班现有41人，经过两年多的高中学习，掌握了一些学习语文的方法，具备一定语文学习能力，但是还有相当一部分学生语文基础知识基本技能不够好，良好的语文学习习惯还没有养成，更有不少同学缺乏应试能力，还有一些同学对语文科学习不够重视，书写潦草，答题不规范。

8班全班现有40余人，多数同学语文基础较差，语文应试能力不高，语文学习积极性不是太高，同学之间语文成绩不平衡，甚至差别很大。

但职高语文考试能力要求不是太高，只要努力，明年高考一定会有好成绩的。

三、考点分析：知识点主要包括以下内容：字音字形,实词虚词，熟语，病句，标点，扩展语句压缩语段，选用仿用变换句式，语言表达准确鲜明生动简明连贯得体，八种修辞方法，名言名句，鉴赏古诗词的形象语言和表达技巧，评价古诗词的思想内容和作者的观点态度，文言实词的含义，文言虚词的意义和用法，文言句式，文言翻译，文言文分析综合，现代文文中重要概念的含义，重要句子的含义，筛选文中信息，分析文章结构把握文章思路，归纳内容要点概括中心意思，概括作者在文中的观点态度，文学类实用类的阅读要具备分析综合鉴赏评价和探究能力，写作能力。

四、具体措施：1. 制定长远的计划及详细的短期计划，做到心中有数，忙而不乱。

2.向45分钟语文课堂教学要质量。

高三学生多数同学把课外时间都给了理化和数学，如何提高语文成绩，只能是向45分钟的语文课堂要效率，在备课时要大量参考多种资料，力求知识的新、全、准。

浅议在高三开展数学小题限时训练的必要性摘要】目前的教育行业中，越来越重视学生的发展，在课堂中以学生为本的理念越来越深入人心。

高三是高中最重要的阶段，教师要结合教学的实际情况有计划的引导学生进行训练，做好课堂教学内容的延伸，利用限时训练提高学生的复习质量。

在开展限时训练时要遵循一定的原则，本文就在高三开展数学小题限时训练的必要性做些分析。

【关键词】高三数学；小题限时训练；必要性分析中图分类号：G623.8 文献标识码：A 文章编号：ISSN1672-2051 （2019）03-002-01引言数学是高考中的重要学科，占据着一定的分值，无论是教师、家长还是学生都对数学比较关注。

但是由于在高中阶段，学生的学习任务比较繁重，特别是到了高三，大多数教师都采用了题海战术来提高学生的学习水平，但训练效果却往往并不尽人意。

这就需要教师能够引导学生开展有效的限时训练，以此来提高学生解决问题的能力。

1、小题限时训练简述我们首先要明确到底什么是小题限时训练：我们所说的小题就是指数学题目中的选择题和填空题，小题在考试中所占的分值比例是非常高的，相对于解答题来说难度又比较小，是需要学生重点把握的部分；限时就是指在进行小题训练的时候，要有一定的时间限制，比如说在15分钟内完成几道填空题或者是几道选择题；训练就是指教师教给学生理论知识，然后让学生在反复的练习中不断的巩固这些知识内容，以提高学生对知识的运用能力，进而取得良好的学习效果。

2、数学限时训练的目的首先，我要强调一下本文所说的限时训练是什么，它是指学生在一定的时间内不依靠课本、其它学习资料及他人帮助的情况下，独立完成练习题的解答。

其次，限时训练的目的主要就是为了使学生通过一定的训练之后能够有效地提高解题的速度、提高反应能力以及思维变通的能力，能够快速地理解题意、准确定位答案，不断地提高学生适应各种考试的能力。

这些能力对于高三的学生来说是非常重要的，是其在高考中能够取得优异成绩的必要条件。

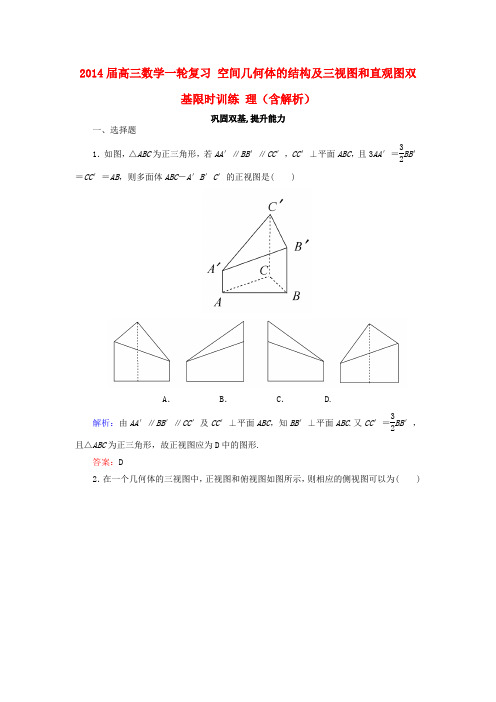
2014届高三数学一轮复习 空间几何体的结构及三视图和直观图双基限时训练 理（含解析）巩固双基,提升能力一、选择题1．如图，△ABC 为正三角形，若AA ′∥BB ′∥CC ′，CC ′⊥平面ABC ，且3AA ′＝32BB ′＝CC ′＝AB ，则多面体ABC －A ′B ′C ′的正视图是( )A ．B ．C ． D.解析：由AA ′∥BB ′∥CC ′及CC ′⊥平面ABC ，知BB ′⊥平面ABC .又CC ′＝32BB ′，且△ABC 为正三角形，故正视图应为D 中的图形.答案：D2．在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )A．B．C．D．解析：由几何体的正视图和俯视图可知，该几何体应为一个半圆锥和一个有一侧面(与半圆锥的轴截面为同一三角形)垂直于底面的三棱锥的组合体，故其侧视图应为D.答案：D3．(2013·枣庄质检)如图，几何体的正视图和侧视图都正确的是( )解析：左视时，看到一个矩形且不能有实对角线，故A、D排除，而正视时，有半个平面是没有的，所以应该有一条实对角线，且其对角线位置应为B中所示，故选B.答案：B4．如图为长方体木块堆成的几何体的三视图，则组成此几何体的长方体木块的块数共有( )A．3块B．4块C．5块D． 6块解析：由几何体的三视图还原出几何体的直观图，如图所示，则可知该几何体是由4块长方体堆放而成的．答案：B5．将长方体截去一个四棱锥，得到的几何体如下图所示，则该几何体的左视图为( )A．B．C． D.解析：根据“长对正，宽相等，高平齐”原则，易知选项D符合题意．答案：D6．(2011·浙江)若某几何体的三视图如图所示，则这个几何体的直观图可以是( )A．B．C． D.解析：所给选项中，A、C选项的正视图、俯视图不符合，D选项的侧视图不符合，只有选项B符合，故选B.答案： B二、填空题7．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的__________．(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱解析：只要判断正视图是不是三角形就行了，画出图形容易知道三棱锥、四棱锥、圆锥一定可以，对于三棱柱，只需要放倒就可以了，所以①②③⑤均符合题目要求．答案：①②③⑤8．如图，在斜二测投影下，四边形ABCD是下底角为45°的等腰梯形，其下底长为5，一腰长为2，则原四边形的面积是__________．解析：作DE ⊥AB 于E ， CF ⊥AB 于F ，则AE ＝BF ＝AD cos45°＝1，∴CD ＝EF ＝3.将原图复原(如图)，则原四边形应为直角梯形，∠A ＝90°，AB ＝5，CD ＝3，AD ＝22，∴S 四边形ABCD ＝12·(5＋3)·22＝8 2.答案：8 29．(2013·广州模拟)已知一个几何体的三视图如下，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是(写出所有正确结论的编号)__________．①矩形②不是矩形的平行四边形；③有三个面为直角三角形，有一个面为等腰三角形的四面体； ④每个面都是等腰三角形的四面体； ⑤每个面都是直角三角形的四面体．解析：由该几何体的三视图可知该几何体是底面边长为a ，高为b 的长方体，这四个顶点的几何形体若是平行四边形，则其一定是矩形.答案：①③④⑤ 三、解答题10．一个正方体内接于高为40 cm ，底面半径为30 cm 的圆锥中，求正方体的棱长． 解析：如图，过正方体的体对角线作圆锥的轴截面，设正方体的棱长为x ，则OC ＝22x ，∴22x 30＝40－x40.解得x ＝120(3－22)．∴正方体的棱长为120(3－22)cm.11．(2011·四平质检)已知正三棱锥V－ABC 的正视图和俯视图如图所示．(1)画出该三棱锥的侧视图和直观图． (2)求出侧视图的面积．解析：(1)如图．(2)根据三视图间的关系可得BC ＝23， ∴侧视图中VA 为42－⎝ ⎛⎭⎪⎫23×32×232＝12＝2 3.∴S △VBC ＝12×23×23＝6.12．如图是一个几何体的正视图和俯视图．(1)试判断该几何体是什么几何体； (2)画出其侧视图，并求该平面图形的面积； (3)求出该几何体的体积． 解析：(1)正六棱锥． (2)其侧视图如图：其中AB ＝AC ，AD ⊥BC ，且BC 的长是俯视图中正六边形对边的距离，即BC ＝3a ，AD 的长是正六棱锥的高，即AD ＝3a ，∴该平面图形的面积S ＝123a ·3a ＝32a 2.(3)V ＝13·6·34a 2·3a ＝32a 3.。

高三数学复习限时训练（42）1、已知集合}1)21(|{},1log |{2≤=<=x x B x x A ，则=⋂B A _______． 2、已知函数()ln 2x f x x =+，若2(2)(3)f x f x +<,则实数x 的取值范围是3、在ABC ∆中，已知),1,2(),2,1(=-=AC AB 则ABC ∆的面积等于4、已知平面,,αβγ,直线,l m 满足：,,,αγγαγβ⊥==⊥m l l m ,那么①m β⊥； ②l α⊥； ③βγ⊥; ④αβ⊥。

可由上述条件可推出的结论有 （请将你认为正确的结论的序号都填上）.5、已知函数()sin 4f x x πω⎛⎫=+ ⎪⎝⎭的图像向左平移6π个单位后与函数()sin 6g x x πω⎛⎫=+ ⎪⎝⎭的图像重合,则正数ω的最小值为6、 设{}n a 是等比数列,公比q =，S n 为{}na 的前n 项和。

记*2117,.n n n n S S T n N a +-=∈设0n T 为数列｛n T }的最大项，则0n =7、已知存在实数a 满足2ab a ab >> ,则实数b 的取值范围为 ． 8、在△ABC 中，π6A ∠=，D 是BC 边上任意一点（D 与B 、C 不重合),且22||||AB AD BD DC =+⋅，则B ∠等于 ．9、。

已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为两切点，求PA PB •的最小值限时训练（42)参考答案1、(0,2）2、 (1，2)3、 254、②④5、2326、 47、(),1-∞-8 、5π129、3。

巩固双基,提升能力一、选择题 1．(2012·辽宁)一排9个座位坐了3个三口之家．若每家人坐在一起，则不同的坐法种数为( ) A．3×3！ B．3×(3！)3 C．(3！)4 D．9! 解析：三个家庭分别在9个座位中挑选3个连排的座位，然后每个家庭中的三个人再分别进行全排列，故坐法种数为A·A·A·A＝(3！)4. 答案：C 2．(2012·浙江)若从1,2,3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有( ) A．60种 B．63种 C．65种 D．66种 解析：要使所取出的4个数的和为偶数，则对取出的数字是奇数或偶数的个数有要求，所以按照取出的数字是奇、偶数的个数分类.1,2,3，…，9这9个整数中有5个奇数，4个偶数．要想同时取4个不同的数其和为偶数，则取法有3类： 4个都是偶数：1种； 2个偶数，2个奇数：CC＝60种； 4个都是奇数：C＝5种． 不同的取法共有66种． 答案：D 3．(2012·安徽)6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品．已知6位同学之间共进行了13次交换，则收到4份纪念品的同学人数为( ) A．1或3 B．1或4 C．2或3 D．2或4 解析：任意两个同学之间交换纪念品共要交换C＝15次，如果都完全交换，每个人都要交换5次，也就是得到5份纪念品，现在6个同学总共交换了13次，少交换了2次，这2次如果不涉及同一个人，则收到4份纪念品的同学有4人；如果涉及同一个人，则收到4份纪念品的同学有2人，答案为D. 答案：D 4．(2012·大纲全国)将字母a，a，b，b，c，c排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有( ) A．12种 B．18种 C．24种 D．36种 解析：利用分步计数原理，先填写最左上角的数，有C＝3种；再填写右上角的数为2种；再填写第二行第一列的数有2种，一共有3×2×2＝12种．故选A. 答案：A 5．(2012·山东)现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张．从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为( ) A．232 B．252 C．472 D．484 解析：由题意可知，抽取的三张卡片可以分为两类，一类为不含红色的卡片，一类是含一张红色的卡片，第一类抽取法的种数为C－3C＝208，第二类抽取法的种数为C·C＝264，故而总的种数为208＋264＝472. 答案：C 6．(2012·课标全国)将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有( )A．12种 B．10种 C．9种 D．8种 解析：因为2名教师和4名学生按要求分成两组共有CC种分法，再分到甲、乙两地有CCA＝12种，所以选A. 答案：A 二、填空题 7．(2013·珠海质检)从5名外语系大学生中选派4名同学参加广州亚运会翻译、交通、礼仪三项义工活动，要求翻译有两人参加，交通和礼仪各有1人参加，则不同的选派方法共有__________种． 解析：本题可分三步完成． 第一步：先从5人中选出2名翻译，共C种选法， 第二步：从剩余3人中选1名交通义工，共C种选法， 第三步：从剩余两人中选1名礼仪义工，共C种选法， 所以不同的选派方法共有CCC＝60(种)． 答案：60 8．(2013·陕西调研)有一个不规则的六面体盒子(六个面大小不同)，现要用红、黄、蓝三种颜色刷盒子的六个面，其中一种颜色刷3个面，一种颜色刷两个面，一种颜色刷1个面，则刷这个六面体盒子的刷法有__________种． 解析：可先分组后分配，即将6个面分成3,2,1三组共有CCC种分组方法，然后每一组用三种颜色去刷，各有A种，由分步计数原理可知共有CCC·A＝360(种)刷法． 答案：360 9．有四位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试，每位同学上、下午各测试一个项目，且不重复．若上午不测“握力”项目，下午不测“台阶”项目，其余项目上、下午都各测试一人，则不同的安排方式共有__________种(用数字作答)． 解析：由题意知，每天只能测八人次，上午不测“握力”，只能从其余四项中任由四人选择，共A＝24种． 下午只测“身高与体重”、“立定跳远”、“肺活量”、“握力”四项，此时按步完成，可先让上午测了“台阶”的人先选一项，若选到“握力”，则另外三人只能从“身高与体重”、“立定跳远”、“肺活量”中选一项，而上午这三项他们又各测过一次，故共有两种选择．若上午测了“台阶”的人，从“身高与体重”、“立定跳远”、“肺活量”中任选一项，有C种选法，比如选到“身高与体重”，此时上午测了“身高与体重”的人可以从“握力”、“立定跳远”、“肺活量”中任选一项，有C种选法，另外两人也就只有一种选择． 故A×(1×C＋C×C)＝24×11＝264(种). 答案：264三、解答题 10．(1)3人坐在有八个座位的一排上，若每人的左右两边都要有空位，则不同坐法的种数有多少种？ (2)有5个人并排站成一排，如果甲必须在乙的右边，则不同的排法有多少种？ (3)现有10个保送上大学的名额，分配给7所学校，每校至少有一个名额，问：名额分配的方法共有多少种？ 解析：(1)由题意知有5个座位都是空的，我们把3个人看成是坐在座位上的人，往5个空座的空当插，由于这5个空座位之间共有4个空，3个人去插，共有A＝24(种)． (2)总的排法数为A＝120(种)，甲在乙的右边的排法数为A＝60(种)． (3)方法一：每个学校至少一个名额，则分去7个，剩余3个名额分到7所学校的方法种数就是要求的分配方法种数． 分类：若3个名额分到一所学校有7种方法； 若分配到2所学校有C×2＝42(种)； 若分配到3所学校有C＝35(种)． 共有7＋42＋35＝84(种)方法．方法二：10个元素之间有9个间隔，要求分成7份，相当于用6块挡板插在9个间隔中，共有C＝84(种)不同方法． 所以名额分配的方法共有84种. 11．用数字0,1,2,3,4,5组成没有重复数字的数： (1)能组成多少个五位数？ (2)能组成多少个正整数？ (3)能组成多少个六位奇数？ (4)能组成多少个能被25整除的四位数？ 解析：(1)因为万位上数字不能是0，所以万位数字的选法有A种，其余四位上的排法有A种，所以共可组成AA＝600(个)五位数．(2)组成的正整数，可以是一位、两位、三位、四位、五位、六位数，相应的排法种数依次为A，AA，AA，AA，AA，AA， 所以可组成A＋AA＋AA＋AA＋AA＋AA＝1 630(个)正整数． (3)首位与个位的位置是特殊位置，0,1,3,5是特殊元素，先选个位数字，有A种不同的选法；再考虑首位，有A种不同的选法，其余四个位置的排法有A种． 所以能组成AAA＝288(个)六位奇数． (4)能被25整除的四位数的特征是最后两位数字是25或50，这两种形式的四位数依次有A·A和A个， 所以，能组成AA＋A＝21(个)能被25整除的四位数.12．(2013·枣庄联考)已知平面αβ，在α内有4个点，在β内有6个点． (1)过这10个点中的3点作一平面，最多可做多少个不同平面？ (2)以这些点为顶点，最多可作多少个三棱锥？ (3)上述三棱锥中最多可以有多少个不同的体积？ 解析：(1)所作出的平面有三类：α内1点，β内2点确定的平面，有C·C个；α内2点，β内1点确定的平面，有C·C个；α，β本身． 所作的平面最多有C·C＋C·C＋2＝98(个)． (2)所作的三棱锥有三类：α内1点，β内3点确定的三棱锥，有C·C个；α内2点，β内2点确定的三棱锥，有C·C个；α内3点，β内1点确定的三棱锥，有C·C个． 最多可作出的三棱锥有C·C＋C·C＋C·C＝194(个)． (3)当等底面积、等高的情况下三棱锥的体积相等，且平面αβ，体积不相同的三棱锥最多有C＋C＋C·C＝114(个)．。

高三文科数学 限时训练卷(5)（福建卷）班次：_______姓名：_________考号：________8 ______－２____________ 9_______131___________ *********************************************************************一、 选择题1．复数的()112i Z i i+=--为虚数单位在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．设点(),,21:10P x y x y P l x y ==-+-=则“且”是“点在直线上”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若集合{}{}=1,2,3=1,3,4A B ⋂，，则A B 的真子集个数为A ．2B ．3C ．4D ．164．双曲线221x y -=的顶点到其渐近线的距离等于A ．12B ．2C ．1D 5．函数()()2ln 1f x x =+的图像大致是6．若变量,x y 满足约束条件21,20,x y x z x y y +≤⎧⎪≥=+⎨⎪≥⎩则的最大值和最小值分别为 A ．43和 B ．42和 C ．32和 D ．20和7．若221,x y x y +=+则的取值范围是A ．[]0,2B ．[]2,0-C ．[2,)-+∞D ．(,2]-∞-二．填空题：８.已知函数()32,0,4tan ,0,2x x f x f f x x ππ⎧<⎛⎫⎪⎛⎫==⎨ ⎪ ⎪-≤<⎝⎭⎝⎭⎪⎩则 . ９.利用计算机产生01,10"a a -<之间的均匀随机数则事件"3发生的概率为 .1０.椭圆2222:1(0)x y r a b a b+=>>的左、右焦点分别为122.F F c 、，焦距为若直线)12212,y x c M MF F MF F =+∠=∠与椭圆r 的一个交点满足则该椭圆的离心率等于 .。

限时训练高三单元滚动卷答案一、语文部分1. 现代文阅读（共30分）第一题（5分）：答案是B。

这题主要考查对文章主旨的理解，从文章第二段中可以找到关键语句，作者提到“这种现象背后的深层次原因是社会价值观的多元”，而选项B准确地概括了这一内容。

第二题（5分）：答案为D。

这是一道关于文章论证方法的题目，文章多处运用了举例论证，如在第三段举了某公司的案例，而选项D所说的对比论证在文章中并没有体现。

第三题（10分）：答案要点如下：首先要概括出文章的中心论点是关于现代社会人们面临多种选择时应如何坚守自我价值。

然后在论述过程中，要提到文章的论证结构是总分总，开头提出问题，中间从不同方面分析，结尾总结观点并给出建议。

第四题（10分）：这是一道开放性题目，答案可以是自己的感悟。

比如可以说在现代社会中，我们要像文中所说的那样，在多元价值的冲击下，坚守自己内心的道德底线，不能随波逐流。

2. 古诗词鉴赏（共20分）第一题（5分）：题目是对古诗中某个字词的理解。

古诗为李白的将进酒中的“君不见黄河之水天上来”中的“来”字。

答案是这个“来”字生动地写出了黄河水奔涌而来的磅礴气势，仿佛是从天上倾泻而下，让读者感受到黄河水的雄浑壮阔。

第二题（5分）：关于古诗的情感赏析。

答案是这首诗表达了诗人李白豁达豪放的情怀，同时也有对时光易逝、人生短暂的感慨。

从诗中的“高堂明镜悲白发，朝如青丝暮成雪”可以看出诗人对时光匆匆的叹息，而后面的“天生我材必有用，千金散尽还复来”又体现出他的豁达。

第三题（10分）：要求对整首诗进行翻译并分析其艺术特色。

翻译：你难道没有看见吗？那黄河之水犹如从天上倾泻而来，波涛翻滚直奔东海，从不回还。

你难道没有看见，在高堂上面对明镜，深沉悲叹那一头白发？早晨还是满头青丝，傍晚却变得如雪一般。

人生得意之时就要尽情地享受欢乐，不要让金杯无酒空对明月。

上天造就了我成材必定会有用，即使散尽黄金，也会重新得到。

煮羊宰牛姑且尽情享乐，今天一次性痛快地饮三百杯也不为多。