金相显微镜不确定度评定细则

结果处理： 合格□准用
□停用□维修□其它
验证人/时间：
批准人/时间：
备注
示值误差的判定：
物镜放大倍数
示值误差△
(%)
MPEV
(%)
MPEV-U
(%)
MPEV+U
(%)
判定
结果
校准证书给出的测量不确定度
Uk=2（%）
5.0
符合
5.0
符合
5.0
符合
校准点（mm）
示值误差△
(μm)
MPEV
(μm)
MPEV-U
(μm)
MPEV+U
(μm)
判定
结果
校准证书给出的测量不确定度
Uk=2（μm）
测量设备计量特性验证记录表
设备名称
金相显微镜
型号规格
设备编号
校准证书号
校准日期
校准间隔
1年
校准单位
校准证书信息量的验证
校准单位符合计量法制的要求，证书给出的信息量完整、正确。
计量特性要求□预期的使用要求
依据JJF 1402-2013生物显微镜校准规范，物镜放大倍数误差不超过±5%，长度测量示值误差不超过10μm。
10.0
符合
10.0
符合
10.0
符合
符合性判断及说明：1.校准给出来自数值范围，满足预期测量范围的要求；
2.如果U≤1/3 MPEV，按判定原则 ≤MPEV符合，则 ＞MPEV判定不符合。如果U＞1/3 MPEV，按判定原则 ≤MPEV-U符合，则 ≥MPEV+U判定不符合,MPEV-U＜ ＜MPEV+U待定。该金相显微镜示值误差符合要求。

浅谈晶粒度测量不确定度评定方法花思明【摘要】晶粒度是晶粒大小的量度，探讨晶粒度测量不确定度的评定方法可以使晶粒度的测量更加准确、可靠。

文中依据YS/T 449-2002的截距法，借助Leica DM2500金相显微镜和JX-2000金相分析软件对铜合金试样的晶粒度进行了测量，并对被测量晶粒度的影响因素进行的分析，进而评定了晶粒度的测量不确定度。

结果表明：与截点个数相比，测量线段的长度对晶粒度的测量不确定度的影响较大；采用该方法可以准确地对测量不确定度进行评定。

%Grain size is a measure of grain size. The discussion on the evaluation method of measurement uncertainty of grain size can make the measurement of the grain size more accurate and reliable. On the basis of YS/T 449-2002 intercept method, by Leica DM2500 optical microscope and JX-2000 metallographic analysis software, this paper measured copper-alloy grain size and analyzed the inlfuencing factors of grain size, then assessed measurement uncertaintyof the grain size. The results showed that:compared with the number ofcut points, the inlfuence of the length of a measuring line is bigger;the method can accurately assess the uncertainty of measurement.【期刊名称】《质量技术监督研究》【年(卷),期】2015(000)002【总页数】4页(P9-11,15)【关键词】晶粒度;测量不确定度;截距法【作者】花思明【作者单位】中铁建电气化局集团康远新材料有限公司，江苏靖江 214500【正文语种】中文（中铁建电气化局集团康远新材料有限公司，江苏靖江 214500）随着当代经济全球化、高新技术的迅猛发展，对各行业实验室检测和校准结果的可靠性要求越来越高，在许多情况下除了要获得检测或校准结果之外，还要求知道检测或校准结果的测量不确定度。

显微镜的不确定度计算公式引言。

显微镜是一种常用的科学仪器，用于观察微小的物体和结构。

在科学研究和实验中，我们经常需要使用显微镜来观察微观世界，并对所观察到的图像进行测量和分析。

然而，由于显微镜的放大倍数和镜头质量等因素的影响，我们在测量过程中会面临一定的不确定度。

因此，了解和计算显微镜的不确定度是非常重要的。

显微镜的不确定度计算公式。

在进行显微镜测量时，我们需要考虑到一些因素，如显微镜的放大倍数、目镜和物镜的焦距、镜头的清晰度等。

这些因素会影响到我们测量的精度和准确度。

为了计算显微镜的不确定度，我们可以使用以下公式：δx = (λf)/m。

其中，δx表示测量结果的不确定度，λ表示光的波长，f表示物镜的焦距，m 表示显微镜的放大倍数。

这个公式是根据显微镜成像的原理推导出来的。

根据光学原理，当光线通过物镜成像时，会产生一定的衍射效应，从而导致成像的模糊和不确定度。

因此，我们可以利用这个公式来计算显微镜测量结果的不确定度。

实际应用。

在实际应用中，我们可以通过以下步骤来计算显微镜的不确定度：1. 确定光的波长。

首先，我们需要确定光的波长。

通常情况下，可见光的波长范围在380nm到780nm之间。

我们可以根据具体的实验条件和光源来确定光的波长。

2. 测量物镜的焦距。

其次，我们需要测量物镜的焦距。

物镜的焦距是显微镜成像的关键参数，直接影响到成像的清晰度和放大倍数。

3. 确定显微镜的放大倍数。

最后，我们需要确定显微镜的放大倍数。

显微镜的放大倍数是通过目镜和物镜的组合来确定的，通常可以通过显微镜的标识或者测量来得到。

通过以上步骤，我们可以得到显微镜测量结果的不确定度。

这个不确定度可以帮助我们评估测量结果的精度和准确度，从而更好地进行科学研究和实验。

总结。

显微镜是一种重要的科学仪器，广泛应用于科学研究和实验中。

在进行显微镜测量时，我们需要考虑到一定的不确定度，以确保测量结果的精度和准确度。

通过使用显微镜的不确定度计算公式，我们可以得到测量结果的不确定度，从而更好地进行科学研究和实验。

金相评级标准(一)金相评级标准1. 引言金相评级标准是对金属材料显微组织进行评级的一种指导性规范。

它主要依据金属材料的显微组织特征，对其进行分类与评估，旨在提供一种客观、统一的标准，以便更准确地描述金属材料的品质和性能。

2. 评级标准概述金相评级标准主要包括以下几个方面：组织形貌•晶粒尺寸：根据晶粒的尺寸大小进行评级，如超细晶、细晶、粗晶等。

•晶粒形状：根据晶粒的形状特征进行评级，如均匀晶、方形晶、柱状晶等。

•相比例：根据相的比例进行评级，如单相、双相、多相等。

组织缺陷•夹杂物：根据夹杂物的种类、分布和形态进行评级，如无夹杂物、少量夹杂物、严重夹杂物等。

•气孔：根据气孔的密度和形态进行评级，如无气孔、少量气孔、密集气孔等。

•裂纹：根据裂纹的长度、宽度和分布进行评级，如无裂纹、小裂纹、大面积裂纹等。

组织性能•硬度：根据金属材料的硬度进行评级，如硬度优良、硬度合格、硬度不合格等。

•强度：根据金属材料的拉伸、屈服等力学性能进行评级，如高强度、一般强度、低强度等。

•韧性：根据金属材料的抗冲击性能进行评级，如优异韧性、普通韧性、脆性等。

3. 评级标准应用金相评级标准广泛应用于金属材料的生产和加工过程中。

它对于金属材料的品质控制、产品检验和质量评估具有重要意义。

以下是评级标准的应用示例：钢材生产•根据金相评级标准对炼钢过程中的组织进行分类与评估，以确保钢材的质量和性能。

•对钢材产品进行金相显微镜下的观察和显微组织分析，判断是否符合金相评级标准要求。

材料研究•通过金相评级标准对不同材料的显微组织特征进行对比和评估，研究其性能差异和影响因素。

•在新材料研发过程中，借助金相评级标准对材料的组织进行分析，为进一步优化材料性能提供参考。

产品质量控制•在金属制品的生产过程中，通过金相评级标准对产品的组织缺陷进行评估，及时发现和解决质量问题。

•对出厂产品进行金相评级标准的检验和测试，确保产品达到规定标准，提高产品质量。

4. 结论金相评级标准作为一种重要的金属材料评估方法，为相关领域的科研、生产和质量控制提供了科学的依据和指导。

生物显微镜物镜示值误差测量结果不确定度评定1 测量方法根据物镜的不同放大倍数，在载物台上放置分度值为0.01mm 的标准玻璃线纹尺，调焦至目镜视场清晰，移动工作台，使目镜中标尺的左端零刻线对准标准玻璃线纹尺零刻线，观察目镜中标尺上被测点的刻线与标准玻璃线纹尺的对应刻线的一致性，在目镜标尺上估读出误差值ΔL 即为显微镜的示值误差。

2 测量模型ΔL =L i -L s式中：ΔL -----测量点的示值误差，mm ；L i -----测量点的标称长度，mm ；L s -----对应测量点的标准线纹尺长度，mm 。

3 方差和灵敏系数考虑各分量彼此独立得：222222c 1i 2s u =u =c u c u L L L ∆••（）（）+（）式中：1c =L ∂∆/i L ∂=1； 2c =L ∂∆/s L ∂=-14 计算分量的标准不确定度4.1 目镜标尺刻线测量时的标准不确定度分量u （L i ）该项不确定度分量包含测量时对零瞄准的影响及相应被测刻线测量时的估读误差两项。

对零瞄准时采用单线瞄准，其其瞄准精度α=60″，其影响最大的是使用5×物镜时，对于10×的目镜，其整体放大倍率为K =50，其瞄准误差为δ=250α／ρK =250×60/2/105/50mm=1.5μm该项瞄准误差主要以均匀分布的方式影响，所以其标准不确定度为u 1（L i ）=δ/相应刻线间隔点测量时，采用观察标准刻线与被测刻线的符合程度确定示值误差，当存在不符合情况时，需要读出被测刻线与标准刻线的间隔量作为示值误差，读数时采用估读的方式，其估读误差为目镜标尺分度的1/10，即1μm ，均匀分布，其不确定度为u 2（L i ）=A/ =1μm/u （L i ）= = 4.2 标准玻璃线纹尺引入的标准不确定度分量u （L s ）所用标准玻璃线纹尺刻线的不确定度由证书可得：U =0.5μm （k =3）u （L s ）=0.50/3=0.17μm由于测量长度在2mm 以内，因此温度影响带来的不确定度在此影响很小，故忽略不计。

不确定度的评定比较完整所采用方法：1、重复性测量引起的不确定度分量1u 评定：① 测量结果最佳估计值x ：∑==ni i x n x 11② 实验标准偏差)(i x s ：∑=--=ni i i x x n x s 12)(11)( ③（实验）标准不确定度1u ：2)(1i x s u = 自由度：11-=n v2、检定装置误差引起的不确定度分量2u 评定：如：0.1级该装置的最大允许误差MPE=±0.1%，则其变化半宽为%1.0=α，在此区间内属均匀分布，因此3=k ，即分量2u ：3%1.02==ku α=0.0577%，该评定信息来源于上级检定证书，因此2u 很可靠，所以自由度为：∞→2v 3、数据修约引起的不确定度分量3u 评定：如：由于0.5S 级电能表的数据化整间距为0.05，半宽区间为a=0.025%，在此区间内属均匀分布，因此3=k ，则 3%025.03==ku α=0.0144%4、标准不确定度u 的计算：232221u u u u ++==22210144.00577.0++u=0.0715%其自由度为：==∑iiv u cu v 44)(μ∞→∞+∞+44440144.00577.090396.00715.0 5、合成标准不确定度c u 的计算：C u u c .==0.0715%×2=0.1430%≈0.14%， 有效自由度：∞→eff v6、扩展不确定度U ：根据JJF 1059.1-2012《测量不确定度的评定与表示》，取包含因子2=k ，则k u U c .==0.0715%×2=0.1430%≈0.14%7、（评定）测量结果报告：=γ-0.044% ±0.14% =U 0.14% 2=k通过以上分析可知，在各不同负载点计算出来的测量不确定度基本上是一样的。

8、验证： 参照JJF1033—2016《计量标准考核规范》公式：∣y 1 - y 2∣≤u u 2221+ 若符合则评定合理则当COS ϕ=1.0 时 |-0.044-(-0.0825) |1.014.022+ ≤1则当COS ϕ=0.5L 时 |0.0135-( 0.0115) |2.018.022+≤1故通过验证可知第九项中测量不确定度的评定结果是合理的。

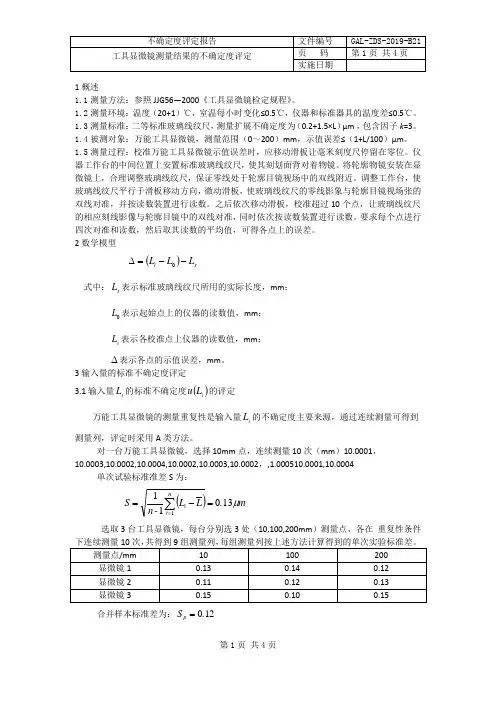
1 概述1.1测量方法：参照JJG56—2000《工具显微镜检定规程》。

1.2测量环境：温度（20+1）℃，室温每小时变化≤0.5℃，仪器和标准器具的温度差≤0.5℃。

1.3测量标准：二等标准玻璃线纹尺，测量扩展不确定度为（0.2+1.5×L ）μm ，包含因子k =3。

1.4被测对象：万能工具显微镜，测量范围（0～200）mm ，示值误差≤（1+L/100）μm 。

1.5测量过程：校准万能工具显微镜示值误差时，应移动滑板让毫米刻度尺停留在零位。

仪器工作台的中间位置上安置标准玻璃线纹尺，使其刻划面背对着物镜。

将轮廓物镜安装在显微镜上，合理调整玻璃线纹尺，保证零线处于轮廓目镜视场中的双线附近。

调整工作台，使玻璃线纹尺平行于滑板移动方向，微动滑板，使玻璃线纹尺的零线影象与轮廓目镜视场张的双线对准，并按读数装置进行读数。

之后依次移动滑板，校准超过10个点，让玻璃线纹尺的相应刻线影像与轮廓目镜中的双线对准，同时依次按读数装置进行读数。

要求每个点进行四次对准和读数，然后取其读数的平均值，可得各点上的误差。

2 数学模型()s i L L L --=∆0式中：s L 表示标准玻璃线纹尺所用的实际长度，mm ； 0L 表示起始点上的仪器的读数值，mm ； i L 表示各校准点上仪器的读数值，mm ； ∆表示各点的示值误差，mm 。

3 输入量的标准不确定度评定3.1 输入量i L 的标准不确定度()i L u 的评定万能工具显微镜的测量重复性是输入量i L 的不确定度主要来源，通过连续测量可得到测量列，评定时采用A 类方法。

对一台万能工具显微镜，选择10mm 点，连续测量10次（mm ）10.0001，10.0003,10.0002,10.0004,10.0002,10.0003,10.0002，,1.000510.0001,10.0004 单次试验标准准差S 为：()m .L L -n S nt i μ130111=-=∑= 选取3台工具显微镜，每台分别选3处（10,100,200mm ）测量点，各在 重复性条件合并样本标准差为：120.S p =实际测量中，渣仔重复条件下连续测量4次，以该4次测量的算数平均值为测量结果则：()m ./S L u p i μ0604==自由度为：()()81110911=-⨯=-=n m v 3.2 输入量0L 引入的标准不确定度()0L u 的评定按3.1测量方法得到：()m .L u 0μ060= 自由度为：()()81110912=-⨯=-=n m v 3.3 输入量s L 引入的标准不确定度()s L u 的评定输入量s L 引入的标准不确定度主要来源有：玻璃刻度尺的定值引入的标准不确定度分量()s1L u ；由于工具显微镜与玻璃刻度尺的温度线膨胀系数引入的不确定度，即当温度偏离标准温度20℃时引入的标准不确定度分量()s2L u ；由于工具显微镜与玻璃刻度尺温度之差引入的标准不确定度分量()s3L u 。

不确定度评定方法
不确定度评定方法是一种通过测量、计算和分析来评定某个量测结果的准确度和可靠性的方法。

在实验中，由于各种因素的影响，量测结果会存在误差，而不确定度评定方法可以帮助我们了解这些误差的大小和来源，从而提高实验的准确性和可靠性。

一般来说，不确定度评定方法包括以下几个步骤：
1. 确定测量的对象和测量方法：首先需要确定所要测量的物理量和使用的测量方法，例如重力加速度的测量可以使用自由落体实验或摆锤实验等方法。

2. 确定影响测量结果的因素：在测量过程中，会有多种因素对测量结果产生影响，包括测量仪器的精度、环境条件的变化、实验者的技能水平等。

需要对这些因素进行分析和评估。

3. 评定各因素的不确定度：通过数据处理和统计分析等方法，可以确定每个因素对测量结果的影响程度，并计算出每个因素的不确定度。

4. 综合不确定度：在确定各因素的不确定度后，需要将其综合起来，计算出整个测量结果的不确定度。

这个过程需要考虑每个因素的权重和相关性等因素。

5. 表达不确定度：最后，需要将不确定度以数值或误差范围的形式表达出来，例如使用标准差、置信区间等指标来表示测量结果的不确定度。

需要注意的是，不确定度评定方法并不是一种万能的解决方案，
它只能帮助我们了解测量误差的大小和来源，而在实际应用中，需要根据具体情况选择合适的评定方法和技术手段。

同时，实验者也需要具备一定的理论知识和实践技能，才能正确地进行测量和不确定度评定。

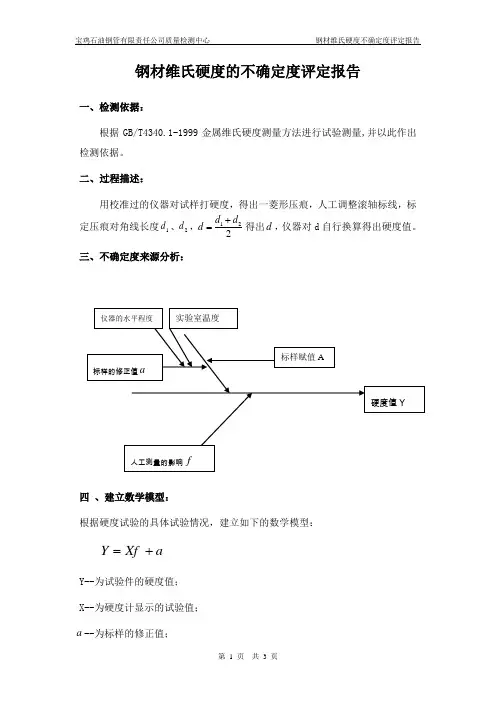
钢材维氏硬度的不确定度评定报告一、检测依据：根据GB/T4340.1-1999金属维氏硬度测量方法进行试验测量,并以此作出检测依据。

二、过程描述：用校准过的仪器对试样打硬度，得出一菱形压痕，人工调整滚轴标线，标定压痕对角线长度1d 、2d ，122d d d +=得出d ，仪器对d 自行换算得出硬度值。

三、不确定度来源分析：四 、建立数学模型：根据硬度试验的具体试验情况，建立如下的数学模型：Y Xf a =+Y--为试验件的硬度值； X--为硬度计显示的试验值；a --为标样的修正值；标样赋值A标样的修正值a硬度值Y人工测量的影响f仪器的水平程度 实验室温度A--标样的赋值；a --对试样硬度测量结果统计获得的平均值；f --人工测量的影响。

五、分析,评定各标准不确定度：1、标准样块的扩展不确定度由检定证书A=223,()0.9%,3,U A A k =⨯=()()0.669U A u A k== 。

2、人工对标样测量十点，各点维式硬度数值a i 如下表： i1 2 3 4 5 6 7 8 9 101d287.3 287.6 287.0 288.0 287.2 287.1 287.5 287.6 287.2 287.32d 288.1 288.1 288.6 288.7 288.6 288.9 288.5 289.0 288.8 288.6d 287.7 287.85 287.8 288.35 287.9 288.0 288.0 288.3 288.0 287.9a i224.0 223.8 223.9 223.0 223.7 223.6 223.6 223.1 223.6 223.710110ik aa ==∑=223.6()u a =1021()(1)in a a m n =--∑=0.29,m=1，n=10；3、取一常规试样,对其十点进行测量，各点维式硬度数值i a 如下表：i 12345678910d 1 282.6289.1286.1285.6285.7284.5286.3285.9288.1286.3d 2 282.0 283.9 281.8 282.5 280.8 282.7 281.4 282.7 282.9 282.9d282.3 286.5 283.9 284.1 283.2 283.6 283.8 284.3 285.5 284.6i a232.7 225.9 230.0 229.8 231.1 230.6 230.2 229.4 227.5 228.910110ii aa ==∑，1021()()(1)ii a a u f m n =-==-∑ 1.75,m=1,n=10，重复性偏差已包含人工测量影响，f=1。

金属材料抗拉强度测量结果的不确定度评定一、 概述1.1 目 的评定金属材料抗拉强度测量结果的不确定度。

1.2 检测依据的标准GB/T228—2010《金属材料 室温拉伸试验方法》。

1.3 检测使用的仪器设备微机控制电子万能试验机，型号：WDW-E100，允差：±1％； 千分尺，型号：0-25mm ，允差：±0.01mm ； 游标卡尺，型号：0-150mm ，允差：±0.02mm 。

1.4 检测程序金属材料的室温拉伸试验抗拉强度检测时，首先根据试样横截面的种类不同测量厚度、宽度或直径，计算截面积S 0；然后用WDW-E100电子拉伸机以规定速率施加拉力，直至试样断裂，读取断裂过程中的最大力F m ，使用R m =F m /S 0计算出抗拉强度(R m )，在同一试验条件下，试验共进行10次。

二、数学模型以矩形横截面金属材料试样为例m m 0m =/=/()R F S F a b (1)式中：R m —抗拉强度，N/mm 2；F m —断裂过程中的最大力，N ； S 0—金属材料横截面积，mm 2； a —金属材料厚度，mm ； b —金属材料宽度，mm 。

三、不确定度来源金属材料抗拉强度R m 测量结果不确定度来源主要包括：(1) 厚度测量重复性引入的标准不确定度u A1，采用A 类方法评定； (2) 千分尺误差引入的标准不确定度u B1，采用B 类方法评定； (3) 宽度测量重复性引入的标准不确定度u A2，采用A 类方法评定；(4) 游标卡尺误差引入的标准不确定度u B2，采用B 类方法评定； (5) 最大力测量重复性引入的标准不确定度u A3，采用A 类方法评定； (6) 拉力机示值误差引入的标准不确定度u B3，采用B 类方法评定； (7) 测量结果数据修约引入的标准不确定度u B4，采用B 类方法评定。

四、标准不确定度评定在同一试验条件下，金属材料抗拉强度R m 检测共进行10次，得到测量列如表1所示：表1 金属材料抗拉强度R m 检测原始数据表1中单次实验标准差使用贝塞尔公式计算：s =金属材料抗拉强度R m 由算术平均值根据式(1)计算给出：5729/1.32*10.54=414.97N/mm 24.1 厚度测量重复性引入的标准不确定度u A1根据表1中厚度检测的单次实验标准差计算结果得到，厚度测量重复性引入的相对标准不确定度u A1=0.0042mm4.2千分尺误差引入的标准不确定度u B1千分尺经上级计量部门检定合格，检定证书给出允差为±0.01mm，区间内服从均匀分布，包含因子k B1a B1=0.01mm，则标准不确定度u B1= a B1/k B1=0.01/3=0.0058mm4.3宽度测量重复性引入的标准不确定度u A2根据表1中宽度检测的单次实验标准差计算结果得到，厚度测量重复性引入的相对标准不确定度u A2=0.0083mm4.4游标卡尺误差引入的标准不确定度u B2游标卡尺经上级计量部门检定合格，检定证书给出允差为±0.02mm，区间内服从均匀分布，包含因子k B2a B2=0.02mm，则标准不确定度u B2= a B2/k B2=0.02/3=0.0116mm4.5最大力测量重复性的不重复引入的标准不确定度u A3根据表1中最大力检测的单次实验标准差计算结果得到，厚度测量重复性引入的相对标准不确定度u A34.6拉力机示值误差引入的标准不确定度u B3拉力机经上级计量部门检定合格，检定证书给出允差为±1%，区间内服从均匀分布，包含因子k B3a B3=1%，则标准不确定度u B3= a B3/k B3=0.01/3=0.00584.7测量结果数据修约引入的标准不确定度u B4根据GB/T228—2010《金属材料室温拉伸试验方法》中规定，对于本例中金属材料抗拉强度R m=414.97 N/mm2时，R m修约到1N/mm2，区间内服从均匀分布，包含因子k B4a B4=1/2=0.5N/mm2，则标准不确定度u B4= a B4/k B4=0.5/3=0.2887N/mm2列表给出不确定度汇总如下：表2 金属材料抗拉强度R m 测量不确定度汇总表五、合成标准不确定度评定对于直接测量，由于各输入量直接互不相关且数学模型中均为乘除关系，所以采用简化方法进行合成合成，如式(2)所示：c =u (2)式中： p i —各输入量的幂指数；r ()i u x —各输入量的相对标准不确定度。

xxx所作业指导书测量不确定度评定Yxxxxxxxxxxxxx 工具显微镜示值误差测量结果20xx-0*-0*批准 20xx-0*-0*实施工具显微镜示值误差测量结果的不确定度评定1.概述1.1测量方法：依据JJG56-2000《工具显微镜检定规程》 1.2环境条件：温度（20±1）℃。

1.3测量标准：标准玻璃线纹尺，扩展不确定度U=0.3μm ，包含因子k=3.0，有效自由度v eff =17。

1.4被测对象：工具显微镜，测量范围为（0~200）mm,最大允许示值误差为2μm 。

1.5测量过程：校准工具显微镜示值误差时，移动滑板使毫米刻度尺处于零位。

将玻璃线纹尺放置在仪器工作台的中间位置上，它的刻划面背着物镜。

在主显微镜上安装轮廓目镜，调整玻璃线纹尺，使其零线处于轮廓目镜视场中的双线附近。

调整工作台，使玻璃线纹尺平行于滑板移动方向，微动滑板，使玻璃线纹尺的零线影像与轮廓目镜视场中的双线对准，并按读数装置进行读数。

然后依次地移动滑板，至少校准10点，使玻璃线纹尺的相应刻线影像与轮廓目镜中的双线对准，并依次地按读数装置进行读数。

每点均应进行4次对准和读数，取其平均值作为该点上的读数，可得各点上的误差。

1.6评定结果的使用：在符合上述条件下的测量结果，一般可直接使用本不确定度的评定结果。

2.数学模型Δ=（L i -L 0 ）- L s 式中：Δ---各点的示值误差L i ----各校准点上仪器的工具值； L 0-------起始点上的仪器的工具值；L s ----标准玻璃线纹尺所用的实际长度。

3.输入量的标准不确定度评定：3.1输入量L i 的不确定度u(L i )的评定输入量L i 的不确定度主要是工具显微镜的测量重复性，可以通过连续测量得到测量列，采用A 类方法进行评定。

对一台工具显微镜，选择10 mm 点，连续测量10次，得到测量列10.0000,10.0002,10.0000,10.0001,10.0002,10.0000,10.0001,10.0000,10.0000,10.0000 mm.s=m n L Li μ08.012=-⎪⎭⎫ ⎝⎛-∑-任意选取3台同类型工具显微镜，每台分别选3处测量点，各在重复性条件下连续测量10次，共得9组测量列，每组测量列分别按上述方法计算得到单次实验标准差，如表--1所示。

生物显微镜测量不确定度的评估1概述1.1 测量依据：JJF （鲁）81-2009《生物显微镜》1.2 计量标准：主要计量标准设备测微分化尺，十字分划目镜。

表1. 实验室的计量标准器和配套设备1.3 测量方法：将十字分划尺置于被校显微镜之载物台上，镜筒内装十字分划目镜，调置到10倍物镜，并对分划尺调焦成像，使分划尺上十字线像与十字分划目镜的竖线（或十字线）重合。

然后转动物镜转换器，向左向右至少三次定位，在目镜分划板上测得分划尺十字像的偏移，以最大偏移值为测定值。

2 数学模型x o =L -L L （1）式中x L —测微分化尺定位前读数，mm ； o L —测微分化尺定位后读数，mm ； 3不确定度传播率式（1）中各分量x L 、o L 相互独立，则有22222c 1x 2o ()()u c u L c u L =+式中，灵敏度系数1x /1c L L =∂∂=，2o /1c L L =∂∂=。

4 标准不确定度评定4.1由测微分化尺真值重复性引入的标准不确定度分量1()u L用A 类评定，在规范要求的环境条件下，用测微分化尺在相同测量条件下对生物显微镜物镜定位准确度连续测量10次，其标准差1L σ10（）=0.007mm ，单次测量标准偏差1L σ1（）0.002=，标准不确定度1()0.002u L =mm 。

4.2 由测微分化尺的准确度引入的标准不确定度2()u L 。

用B 类评定，由测微分化尺的准确度为5µm （k=3），属于正态分布，则2()u L =0.002mm 。

4.3 由测微分化尺分辨力引入的不确定度分量3()u L用B 类评定，显微镜测微尺的最小分度值为0.01mm ，按估读值为其分辨力的1/5，即0.002mm ，则不确定度区间半宽为0.002mL ，按均匀分布计算。

3()u L =0.001mm 4.4 由环境温度和玻璃线膨胀系数差引入的标准不确定度分量可忽略不计。

不确定度评定报告1.测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

2.数学模型 数学模型A=A S +δ式中: A —频率计上显示的频率值 A S —参考频率标准值；δ—被测与参考频标频率的误差。

3.输入量的标准不确定度3.1 标准晶振引入的标准不确定度, 用B 类标准不确定度评定。

标准晶振的频率准确度为±2×10-10, 即当被测频率为10MHz 时, 区间半宽为a ＝10×106×2×10-9＝2×10-2Hz, 在区间内认为是均匀分布, 则标准不确定度为()s A u ＝a/k ＝1.2×10-2Hz()=rel s A u 1.2×10-2/107=1.2×10-93.2被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)u(δ2)来源于被测通用计数器的测量重复性, 可通过连续测量得到测量列, 采用A 类方式进行评定。

对一台通用计数器10MHz 连续测量10次, 得到测量列9999999.6433.9999999.6446.9999999.6448、9999999.6437、9999999.6435.9999999.6428、9999999.6446.9999999.6437、9999999.6457、9999999.6451Hz 。

由测量列计算得算术平均值 ∑==ni i f n f 11=9999999.6442Hz,标准偏差 ()Hz n ffs ni i00091.0121=--=∑=标准不确定度分量u(δ3)=0.00091/=0.00029Hzu(δ3)rel =2.9×10-114 合成标准不确定度评定 主要标准不确定度汇总表不确定度来源（i x ）i a i k ()i u x标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 31.2×10-10 通用计数器引入的标准不确定度分量()1δu2.5×10-2Hz31.5×10-9被测石英晶体振荡器测量重复性()rel u 2δ0.00091Hz 12.9×10-11输入量AS 、δ1.δ2相互独立, 所以合成标准不确定度为u c (A)= 922212105.1)()()(-⨯=++δδu u A u S5 扩展不确定度评定 取k=2, 则 扩展不确定度为U rel ＝k ×u c ＝2×1.5×10-9＝3×10-96测量不确定度报告f ＝f0（1±3×10-9）Hz, k=2不确定度评定报告1.测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

３４计量天地□　李守良　王郁一、概述我们经常接触的是一般普通金相显微镜，它主要用于测量金属表机金相组织的测试，用途比较广泛，对企业和冶金等部门起着实验、研究不可缺少的重要作用。

生产金相显微镜的厂家比效多，型号和规格也不统一，所以对金相显微镜检测至今尚无统一的国家、地方检定规程，因此，依据国家标准对其进行检测。

二、检测项目、方法和技术要求１、物镜转换器定位误差检具：１０倍十字目镜；分划值为０．０１ｍｍ的分划尺，其任意两划线间的极限偏差为０．００５ｍｍ。

检测方法：在被检金相显微镜的转换器上装４０倍物镜，目镜筒内放１０倍十字目镜，对置于载物台上的０．０１ｍｍ分划尺调焦清晰，使分划尺上某一分划与目镜中十字划中心重合，然后转动物镜转换器向左、右多次定位（不少于３次），观察０．０１ｍｍ分划尺像的偏移，以最大偏移值作为检测值。

技术要求：显微镜第一次像的中心最大偏移≤０．０２ｍｍ。

２、转换物镜时第一次像面中心偏差检具：１０倍十字分划目镜和二字分划板。

检测方法：用１０倍十字分划目镜和各放大率物镜在被检显微镜上进行检测，以偏移的最大值作为检测值。

技术要求：由１０倍数物镜转换至其它放大率物镜时均不越出视场。

３、载物台旋转中心偏移检具：１０倍十字分划目镜和二字分划板。

检测方法：在被检金相显微镜上用１０倍十字分划目镜和１０倍物镜对置于载物台上的十字分划板调焦清晰，使十字线中心的像趋向于最小的圆，以最小圆的直径作为检测值。

技术要求：显微镜第一次像的中心最大偏移≤０．２ｍｍ。

４、十字分划目镜的十字线中心偏差检具：十字分划板。

检测方法：在显微镜上用１０倍的物镜和被检十字分划目镜对置于载物台上的十字划板调焦清晰，并使十字分划板中心的像与十字分划板目镜重合，然后旋转十字分划目镜，以两十字线中心的最大偏移作为检测值。

技术要求：十字分划目镜的十字线中心应与目镜升圆轴线重合，其偏差为０．０１ｍｍ。

三、检测中发现的问题显像部分出现的问题比较严重，主要表现在以下三个方面：光学系统：视场模糊或不清晰；成像闪烁，反差不好；转换物镜时不到同焦；即使有高电压，视场也难以鲜明等。

读数、测量显微镜示值误差检定结果不确定度分析 1概述1.1环境条件：温度（20±3）℃。

1.2测量标准：专用玻璃刻度尺1.3被测对象：分度值为0.001mm 读数显微镜，分度值为0.01mm 的测量显微镜1.4测量方法：依照规程中规定的方法1.5评定结果的使用：符合上述条件的测量结果，一般可直接使用本不确定度评定结果。

2数学模型δ=a -L+Δ式中a ——读数显微镜的示值（mm ）L ——专用玻璃刻度尺实际尺寸（mm ）Δ——环境温度和玻璃尺线膨胀系数差引入误差δ——读数显微镜相对于起始点的示值误差3方差和灵敏系数 由上式，有()i n i i c x u x f u 2212∑=⎥⎦⎤⎢⎣⎡∂∂= ()()22322222122∆++==u c u c u c u y u L a c δ式中u a ——读数显微镜示值的标准不确定度分量u L ——专用玻璃刻度尺检定结果的标准不确定度分量u Δ——环境温度和玻璃尺线膨胀系数差引入的标准不确定度分量4计算标准不确定度分量4.1读数显微镜示值的不确定度分量u a读数显微镜15次单向瞄准重复测量实验标准偏差为0.14μm ，由于每点示值误差是4次单向读数的平均值，测量结果以最大与最小示值误差之差来表示，故μm 14.042⨯=a u =0.10μm测量显微镜对同一刻线进行15次重复测量实验标准偏差为1.2μm ，由于示值误差是2次单向读数的平均值，故μm 71.02.0μ01==a u4.2专用玻璃刻度尺检定值引入的标准不确定度分量u L100mm 标准玻璃线纹尺检定结果不确定度为U =0.2μm+1.5L （k =3），则50mm 时31000/505.12.0⨯⨯=L u =0.091μm 8mm 时31000/85.12.0⨯⨯=L u =0.071μm 4.3环境温度和玻璃线膨胀系数差引入的标准不确定度分量u Δ4.3.1由于读数显微镜标尺仅为几毫米，检定用标准玻璃尺在读数显微镜测量范围，受温度影响小，同时读数显微镜标尺和标准玻璃尺均为玻璃材质，其线膨胀系数为10.5×10-6℃-1，故环境温度和玻璃线膨胀系数差引入的标准不确定度分量可忽略不计 u Δ≈04.3.2测量显微镜标尺与玻璃线纹尺线膨胀系数差引入的不确定度u Δ1测量显微镜标尺与玻璃线纹尺的线膨胀系数的测量不确定度在±1×10-6℃-1范围内均匀分布，Δt =2℃，测量长度为50mm 时，u Δ1=50×1000×2×1×10-6/3=0.06μm4.3.2测量显微镜标尺与玻璃线纹尺温度差引入的不确定度u Δ2等温后，测量显微镜标尺与玻璃线纹尺的温度差估计在±1℃范围内均匀分布，则u Δ2=50×1000×10.5×10-6×1/3=0.30μmu Δ2=u Δ12+u Δ22=0.062+0.302u Δ=0.31μm5合成标准不确定度2222∆++=u u u u L a c测量显微镜（0~50）mm 量程0.01mm 分度值 u c ≈0.78（μm ）读数显微镜（0~8）mm 量程0.001mm 分度值u c ≈0.123（μm ）6扩展不确定度取k =2，故测量显微镜（0~50）mm 量程0.01mm 分度值U= ku c =2×0.78≈1.6μm读数显微镜（0~8）mm量程0.001mm分度值U= ku c=2×0.123≈0.25μm 对读数显微镜不同分度值时不确定度计算方法与过程相同，同理可得：0.0025mm分度值读数显微镜U= 0.65μm0.005mm分度值读数显微镜U= 1.3μm0.01mm分度值读数显微镜U= 2.0μm。