不确定度评定案例

测量不确定度案例分析测量不确定度是指测量结果的不确定性范围，它反映了测量过程中的误差以及测量仪器的精度等因素对测量结果的影响。

在科学研究和工程技术领域中，测量不确定度的评估十分重要，可以帮助人们更准确地理解和使用测量结果，并进行可靠的决策。

下面将通过一个案例来分析测量不确定度的应用。

案例：工厂生产电子元器件，为了保证产品的质量，需要对生产线上的电阻进行测量。

工厂购买了一台精度为0.1%的万用表进行测量。

现在需要对其中一批次的电阻进行检测，电阻的理论值为1000欧姆。

解决该问题需要采用合适的测量方法，并评估测量不确定度来确定测量结果的可靠性。

首先，我们需要明确测量方法和条件。

在这个案例中，使用了万用表进行测量，因此需要确定万用表的精度，即0.1%。

另外，还需要确定测量的环境条件，如温度、湿度等。

这些条件对测量结果也会产生影响。

然后，我们需要确定测量结果的不确定度。

在这个案例中，测量结果的不确定度主要包括两个方面：仪器误差和系统误差。

仪器误差是由万用表的精度决定的，即0.1%。

系统误差是由其他因素引起的，如测量环境的影响等。

这些误差可以通过实验来评估。

为了评估系统误差，可以重复多次测量，并计算测量值的标准偏差。

假设进行了10次测量，测量结果如下：1001、1000、999、1002、998、1000、1001、999、1000、1000。

计算这些测量值的标准偏差，可以得到系统误差的估计值。

接下来，需要将仪器误差和系统误差相加得到总误差的估计值。

在这个案例中，仪器误差为0.1%，系统误差的估计值为标准偏差。

因此，总误差的估计值为0.1%+标准偏差。

最后，将总误差的估计值与测量结果相结合，得到最终的测量结果和其不确定度。

在这个案例中，假设次测量结果为1000.5欧姆，根据总误差的估计值，我们可以得到：测量结果：1000.5±（0.1%+标准偏差）欧姆。

通过这个案例，我们可以看到测量结果的不确定度可以帮助确定测量结果的可靠性。

测量不确定度评定的方法以及实例1.标准不确定度方法：U =sqrt(∑(xi-x̅)^2/(n-1))其中，xi表示测量值，x̅表示测量值的平均值，n表示测量次数。

标准不确定度包含随机误差和系统误差等。

例如，对一组长度进行测量，测得的数据为10.2、10.3、10.1、10.2、10.3，计算平均值为10.22，标准差为0.069、则标准不确定度为0.069/√5≈0.031，即U=0.0312.扩展不确定度方法：扩展不确定度是在标准不确定度的基础上，考虑到误差的正态分布，对标准不确定度进行扩展得到的结果，通常以U'表示。

其计算公式如下：U'=kU其中，k表示不确定度的覆盖因子，代表了误差分布的概率密度曲线下的面积，一般取k=2例如，对上述例子中的长度进行测量，标准不确定度为0.031，取k=2，则扩展不确定度为0.031×2=0.062，即U'=0.0623.组合不确定度方法：4.直接测量法：直接测量法是通过多次测量同一物理量，统计测得值的离散程度来评估测量的不确定度。

该方法适用于一些简单的测量，如长度、质量等物理量的测量。

例如，对一些小球的直径进行测量，测得的数据为2.51 cm、2.49 cm、2.52 cm、2.50 cm，计算平均值为2.505 cm，标准差为0.013 cm。

则标准不确定度为0.013/√4≈0.007 cm，即U=0.0075.间接测量法：间接测量法是通过已知物理量之间的数学关系，求解未知物理量的方法来评估测量的不确定度。

该方法适用于一些复杂的测量，如测量速度、加速度等物理量的测量。

例如，测量物体的速度v，则有v=S/t，其中S为位移，t为时间。

若S的不确定度为U_S，t的不确定度为U_t，则根据误差传递法则，计算得到v的不确定度为U_v = sqrt(U_S^2 + (U_t * (∂v/∂t))^2 )。

总之，测量不确定度评定的方法包括标准不确定度方法、扩展不确定度方法、组合不确定度方法、直接测量法和间接测量法。

P245标准不确定度B类评定的举例：（案例1）校准证书上给出标称值为1000g的不锈钢标准砝码质量m s的校准值为1000,000325g，且校准不确定度为24μg（按三倍标准偏差计），求砝码的标准不确定度。

评定：a =U =24μg k=3则砝码的标准不确定度为u B(m s)= 24μg/3 =8μg（案例2）校准证书上说明标称值为10Ω的标准电阻，在23℃时的校准值为10.000074Ω，扩展不确定度为90μΩ，置信水平为99%，求电阻的相对标准不确定度。

评定：由校准证书的信息知道：a =U99=90μΩ，P =0.99；假设为正态分布，查表得到k=2.58；则电阻校准值的标准不确定度为：（JJF1059 b. 被测量Y用扩展不确定度U P给出，而其分布又没有特殊指明时，估计值Y 的分布按正态分布；）u B(R S)=90μΩ/2.58=35μΩ相对标准不确定度为：u B(R S)/ R S=3.5×10-6。

(案例3)手册给出了纯铜在20℃时线热膨胀系数α20(Cu)为16.52×10-6℃-1，并说明此值的误差不超过±0.40×10-6℃-1，求α20(Cu)的标准不确定度。

评定：根据手册，a =0.40×10-6℃-1，依据经验假设为等概率地落在区间内，即均匀分布，查表得，铜的线热膨胀系数的标准不确定度为：u (α20)=0.40×10-6℃-1/ =0.23×10-6℃-1(案例4) 由数字电压表的仪器说明书得知，该电压表的最大允许误差为±（14×10－6×读数+2×10－6×量程），在10 V 量程上测1 V 时，测量10次，其平均值作为测量结果，V = 0.928571 V ，求电压表仪器的标准不确定度。

评定：电压表最大允许误差的模为区间的半宽度：a =(14×10-6×0.928571V +2×10－6×10 V ）=33×10-6 V=33 μV 。

4 不确定度评定举例 （一） 端度规校准1． 概述在比较仪上，对标准端度规和受校准的端度规进行比较，求出两端度规的长度差值，考虑到长度的温度修正，由标准端度规的已知长度，求出受校准端度规的长度。

2． 原理一个名义值50mm 的被校准端度规，将它与同名义长度的已知标准端度规比较，就可求出被校准端度规的长度。

两端度规直接比较的输出是长度差式中：l ：受校端度规在20~C 时的长度；ls ：标准度规在20~C 时的长度(由标准端度规的校准证书给出)： α、αs ：受校与标准规的温度热膨胀系数； θ、θs ：受校与标准规的温度与20℃的温度偏差。

于是：记受校与标准端度规温差sθθδθ-=。

记受校与标准端度热膨胀系数差s ααδα-=则3．不确定度评定：注意到ls ，d ，α，θ，δα，δθ无关，且δα，δθ期望为0。

而于是：(1)标准的校准不确定度校准证书中给出，标准的展伸不确定度U=0.075um ，并说它按包含因子k=3而得，故标准不确定度校准证书指出，它的自由度18)( s l v于是：(2)测量长度差的不确定度测量两规长度差的实验标准差，通过独立重覆观测25次的变化性而得为13nm ，其自由度为25-1=24。

本例比较中，作5次重复观测并采用平均值，平均值的标准不确定度及自由度于是：(3)比较仪偶然效应比较仪检定证书说明，由偶然误差引起的不确定度为0.01um，它由6次重复测量，置水准95％而得，由t分布临界值，t0.95(5)=2.57，故于是：(4)比较仪系统效应比较仪检定证书给出，由系统误差引起的不确定度为0.02um(3水准)，故它可以认为具25%可靠，于是其自由度8%)25(2/1)(2==v d v于是：(5)膨胀系统差的不确定度按均匀分布变化，故它具10％可靠，于是：因(6)规间温差的不确定度标准及被校规应有相同温度，但温差却以等概率落于估计区间-0.05℃至+0.05内任何处，由均匀分布知标准不确定度它具50％可靠，故又不确定度表如下：以上分量无关，合成标准不确定度其自由度在置信水准P=0.99时t0.99(16)=2.92。

不确定度评估实例1、测量问题本次评定实验以物资(商品)检验所游标卡尺09059为测试量具，用游标卡尺测量结构长度270mm的长度ι。

已知卡尺的最大误差为1mm。

用6次测量的平均值作为测量结果。

卡尺的温度效应、弹性效应及其他不确定度来源均忽略不计。

2、数学模型卡尺上得到的读数χ即为测量结果，故得被测长度ι=χ。

但除了读数χ可能引入测量不确定度外，卡尺刻度误差对测量结果也会有影响。

由于卡尺的校准证书未给出其示值误差，因此只能根据其最大允许误差来估计它对测量结果的影响。

若卡尺刻度误差对测量结果的影响διS，则数学模型可以表示为ι=χ+διS式中διS的数学期望值为零，即Ε（διS）=0，但需考虑其不确定度，即μ（διS）≠0。

数学模型是相对的，即使对于同样的被测量，当要求的测量准确度不同时，需要考虑的测量不确定度来源也会有相应的增减，因此数学模型也会不同。

3、测量不确定度分量本测量共有两个不确定度分量，由读数的重复性引入的不确定度μ（χ）和卡尺刻度误差所引起的不确定度μ（διS）。

⑴读数χ的不确定度，μ1（ι）=μ（χ）6次测量结果分别为270、3mm270、1mm270mm271、4mm269、8mm271、2mm则6次测量结果的平均值为==270、47mm平均值的实验标准差为 s()==0、074mm故μ1（ι）=μ()=s()=0、074mm⑵卡尺误差引入的不确定度, μ2（ι）=μ（διS）由于证书未给出卡尺的示值误差,故卡尺刻度误差引入的不确定度由卡尺的最大允许误差得到。

已知卡尺的最大误差为1mm,并以矩形分布估计,于是μ2（ι）=μ（διS）==0、577mm下表给出不确定度分量汇总表符号栏中u1=s1 意为用实验标准s来表示不确定度,言外之意是该不确定度分量有A类评定得到的。

反之，对于未标u=s的不确定度分量，则表示是由B 类评定得到的。

这是经常采用的标明A类评定和B类评定不确定度分量的方法之一。

气相色谱法测定绝缘油溶解气体含量测量不确定度的评定(供参考)一、概述1.1 目的评定绝缘油溶解气体含量测量结果的不确定度。

1.2 依据的技术标准GB/T 17623-1998《绝缘油中溶解气体组分含量的气相色谱测定法》。

1.3 使用的仪器设备(1) 气相色谱分析仪HP5890，经检定合格。

(2) 多功能全自动振荡仪ZHQ701，经检定合格，允差±1℃，分辨力0.1℃。

(3) 经检验合格注射器，在20℃时，体积100mL±0.5mL；体积5mL±0.05mL；体积1mL±0.02mL。

1.4 测量原理气相色谱分析原理是利用样品中各组分，在色谱柱中的气相和固定相之间的分配及吸附系数不同，由载气把绝缘油中溶解气体一氧化碳、二氧化碳、甲烷、乙烷、乙烯、乙炔、氢气带入色谱柱中进行分离，并经过电导和氢火焰检测器进行检测，采用外标法进行定性、定量分析。

1.5 测量程序(1) 校准。

采用国家计量部门授权单位配制的甲烷标准气体。

进样器为1mL玻璃注射器，采用外标气体的绝对校正因子定性分析。

(2) 油样处理。

用100mL玻璃注射器A，取40mL油样并用胶帽密封，并用5mL玻璃注射器向A中注入5mL氮气。

将注入氮气的注射器A放入振荡器中振荡脱气，在50℃下，连续振荡20分钟，静止10分钟。

(3) 油样测试。

然后用5mL玻璃注射器将振荡脱出的气体样品取出，在相同的色谱条件下，进样量与标准甲烷气体相同，对样品进行测定，仪器显示谱图及测量结果。

气体含量测定过程如下。

1.6 不确定度评定结果的应用符合上述条件或十分接近上述条件的同类测量结果，一般可以直接使用本不确定度评定测量结果。

二、 数学模型和不确定度传播律2.1 根据GB/T 17623-1998《绝缘油中溶解气体组分含量的气相色谱测定法》试验方法，绝缘油中溶解气体含量C 的表示式为S s=⨯hC C h μL/L (1) 式中，C ——被测绝缘油中溶解气体甲烷含量，μL/L ；C S ——标准气体中甲烷含量，μL/L ； h ——被测气体中甲烷的峰高A ； h s ——标准气体中甲烷的峰高A 。

汽车侧滑检验台示值误差测量结果的不确定度评定1、 测量方法用检定装置的位移控制装置缓慢推动滑板，使滑板移动，当检定装置的位移测量装置（或百分表）示值为5mm 时，读取侧滑检测仪的仪表示值，按公式（1）计算其示值误差。

2、 测量模型LX X S-=∆ （1） 式中：∆--示值误差，m/km ；X --侧滑检测仪仪表3次示值平均值，m/km ；S X --位移测量装置（或百分表）示值，mm ；L --滑板纵向有效测量长度，m 。

3、 方差和灵敏系数由式（1）得方差：)()()()(2232222212L u c X u c X u c u S c ++=∆ （2）灵敏系数：1)()(1=∂∆∂=X c L X c S 1)()(2-=∂∆∂=23)()(LX L c S =∂∆∂= 4、标准不确定度评定4.1 被检侧滑检测仪引入的标准不确定度被检侧滑检测仪示值的不确定度主要来源于侧滑检测仪的测量结果重复性及数显仪器的分辨力。

由于侧滑检测仪测量重复性引入的标准不确定度与数显仪器的分辨力引入的标准不确定度属于同一种效应导致的不确定度，因此取二者的较大者。

4.1.1测量重复性引入的不确定度测量结果重复性可以通过连续重复测量得到的测量列，采用A 类评定方法进行。

在检定装置的位移测量装置（或百分表）及被检侧滑检测仪正常工作条件下，等精度重复测量10次，数据如下：X =5.03m/km被检侧滑台单次测量实验标准差为：1)(1012--=∑=n X X s i=0.048m/km实际测量时，在重复条件下连续测量3次，以3次测量的算术平均值作为测量结果，则可得侧滑检测仪的测量结果重复性引入的标准不确定度为：()m/km 028.03)(==X s X u A4.1.2被检侧滑台数显分辨力引入的标准不确定度侧滑检测仪的分辨力为0.1m/km ，其量化误差以等概率分布落在宽度为0.05m/km 的区间内，按均匀分布考虑。

至今见过的最规范的不确定度评定的例子!至今见过的最规范的不确定度评定的例子！不确定度是指由于测量误差的存在，对被测量值的不能肯定的程度。

反过来，也表明该结果的可信赖程度。

在报告结果时，必须给出相应的不确定度，一方面便于使用它的人评定其可靠性，另一方面也增强了测量结果之间的可比性。

今天，仪器论坛版友六弦琴为大家找来了不确定度评定的范例，供大家参考。

如有疑问，请点击阅读原文版友将为大家详细解答点击图片查看大图不确定度评定中需要注意的几个问题a)抓住影响测量不确定度主要分量的评估，避免漏项。

通常测量重复性分量、标准物质不确定度分量、工作曲线变动性分量等在合成标准不确定度中所占比重较大，须逐一评估。

对某些不可能进行多次的测定，无重复性数据，应尽可能采用方法精密度参数或以前在该条件下的测试数据进行评估。

b)忽略次要不确定度分量的影响。

有些分量量值较小（属微小不确定度），对合成不确定度的贡献不大。

例如，一个分量为1.0，另一个分量0.33，二者的合成不确定度为1.05，相差5％，即分量0.33在合成标准不确定度中的贡献可忽略。

通常试料称量、相对原子量、物质的摩尔质量等分量相对于测量重复性、工作曲线变动性分量要小得多，一般可忽略。

c)不确定度评估中避免重复评估。

如当已评估了测量重复性分量，不必再评估诸如样品称量、体积测量、仪器读数的重复性分量。

d)不应将一些非输入量的测量条件当作输入量评估。

例如，重量法中高温炉灼烧温度的变动性，测定碳、硫时氧气纯度的变动性，光度分析中波长的精度等，它们不是输入量，其对测量结果的影响反映在测量重复性中，不应将其作为分量进行评估。

e)合成标准不确定度和扩展不确定度通常取一位或两位有效数字。

计算过程中为避免修约产生的误差可多保留一位有效数字。

修约时可采用末位后面的数都进位而不舍去，也可采用一般修约规则。

测量结果和扩展不确定度的数位一致。

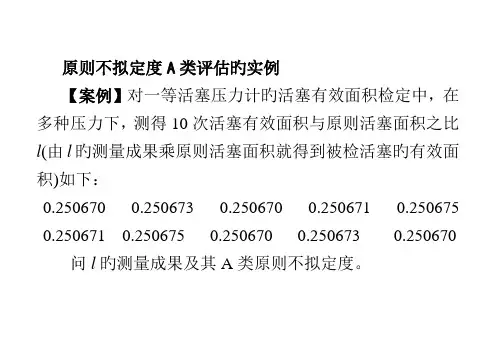
原则不拟定度A类评估旳实例【案例】对一等活塞压力计旳活塞有效面积检定中，在多种压力下，测得10次活塞有效面积与原则活塞面积之比l(由l旳测量成果乘原则活塞面积就得到被检活塞旳有效面积)如下：0.250670 0.250673 0.250670 0.250671 0.250675 0.250671 0.250675 0.250670 0.250673 0.250670问l旳测量成果及其A类原则不拟定度。

【案例分析】由于n =10, l 旳测量成果为l ，计算如下∑===ni i .l n l 125067201由贝塞尔公式求单次测量值旳实验原则差()612100521-=⨯=--=∑.n ll)l (s ni i由于测量成果以10次测量值旳平均值给出，由测量反复性导致旳测量成果l 旳A 类原则不拟定度为610630-=⨯=.)l (u n)l (s A【案例】对某一几何量进行持续4次测量，得到测量值：0.250mm 0.236mm 0.213mm 0.220mm ，求单次测量值旳实验原则差。

【案例分析】由于测量次数较少，用极差法求实验原则差。

)()(i i x u CRx s ==式中，R——反复测量中最大值与最小值之差；极差系数c及自由度ν可查表3-2表3-2极差系数c及自由度ν查表得c n =2.06mm ../mm )..()x (u CR)x (s i i 018006221302500=-=== 2)测量过程旳A 类原则不拟定度评估对一种测量过程或计量原则，如果采用核查原则进行长期核查，使测量过程处在记录控制状态，则该测量过程旳实验原则偏差为合并样本原则偏差S P 。

若每次核查时测量次数n 相似，每次核查时旳样本原则偏差为Si ，共核查k 次，则合并样本原则偏差S P 为ks s ki i p ∑==12此时S P 旳自由度ν=(n -1)k 。

则在此测量过程中，测量成果旳A 类原则不拟定度为n S A P u '=式中旳n '为本次获得测量成果时旳测量次数。

丈量不确立度评定实例一．体积丈量不确立度计算1.丈量方法直接丈量圆柱体的直径 D 和高度 h，由函数关系是计算出圆柱体的体积v D 2 4由分度值为 0.01mm 的测微仪重复 6 次丈量直径 D 和高度 h，测得数据见下表。

表：丈量数据i123456D i / mm10.07510.08510.09510.06510.08510.080 h i / mm10.10510.11510.11510.11010.11010.115计算： D 10.080 mm， h 10.110 mmV D2 h 806.8 mm3 42.不确立度评定剖析丈量方法可知，体积 V 的丈量不确立度影响要素主要有直径和高度的重复丈量惹起的不确立度 u1， u2和测微仪示值偏差惹起的不确立度 u3。

剖析其特色，可知不确立度 u1，u2应采纳A类评定方法，而不确立度 u3采纳B类评定方法。

①.直径 D 的重复性丈量惹起的不确立度重量直径 D 的 6 次丈量均匀值的标准差：s D0.0048 mm直径 D 偏差传达系数：V D hD2直径 D 的重复性丈量惹起的不确立度重量：u1Vs D 0.77mm3 D② .高度 h 的重复性丈量惹起的不确立度重量高度 h 的 6 次丈量均匀值的标准差：s h0.0026 mm高度 h 的偏差传达系数：V D 2h4高度 h 的重复性丈量惹起的不确立度重量：u2Vs h 0.21mm3 h③测微仪示值偏差惹起的不确立度重量由说明书获取测微仪的示值偏差范围0.005mm ，按均匀散布，示值的标准不确立度0.005u q0.00293由示值偏差惹起的直径丈量的不确立度u3D V u qD由示值偏差惹起的高度丈量的不确立度u 3hVhu q由示值偏差惹起的体积丈量的不确立度重量221.04 mm 3u 3u3 Du3h3. 合成不确立度评定u c u 12u 22u 321.3 mm 34. 扩展不确立度评定当置信因子 k 3时，体积丈量的扩展不确立度为Uku c 3 1.3 3.9 mm 35．体积丈量结果报告V V U806.8 3.9 mm 3考虑到有效数字的观点，体积丈量的结果应为V807 4 mm 3二．伏安法电阻丈量不确立度计算1.丈量方法：经过丈量电阻两头电压和所经过的电流，计算被测电阻。

测量不确定度评定示例一、类型1, 有明确的数学模型的经典测量的例子例1. 酸碱滴定不确定度的估计例2. 材料静拉伸强度测定的不确定度估计用1.0级拉力试验机测量圆柱形试件,以受控速率施加轴向拉力，在拉断试件时的静拉伸强度。

在温度和其它条件不变时，拉伸强度可表示为：24πF F A dσ== (1)式中：σ——静拉伸强度，N/mm 2A ——截面积，mm 2 ，对圆柱形试件而言2A=πd /4 d ——圆柱形试件直径，mm F ——拉力，N 由公式（1）有222()()()2c c c u u F u d F d σσ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦…………………………（2） 式（1）和（2）中各量的量值列于表1中。

表1 计算静拉伸强度的不确度的有关量值各量值不确定度的计算：（1）直径d 的测量及其标准不确定度u c (d )用直径计量仪器测定试件的直径为10.00mm 。

其不确定度来源，第一，持证上岗人员多次重复测量的标准偏差经计算为0.005mm ；第二，直径测量仪校准证书上给出在95%置信概率下校准不确定度为0.003mm ，按正态分布转化成标准不确定度为0.003/1.96=0.0015mm以上二项合成有()0.0052mmc ud ==故相对标准不确定度为：()0.00520.0005210.00c ud d==（2）用1.0级拉力试验机测量拉断试件时拉力及其标准不确定度u c (F )。

用1.0级拉力试验机测量拉断试件时拉力为40000N 。

其不确定度来源：第一，示值不确定度对于1.0级拉力试验机供应商说明为示值的±1.0%。

故相对标准不确定度按均匀分布则相对标准不确定度为20.010.5810-=⨯；第二，拉力试验机用0.3级标准测力仪校准，测力仪的相对不确定度为0.3%，按正态分布转化则校准引入的相对标准不确定度为0.003/1.96=0.15×10-2 ;第三，拉力试验机刻度盘量程上限为200kN ，最小分度为0.5kN ，持证上岗人员可估读到0.2分度，即±0.1kN ，本例在40kN 处拉断故±0.1kN/40kN=±2.5×10-3，按均匀分布转化，人员读数引入的相对标准不确定度为332.510 1.410--⨯=⨯，以上三项合成得：() 0.0062c u F F==按公式（2）有：222()0.0062(20.00052)c u σσ⎡⎤=+⨯⎢⎥⎣⎦故2() 3.2/m m c u N σ= 由（1）式有22440000509.3/m mπ10.00N σ⨯==⨯扩展不确定度，取k=2，则2()2 3.2 6.4/mmU N σ=⨯=，取1位有效数字则有2()7/m m U N σ=结果表示为2(5097)/m m N ±。

欢迎阅读测量不确定度评定举例A.3.1 量块的校准通过这个例子说明如何建立数学模型及进行不确定度的评定；并通过此例说明如何将相关的输入量经过适当处理后使输入量间不相关，这样简化了合成标准不确定度的计算。

最后说明对于非线性测量式中：L—被校量块长度；L s—标准量块在20℃时的长度，由标准量块的校准证书给出；?—被校量块的热膨胀系数；?s—标准量块的热膨胀系数；?—被校量块的温度与20℃参考温度的差值；?s —标准量块的温度与20℃参考温度的差值。

在上述测量模型中，由于被校量块与标准量块处于同一温度环境中，所以?与?s 是相关的量；两个量块采用同样的材料，?与?s 也是相关的量。

为避免相关，设被校量块与标准量块的温度差为??，??= ?-?s ；他们的热膨胀系数差为??，??= ?-?s ；将?s = ?-?? 和 ?=??+?s 代入式（A.1），由此，数学模型可改写成：34s 量结果的不确定度没有影响。

合成标准不确定度公式可写成(A.5)：)()()()()(22222222θαδαδθu l u l d u l u l u s s s s c +++= （A.5）4）.标准不确定度分量的评定○1标准量块的校准引入的标准不确定度u (l s )标准量块的校准证书给出：校准值为l s =50.000623mm ，U = 0.075?m (k =3)，有效自由度为?eff (l s )=18。

则标准量块校准引入的标准不确定度为：u (L s )=0.075/3=25nm , ?eff (L s )=18 ○2测得的长度差引入的不确定度u (d ) a. 用对两个量块的长度差进行25次独立重复观测，用贝塞尔公c. 由以上分析得到长度差引入的标准不确定度分量u (d )为： 8.97.85.4)()()(2222=+=+=d u d u d u nm 自由度?eff (d )为：○3膨胀系数差值引入的标准不确定度u (??)估计两个量块的膨胀系数之差在?1×10-6℃-1区间内，假设在区间内为均匀分布，则标准不确定度为： u (??)=1×10-6℃-1/3=0.58×10-6℃-1自由度：估计u (??)的不可靠程度⎦⎤⎢⎣⎡∆)()(ααδδu u 为10%，计算得到?（??）=50%)10(12=- u(△)= 0.5℃/2 =0.35℃ θ的标准不确定度可由下式得到:u(θ)= 41.035.02.0)()(2222=+=∆+u u θ℃ 由于c 4 = c θ=0=-=∂∂θδθs l f, 这个不确定度对l 的不确定度不引入一阶的贡献, 然而它具有二阶贡献.○6 热膨胀系数引入的标准不确定度u (αS ) 标准量块的热膨胀系数给定为αS =11.5×10-6℃-1, 具有一个矩形分布的不确定度,其界限为?2×10-6℃-1, 则标准不确定度为: u (αS )= 2×10-6℃-1/3 = 1.2×10-6℃-1 由于c 3 = c αs =0=-=∂∂θδαs Sl f, 这个不确定度对L 的不确定度不?eff (l )=3.172)6.16(50)9.2(12)8.9(18)25()32(44444=+++ 取?eff (l )=17 6）确定扩展不确定度要求包含概率P 为0.99，由?eff (l )=17，查表得：t0.99(17)=2.90，取k99= t0.99(17)=2.90,扩展不确定度U99= k99u c(l)= 2.90,×32nm=93nm。

开展砝码检定的不确定度评定开展砝码、天平检定的不确定度评定重力式自动装料衡器测量结果的不确定度评估1.概述以一台水泥包装秤为例。

1.1、测量依据：JJG564-2002《重力式自动装料衡器（定量自动衡器）》 1.2、计量标准：主要计量标准设备为M 1等级标准砝码，测量范围（5~20）kg 、100mg~2kg 。

1.4测量方法：先记录下自动装料衡器指示该装料的预设值，然后将每一个装料质量在控制衡器或者控制装置上进行称量，控制衡器（控制装置）的示值作为该装料的约定真值。

2.与装料误差有关的不确定度u(△E) 数学模型：M M M E i /)(-=∆其中：i i i m e I M ∆-+=2/ nMM ni i∑==1式中：M i －第i 次装料质量； M －装料平均值；△m i －第i 次称量时的附加砝码。

不确定度传播率：)()(()()(()(22222M u M c M u M c E u i i +=∆式中：M M M C MM C i i /)(/1)(-==2.1 不确定度分量的评定2.1.1 与装料质量有关的不确定分量u(M) 2.1.1.1由控制衡器分辨率引起的不确定度u 1(M)控制衡器的分度值是20g,由于采用了闪变点法，其分辨率到0.1d ，则:g d m u 58.03/2/1.0)(1==2.1.1.2 与控制示值有关的不确定度分量u 2(M)该分量与控制衡器在该称量点的最大允许误差有关，已知在该称量点的最大允许误差是30g ，服从均匀分布，得：g m u 3.173/30)(2==2.1.1.3 与装料质量有关的不确定分量的合成 )()(()()(()(22222121M u M c M u M c M u +==17.3g 2.1.2 与装料平均值有关的不确定度)(M u数学模型：∑==ni i n M M1/由于称量是在同一控制衡器上进行的，u(Mi)是相同的，故: n M u M u i /)()(=＝3.88g 2.2 与装料误差有关的不确定度u(△E))()(()()(()(2222M u M c M u M c E u i i +=∆=0.0355% 3.与确定准确度等级之一有关的不确定度)(1mpd mdu 数学模型：1max 1/||mpd M M mpd mdi -= 式中： md-最大实际偏差；mpd i - X(1)级最大允许偏差。

附录：测量不确定度评定实例1．用电压表测量稳压电源的输入电压1.1测量方法及测量的数学模型用已经校准的电压表测量一台稳压电源的输出电压U。

电压表的分辨力为0.01V。

电压表校准的不确定度和表的分辨力引起的不确定度可以忽略不计。

因此，多次直接测量，数据的平均值即为输出电压的最佳估计值。

故测量的数学模型可以表示为：U＝U测（1.1）1.2测量数据进行了10次测量，测量数据及相关计算列于表1.1表1.1 输出电压测量数据及相关计算检查平均值和残差的计算是否有误，可将正残差与负残差分别相加，若两个和的绝对值不相等，且两者之差大于末位的1/2，则可判定计算有误。

本例中183i i υυ∑+=∑-=，再复核计算，表明计算正确。

也可直接求残差的代数和看是否为零，或小于末位的半个单位来进行判断。

10次测量值的平均200.56V 10iU U ∑==测 （1.2）即为输出电压U 的最佳估计值。

1.3 根据贝塞尔公式计算测量列的实验标准差，即为单次测量值的实验标准差()()0.477V i S U ==（1.3）S （U i ）表征测量列中测量数据的分散性。

假定测量值服从正态分布，就可以估计，大约有68.3％的测量值处在（200.56±0.48）V 区间内，95％的测量值处在（200.56±2×0.48）V 区间内，99.7％的测量值处在（200.56±3×0.48）V 区间内。

残差绝对值大于3×0.48V 的测量值不应该出现（小概率事件）。

如果出现，可判定为粗大误差。

10次测量的每一个测量值的实验标准差均为0.48V 。

这10个测量值仅是测量值总体的一个样本。

由此计算的标准差仅是这个样本的标准差，而不是总体标准差。

总体标准差可表示为：()i U n σ=→∞（1.4）这无法实际测得，只是理论上存在，又叫理论标准差。

而样本标准差仅是理论标准差的有偏估计值。

测量数据处理及测量不确定度评定案例[案例5]:检查某个标准电阻器的校准证书，该证书上表明标称值为1 MΩ的示值误差为0.001 MΩ，由此给出该电阻的修正值为0.001 MΩ。

案例分析: 该证书上给出的修正值是错误的。

修正值与误差的估计值大小相等而符号相反。

该标准电阻的示值误差为0.001 MΩ，所以该标准电阻标称值的修正值为-0.001 MΩ。

其标准电阻的校准值为标称值加修正值,即：1 MΩ+（-0.001 MΩ）= 0.999 MΩ。

[案例6]：用标准线纹尺检定一台被检投影仪。

在10mm处被检投影仪的最大允许误差为6 μm；标准线纹尺的扩展不确定度为U=0.16μm(k=2)。

用被检投影仪对标准线纹尺的10mm点测量10次，得到测量数据：计算：示值x = x= 9.9988mm ；标准值x s=10mm示值误差= x- x s=9.9988-10=-0.0012mm=-1.2μm示值误差绝对值(1.2μm)小于MPEV（6 μm），由于∣∆∣MPEV，检定结论：合格。

U95/MPEV=0.16/6=1/37.5 ，所用计量标准的不确定度与被检仪器指标之比远小于1/3,满足要求。

因此检定结论可靠。

[案例7]：某法定计量技术机构为要评定被测量Y的测量结果y的合成标准不确定度u c(y)时，y的输入量中，有碳元素C的原子量，通过资料查出C的原子量Ar（C）为：Ar(C）=12.0107±0.0008。

资料说明这是国际纯化学和应用化学联合会给出的值。

如何评定C 的原子量不准引入的标准不确定度分量？案例分析：问题在于：①±0.0008是否是碳元素原子量的不确定度；②如何评定碳元素C的原子量不准引入的标准不确定度分量。

依据JJF1059-1999《测量不确定度的表式和评定》第5节《标准不确定度的B类评定》，①如果对0.0008没有关于不确定度的说明，一般可认为±0.0008不是不确定度，它是允许误差限，也就是Ar(C）=12.0107±0.0008，说明Ar(C）值在（12.0107+0.0008，12.0107-0.0008）区间内，区间半宽度a=0.0008。