《备战2020年高考》2019年高考真题和模拟题分项汇编数学(理)专题11算法初步(解析版)

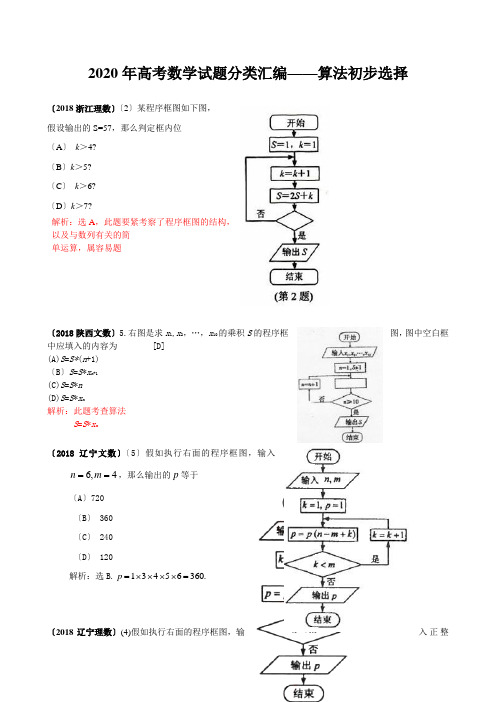
2020年高考数学试题分类汇编——算法初步选择〔2018浙江理数〕〔2〕某程序框图如下图，假设输出的S=57，那么判定框内位〔A〕k＞4?〔B〕k＞5?〔C〕k＞6?〔D〕k＞7?解析：选A，此题要紧考察了程序框图的结构，以及与数列有关的简单运算，属容易题〔2018陕西文数〕5.右图是求x1,x2，…，x10的乘积S的程序框图，图中空白框中应填入的内容为[D](A)S=S*(n+1)〔B〕S=S*x n+1(C)S=S*n(D)S=S*x n解析：此题考查算法S=S*x n〔2018辽宁文数〕〔5〕假如执行右面的程序框图，输入n m==，那么输出的p等于6,4〔A〕720〔B〕 360〔C〕 240〔D〕 120p=⨯⨯⨯⨯=解析：选B.13456360.〔2018辽宁理数〕(4)假如执行右面的程序框图，输入正整数n ，m ，满足n ≥m ，那么输出的P 等于〔A 〕1m n C -(B) 1m n A -(C) m n C(D) m n A【答案】D【命题立意】此题考查了循环结构的程序框图、排列公式，考查了学生的视图能力以及观看、推理的能力【解析】第一次循环：k =1,p =1,p =n -m +1;第二次循环：k =2,p =(n -m +1)(n -m +2)；第三次循环：k =3，p =(n -m +1) (n -m +2) (n -m +3)……第m 次循环：k =3，p =(n -m +1) (n -m +2) (n -m +3)…(n -1)n现在终止循环，输出p =(n -m +1) (n -m +2) (n -m +3)…(n -1)n =m n A〔2018浙江文数〕4.某程序框图所示，假设输出的S=57，那么判定框内为(A) k >4? (B) k >5?(C) k >6? (D) k >7?解析：选A ，此题要紧考察了程序框图的结构，以及与数列有关的简单运算，属容易题〔2018天津文数〕(3)阅读右边的程序框图，运行相应的程序，那么输出s 的值为(A)-1 (B)0 (C)1 (D)3【答案】B【解析】 此题要紧考查条件语句与循环语句的差不多应用，属于容易题。

专题08数列1．【2019年高考全国I卷理数】记S为等差数列n {a}n的前n项和．已知S 0，a 545，则A．a 2n 5n B．a 3n 10nC．S 2n28nnD．Sn 12n22n【答案】A【解析】由题知，dS 4a 430a 32，解得，∴d 2a a 4d 551a 2n 5，S nn n24n,故选A．【名师点睛】本题主要考查等差数列通项公式与前n 项和公式，渗透方程思想与数学计算等素养．利用等差数列通项公式与前n 项公式即可列出关于首项与公差的方程，解出首项与公差，再适当计算即可做了判断．2．【2019年高考全国III卷理数】已知各项均为正数的等比数列a的前4项和为15，且na53a 4a31，则a3A．16 C．4【答案】C B．8 D．2【解析】设正数的等比数列{a}的公比为，则a 1,4，故选C．2解得，a a q31a a q a q2a q1111a q43a q24a111315，【名师点睛】本题利用方程思想求解数列的基本量，熟练应用公式是解题的关键. 3．【2019年高考浙江卷】设a，b∈R，数列{a }满足a=a，a=a+b，n N ，则A．当b 12,a 1010B．当b14,a 1010C．当b 2,a 1010D．当b 4,a 1010【答案】A【解析】①当b=0时，取a=0，则a 0,n Nn .141qn1q 22n n+1n11②当b<0时，令x x2b，即x2x b 0.则该方程14b 0，即必存在x，使得x200x b 0 0，则一定存在a=a=x，使得a10n 1a2nb a对任意n N 成立，n解方程a2a b 0，得a 114b2，当114b114b10时，即b …90 时，总存在a22，使得a a a 101210，故C、D两项均不正确.③当b 0时，a a221b b，则a a2b b2b32，a a2b …b 2b 2b.43111117（ⅰ）当b 时a 1,a 1 22221612，则1111a12224，a 2 721922，9183a 10224，则a a2981210，a a21091210，故A项正确.（ⅱ）当b 14时，令1111 a=a=0，则a ,a4442，所以所以1111a a242421111a a24242，以此类推，，222，45262821232432109故B项不正确.故本题正确答案为A.【名师点睛】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进一步讨论的可能取值，利用“排除法”求解.4．【2019年高考全国I121【答案】3卷理数】记S为等比数列{a}的前n项和．若n n1a ，a2a3，则S=____________．5【解析】设等比数列的公比为，由已知a1111,a a，所以(q)q3335,又q 0，所以q 3,所以S51(135)a (1q5)12111q133．【名师点睛】准确计算，是解答此类问题的基本要求．本题由于涉及幂的乘方运算、繁分式的计算，部分考生易出现运算错误．5．【2019年高考全国III卷理数】记S为等差数列{a}的前n项和，a≠0，a 3an n121，则S10S5___________.【答案】4【解析】设等差数列{a }的公差为d,n因a 3a，所以a d 3a，即2a d 21111，所以S10S510a15a1109d254d2100a1425a1．【名师点睛】本题主要考查等差数列的性质、基本量的计算．渗透了数学运算素养．使用转化思想得出答案．6．【2019年高考北京卷理数】设等差数列{a}的前n项和为S，若a=−3，S=−10，则a=__________，Sn n255的最小值为__________．n 【答案】0，10.【解析】等差数列an 中,S55a 10,得a 2,又a 3332,所以公差d a a 132,a a 2d 0 53,由等差数列an 的性质得n 5时,a 0a146q232463n,n 6时,an 大于0,所以S的最小值为S或S,n45即为10.3【名师点睛】本题考查等差数列的通项公式､求和公式､等差数列的性质,难度不大,注重重要知识､基础知 识､基本运算能力的考查.7．【2019 年高考江苏卷】已知数列{a }(n N n* )是等差数列， S是其前 n 项和. n若a aa0, S27 2 589，则 S 的值是_____.8【答案】16a aa a da 4da 7d 02581 11【解析】由题意可得：9 8S 9a d 272，解得：a5 1 d2，则S 8a 81872d 40 28 2 16.【名师点睛】等差数列、等比数列的基本计算问题，是高考必考内容，解题过程中要注意应用函数方程思想，灵活应用通项公式、求和公式等，构建方程（组），如本题，从已知出发，构建a ,d 1的方程组.8．【2019 年高考全国 II4b3b a 4 .n nn 1卷理数】已知数列{a }和{b }满足 a =1，b =0， n n 1 14a 3ab4 n 1nn，（I ）证明：{a +b }是等比数列，{a –b }是等差数列；n n n n（II ）求{a }和{b }的通项公式.n n【答案】（I ）见解析；（2）an11 1 1 n ， b n2n2 2n2.【解析】（1）由题设得4(a b ) 2(ab ) n 1n 1nn，即an 1bn 11 2(ab ) nn．又因为a +b =l ，所以1 1a bnn是首项为1，公比为1 2的等比数列．由题设得4(ab ) 4(ab ) 8 ，即 abab2 n 1n 1 n nn 1n 1nn．又因为a –b =l ，所以1 1a b nn是首项为1，公差为2的等差数列．（2）由（1）知，abnn12n 1，a b 2n1 n n．所以an1 1 1 [(a b ) (ab )]n22n2，9 1n nn nn4111b [(a b )(a b )]n ．22n29．【2019年高考北京卷理数】已知数列{a }，从中选取第in1项、第i2项、…、第i项（i<i<…<i m12m），若a aa ii i1 2 m ，则称新数列a，a ，，a ii i1 2 m为{a}的长度为m的递增子列．规定：数列{a}的任意nn一项都是{a}的长度为1的递增子列．n（Ⅰ）写出数列1，8，3，7，5，6，9的一个长度为4 的递增子列；（Ⅱ）已知数列{a }的长度为p的递增子列的末项的最小值为a，长度为q的递增子列的末项的最小值n m为a．若p<q，求证：n0a<a；m n0 0（Ⅲ）设无穷数列{a}的各项均为正整数，且任意两项均不相等．若{a }的长度为s的递增子列末项的最n n小值为2s–1，且长度为s末项为2s–1的递增子列恰有2个（s=1，2，…），求数列{a }的通项公式．n【答案】(Ⅰ)1,3,5,6（答案不唯一）；(Ⅱ)见解析；(Ⅲ)见解析.【解析】（Ⅰ）1，3，5，6.（答案不唯一）（Ⅱ）设长度为q末项为a的一个递增子列为na a a由p<q，得.r r np q 1 0a,a,r r1 2,arq1,an.因为an 的长度为p的递增子列末项的最小值为am，又a,a,r r1 2,arp是a的长度为p的递增子列，n所以am0arp.所以am0an·（Ⅲ）由题设知，所有正奇数都是an中的项.先证明：若2m是an中的项，则2m必排在2m−1之前（m为正整数）.假设2m排在2m−1之后.设a,a,,ap p1 2pm1,2m 1是数列an的长度为m末项为2m−1的递增子列，则a,a,,ap p 1 2pm1,2m 1,2m是数列a的长度为m+1末项为2m的递增子列.与已知矛盾.n再证明：所有正偶数都是ann n n n ns-1中的项.假设存在正偶数不是an 中的项，设不在an中的最小的正偶数为2m.5因为2k 排在2k −1之前（k =1，2，…，m −1），所以2k 和2k1不可能在an的同一个递增子列中.又an中不超过2m +1的数为1，2，…，2m −2，2m −1，2m +1，所以an的长度为m+1且末项为2m+1的递增子列个数至多为 2 2 22 112m 1 2m. ( m 1)个与已知矛盾.最后证明：2m 排在2m −3之后（m ≥2为整数）.于 假设存在2m （m ≥2），使得2m 排在2m −3之前，则2 m .与已知矛盾. an的长度为m +1且末项为2m +l 的递增子列的个数小综上，数列an只可能为2，1，4，3，…，2m −3，2m ，2m −1，….经验证，数列2，1，4，3，…，2m −3，2m ，2m −1，…符合条件.所以n 1,n 为奇数， an 1,n 为偶数.【名师点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解 .但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变 应万变才是制胜法宝.10．【2019 年高考天津卷理数】设an是等差数列，bn是等比数列．已知a4, b6 ，b2a2, b2a4 1122 33．（Ⅰ）求an和bn的通项公式；1, 2kn 2k 1, （Ⅱ）设数列 c 满足 c 1,cb , n 2k ,k（i ）求数列ac 1的通项公式；22其中 k N *．（ii ）求a c i in N *．i 1【答案】（Ⅰ）a3n 1 n；b3 2nn（Ⅱ）（i ） a2n c 194n 12（ii ）n1nnnn2n n2na cn N * n N *272i i2n 152n 1n 12i 16【解析】（Ⅰ）设等差数列a的公差为d ，等比数列b的公比为q nn．依题意得6q 6 2d , 6q 2 12 4d ,解d 3, 得 故 a 4 (n 1) 3 3n 1, b 6 2 q 2,n13 2n ．所以，an的通项公式为an3n 1,b的通项公式为 bnn3 2n ．（Ⅱ）（i ） a 2所以，数列an c 1a b 132n 132n 194nn nc 1的通项公式为ac 194n 1．n1．2n 2n 2n 2n（ii ）a c a a c 1aa ci i iiiiiii 1i 1i 1i 112n 2n 1 n2n 4 3 9 4i 1 2 i 1322 n 15 2n 194 14n14n27 22 n 1 5 2n 1 n 12n N *．【名师点睛】本小题主要考查等差数列、等比数列的通项公式及其前 n 项和公式等基础知识．考查化 归与转化思想和数列求和的基本方法以及运算求解能力．11．【2019 年高考江苏卷】定义首项为 1 且公比为正数的等比数列为“M －数列”.（1）已知等比数列{a } n(n N )满足：a a a , a4a4a0 2 45321，求证:数列{a }为“M －数列”；n（2）已知数列{b } n(nN )满足:b1, 11 2 2Sb b nnn 1，其中 S 为数列{b }的前 n 项和． n n①求数列{b }的通项公式；n②设 m 为正整数，若存在“M －数列”{c } n(n N )，对任意正整数 k ，当 k ≤m 时，都有c 剟b c k k k 1成立，求 m 的最大值．【答案】（1）见解析；（2）①b =nn N *；②5.n【解析】解：（1）设等比数列{a }的公比为q ，所以a ≠0，q ≠0.nn22222nnn n2211n1由a a a245a 4a 4a 0321a2q4，得a q21a q414a q 4a 011a 1，解得．q 27因此数列{a}n为“M—数列”.122（2）①因为，所以S b bn n n 1b 0 n．由b 1,S b111，得12211b2，则b 22.122b b由，得S ，S b b2(b b )n n n 1n 1n当n 2时，由b S Sn n n 1，得bnb b b bn n 1n 1n2b b2b b n1n n n 1，整理得b b 2bn 1n 1n．所以数列{b}是首项和公差均为1的等差数列.n因此，数列{b }的通项公式为b=nn n.②由①知，b=k，k N*nN*因为数列{c}为“M–数列”，设公比为q，所以c=1，q>0.n1因为c≤b≤c kk k+1，所以q k 1k q k，其中k=1，2，3，…，m.当k=1时，有q≥1；当k=2，3，…，m时，有ln k ln kln qk k 1．设f（x）=ln x1ln x (x 1)，则f'(x)x x2．令f'(x)0，得x=e.列表如下：因为x(1,e)f'(x)+f（x）ln2ln8ln9ln3ln3，所以f(k)f(3)26633e极大值．(e，+∞)–8n n 1n. kmax取q 33，当k=1，2，3，4，5时，ln kkln q，即k q k，经检验知q k 1k也成立．因此所求m的最大值不小于5．若m≥6，分别取k=3，6，得3≤q，且q≤6，从而q≥243，且q≤216，所以q不存在.因此所求m的最大值小于6.综上，所求m的最大值为5．【名师点睛】本题主要考查等差和等比数列的定义、通项公式、性质等基础知识，考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力．12．【2019年高考浙江卷】设等差数列{a}n 的前n项和为S，a 4，a S，数列{b}n343n满足：对每个n N ,S b,Sn n n 1b,Sn n 2bn成等比数列．（I）求数列{a},{b}n n的通项公式；（II）记ac n,n N2bn,证明：c c+12c 2n,n Nn.【答案】（I）a 2n 1，b n n 1nn；（II）证明见解析.【解析】（I）设数列{a}n的公差为d，由题意得a 2d 4,a 3d 3a 3d111，解得从而a 0,d 2．1a 2n 2,n Nn*．所以S n2n，n N*n，由S b,Sn n n 1b,Sn n 2bn成等比数列得S n 1bn2S bn nSn 2bn．解得bn 1dS2S Sn 1n n 2．所以b n2n,n N*n ．351515n9（II ）a2n 2 n 1 c n, n N 2b2n (n 1)n (n 1)n*． 我们用数学归纳法证明．（i ）当n =1时，c =0<2，不等式成立；（ii ）假设 n k k N * 时不等式成立，即nk 1 那么，当 时， cc12c2 k k．cccc 12k k 12 kk1 2 k(k 1)(k 2)k 12 k2 k 1 k2 k 2( k 1 k ) 2 k 1．即当n k 1时不等式也成立．根据（i ）和（ii ），不等式ccc2 n 对任意 n N12n*成立．【名师点睛】本题主要考查等差数列、等比数列、数列求和、数学归纳法等基础知识，同时考查运算 求解能力和综合应用能力.13 ．【四川省峨眉山市2019 届高三高考适应性考试数学试题】在等差数列{a }中， a ， a 是方程n39x 224 x 12 0的两根，则数列A ．66 C ． 66{a }n的前 11 项和等于 B ．132D ． 32【答案】D【解析】因为 a ， a 是方程 x 224 x 12 0 的两根，39所以a a24 39，又aa24 2a ，所以 a12 3966，S1111(a a ) 112a1 11 6 132 2 2，故选 D.【名师点睛】本题主要考查了等差数列的性质，等差中项，数列的求和公式，属于中档题.14．【四川省百校 2019 年高三模拟冲刺卷数学试题】定义在上的函数满足：当时，； 当时 ，. 记 函 数的 极 大 值 点 从 小 到 大 依 次 记 为并记相应的极大值为则的值为10n1A．C．【答案】A B．D．【解析】由题意当时，f(x)2x x2(x 1)21极大值点为1，极大值为1，当时，f(x)3f x 2.则极大值点形成首项为1公差为2的等差数列，极大值形成首项为1公比为3的等比数列，故设S= 3S=.,故，，，两式相减得-2S=1+2()-∴S=故选：A.，【名师点睛】本题考查数列与函数综合,错位相减求和,确定及的通项公式是关键,考查计算能力,是中档题.15．【福建省2019届高三毕业班质量检查测试数学试题】数列中，，且a a n n 1na an n 12(n 2)，则数列前2019项和为A．【答案】B 【解析】：∵B．C．（）D．∴an 2a2n 12a a nn﹣1n，整理得：，∴，又，∴可得：则数列故选：B．，．前2019项和为：．11，【名师点睛】本题主要考查了数列递推关系、“累加求和”方法、裂项求和，考查了推理能力、转化能力与计算能力，属于中档题．16．【内蒙古2019届高三高考一模试卷数学试题】《九章算术》第三章“衰分”介绍比例分配问题：“衰分”是按比例递减分配的意思,通常称递减的比例(百分比)为“衰分比”．如：甲、乙、丙、丁“哀”得100,60, 36,21.6个单位,递减的比例为40%,今共有粮m(m 0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和为164石,则“衰分比”与m的值分别为A．20%369B．80%36940%360C．【答案】A【解析】设“衰分比”为a,甲衰分得b石,D．60%365由题意得b (1a)280b (1a)b(1a)3164, b 80164m解得b 125,a 20%,m 369故选A．．【名师点睛】本题考查等比数列在生产生活中的实际应用,是基础题,解题时要认真审题,注意等比数列的性质的合理运用．17．【山东省德州市2019届高三第二次练习数学试题】设数列a的前n项和为S，已知a 1，a 2n n12且a 2S S 3，记b log a log a，则数列1n b 2的前10项和为______．n 2n n 1n22n 122n n【答案】200，【解析】∵a 1，a 2，且a 2S S 312n 2n n 1，∴a 23 3 23，∵a 2S S 3n 2n n 1，∴n 2时，a 2S S 3n 1n 1n，两式相减可得，an2an12S Sn n1Sn1Sn，（n 2）即n 2时，a a 2a a即a 2a n2n 1n n 1n 2n，∵a 2a31，12∴数列{a } n的奇数项和偶数项分别成等比数列，公比均为 2，∴a 2n2 2n 1 2n ，a2n 112n 1 2n 1，∴ blog alog an 1n 2n 1 ，n2 2n 12 2n则数列1nb 21n2n 12，则1nbnn2的前 10 项和为S3212725219217224122028 36200.故答案为 200.【名师点睛】本题考查数列的递推公式在数列的通项公式求解中的应用，考查等比数列的通项公式及 数列的求和方法的应用，属于中档题.18．【广东省深圳市高级中学 2019 届高三适应性考试（6 月)数学试题】在数列a中，n11a, a a,( n N *) 2019n (n 1)【答案】1，则 a 的值为______． 2019【解析】因为aan 1n1 n (n 1),( nN)所以a an 1n1 1 1 n (n 1) n n 1，1 a a 1 , 211 1 aa, 2 3...,a2019a20181 1 2018 2019, 各式相加，可得a a 1 2019 1 1 2019，1 1a 11n 1n23 220192019，13所以，a 12019，故答案为1.【名师点睛】本题主要考查利用递推关系求数列中的项，属于中档题.利用递推关系求数列中的项常见思路为：（1）项的序号较小时，逐步递推求出即可；（2）项的序数较大时，考虑证明数列是等差、等比数列，或者是周期数列；（3）将递推关系变形，利用累加法、累乘法以及构造新数列法求解.19．【2019北京市通州区三模数学试题】设an 是等比数列，且a a24a，a 2754，则an的通项公式为_______．【答案】a 3，n N .n【解析】设等比数列an的公比为q，因为所以a a a，a 27，2454aa a q25q2q327424，解得q 3，所以a27a41q327，因此，a 3n 1n，n N .故答案为a 3n 1n，n N .【名师点睛】本题主要考查等比数列基本量的计算，熟记等比数列的通项公式即可，属于常考题型.20．【重庆西南大学附属中学校2019届高三第十次月考数学试题】已知等差数列an 的前n项和为S，等n比数列bn 的前n项和为Tn．若a b 3，a b1142，S T 124 2．（I）求数列an 与bn的通项公式；（II）求数列a bn n的前n项和．【答案】（I）a 2n 1,b 3n n n；（II）n(n 2)33n 12.【解析】（I）由a b，a b1142，则S T (a a a a)(b b )a a 124 2 1 2 3 4 1 2 2 3，设等差数列an 的公差为d，则a2a 2a 3d 63d 12 n 1a13 1d 2.，所以所以a 32(n 1)2n 1.n14设等比数列b的公比为q，由题nb a 924，即b b q 3q 92 1，所以q 3.所以b 3nn；（II）a b (2n 1)3n ，n n所以a bn n 的前n项和为(a1a a)(b b b)2n12n(352n 1)(3323) (32n 1)n 3(13n)213n(n 2)3(3n 1)2.【名师点睛】本题主要考查等差数列与等比数列，熟记通项公式、前n项和公式即可，属于常考题型.21．【山东省烟台市2019届高三3月诊断性测试数学试题】已知等差数列{a}n 成等比数列．的公差是1，且a，a，a139（I）求数列{a }n的通项公式；（II）求数列{an}2a n的前n项和T．n【答案】（I）a nn；（II）T 2n 2n 2n.【解析】（I）因为{a }n 是公差为1的等差数列，且a，a，a成等比数列，139所以a23a a，即(a 2)1912a(a 8)11，解得a 11.所以a a (n 1)d nn1.111（II）T 1232221n ，21 211T122211(n 1)n22n 1，1111两式相减得T222211n1，1112 22 11n 1n1n 11n1.1n2n 1n123nn23n n123 nnn22所以Tn12所以T 2n 2n 2n.15【名师点睛】本题考查了等差数列与等比数列的通项公式、错位相减法，考查了推理能力与计算能力，属于常考题型．22．【安徽省1号卷A10联盟2019年高考最后一卷数学试题】已知等差数列a 1,a是的等比中项.24a 的通项公式；（I）求数列n an满足a 6a，且a 1633（II）设bn1a an n 1nN，数列b的前项和为T，求使T 1n n n成立的最大正整数的值【答案】（I）a 2n 1n.（II）8.【解析】（I）设等差数列an 的公差为d，Q a a 3d 663，即d 2，a 1a 3，a 1a 1，a a 6312141Q a 1是a 1，a的等比中项，324，a 12a 1 a324，即a+32=a 1a6111，解得a 31.数列a的通项公式为n a 2n 1 n.（II）由（I）得bn1a an n 1111 12n 12n 322n 12n 3.T b bb n1 2n 1 111111 235572n 12n 31 11n232n 332n3，由n132n 37，得n 9.使得T 1n成立的最大正整数n的值为8.【名师点睛】本题考查等差数列通项公式以及裂项相消法求和，考查基本分析求解能力，属中档题.23．【重庆一中2019届高三下学期5月月考数学试题】已知数列{a}n 满足：a 1n，an 121ann N ，n16数列{b } n中，bn1 a1n，且 b ， b ， b 成等比数列.124（I ）求证：数列{b } n是等差数列；（II ）若Sn是数列{b } n1 n nn.【答案】（I ）见解析；（II ） 2n n 1.【解析】（I ）bbn 1 n111 1a 1a1 a1 1a 1 n 1 n 1nn a 1 a 1annn，∴数列{b } n是公差为 1 的等差数列；（II ）由题意可得b 2 2b b 1 4，即b 112b 1b 1 3，所以b 1 ，所以 b1 1n，n (n 1) 1 2 1 1 ∴ S，∴ 22 S n (n 1) n n 1n，1 1 1 1 1 T2 12 12 2 3n n 11n 12n n 1.【名师点睛】本题主要考查等差数列性质的证明，考查等差数列的前 n 项和的求法，考查裂项相消法 求和，意在考查学生对这些知识的理解掌握水平和分析推理能力.17的前 项和，求数列 的前 项和 T S n 2 1 nn。

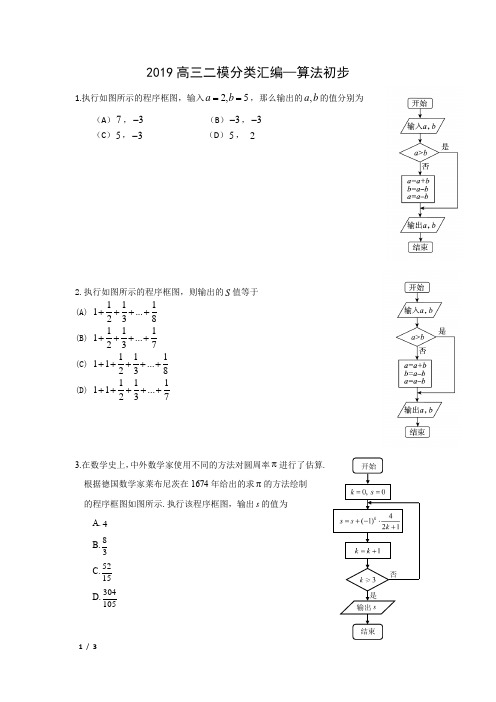
2019高三二模分类汇编—算法初步1.执行如图所示的程序框图，输入2,5a b ==，那么输出的,a b 的值分别为（A ）7，3- （B ）3-，3- （C ）5，3- （D ）5， 22.执行如图所示的程序框图，则输出的S 值等于(A) 1111...238++++ (B)1111...237++++(C)11111...238+++++(D)11111...237+++++3.在数学史上，中外数学家使用不同的方法对圆周率π进行了估算. 根据德国数学家莱布尼茨在1674年给出的求π的方法绘制 的程序框图如图所示.执行该程序框图，输出s 的值为 A.4 B.83 C.5215 D.304105开始结束输出 是否x < 1y =x 2-2x是否输出 y 结束输入x开始y =2x4．执行如图所示的程序框图，如果输入的[0,2]x ∈，那么输出的y 值不可能为 （A ）1- （B ）0 （C ）1（D ）25．中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”现给出该问题算法的程序框图，其中)(mod m n N ≡表示正整数N 除以正整数m 后的余数为n ，例如)3(mod 211≡表示11除以3后的余数是2.执行该程序框图，则输出的N 等于A ．7 B. 8 C. 9 D. 106.执行如图所示的程序框图，则输出的S 值为(A) 4(B) 5 (C) 8 (D) 9开始 S =0， n =1 a =7-2nn=n+1S =S +a a >0输出结束2019高三二模分类汇编—算法初步答案部分1.D2.D3.C4.D5.B6.D。

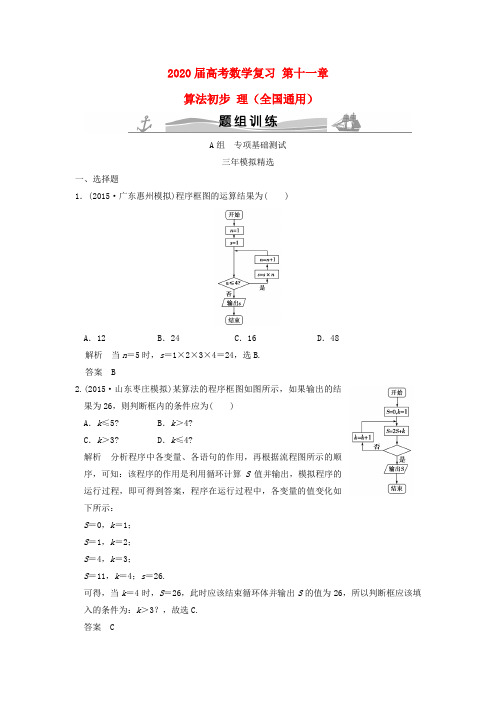
2020届高考数学复习第十一章算法初步理（全国通用）A组专项基础测试三年模拟精选一、选择题1．(2015·广东惠州模拟)程序框图的运算结果为( )A．12 B．24 C．16 D．48解析当n＝5时，s＝1×2×3×4＝24，选B.答案 B2.(2015·山东枣庄模拟)某算法的程序框图如图所示，如果输出的结果为26，则判断框内的条件应为( )A．k≤5? B．k＞4?C．k＞3? D．k≤4?解析分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算S值并输出，模拟程序的运行过程，即可得到答案，程序在运行过程中，各变量的值变化如下所示：S＝0，k＝1；S＝1，k＝2；S＝4，k＝3；S＝11，k＝4；s＝26.可得，当k＝4时，S＝26，此时应该结束循环体并输出S的值为26，所以判断框应该填入的条件为：k＞3？，故选C.答案 C3．(2014·大连模拟)如图是输出的值为1＋13＋15＋…＋199的一个程序框图，框内应填入的条件是( ) A ．i ≤99?B ．i <99?C ．i ≥99?D ．i >99?解析 S ＝0，i ＝1；S ＝1，i ＝3；S ＝1＋13，i ＝5；…；S ＝1＋13＋…＋197，i ＝99；S ＝1＋13＋…＋199，i ＝101，输出结果， 故填入“i ≤99？”，故选A. 答案 A第3题图 第4题图4．(2014·山西省四校联考)执行如图所示的程序框图后，输出的值为4，则P 的取值范围是( ) A.78<P ≤1516B ．P >1516C.78≤P <1516D.34<P ≤78解析 依题意得，当执行题中的程序框图后，输出的值为4时，数列⎩⎨⎧⎭⎬⎫12n 的前3项和开始不小于P .又数列⎩⎨⎧⎭⎬⎫12n 前2，3项和分别等于12＋14＝34，12＋14＋18＝78，因此P 的取值范围是34<P≤78，故选D. 答案 D5.(2014·安徽省名校联考)如图所示，该程序运行后输出 的结果为( ) A ．14 B ．16 C ．18D ．64解析 结合程序框图可知输出的S 值为8个2相加，即为16，故选B. 答案 B 二、填空题6．(2015·安徽马鞍山模拟)已知实数x ∈{1，2，3，4，5，6，7，8，9}，执行如图所示的程序框图，则输出的x 不小于121的概率为________．解析 经过第一次循环得到x ＝3x ＋1，n ＝2，经过第二循环得到x ＝3(3x ＋1)＋1，n ＝3， 经过第三次循环得到x ＝3[3(3x ＋1)＋1]＋1，n ＝4，此时输出x ，输出的值为27x ＋13，令27x ＋13≥121，得x ≥4，由古典概型得到输出的x 不小于121的概率为23.答案 23一年创新演练7．执行如图所示的程序框图，若输出的结果是8，则输入的数是________．解析 由a ≥b 得x 2≥x 3，解得x ≤1.所以当x ≤1时，输出a ＝x 2，当x >1时，输出b ＝x 3.所以当x ≤1时，由a ＝x 2＝8，解得x ＝－8＝－2 2.若x >1，由b ＝x 3＝8，得x ＝2，所以输入的数为2或－2 2. 答案 2或－2 28．执行如图所示的程序框图，若输入的a 值为2，则输出的P 值是________．解析 第一次循环，P ＝1＋1＝2，S ＝1＋12＝32；第二次循环，P ＝2＋1＝3，S ＝32＋13＝116；第三次循环，P ＝3＋1＝4，S ＝116＋14＝2512>2，因此输出的P 值为4.答案 4B 组 专项提升测试 三年模拟精选一、选择题9．(2015·河南省三市调研)某程序框图如图所示，则该程序运行后输出的S 的值为( )A ．1B.12C.14D.18解析 依题意得，运行程序后输出的是数列{a n }的第2 013项，其中数列{a n }满足：a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧2a n ，a n <118a n ，a n ≥1.注意到a 2＝18，a 3＝14，a 4＝12，a 5＝1，a 8＝18，…，该数列中的项以4为周期重复性地出现，且2 013＝4×503＋1，因此a 2 013＝a 1＝1，运行程序后输出的S 的值为1，故选A. 答案 A 二、填空题10．(2014·江西省盟校联考)如图是某算法的程序框图，则程序运行后输出的结果是________．解析 依题意得，题中的程序框图运行后输出的结果是数列{(－1)n＋n }的前n 项和大于9时的最小值．由于数列{(－1)n＋n }的前n 项和等于－[1－（－1）n]1－（－1）＋n （n ＋1）2＝（－1）n ＋n （n ＋1）－12，且（－1）3＋3（3＋1）－12＝5<9，（－1）4＋4（4＋1）－12＝10>9，因此程序运行后输出的结果是10.答案 1011．(2014·皖南八校三模)如图，运行该程序框图，则输出的结果为________．解析 由框图知，S ＝11×2＋12×3＋…＋110×11＝1－12＋12－13＋…＋110－111＝1－111＝1011.答案101112．(2014·潍坊二模)下列程序框图中，语句1将被执行的次数为________．解析 ∵循环次数＝循环终值－初值步长＋1，又∵循环的初值为1，退出循环时终值为100，步长为3，故循环次数为100－13＋1＝34.答案 34一年创新演练13．某市某机构调查小学生课业负担的情况，设平均每人每天做作业时间为X (单位：分钟)，按时间分下列四种情况统计：①0～30分钟；②30～60分钟；③60～90分钟；④90分钟以上．有1 000名小学生参加了此项调查，如图是此次调查中某一项的程序框图，其输出的结果是600，则平均每天做作业时间在0～60分钟内的学生的频率是________．解析 程序框图计算的是X >60的学生数，所以平均每天做作业时间在0～60分钟内的学生频率为4001 000＝0.4.答案0.414．如图是判断“美数”的流程图，在[30，40]内的所有整数中，“美数”的个数是________．解析依题意可知，题中的“美数”包括12的倍数与能被3整除但不能被6整除的数，由此不难得知，在[30，40]内的“美数”有3×11、3×12、3×13三个数．答案 3。

L 算法初步与复数L1 算法与程序框图14．L1[2020·江西卷] 如图1－3为某算法的程序框图，则程序运行后输出的结果是________．14．3 [解析] 考查算法框图、诱导公式、特殊角的三角函数值；解题的突破口是列出每一次循环后各变量的结果．当k ＝1时，此时sin π2＝1>sin0＝0成立，因此 a ＝1，T ＝0＋1＝1，k ＝1＋1＝2，k <6成立，再次循环；因sinπ＝0>sin π2＝1不成立，因此a ＝0，T＝1＋0＝1，k ＝2＋1＝3，此时k <6成立，再次循环；因sin 3π2＝－1> sinπ＝0不成立，因此a ＝0，T ＝1＋0＝1，k ＝3＋1＝4，此时k <6成立，再次循环；因sin2π＝0>sin 3π2＝－1成立，因此a ＝1，T ＝1＋1＝2，k ＝4＋1＝5，此时k <6成立，再次循环；因sin 5π2＝1> sin2π＝0成立，因此a ＝1，T ＝2＋1＝3，k ＝5＋1＝6，此时k <6不成立，退出循环，此时T ＝3.3．L1[2020·安徽卷] )的输出结果是( )A ．3B ．4C ．5D ．83．B [解析] 本题考查程序框图的应用，逻辑推理的能力． 用表格列出x ，y 每次的取值情况如下表：4．L1[2020·北京卷] 执行如图1－2所示的程序框图，输出的S 值为( )A．2 B．4 C．8 D．164．C [解析] 本题考查了循环结构的流程图，简单的整数指数幂计算等基础知识．根据循环，k＝0，S＝1；k＝1，S＝2；k＝2；S＝8，当k＝3，时，输出S＝8.12．L1[2020·福建卷] 阅读图1－2所示的程序框图，运行相应的程序，输出的s值等于________．12．－3 [解析] 第一次循环由于k＝1<4，所以s＝2－1＝1，k＝2；第二次循环k＝2<4，所以s＝2－2＝0，k＝3；第三次循环k＝3<4，所以s＝0－3＝－3，k＝4，结束循环，所以输出s＝－3.4．L1[2020·江苏卷] 图1－1是一个算法流程图，则输出的k的值是________．4．5 [解析] 本题为对循环结构的流程图的含义的考查．解题突破口为从循环终止条件入手，再一一代入即可．将k ＝1,2,3，…，分别代入可得k ＝5.13．L1[2020·广东卷] 执行如图1－2所示的程序框图，若输入n 的值为8，则输出s 的值为________．13．8 [解析] 考查程序框图的循环结构，突破口是计算每一次循环的情况，计算运算结果与执行情况，直到不满足条件为止，第一次循环：s ＝2，i ＝4，k ＝2；第二次循环：s ＝12×(2×4)＝4，i ＝6，k ＝3；第三次循环：s ＝13×(6×4)＝8，i ＝8，k ＝4，此时不满足条件：i <n ，结束循环，输出s ＝8. 14．L1[2020·湖南卷] 如果执行如图1－4所示的程序框图，输入x ＝－1，n ＝3，则输出的数S ＝________.图1－414．－4 [解析] 考查程序框图和数列的求和，考查考生的当型循环结构，关键是处理好循环次数，不要多加情况，或者少算次数．解决此类型试题，最好按循环依次写出结果．当i ＝2时S ＝－3，当i ＝1时S ＝5，当i ＝0时S ＝－4，当i ＝－1时，不满足条件，退出循环，输出结果S ＝－4.6．L1[2020·课标全国卷] 如果执行右边的程序框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则( )A ．A ＋B 为a 1，a 2，…，a N 的和 B.A ＋B 2为a 1，a 2，…，a N 的算术平均数C ．A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D ．A 和B 分别是a 1，a 2，…，a N 中最小的数和最大的数6．C [解析] 由程序框图可知，当x >A 时，A ＝x ；当x ≤A 且x <B 时，B ＝x ，所以A 是a 1，a 2，…，a N 中的最大数，B 是a 1，a 2，…，a N 中的最小数．故选C.9．L1[2020·辽宁卷] 执行如图S 值是( )图1－2A ．－1 B.23C.32 D ．49．A [解析] 本小题主要考查程序框图的应用．解题的突破口为分析i 与6的关系．当i ＝1时，S ＝22－4＝－1；当i ＝2时，S ＝22－－1＝23；当i ＝3时，S ＝22－23＝32；当i ＝4时，S ＝22－32＝4；当i ＝5时，S ＝22－4＝－1；当i ＝6时程序终止，故而输出的结果为－1.6．L1[2020·山东卷] 执行如图1－1所示的程序框图，如果输入a ＝4，那么输出的n 的值为( )A ．2B ．3C ．4D ．56．B [解析] 本题考查算法与程序框图，考查数据处理能力，容易题．当n ＝0时，P ＝1，Q ＝3，P <Q 成立，执行循环；当n ＝1时，P ＝5，Q ＝7，P <Q 成立，执行循环；当n ＝2时，P ＝21，Q ＝15，P <Q 不成立，但是n ＝2＋1＝3后，再输出．10．L1、K3[2020·陕西卷] 图1－3是用模拟方法估计圆周率π值的程序框图，P 表示估计结果，则图中空白框内应填入( )图1－3A ．P ＝N1000 B ．P ＝4N1000 C ．P ＝M 1000 D ．P ＝4M100010．D [解析] 本题主要考查循环结构的程序框图的应用，同时要兼顾考查学习概率的模拟方法中圆周率π的模拟，通过阅读题目和所给数据可知试验了1000次，M 代表落在圆内的点的个数，根据几何概型，π4＝M 1000，对应的圆周率π为P ＝4M1 000.3．L1[2020·天津卷] 阅读如图1－1所示的程序框图，运行相应的程序，当输入x 的值为－25时，输出x 的值为( )A ．－1B ．1C ．3D ．93．C [解析] 本题考查算法与程序框图，考查数据处理能力，容易题．经过第一次执行循环，x ＝|－25|－1＝4；经过第二次循环，x ＝|4|－1＝1；然后输出x ＝2×1＋1＝3.12．L1[2020·浙江卷] 若某程序框图如图1－4所示，则该程序运行后输出的值是________．12.1120 [解析] 本题主要考查算法的程序框图及其应用．当i ＝1时，T ＝11＝1，而i ＝1＋1＝2，不满足条件i >5；接下来，当i ＝2时，T ＝12，而i ＝2＋1＝3，不满足条件i >5；接下来，当i ＝3时，T ＝123＝16，而i ＝3＋1＝4，不满足条件i >5；接下来，当i ＝4时，T＝164＝124，而i ＝4＋1＝5，不满足条件i >5；接下来，当i ＝5时，T ＝1245＝1120，而i ＝5＋1＝6，满足条件i >5；此时输出T ＝1120，故应填1120.[点评] 对于程序框图问题，关键是正确识别与推理，通过逐步推理与分析加以正确判断．L2 基本算法语句 L3 算法案例 L4 复数的基本概念与运算11．L4[2020·重庆卷] 若(1＋i)(2＋i)＝a ＋b i ，其中a ，b ∈R ，i 为虚数单位，则a ＋b ＝________.11．4 [解析] 因为(1＋i)(2＋i)＝1＋3i ，则根据复数相等得a ＝1，b ＝3，所以a ＋b ＝4.2．L4[2020·浙江卷] 已知i 是虚数单位，则3＋i1－i＝( )A ．1－2iB ．2－iC ．2＋iD ．1＋2i2．D [解析] 本题主要考查复数的四则运算，检测学生对基础知识的掌握情况． 3＋i 1－i ＝3＋i 1＋i 1－i 1＋i ＝2＋4i2＝1＋2i ，故应选D.[点评] 复数的四则运算是每年高考的必考内容之一，以送分题为主．1．L4[2020·天津卷] i 是虚数单位，复数7－i3＋i＝( )A ．2＋iB ．2－iC ．－2＋iD ．－2－i1．B [解析] 本题考查复数的运算，考查运算求解能力，容易题． 7－i 3＋i ＝7－i 3－i 3＋i 3－i ＝7×3－1＋－3－7i32＋12＝2－i. 2．L4[2020·四川卷] 复数1－i22i＝( )A ．1B ．－1C ．iD ．－i2．B [解析] 由复数的代数运算，得(1－i)2＝－2i ，故原式＝－1.15．L4[2020·上海卷] 若1＋2i 是关于x 的实系数方程x 2＋bx ＋c ＝0的一个复数根，则( )A ．b ＝2，c ＝3B ．b ＝－2，c ＝3C ．b ＝－2，c ＝－1D ．b ＝2，c ＝－1 15．B [解析] 考查复数的概念和一元二次方程中根与系数的关系(即韦达定理)，可利用方程的两根是共轭复数解题．由韦达定理可知：－b ＝(1＋2i)＋(1－2i)＝2，∴b ＝－2，c ＝(1＋2i)(1－2i)＝1＋2＝3，∴c ＝3，所以选B.此题还可以直接把复数根1＋2i 代入方程中，利用复数相等求解．1．L4[2020·上海卷] 计算：3－i1＋i＝________(i 为虚数单位)．1．1－2i [解析] 考查复数的除法运算，是基础题，复数的除法运算实质就是分母实数化运算．原式＝3－i 1－i1－i2＝1－2i. 1．L4[2020·山东卷] 若复数z 满足z (2－i)＝11＋7i(i 为虚数单位)，则z 为( ) A ．3＋5i B ．3－5i C ．－3＋5i D ．－3－5i1．A [解析] 本题考查复数的概念及运算，考查运算能力，容易题．设z ＝a ＋b i ()a ，b ∈R ，由题意得()a ＋b i ()2－i ＝()2a ＋b ＋()2b －a i ＝11＋7i ，即⎩⎪⎨⎪⎧ 2a ＋b ＝11，2b －a ＝7，解之得⎩⎪⎨⎪⎧a ＝3，b ＝5. 2．L4[2020·辽宁卷] 复数2－i2＋i＝( )A.35－45iB.35＋45i C ．1－45i D ．1＋35i2．A [解析] 本小题主要考查复数的除法运算．解题的突破口为分子分母同乘以分母的共轭复数．因为2－i 2＋i ＝()2－i 2()2＋i ()2－i ＝3－4i 5＝35－45i ，所以答案为A.3．L4[2020·课标全国卷] 下面是关于复数z ＝2－1＋i的四个命题：p 1：|z |＝2，p 2：z 2＝2i ，p 3：z 的共轭复数为1＋i ，p 4：z 的虚部为－1，其中的真命题为( )A ．p 2，p 3B ．p 1，p 2C ．p 2，p 4D ．p 3，p 43．C [解析] 因为z ＝2－1＋i ＝2()－1－i ()－1＋i ()－1－i ＝－1－i ，所以z 的虚部是－1，z＝－1＋i ，||z ＝2，z 2＝()－1－i 2＝2i.故p 2，p 4是真命题， p 1，p 3是假命题，故选C.3．L4[2020·江苏卷] 设a ，b ∈R ，a ＋b i ＝11－7i1－2i(i 为虚数单位)，则a ＋b 的值为________．3．8 [解析] 本题考查复数的四则运算．解题突破口为将所给等式右边的分子、分母同时乘以分母的共轭复数即可．因为11－7i 1－2i ＝11－7i 1＋2i 5＝5＋3i ，所以a ＝5，b ＝3.12．L4[2020·湖南卷] 已知复数z ＝(3＋i)2(i 为虚数单位)，则|z |＝________.12．10 [解析] 复数z ＝(3＋i)2化简得，z ＝8＋6i ，所以|z |＝82＋62＝10.1．L4[2020·湖北卷] 方程x 2＋6x ＋13＝0的一个根是( ) A ．－3＋2i B ．3＋2i C ．－2＋3i D ．2＋3i1．A [解析] (解法一)x ＝－6±62－4×132＝－3±2i，故选A.(解法二)将A ，B ，C ，D 各项代入方程验证，发现只有A 项中的－3＋2i ，满足()－3＋2i 2＋6()－3＋2i ＋13＝9－12i －4－18＋12i ＋13＝0.故选A.1．L4[2020·广东卷] 设i 为虚数单位，则复数5－6ii＝( )A ．6＋5iB ．6－5iC ．－6＋5iD ．－6－5i1．D [解析] 因为5－6i i ＝5－6i i i·i ＝5i ＋6－1＝－6－5i ，所以选择D.1．L4[2020·福建卷] 若复数z 满足z i ＝1－i ，则z 等于( ) A ．－1－i B ．1－i C ．－1＋i D ．1＋i1．A [解析] 根据已知条件：z ＝1－i i ＝1－i ii·i＝－1－i.所以选择A.1．L4[2020·全国卷] 复数－1＋3i1＋i＝( )A ．2＋iB ．2－iC ．1＋2iD ．1－2i1．C [解析] 本小题主要考查复数的乘除法运算．解题的突破口为复数除法中的分母实数化．由－1＋3i 1＋i ＝－1＋3i 1－i 1＋i 1－i ＝2＋4i 2＝1＋2i ，故选C.1．L4[2020·安徽卷] 复数z 满足(z －i)(2－i)＝5，则z ＝( ) A ．－2－2i B ．－2＋2i C ．2－2i D ．2＋2i1．D [解析] 本题考查复数的简单运算．由()z －i ()2－i ＝5，得z －i ＝52－i ，所以z ＝i ＋5()2＋i ()2－i ()2＋i ＝2＋2i.3．A2、L4[2020·陕西卷] 设a ，b ∈R ，i 是虚数单位，则“ab ＝0”是“复数a ＋bi为纯虚数”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．B [解析] 本小题主要考查充要条件的概念以及复数的相关知识，解题的突破口为弄清什么是纯虚数，然后根据充要条件的定义去判断．a ＋b i ＝a －b i ，若a ＋bi 为纯虚数，a＝0且b ≠0，所以ab ＝0不一定有a ＋b i 为纯虚数，但a ＋bi 为纯虚数，一定有ab ＝0，故“ab＝0”是复数a ＋bi为纯虚数”的必要不充分条件，故选B.3．A2、L4[2020·北京卷] 设a ，b ∈R ，“a ＝0”是“复数a ＋b i 是纯虚数”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件3．B [解析] ∵若a ＝0，则复数a ＋b i 是实数(b ＝0)或纯虚数(b ≠0)．若复数a ＋b i 是纯虚数则a ＝0.综上，a ，b ∈R ，“a ＝0”是“复数a ＋b i 是纯虚数”的必要而不充分条件．L5 单元综合2020模拟题1．[2020·银川一中检测] 运行下面的程序，如果输入的n 是6，那么输出的p 是( ) INPUT “n＝”； n k ＝1 p ＝1WHILE k<＝n p ＝p*k k ＝k ＋1WEND PRINT p ENDA ．120B ．720C ．1440D ．50401. B [解析] 运行程序，k ＝1，p ＝1；k ＝2，p ＝2；k ＝3，p ＝6；k ＝4，p ＝24；k ＝5，p ＝120；k ＝6，p ＝720，输出720，选B.2．[2020·宁德质检] 运行如图K46－2所示的程序框图，输入下列四个函数，则可以输出的函数是( )A ．f (x )＝x 2B ．f (x )＝cos2xC ．f (x )＝e xD ．f (x )＝sinπx2．D [解析] 只有f (x )＝sinπx 满足f (x )＝0有解，且f (x )＝f (x ＋2)成立．3．[2020·温州检测] 如图K46－5给出的是计算12＋14＋16＋…＋12 012的值的一个程序框图，则判断框内应填入的条件是( )图K46－5A ．i ≤1 005?B ．i >1 005?C ．i ≤1 006?D ．i >1 006?3．C [解析] 因为执行程序框图，输出的是12＋14＋16＋…＋12 012，所以判断框内应填入的条件是i ≤1 006？.4. [2020·银川一中检测] 若i 为虚数单位，图K46－1中网格纸的小正方形的边长是1，复平面内点Z 表示复数z ，则复数z1－2i的共轭复数是( )图K46－1A ．－35i B.35I C ．－i D ．i 4．C [解析] 由题意z ＝2＋i ，所以z 1－2i ＝2＋i 1－2i ＝2＋i 1＋2i 1－2i1＋2i＝i ，则其共轭复数是－i ，选C. 5．[2020·延吉质检] 设z 1＝1＋i ，z 2＝1－i(i 是虚数单位)，则z 1z 2＋z 2z 1＝( )A ．－iB ．iC ．0D ．15．C [解析] 因为z 1＝1＋i ，z 2＝1－i ，所以z 1z 2＋z 2z 1＝1＋i 1－i ＋1－i 1＋i ＝i －i ＝0.。

2019年高考真题和模拟题分项汇编数学（理）：专题01 集合与常用逻辑用语（解析版）专题01 集合与常用逻辑用语1．【2019年高考全国Ⅰ卷理数】已知集合2|42{|60}{},M x x N x x x =-<<=--<，则MN =A ．}{43x x -<<B ．}42{x x -<<-C ．}{22x x -<<D ．}{23x x <<【答案】C【解析】由题意得2|42,{|60}{}|23}{M x x N x x x x x =-<<=--<=-<<， 则{|22}MN x x =-<<．故选C ．【名师点睛】注意区分交集与并集的不同，交集取公共部分，并集包括二者所有的部分． 2．【2019年高考全国Ⅱ卷理数】设集合A ={x |x 2–5x +6>0}，B ={x |x –1<0}，则A ∩B = A ．(–∞，1) B ．(–2，1)C ．(–3，–1)D ．(3，+∞)【答案】A【解析】由题意得，2{560|}{2|A x x x x x =-+><=或3}x >，{10}{1|}|B x x x x =-<=<，则{|1}(,1)A B x x =<=-∞．故选A ．【名师点睛】本题考点为集合的运算，为基础题目．3．【2019年高考全国Ⅲ卷理数】已知集合2{1,0,1,2},{|1}A B x x =-=≤，则A B =A ．{}1,0,1-B ．{}0,1C ．{}1,1-D ．{}0,1,2【答案】A【解析】∵21,x ≤∴11x -≤≤，∴{}11B x x =-≤≤，又{1,0,1,2}A =-，∴{}1,0,1A B =-.故选A ．【名师点睛】本题考查了集合交集的求法，是基础题.4．【2019年高考天津理数】设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ，则()AC B =A ．{}2B ．{}2,3C ．{}1,2,3-D ．{}1,2,3,4【答案】D 【解析】因为{1,2}A C =，所以(){1,2,3,4}A C B =.故选D .【名师点睛】集合的运算问题，一般要先研究集合中元素的构成，能化简的要先化简，同时注意数形结合，即借助数轴、坐标系、韦恩图等进行运算．5．【2019年高考浙江】已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则()U A B ð=A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-【答案】A【解析】∵{1,3}U A =-ð，∴(){1}U A B =-ð.故选A.【名师点睛】注意理解补集、交集的运算.6．【2019年高考浙江】若a >0，b >0，则“a +b ≤4”是 “ab ≤4”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【解析】当0, 0a >b >时，a b +≥，则当4a b +≤时，有4a b ≤+≤，解得4ab ≤，充分性成立；当=1, =4a b 时，满足4ab ≤，但此时=5>4a+b ，必要性不成立， 综上所述，“4a b +≤”是“4ab ≤”的充分不必要条件. 故选A.【名师点睛】易出现的错误：一是基本不等式掌握不熟练，导致判断失误；二是不能灵活地应用“赋值法”，通过取,a b 的特殊值，从假设情况下推出合理结果或矛盾结果.7．【2019年高考天津理数】设x ∈R ，则“250x x -<”是“|1|1x -<”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】由250x x -<可得05x <<，由|1|1x -<可得02x <<， 易知由05x <<推不出02x <<，由02x <<能推出05x <<，故05x <<是02x <<的必要而不充分条件，即“250x x -<”是“|1|1x -<”的必要而不充分条件. 故选B.【名师点睛】本题考查充分必要条件，解题的关键是由所给的不等式得到x 的取值范围. 8．【2019年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内有两条相交直线都与β平行是αβ∥的充分条件；由面面平行的性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内有两条相交直线都与β平行是αβ∥的必要条件. 故α∥β的充要条件是α内有两条相交直线与β平行. 故选B ．【名师点睛】面面平行的判定问题要紧扣面面平行的判定定理，最容易犯的错误为定理记不住，凭主观臆断.9．【2019年高考北京理数】设点A ，B ，C 不共线，则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】∵A ､B ､C 三点不共线，∴|AB +AC |>|BC |⇔|AB +AC |>|AC -AB |⇔|AB +AC |2>|AC -AB |2AB ⇔·AC >0AB ⇔与AC 的夹角为锐角，故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件. 故选C.【名师点睛】本题考查充要条件的概念与判断､平面向量的模､夹角与数量积，同时考查了转化与化归的数学思想.10．【2019年高考江苏】已知集合{1,0,1,6}A =-，{|0,}B x x x =>∈R ，则AB =▲ . 【答案】{1,6}【解析】由题意利用交集的定义求解交集即可.由题意知，{1,6}A B =.【名师点睛】本题主要考查交集的运算，属于基础题.11．【辽宁省沈阳市2019届高三教学质量监测（三）数学】已知集合{(,)|2,,}A x y x y x y =+≤∈N ，则A 中元素的个数为A ．1B ．5C ．6D ．无数个【答案】C【解析】由题得{(0,0),(0,1),(0,2),(1,0),(1,1),(2,0)}A =， 所以A 中元素的个数为6. 故选C.【名师点睛】本题主要考查集合的表示和化简，意在考查学生对这些知识的理解掌握水平和分析推理能力.12．【云南省玉溪市第一中学2019届高三上学期第二次调研考试数学】命题“2000,10x x x ∃∈++<R ”的否定为 A ．2000,10x x x ∃∈++≥RB ．2000,10x x x ∃∈++≤RC ．2000,10x x x ∀∈++≥R D ．2000,10x x x ∀∉++≥R【答案】C【解析】由题意得原命题的否定为2000,10x x x ∀∈++≥R .故选C.【名师点睛】本题考查含有一个量词的命题的否定，全称命题的否定是特称命题，特称命题的否定是全称命题.13．【黑龙江省大庆市第一中学2019届高三下学期第四次模拟（最后一卷)考试】已知集合{|1}A x x =<，{|31}x B x =<，则A ．{}1AB x x => B ．A B =RC ．{|0}AB x x =<D ．AB =∅【答案】C【解析】集合{|31}xB x =<，即{}0B x x =<，而{|1}A x x =<， 所以{}1A B x x =<，{}0A B x x =<.故选C.【名师点睛】本题考查集合的交集、并集运算，属于简单题.14．【北京市通州区2019届高三三模数学】已知集合{}0,1,2P =，{|2}Q x x =<，则PQ =A ．{}0B ．{0,1}C ．{}1,2D ．{0,2}【答案】B【解析】因为集合{0,1,2}P =，{|2}Q x x =<，所以{0,1}P Q =.故选B.【名师点睛】本题主要考查集合的交集运算，熟记概念即可，属于基础题型. 15．【北京市昌平区2019届高三5月综合练习（二模）数学】已知全集U =R ，集合2{|1}A x x =≤，则U A =ðA ．(,1)(1,)-∞-+∞B ．(,1][1,)-∞-+∞C ．(1,1)-D ．[1,1]-【答案】A【解析】因为2{|1}A x x =≤＝{|11}x x -≤≤， 所以U A =ð{|1x x <-或1}x >， 表示为区间形式即(,1)(1,)-∞-+∞.故选A.【名师点睛】本题主要考查集合的表示方法，补集的定义与运算等知识，意在考查学生的转化能力和计算求解能力.16．【福建省龙岩市（漳州市）2019届高三5月月考数学】已知集合}1|{≥=x x A ，{|230}B x x =->，则A B =A ．[0,)+∞B ．[1,)+∞C ．3,2⎛⎫+∞⎪⎝⎭D ．30,2⎡⎫⎪⎢⎣⎭【答案】B【解析】因为{|230}B x x =->=}23|{>x x ，}1|{≥=x x A ， 所以A B =[1,)+∞.故选B.【名师点睛】本题考查并集其运算，考查了不等式的解法，是基础题．17．【陕西省2019年高三第三次教学质量检测】设集合{|12,}A x x x =-≤≤∈N ，集合{2,3}B =，则B A 等于A ．{1,0,1,2,3}-B ．{0,1,2,3}C ．}3,2,1{D ．{2}【答案】B【解析】因为集合{|12,}{0,1,2}A x x x =-≤≤∈=N ，{2,3}B =， 所以0,1,3}2,{A B =.故选B ．【名师点睛】本题主要考查了集合的表示方法，以及集合的并集运算，其中正确求解集合A ，熟练应用集合并集的运算是解答的关键，着重考查了运算与求解能力，属于基础题.18．【湖北省安陆一中2019年5月高二摸底调考数学】已知集合{0,1,2}A =，{,2}B a =，若B A ⊆，则a =A ．0B ．0或1C ．2D ．0或1或2【答案】B【解析】由B A ⊆，可知{0,2}B =或{1,2}B =， 所以0a =或1. 故选B.【名师点睛】本小题主要考查子集的概念，考查集合中元素的互异性，属于基础题. 19．【天津市第一中学2019届高三下学期第五次月考数学】设x ∈R ，则“31x <”是“1122x -<”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B 【解析】由31x <可得1x <，由1122x -<可得01x <<， 据此可知“31x <”是“1122x -<”的必要而不充分条件. 故选B ．【名师点睛】本题主要考查不等式的解法，充分性与必要性的判定等知识，意在考查学生的转化能力和计算求解能力.20．【福建省龙岩市（漳州市)2019届高三5月月考数学】若1a >，则“y x a a >”是“log log a a x y >”的A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】由a >1，得y x a a >等价为x >y ；log log a a x y >等价为x >y >0，故“y x a a >”是“log log a a x y >”的必要不充分条件. 故选A.【名师点睛】本题主要考查充分条件和必要条件的判断，指数函数和对数函数的单调性，掌握充分条件和必要条件的定义是解决本题的关键．21．【河南省郑州市2019届高三第三次质量检测数学】“02m <<”是“方程2212x y m m+=-表示椭圆”的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件【答案】C【解析】方程2212x ym m +=-表示椭圆，即020022m m m m m>⎧⎪->⇒<<⎨⎪≠-⎩且1m ≠，所以“02m <<”是“方程2212x y m m+=-表示椭圆”的必要不充分条件.故选C.【名师点睛】本题考查了椭圆的概念，充分条件和必要条件的判断，容易遗漏椭圆中2m m ≠-，属于基础题.22．【四川省宜宾市2019届高三第三次诊断性考试数学】设是空间两条直线，则“不平行”是“是异面直线”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B 【解析】由是异面直线⇒不平行．反之，若直线不平行，也可能相交，不一定是异面直线．所以“不平行”是“是异面直线”的必要不充分条件．故选B ．【名师点睛】本题考查了异面直线的性质、充分必要条件的判定方法，属于基础题． 23．【北京市人大附中2019年高考信息卷（三）】设a ，b 为非零向量，则“a ∥b ”是“a 与b 方向相同”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】因为a ，b 为非零向量，所以a ∥b 时，a 与b 方向相同或相反， 因此“a ∥b ”是“a 与b 方向相同”的必要而不充分条件. 故选B ．【名师点睛】本题考查充要条件和必要条件的判断，属基础题.24．【江西省名校（临川一中、南昌二中)2019届高三5月联合考试数学】已知集合{}2230,A x x x =+-≤{}2B =<，则A B =A ．{}31x x -≤≤B ．{}01x x ≤≤ C ．{}31x x -≤< D ．{}10x x -≤≤【答案】B【解析】因为{}{}31,04A x x B x x =-≤≤=≤<， 所以A B ={}01x x ≤≤.故选B.【名师点睛】本题主要考查集合的化简和交集运算，意在考查学生对这些知识的理解掌握水平和分析推理能力.25．【广东省深圳市高级中学2019届高三适应性考试（6月）数学】已知集合{|A x y ==，2{|log 1}B x x =≤，则A B =A ．1{|}3x x ≤≤-B ．{|01}x x <≤C ．{|32}-≤≤x xD ．{|2}x x ≤【答案】B【解析】由二次根式有意义的条件，可得(1)(3)0x x -+≥， 解得31x -≤≤，所以{|A x y =={|31}x x =-≤≤.由对数函数的性质可得22log log 2x ≤， 解得02x <≤，所以2{|log 1}B x x =≤{|02}x x =<≤， 所以A B ={|01}x x <≤.故选B ．【名师点睛】研究集合问题，一定要抓住元素，看元素应满足的属性.研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质是求满足属于集合A 且属于集合B 的元素的集合.26．【山东省烟台市2019届高三5月适应性练习（二）数学】设集合{|A x y ==，{|2,x B y y ==3}x ≤，则集合()A B =R I ðA ．}3|{<x xB ．{|3}x x ≤C ．{|03}x x <<D ．{|03}x x <≤ 【答案】C【解析】因为{}{|3A x y x x ===≥，所以{}3A x x =<R ð，又{}{}|2,3|08xB y y x y y ==≤=<≤，所以(){}03A B x x =<<R ð.故选C ．【名师点睛】本题考查了集合的交集运算、补集运算，正确求出函数3-=x y 的定义域，函数2,3xy x =≤的值域是解题的关键.27．【辽宁省沈阳市2019届高三教学质量监测（三）】“3k =”是“直线:(2)l y k x =+与圆221x y +=相切”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【解析】因为直线:(2)l y k x =+与圆221x y +=相切，1,=则k =.所以“3k =”是“直线:(2)l y k x =+与圆221x y +=相切”的充分不必要条件. 故选A.【名师点睛】本题主要考查直线和圆的位置关系和充分不必要条件的判定，意在考查学生对这些知识的理解掌握水平和分析推理能力.28．【北京市朝阳区2019届高三第二次（5月）综合练习（二模)数学】已知等差数列{}n a 的首项为1a ，公差0d ≠，则“139,,a a a 成等比数列” 是“1a d =”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】C【解析】若139,,a a a 成等比数列，则2319a a a =，即2111(2)(8)a d a a d +=+，变形可得1a d =，则“139,,a a a 成等比数列”是“1a d =”的充分条件；若1a d =，则3123a a d d =+=，9189a a d d =+=，则有2319a a a =，则“139,,a a a 成等比数列”是“1a d =”的必要条件. 综合可得：“139,,a a a 成等比数列”是“1a d =”的充要条件. 故选C ．【名师点睛】本题考查等差数列的通项公式、等比数列的性质，充分必要条件的定义与判断，属于基础题．29．【江西省新八校2019届高三第二次联考数学】若“3x >”是“x m >”的必要不充分条件，则m 的取值范围是________． 【答案】(3,)+∞【解析】因为“3x >”是“x m >”的必要不充分条件， 所以(),m +∞是()3,+∞的真子集，所以3m >， 故答案为(3,)+∞.【名师点睛】本题考查根据必要不充分条件求参数的值，由题意得到(),m +∞是()3,+∞的真子集是解答的关键，属于基础题.30．【甘肃省酒泉市敦煌中学2019届高三一诊数学】设集合则=__________.【答案】【解析】求解绝对值不等式可得， 求解函数的值域可得，由交集的定义可知：.故答案为.【名师点睛】本题主要考查绝对值不等式的解法，函数的值域，交集的定义及其应用等知识，意在考查学生的转化能力和计算求解能力.31．【河北省衡水市2019届高三下学期第三次质量检测数学】设为两个不同平面，直线，则“”是“”的__________条件.【答案】充分不必要⊂，【解析】根据题意，α，β表示两个不同的平面，直线mα当α∥β时，根据面面平行的性质定理可知，α中任何一条直线都平行于另一个平面，得，所以α∥β；⊂时，α∥β或α与β相交，当且mα所以“”是“”的充分不必要条件．故答案为充分不必要．【名师点睛】本题主要考查了面面平行的性质定理，面面的位置关系，充分条件和必要条件定义的理解，属于基础题．32．【安徽省江淮十校2019届高三第三次联考数学】若命题“，”的否定是假命题，则实数的取值范围是__________.【答案】【解析】因为命题的否定是假命题，所以原命题为真命题，即不等式对恒成立，又在上为增函数，所以，即.故实数的取值范围是：.【名师点睛】本题考查命题否定的真假以及不等式恒成立问题，考查基本分析能力和转化求解能力，属中档题.2020年高考真题和模拟题分项汇编数学（理）：专题04 立体几何专题04 立体几何1．【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D【答案】D 【解析】解法一：,PA PB PC ABC ==△为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分，2R ==344π33R V R =∴=π==，故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=，又90CEF ∠=︒，12CE AE PA x ∴===， AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =，D \为AC 的中点，1cos 2AD EAC PA x∠==，2243142x x x x+-+∴=，22121222x x x ∴+=∴==，，，PA PB PC ∴===又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==2R ∴=，344338V R ∴=π=π⨯=，故选D.【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决． 2．【2019年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．3．【2019年高考全国Ⅲ卷理数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线 【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,,22MF BF BM ==∴=BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．4．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：cm 3）是A ．158B ．162C ．182D ．324【答案】B【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯= ⎪⎝⎭. 故选B.【名师点睛】本题首先根据三视图，还原得到几何体——棱柱，根据题目给定的数据，计算几何体的体积，常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算.5．【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β【答案】B【解析】如图，G 为AC 中点，连接VG ，V 在底面ABC 的投影为O ，则P 在底面的投影D 在线段AO 上，过D 作DE 垂直于AC 于E ，连接PE ，BD ，易得PE VG ∥，过P 作PF AC ∥交VG 于F ，连接BF ，过D 作DH AC ∥，交BG 于H ，则,,BPF PBD PED αβγ=∠=∠=∠，结合△PFB ，△BDH ，△PDB 均为直角三角形，可得cos cos PF EG DH BDPB PB PB PBαβ===<=，即αβ>； 在Rt △PED 中，tan tan PD PDED BDγβ=>=，即γβ>，综上所述，答案为B.【名师点睛】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.常规解法下易出现的错误有，不能正确作图得出各种角，未能想到利用“特殊位置法”，寻求简便解法.6．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D 打印技术制作模型.如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =, AA =，3D打印所用原料密度为0.9 g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得，214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形， ∵四棱锥O −EFGH 的高为3cm ， ∴3112312cm 3O EFGH V -=⨯⨯=． 又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=，所以该模型体积为3214412132cm O EFGH V V V -=-=-=，其质量为0.9132118.8g ⨯=．【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.7．【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．【答案】40【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体，则几何体的体积()3142424402V =-⨯+⨯⨯=. 【名师点睛】本题首先根据三视图，还原得到几何体，再根据题目给定的数据，计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．8．【2019年高考北京卷理数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【答案】如果l ⊥α，m ∥α，则l ⊥m .【解析】将所给论断，分别作为条件、结论，得到如下三个命题： （1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内； （3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α. 故答案为：如果l ⊥α，m ∥α，则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断，分别作为条件、结论加以分析即可.9．【2019年高考天津卷理数】的正方形，若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________． 【答案】π4【解析】由题意，的正方形，，借助勾股定理，2=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为1，圆柱的底面半径为12， 故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭. 【名师点睛】根据棱锥的结构特点，确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.10．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是 ▲ .【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=， 因为E 为1CC 的中点，所以112CE CC =， 由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高， 所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中，往往需要注意理清整体和局部的关系，灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.的正弦值． 【解析】（1）连结B 1C ，ME ． 因为M ，E 分别为BB 1，BC 的中点， 所以ME ∥B 1C ，且ME =12B 1C ． 又因为N 为A 1D 的中点，所以ND =12A 1D ． 由题设知A 1B 1=DC ，可得B 1C =A 1D ，故ME =ND ， 因此四边形MNDE 为平行四边形，MN ∥ED ． 又MN ⊄平面EDC 1，所以MN ∥平面C 1DE ． （2）由已知可得DE ⊥DA ．以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所示的空间直角坐标系D −xyz ，则(2,0,0)A ，A 1(2，0，4)，2)M ，(1,0,2)N ，1(0,0,4)A A =-，1(12)A M =--，1(1,0,2)A N =--，(0,MN =．设(,,)x y z =m 为平面A 1MA 的法向量，则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩m m ，所以2040x z z ⎧-+-=⎪⎨-=⎪⎩，．可取=m ．设(,,)p q r =n 为平面A 1MN 的法向量，则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩，．n n所以020p r ⎧=⎪⎨--=⎪⎩，．可取(2,0,1)=-n ．于是cos ,||⋅〈〉===‖m n m n m n ， 所以二面角1A MA N --【名师点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系，从而通过求解法向量夹角的余弦值来得到二面角的正弦值，属于常规题型.12．【2019年高考全国Ⅱ卷理数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值．【答案】（1）证明见解析；（2【解析】（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ， 故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知190BEB ∠=︒．由题设知Rt ABE △≌11Rt A B E △，所以45AEB ∠=︒， 故AE AB =，12AA AB =．以D 为坐标原点，DA 的方向为x 轴正方向，||DA 为单位长，建立如图所示的空间直角坐标系D –xyz ，则C （0，1，0），B （1，1，0），1C （0，1，2），E （1，0，1），(1,0,0)CB =，(1,1,1)CE =-，1(0,0,2)CC =．设平面EBC 的法向量为n =（x ，y ，x ），则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =（x ，y ，z ），则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =（1，1，0）． 于是1cos ,||||2⋅<>==-n m n m n m ．所以，二面角1B EC C --． 【名师点睛】本题考查了利用线面垂直的性质定理证明线线垂直以及线面垂直的判定，考查了利用空间向量求二角角的余弦值，以及同角的三角函数关系，考查了数学运算能力.13．【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°，将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2.（1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ； （2）求图2中的二面角B −CG −A 的大小.【答案】（1）见解析；（2）30.【解析】（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ⊥BE ，AB ⊥BC ，故AB ⊥平面BCGE ． 又因为AB ⊂平面ABC ，所以平面ABC ⊥平面BCGE ．（2）作EH ⊥BC ，垂足为H ．因为EH ⊂平面BCGE ，平面BCGE ⊥平面ABC ，所以EH ⊥平面ABC ．由已知，菱形BCGE 的边长为2，∠EBC =60°，可求得BH =1，EH以H 为坐标原点，HC 的方向为x 轴的正方向，建立如图所示的空间直角坐标系H –xyz ，则A （–1，1，0），C （1，0，0），G （2，0CG =（1，0），AC =（2，–1，0）．设平面ACGD 的法向量为n =（x ，y ，z ），则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩n n即0,20.x x y ⎧+=⎪⎨-=⎪⎩ 所以可取n =（3，6，又平面BCGE 的法向量可取为m =（0，1，0），所以cos ,||||⋅〈〉==n m n m n m ． 因此二面角B –CG –A 的大小为30°．【名师点睛】本题是很新颖的立体几何考题，首先是多面体折叠问题，考查考生在折叠过程中哪些量是不变的，再者折叠后的多面体不是直棱柱，最后通过建系的向量解法将求二面角转化为求二面角的平面角问题，突出考查考生的空间想象能力.14．【2019年高考北京卷理数】如图，在四棱锥P –ABCD 中，PA ⊥平面ABCD ，AD ⊥CD ，AD ∥BC ，PA =AD =CD =2，BC =3．E 为PD 的中点，点F 在PC 上，且13PF PC =． （1）求证：CD ⊥平面PAD ； （2）求二面角F –AE –P 的余弦值； （3）设点G 在PB 上，且23PG PB =．判断直线AG 是否在平面AEF 内，说明理由．【答案】（1）见解析；（2（3）见解析. 【解析】（1）因为PA ⊥平面ABCD ，所以PA ⊥CD ． 又因为AD ⊥CD ，所以CD ⊥平面PAD ． （2）过A 作AD 的垂线交BC 于点M ．因为PA ⊥平面ABCD ，所以PA ⊥AM ，PA ⊥AD ．如图建立空间直角坐标系A −xyz ，则A （0，0，0），B （2，-1，0），C （2，2，0），D （0，2，0），P （0，0，2）． 因为E 为PD 的中点，所以E （0，1，1）． 所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-=．所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭.设平面AEF 的法向量为n =（x ，y ，z ），则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩ 令z =1，则1,1y x =-=-．于是=(1,1,1)--n ．又因为平面PAD 的法向量为p =（1，0，0），所以cos ,||3⋅〈〉==-‖n p n p n p . 由题知，二面角F −AE −P（3）直线AG 在平面AEF 内． 因为点G 在PB 上，且2,(2,1,2)3PG PB PB ==--，所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭. 由（2）知，平面AEF 的法向量=(1,1,1)--n . 所以4220333AG ⋅=-++=n . 所以直线AG 在平面AEF 内.【名师点睛】（1）由题意利用线面垂直的判定定理即可证得题中的结论；（2）建立空间直角坐标系，结合两个半平面的法向量即可求得二面角F −AE −P 的余弦值；（3）首先求得点G 的坐标，然后结合平面AEF 的法向量和直线AG 的方向向量即可判断直线是否在平面内.15．【2019年高考天津卷理数】如图，AE ⊥平面ABCD ，,CF AE AD BC ∥∥，,1,2AD AB AB AD AE BC ⊥====．（1）求证：BF ∥平面ADE ；（2）求直线CE 与平面BDE 所成角的正弦值； （3）若二面角E BD F --的余弦值为13，求线段CF 的长．【答案】（1）见解析；（2）49；（3）87． 【解析】依题意，可以建立以A 为原点，分别以AB AD AE ，，的方向为x 轴，y 轴，z轴正方向的空间直角坐标系（如图），可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ，(0,0,2)E ．设(0)CF h h =>>，则()1,2,F h ．（1）依题意，(1,0,0)AB =是平面ADE 的法向量，又(0,2,)BF h =，可得0BF AB ⋅=，又因为直线BF ⊄平面ADE ，所以BF ∥平面ADE ．。

第十三章 算法初步、推理与证明、复数专题1 算法初步（理科）【三年高考】1.【2019高考新课标1卷】执行右面的程序框图,如果输入的011x y n ===，，,则输出x ,y 的值满足（A ）2y x = （B ）3y x = （C ）4y x = （D ）5y x =结束【答案】C【解析】当0,1,1x y n ===时,110,1112x y -=+=⨯=,不满足2236x y +≥；2112,0,21222n x y -==+==⨯=,不满足2236x y +≥；13133,,236222n x y -==+==⨯=,满足2236x y +≥；输出3,62x y ==,则输出的,x y 的值满足4y x =,故选C.2.【2019高考新课标3理数】执行下图的程序框图，如果输入的46a b ==，，那么输出的n =（ ）（A）3 （B）4 （C）5 （D）6【答案】B3．【2019年高考四川理数】秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为（A ）9 （B ）18 （C ）20 （D ）35【答案】B【解析】程序运行如下3,21,201224,10n x v i v i ==→==≥→=⨯+==≥ 4219,0092018,10,v i v i →=⨯+==≥→=⨯+==-<结束循环，输出18v =，故选B.4．【2019高考新课标2理数】中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图.执行该程序框图，若输入的2,2x n ==，依次输入的a 为2，2，5，则输出的s =（ ）（A ）7 （B ）12 （C ）17 （D ）34【答案】C【解析】由题意，当2,2,0,0x n k s ====，输入2a =，则0222,1s k =⋅+==，循环；输入2a =，则2226,2s k =⋅+==，循环；输入5a =，62517,32s k =⋅+==>，结束.故输出的17s =，选C.5．【2019年高考北京理数】执行如图所示的程序框图，若输入的a 值为1，则输出的k 值为（）A.1B.2C.3D.4【答案】B【解析】输入1=a ，则0=k ，1=b ；进入循环体，21-=a ，否，1=k ，2-=a ，否，2=k ，1=a ，此时1==b a ，输出k ，则2=k ，选B.6. 【2019高考新课标1，理9】执行右面的程序框图，如果输入的t =0.01，则输出的n =( )（A ）5 （B ）6 （C ）7 （D ）8【答案】C【解析】执行第1次，t =0.01,S =1,n =0,m =12=0.5,S =S -m =0.5,2m m ==0.25,n =1,S =0.5＞t =0.01,是，循环，执行第2次，S =S -m =0.25,2m m ==0.125,n=2,S=0.25＞t =0.01,是，循环， 执行第3次，S =S -m =0.125,2m m ==0.0625,n =3,S=0.125＞t =0.01,是，循环， 执行第4次，S =S -m =0.0625,2m m ==0.03125,n =4,S =0.0625＞t =0.01,是，循环， 执行第5次，S =S -m =0.03125,2m m ==0.015625,n =5,S =0.03125＞t =0.01,是，循环， 执行第6次，S =S -m =0.015625,2m m ==0.0078125,n =6,S=0.015625＞t =0.01,是，循环， 执行第7次，S =S -m =0.0078125,2m m ==0.00390625,n =7,S=0.0078125＞t=0.01,否，输出n =7，故选C.7.【2019高考北京，理3】执行如图所示的程序框图，输出的结果为（ ）A ．()22-，B ．()40-，C ．()44--，D ．()08-，开始x =1，y =1，k =0s =x -y ，t =x +yx =s ，y =tk =k +1k ≥3输出(x ，y )结束是否【答案】B8.【2019高考新课标2，理8】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入,a b 分别为14,18，则输出的a =()A ．0B ．2C ．4D ．14【答案】B【解析】程序在执行过程中，a ，b 的值依次为14a =，18b =；4b =；10a =；6a =；2a =；2b =，此时2a b ==程序结束，输出a 的值为2，故选B ．9.【2019江苏高考，4】根据如图所示的伪代码，可知输出的结果S 为________.【答案】7【解析】第一次循环：3,4S I ==;第二次循环：5,7S I ==;第三次循环：7,10S I ==;结束循环，输出7.S =10.【2019全国1高考理第7题】执行右面的程序框图，若输入的k b a ,,分别为1，2，3，则（第4题图）输出的M=（ ） A.320 B.27 C.516 D.815【答案】D【解析】程序在执行过程中，1,2,3a b k ===，1n =；1331,2,b ,2222M a n =+====； 28382,,b ,33323M a n =+====；3315815,,b ,428838M a n =+====，程序结束，输出158M =． 11.【2019江西高考理第7题】阅读如下程序框图，运行相对应的程序，则程序运行后输出的结果为（ ）A.7B.9C.10D.11【答案】B 【解析】第一次循环：11,lg ,3i S ==第二次循环：1313,lg lg lg ,355i S ==+= 第三次循环：1515,lg lg lg ,577i S ==+=第四次循环：1717,lg lg lg ,799i S ==+= 第五次循环：1919,lg lg lg 1,91111i S ==+=<-结束循环，输出9.i =选B. 12.【2019高考湖北卷理第13题】设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为()I a ，按从大到小排成的三位数记为()D a （例如815a =，则()158I a =，()851D a =）.阅读如图所示的程序框图，运行相对应的程序，任意输入一个a ，输出的结果b = .【答案】495【三年高考命题回顾】纵观前三年各地高考试题, 主要考查算法概念和程序框图，理解算法的基本结构，基本算法语句高考很少涉及．命题主要集中在算法的三种基本逻辑结构的框图表示，程序框图与其它知识结合是新的热点．【2019年高考复习建议与高考命题预测】由前三年的高考命题形式能够看出, 算法初步主要掌握算法概念和程序框图，理解算法的基本结构、基本算法语句，理解古代算法案例，体会蕴含的算法思想，增强有条理的思考与表达水平，提升逻辑思维水平．而高考命题主要集中在算法的三种基本逻辑结构的框图表示，程序框图与其它知识结合是新的热点．题目的位置也靠前，属于中低档题，估计2019年高考难度在中低档，基本出题方式不变，也可能变换一种考法，比如告诉输出结果，考查判断语句等是命题演变的趋势.算法不但是数学及其应用的重要组成部分，也是计算机科学的重要基础.算法初步虽然是新课标增加的内容，但与前面的知识有着密切的联系，并且与实际问题的联系也非常密切.所以，在高考中算法初步知识将与函数、数列、三角、概率、实际问题等知识点实行整合，是高考试题命制的新“靓”点.这样试题就遵循了“在知识网络交汇处设计试题”的命制原则，既符合高考命题“水平立意”的宗旨，又突出了数学的学科特点.这样做，能够从学科的整体高度和思维价值的高度考虑问题，能够揭示数学各知识之间得到的内在联系，能够使考查达到必要的深度.考查形式与特点是：（1）选择题、填空题主要考查算法的含义、流程图、基本算法语句等内容，一般在每份试卷中有1题，多为中档题出现. (2)在解答题中可通过让学生读程序框图去解决其它问题，此类试题往往是与数列题结合在一起，具有一定的综合性，能够考查学生的识图水平及对数列知识的掌握情况.复习建议：一般地讲，算法是人们解决问题的固定步骤和方法．在本模块中，我们应重点掌握的是在数值计算方面的算法．高考新课程标准数学考试大纲对《算法初步》的要求是：（1）算法的含义、流程图：①了解算法的含义，了解算法的思想；②理解流程图的三种基本逻辑结构：顺序结构、选择结构、循环结构．（2）基本算法语句：理解几种基本算法语句——输入语句、输出语句、赋值语句、选择语句、循环语句的含义．注意的是，考纲对算法的含义和算法的思想的要求是“了解”，而对流程图和基本算法语句的要求是“理解”．由此可见，复习中应把重点放在流程图和基本算法语句上，要对这两方面的内容重点掌握、多加练习．表达算法的方法有自然语言、流程图和基本算法语句三种．自然语言描述算法仅仅学习算法的一个过渡，流程图和基本算法语句才是学习的重点，同时也是难点，尤其是选择结构和循环结构，在复习中是重中之重．【2019年高考考点定位】高考对算法的考查有两种主要形式：一是直接考查程序框图；二是程序语言使用.从涉及的知识上讲，算法初步知识与函数、数列、三角、概率、实际问题等知识点实行整合，小题目综合化是这部分内容的一种趋势.【考点1】算法与程序框图【备考知识梳理】（1）算法的定义：广义的算法是指完成某项工作的方法和步骤，那么我们能够说洗衣机的使用说明书是操作洗衣机的算法，菜谱是做菜的算法等等.在数学中，现代意义的算法是指能够用计算机来解决的某一类问题的程序和步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成（2）描述算法能够用不同的方式.例如：能够用自然语言和数学语言加以叙述，也能够借助形式语言（算法语言）给出精锐的说明，也能够用程序框图直观的显示算法全貌.①自然语言就是人们日常使用的语言，能够是人之间来交流的语言、术语等，通过度步的方式来表达出来的解决问题的过程.其优点为：好理解，当算法的执行都是先后顺序时比较容易理解；缺点是：表达冗长，且不易表达清楚步骤间的重复操作、分情况处理现象、先后顺序等问题.②程序框图：程序框图是用规定的图形符号来表达算法的具体过程.优点是：简捷形象、步骤的执行方向直观明了.③程序语言：程序语言是将自然语言和框图所表达的解决问题的步骤用特定的计算机所识别的低级和高级语言编写而成.特点：能在计算机上执行，但格式要求严格（3）算法的特征：①确定性：算法的每一步都理应做到准确无误、“不重不漏”.“不重”是指不是可有可无的、甚至无用的步骤，“不漏”是指缺少哪一步都无法完成任务.②逻辑性：算法从开始的“第一步”直到“最后一步”之间做到环环相扣.分工明确，“前一步”是“后一步”的前提，“后一步”是“前一步”的继续.③有穷性：算法要有明确的开始和结束，当到达终止步骤时所要解决的问题必须有明确的结果，也就是说必须在有限步内完成任务，不能无限制的持续实行. 2．程序框图（1）程序框图的概念：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形；（2）构成程序框的图形符号及其作用（3）程序框图的构成一个程序框图包括以下几部分：实现不同算法功能的相对应的程序框；带箭头的流程线；程序框内必要的说明文字3．几种重要的结构（1）顺序结构顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序实行的.它是由若干个依次执行的步骤组成的，它是任何一个算法都离不开的一种基本算法结构.见示意图和实例：顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来，按顺序执行算法步骤.如在示意图中，A框和B框是依次执行的，只有在执行完A框指定的操作后，才能接着执行B框所指定的操作.（2）条件结构如下面图示中虚线框内是一个条件结构，此结构中含有一个判断框，算法执行到此判断给定的条件P是否成立，选择不同的执行框（A框、B框）.无论P条件是否成立，只能执行A框或B框之一，不可能既执行A框又执行B框，也不可能A框、B框都不执行.A框或B框中能够有一个是空的，即不执行任何操作见示意图（3）循环结构在一些算法中要求重复执行同一操作的结构称为循环结构.即从算法某处开始，按照一定条件重复执行某一处理过程.重复执行的处理步骤称为循环体.循环结构有两种形式：当型循环结构和直到型循环结构.①当型循环结构，如左下图所示，它的功能是当给定的条件P成立时，执行A框，A框执行完毕后，返回来再判断条件P是否成立，如果仍然成立，返回来再执行A框，如此反复执行A 框，直到某一次返回来判断条件P不成立时为止，此时不再执行A框，离开循环结构.继续执行下面的框图.②直到型循环结构，如右下图所示，它的功能是先执行重复执行的A框，然后判断给定的条件P是否成立，如果P仍然不成立，则返回来继续执行A框，再判断条件P是否成立.以次重复操作，直到某一次给定的判断条件P时成立为止，此时不再返回来执行A框，离开循环结构.继续执行下面的框图见示意图【规律方法技巧】1. 识别程序框图运行和完善程序框图的步骤识别运行程序框图和完善程序框图是高考的热点．解答这个类问题，第一，要明确程序框图的顺序结构、条件结构和循环结构；第二，要识别运行程序框图，理解框图所解决的实际问题；第三，按照题目的要求完成解答．对程序框图的考查常与数列和函数等知识相结合，进一步强化框图问题的实际背景．2.解决程序框图问题要注意几个常用变量：i i=+.(1)计数变量：用来记录某个事件发生的次数，如1=+.(2)累加变量：用来计算数据之和，如S S i=⨯.(3)累乘变量：用来计算数据之积，如p p i3. 程序框图问题的解法(1)解答程序框图的相关问题，首先要认清程序框图中每个“框”的含义，然后按程序框图运行的箭头一步一步向前“走”，搞清每走一步产生的结论．(2)要特别注意在哪一步结束循环，解答循环结构的程序框图，最好的方法是执行完整每一次循环，防止执行程序不彻底，造成错误．4.判断条件的注意事项解决此类问题应该注意以下三个方面：一是搞清判断框内的条件由计数变量还是累加变量来表示；二是要注意判断框内的不等式是否带有等号，这直接决定循环次数的多少；三是要准确利用程序框图的赋值语句与两个变量之间的关系，把握程序框图的整体功能，这样能够直接求解结果，减少运算的次数．5.画程序框图的规则如下：（1）一个完整的程序框图必须有起止框，用来表示程序的开始和结束.（2）使用标准的图形符号表示操作，带箭头的流程线表示算法步骤的先后顺序，框图一般按从上到下、从左到右的方向画（3）算法中间要处理数据或计算，可分别写在不同的处理框中.（4）如果一个流程因为纸面等原因需要分开画.要在断开处画上连结点，并标出连结的号码.如图一.实际上它们是同一点，仅仅化不才分开画.用连结点可避免流程线的交叉或过长，使流程图清晰.（5）注释框不是流程图必需的部分，仅仅为了提示用户一部分框图的作用以及对某些框图的操作结果实行说明.它协助阅读流程图的用户更好的理解流程图的来龙去脉.（6）在图形符号内用于描述的语言要非常简练清楚【考点针对训练】1. 【2019湖北华师一附中高三检测】若如下框图所给的程序运行结果为S =41，则图中的判断框①中应填入的是( )A ．6?i >B ．6?i ≤C ．5?i >D ．5?i <【答案】C2.【2019年江西九江高三三模】设22,21,20,19,1854321=====x x x x x ，将这五个数据依次输入下面程序框图实行计算，则输出的S 值及其统计意义分别是（ ）A ．2=S ，即5个数据的方差为2B ．2=S ，即5个数据的标准差为2C ．10=S ，即5个数据的方差为10D ．10=S ，即5个数据的标准差为10【答案】A 【解析】∵2])2022()2021()2020()2019()2018[(5122222=-+-+-+-+-=S ，∴选A.【考点2】算法与程序框图【备考知识梳理】1．输入语句输入语句的格式：INPUT “提示内容”； 变量例如：INPUT “x =”； x 功能：实现算法的输入变量信息（数值或字符）的功能.要求：（1）输入语句要求输入的值是具体的常量；（2）提示内容提示用户输入的是什么信息，必须加双引号，提示内容 “原原本本”的在计算机屏幕上显示，提示内容与变量之间要用分号隔开；（3）一个输入语句能够给多个变量赋值，中间用“，”分隔；输入语句还能够是“提示内容1”；变量1，“提示内容2”；变量2，“提示内容3”；变量3，……”的形式.例如：INPUT“a =，b =，c=，”；a ，b ，c.2．输出语句输出语句的一般格式：PRINT“提示内容”；表达式例如：PRINT“S=”；S功能：实现算法输出信息（表达式）要求：（1）表达式是指算法和程序要求输出的信息；（2）提示内容提示用户要输出的是什么信息，提示内容必须加双引号，提示内容要用分号和表达式分开.（3）如同输入语句一样，输出语句能够一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔；输出语句还能够是“提示内容1”；表达式1，“提示内容2”；表达式2，“提示内容3”；表达式3，……”的形式；例如：PRINT “a ,b ,c ：”；a ,b ,c.3．赋值语句赋值语句的一般格式：变量=表达式赋值语句中的“＝”称作赋值号作用：赋值语句的作用是将表达式所代表的值赋给变量；要求：（1）赋值语句左边只能是变量名字，而不是表达式，右边表达式能够是一个常量、变量或含变量的运算式.如：2=x 是错误的；（2）赋值号的左右两边不能对换.赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量.如“A =B ”“B =A ”的含义运行结果是不同的，如x =5是对的，5=x 是错的，A +B =C 是错的，C=A +B 是对的.（3）不能利用赋值语句实行代数式的演算.（如化简、因式分解、解方程等），如)1)(1(12+-=-=x x x y这是实现不了的.在赋值号右边表达式中每一个变量的值必须事先赋给确定的值.在一个赋值语句中只能给一个变量赋值.不能出现两个或以上的“=”.但对于同一个变量能够多次赋值.4．条件语句（1）“IF —THEN —ELSE ”语句格式：IF 条件 THEN语句1ELSE语句2END IF说明：在“IF—THEN —ELSE”语句中，“条件”表示判断的条件，“语句1”表示满足条件时执行的操作内容；“语句2”表示不满足条件时执行的操作内容；END IF 表示条件语句的结束.计算机在执行“IF—THEN—ELSE”语句时，首先对IF后的条件实行判断，如果符合条件，则执行THEN后面的“语句1”；若不符合条件，则执行ELSE后面的“语句2”.（2）“IF—THEN”语句格式：IF 条件THEN语句END IF说明：“条件”表示判断的条件；“语句”表示满足条件时执行的操作内容，条件不满足时，直接结束判断过程；END IF表示条件语句的结束.计算机在执行“IF—THEN”语句时，首先对IF后的条件实行判断，如果符合条件就执行THEN后边的语句，若不符合条件则直接结束该条件语句，转而执行其它后面的语句5．循环语句（1）当型循环语句当型（WHILE型）语句的一般格式为：WHILE 条件循环体WEND说明：计算机执行此程序时，遇到WHILE语句，先判断条件是否成立，如果成立，则执行WHILE 和WEND之间的循环体，然后返回到WHILE语句再判断上述条件是否成立，如果成立，再执行循环体，这个过程反复执行，直到一次返回到WHILE语句判断上述条件不成立为止，这时不再执行循环体，而是跳到WEND语句后，执行WEND后面的语句.所以当型循环又称“前测试型”循环，也就是我们经常讲的“先测试后执行”、“先判断后循环”.（2）直到型循环语句直到型（UNTIL型）语句的一般格式为：DO循环体LOOP UNTIL 条件说明：计算机执行UNTIL语句时，先执行DO和LOOP UNTIL之间的循环体，然后判断“LOOP UNTIL”后面的条件是否成立，如果条件成立，返回DO语句处重新执行循环体.这个过程反复执行，直到一次判断“LOOP UNTIL”后面的条件不成立为止，这时不再返回执行循环体，而是跳出循环体执行“LOOP UNTIL 条件”下面的语句.所以直到型循环又称“后测试型”循环，也就是我们经常讲的“先执行后测试”、“先循环后判断”.【规律方法技巧】1.涉及具体问题的算法时，要根据题目实行选择，以简单、程序短、易于在计算机上执行为原则.注意条件语句的两种基本形式及各自的应用范围以及对应的程序框图.条件语句与算法中的条件结构相对应，语句形式较为复杂，要会借助框图写出程序.利用循环语句写算法时，要分清步长、变量初值、终值，必须分清循环次数是否确定，若确定，两种语句均可使用，当循环次数不确定时用while 语句.2. 条件语句的主要功能是来实现算法中的条件结构.因为人们对计算机运算的要求不但仅是一些简单的代数运算，而是经常需要计算机按照条件实行分析、比较、判断，并且按照判断后的不同情况实行不同的操作和处理.如果是要解决像“判断一个数的正负”、“比较数之间的大小”，“对一组数实行排序”、“求分段函数的函数值”等很多问题，计算机就需要用到条件语句.条件结构的差异，造成程序执行的不同.当代入x 的数值时，“程序一”先判断外层的条件，依次执行不同的分支，才有可能判断内层的条件；而“程序二”中执行了对“条件1”的判断，同时也对“条件2”实行判断，是按程序中条件语句的先后依次判断所有的条件，满足哪个条件就执行哪个语句.3. 赋值语句在程序运行时给变量赋值；“=”的右侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；有计算功能；将一个变量的值赋给另一个变量时，前一个变量的值保持不变；可先后给一个变量赋多个不同的值，但变量的取值只与最后一次赋值相关. 关于赋值语句，有以下几点需要注意：①赋值号左边只能是变量名字，而不是表达式，例如3m =是错误的．②赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如y x =，表示用x 的值替代变量y 的原先的取值，不能改写为x y =.因为后者表示用y 的值替代变量x 的值．③在一个赋值语句中只能给一个变量赋值，不能出现两个或多个“＝”．4. 学习了循环语句的两种格式，我们来挖掘一下应用循环语句编写程序的“条件三要素”. 第一、循环语句中的变量一般需要实行一定的初始化操作.第二、循环语句在循环的过程中需要有“结束”的机会.程序中最忌“死循环”.所谓的“死循环”就是指该循环条件永远成立，没有跳出循环体的机会. 第三、在循环中要改变循环条件的成立因素程序每执行一次循环体，循环条件中涉及到的变量就会发生改变，正在步步逼近满足跳出循环体的条件.【考点针对训练】1. 【2019年江西师大附中高三模考】如右图，当输入5x =-，15y =时，图中程序运行后输出的结果为（ ）A ．3； 33B ．33；3 C.-17；7 D ．7；-17【答案】A【解析】因为0<x ,所以执行183=+=y x ，即此时18=x ，15=y ，输出为y x y x +-,，而33,3=+=-y x y x ，所以输出结果为33,3，本题准确选项为A.2. 【2019届陕西省高三高考全真模拟四】如图所示,当输入,a b 分别为2,3时,最后输出的M 的值是 .【答案】3【解析】由算法的伪代码程序语言可知输出的是两数2,3a b ==中最大的数,故应输出3，故应选C.【应试技巧点拨】1．识别程序框图运行和完善程序框图的步骤识别运行程序框图和完善程序框图是高考的热点．解答这个类问题，第一，要明确程序框图的顺序结构、条件结构和循环结构；第二，要识别运行程序框图，理解框图所解决的实际问题；第三，按照题目的要求完成解答．对程序框图的考查常与数列和函数等知识相结合，进一步强化框图问题的实际背景．2.解决程序框图问题要注意几个常用变量：i i=+.(1)计数变量：用来记录某个事件发生的次数，如1=+.(2)累加变量：用来计算数据之和，如S S i=⨯.(3)累乘变量：用来计算数据之积，如p p i3. 程序框图问题的解法(1)解答程序框图的相关问题，首先要认清程序框图中每个“框”的含义，然后按程序框图运行的箭头一步一步向前“走”，搞清每走一步产生的结论．(2)要特别注意在哪一步结束循环，解答循环结构的程序框图，最好的方法是执行完整每一次循环，防止执行程序不彻底，造成错误．4.判断条件的注意事项解决此类问题应该注意以下三个方面：一是搞清判断框内的条件由计数变量还是累加变量来表示；二是要注意判断框内的不等式是否带有等号，这直接决定循环次数的多少；三是要准确利用程序框图的赋值语句与两个变量之间的关系，把握程序框图的整体功能，这样能够直接求解结果，减少运算的次数．5.画程序框图的规则如下：（1）一个完整的程序框图必须有起止框，用来表示程序的开始和结束.（2）使用标准的图形符号表示操作，带箭头的流程线表示算法步骤的先后顺序，框图一般按从上到下、从左到右的方向画（3）算法中间要处理数据或计算，可分别写在不同的处理框中.（4）如果一个流程因为纸面等原因需要分开画.要在断开处画上连结点，并标出连结的号码.如图一.实际上它们是同一点，仅仅化不才分开画.用连结点可避免流程线的交叉或过长，使流程图清晰.（5）注释框不是流程图必需的部分，仅仅为了提示用户一部分框图的作用以及对某些框图的操作结果实行说明.它协助阅读流程图的用户更好的理解流程图的来龙去脉.（6）在图形符号内用于描述的语言要非常简练清楚6.解决循环结构框图问题，首先要找出控制循环的变量其初值、步长、终值(或控制循环的条件)，然后看循环体，循环次数比较少时，可依次列出即可获解，循环次数较多时可先循环几。

新《算法与框图》专题解析一、选择题1．执行如图所示的程序框图，输出的结果为（ ）A ．919B ．1021C ．1819D ．2021【答案】B 【解析】 【分析】根据程序框图得出2221114114214101S =+++⨯-⨯-⨯-L ，利用裂项相消法可求得输出的S 的值. 【详解】()()21111141212122121i i i i i ⎛⎫==- ⎪--+-+⎝⎭Q， 由程序框图可知，输出的S 的值为2221114114214101S =+++⨯-⨯-⨯-L 1111111012335192121⎛⎫=-+-++-= ⎪⎝⎭L . 故选：B. 【点睛】本题考查利用程序框图计算输出结果，同时也考查了裂项求和法的应用，考查计算能力，属于中等题.2．如图所示的程序框图是求3333---的值的程序，则判断框中应填入（ ）A ．1i ≥B ．5i ≤C ．5i >D ．7i ≤【答案】B 【解析】 【分析】根据框图，模拟程序的运算即可求解. 【详解】 由程序框图得，3S =，1i =，满足条件得33S =-，3i =，满足条件得333S =--， 5i =，满足条件3333S =---， 7i =，否，输出S 的值，结束程序， 因此判断框应该是5i ≤， 故选：B ． 【点睛】本题主要考查了算法的程序框图，基本逻辑结构中的循环结构，属中档题.3．执行如图所示的程序框图，若输出的S 的值为0，则中可填入( )A ．2m m =+B ．1=+m mC ．1m m =-D ．2m m =-【答案】A 【解析】 【分析】根据程序运行，将每一个选项代入试运行，算出其输出结果，从而选出答案. 【详解】对选项A ，2,4S m ==，则()2424S =⨯-=;4,6S m ==,则()4648S =⨯-=8,8S m ==,则()8880S =⨯-=,所以输出结果0S =,所以正确.对选项B ，2,4S m ==，则()2424S =⨯-=;4,5S m ==,则()4544S =⨯-= 4,6S m ==,则()4648S =⨯-=8,7S m ==,则()87880S =⨯-=-<，输出结果8S =-,所以不正确.对选项C ，2,4S m ==，则()2424S =⨯-=;4,3S m ==,则()43440S =⨯-=-<，输出结果4S =-,所以不正确.对选项D ，2,4S m ==，则()2424S =⨯-=;4,2S m ==,则()42480S =⨯-=-<,所以输出结果8S =-,所以不正确.故选：A 【点睛】本题考查程序框图中循环，考查补全程序结构，属于中档题.4．若执行下面的程序框图，输出的值为3，则判断框中应填入的条件是（ ）A ．7?k <B ．6?k <C ．9?k <D ．8?k <【答案】D 【解析】 【分析】根据程序框图，写出运行结果，根据程序输出的结果是S=3，可得判断框内应填入的条件． 【详解】根据程序框图，运行结果如下： S k 第一次循环 log 23 3 第二次循环 log 23•log 34 4 第三次循环 log 23•log 34•log 45 5 第四次循环 log 23•log 34•log 45•log 56 6 第五次循环 log 23•log 34•log 45•log 56•log 67 7第六次循环 log 23•log 34•log 45•log 56•log 67•log 78=log 28=3 8故如果输出S=3，那么只能进行六次循环，故判断框内应填入的条件是k ＜8． 故答案为：D ． 【点睛】本题考查程序框图，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律是解题关键.5．某程序框图如图所示，若输出S ＝3，则判断框中M 为（ ）A ．k ＜14？B ．k≤14？C ．k≤15？D ．k ＞15？【答案】B 【解析】 【分析】 由框图程序可知12231S k k =+++++++L ，结合循环结构的终止条件可得解 【详解】 由框图程序可知12231S k k =+++++++L 因为11n n n n =+-++，所以213243111S n n n =-+-+-+++-=+-L 所以113S n =+-=，解得15n =，即当15n =时程序退出，故选B ． 【点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.6．如图所示的程序框图，若输出的结果为4，则输入的实数的取值范围是（ ）A ．B ．C ．D ．【答案】A 【解析】，，否，； ，否，； ，否，；，，是，即；解不等式，，且满足，，综上所述，若输出的结果为4，则输入的实数的取值范围是，故选．点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.7．执行如图所示的程序框图，若输入的,,a b c 依次为0.80.9，0.90.8，0.90.9，则输出的x 为（ ）A ．0.80.9B ．0.90.8C ．0.90.9D ．0.80.8【答案】A 【解析】 【分析】根据程序框图知：a 、b 、c 中最大的数用x 表示后输出，比较大小得到答案. 【详解】由题意可知a 、b 、c 中最大的数用x 表示后输出， 若输入的a ，b ，c 依次为0.80.90.90.9,0.8,0.9，利用指数函数的性质可得0.80.90.90.9>，0.90.90.80.9<，故最大的数x 为0.80.9， 故选：A . 【点睛】本题考查了程序框图，理解程序框图表示的意义是解题的关键.8．执行下面程序框图，若输入的的值分别为0和44，则输出的值为（ ）A ．4B ．7C ．10D ．13【答案】C 【解析】 【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值. 【详解】 第一次循环：，，； 第二次循环：，，； 第三次循环：，，；第四次循环：，，刚好满足条件，结束循环，此时输出.故选.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.9．“二进制”来源于我国古代的《易经》，该书中有两类最基本的符号：“—”和“——”，其中“—”在二进制中记作“1”，“——”在二进制中记作“0”，例如二进制数(2)1011化为十进制的计算如下：321(2)(10)10111202121211=⨯+⨯+⨯+⨯=.若从两类符号中任取2个符号进行排列，则得到的二进制数所对应的十进制数大于2的概率为（ ） A ．0 B ．12C ．13D ．14【答案】D 【解析】 【分析】分类计算得到从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3，计算得到概率. 【详解】根据题意，不同符号可分为三类：第一类：由两个“—”组成，其二进制为(2)(10)113=； 第二类：由两个“——”组成，其二进制为(2)(10)000=；第三类：由一个“—”和一个“——”组成，其二进制为(2)(10)102=，(2)(10)011=， 所以从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3， 则得到的二进制数所对应的十进制数大于2的概率14P =， 故选：D. 【点睛】本题考查古典概型及进制转化的应用，意在考查学生的计算能力和应用能力.10．《九章算术》卷第七——盈不足中有如下问题：“今有垣高九尺.瓜生其上，蔓日长七寸. 瓠生其下，蔓日长一尺.问几何日相逢.”翻译为“今有墙高9尺.瓜生在墙的上方，瓜蔓每天向下长7寸.葫芦生在墙的下方，葫芦蔓每天向上长1尺.问需要多少日两蔓相遇.”其中1尺=10寸.为了解决这一问题，设计程序框图如下所示，则输出的k 的值为（ ）A ．8B ．7C ．6D ．5【答案】C 【解析】 【分析】模拟执行程序，依次写出每次循环得到的a,n,S 的值，当S=-1.2时满足条件S 0£ 退出循环输出n 的值从而得解 【详解】运行该程序，第一次，9 1.77.3S =-=，2k =；第二次，7.3 1.7 5.6S =-=，3k =；第三次， 5.6 1.7 3.9S =-=，4k =；第四次， 3.9 1.7 2.2S =-=，5k =；第五次，2.2 1.70.5S =-=，6k =；第六次，0.5 1.7 1.2S =-=-，此时输出的k 的值为6 故选：C 【点睛】本题考查数学文化、算法与程序框图，考查推理论证能力以及化归与转化思想.11．执行如图所示的程序框图，若输入n 的值为13，输出S 的值是46，则a 的取值范围是（ ）A ．910a ≤<B ．910a <≤C ．1011a <≤D ．89a <≤【答案】B 【解析】分析：模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出46S =，即可得到输出条件. 详解：输入13,0n S ==，第一次循环13,12S n ==； 第二次循环25,11S n ==； 第三次循环36,10S n ==； 第四次循环46,9S n ==，输出46S =，此时应满足退出循环的条件， 故a 的取值范围是9010<≤，故选B.点睛：本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.12．《九章算术》是中国古代第一部数学专著，是《算经十书》中最重要的一种，成于公元一世纪左右，它是一本综合性的历史著作，是当时世界上最简练有效的应用数学．“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法，按其算理流程有如下流程框图，若输入的a b 、分别为96、36，则输出的i 为( )A ．4B ．5C ．6D ．7【答案】A 【解析】解：由程序框图可知：当a=96，b=36时，满足a ＞b ，则a=96-36=60，i=1 由a ＞b ，则a=60-36=24，i=2 由a ＜b ，则b=36-24=12，i=3 由a>b ，则b=24-12=12，i=4 由a=b=12，输出i=4． 故选A ．13．运行如图所示的程序框图，设输出的数据构成集合A ，从集合A 中任取一个元素a ，则函数a y x =在(0,)+∞上是增函数的概率为（ ）A ．12B ．35C ．45D ．34【答案】A 【解析】 【分析】按照程序框图运行程序即可得到集合A ，根据幂函数单调性可确定满足条件的a 的所有可能的取值，根据古典概型概率公式计算可得结果. 【详解】按照程序框图运行程序，输入1i =-，满足3i <，则1y =-，0i =，满足3i <； 则0y =，1i =，满足3i <；则3y =，2i =，满足3i <； 则8y =，3i =，不满足3i <，框图运行结束，{}1,0,3,8A ∴=-. 当3a =或8时，a y x =在()0,∞+上是增函数，∴所求概率2142p ==. 故选：A . 【点睛】本题以程序框图和幂函数单调性为载体，考查了古典概型概率问题的求解；关键是能够熟练掌握幂函数的解析式与该函数在第一象限内图象单调性之间的关系.14．如图所示的程序框图是为了求出满足2228n n ->的最小偶数n ，那么在X空白框中填入及最后输出的n 值分别是（ ）A ．1=+n n 和6B ．2=+n n 和6C ．1=+n n 和8D ．2=+n n 和8【答案】D【解析】 空白框中n 依次加2可保证其为偶数，排除A ，C6n =时，622664362628-=-=≤，8n =时，1282282566428-=-> 所以D 选项满足要求．故选：D ．15．德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家､天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n ＝,则输出的结果是( )A ．11114(1)35717P =-+-+⋅⋅⋅+ B ．11114(1)35719P =-+-+⋅⋅⋅- C ．11114(1)35721P =-+-+⋅⋅⋅+ D ．11114(1)35721P =-+-+⋅⋅⋅- 【答案】B【解析】【分析】 执行给定的程序框图，输入10n =，逐次循环，找到计算的规律，即可求解.【详解】由题意，执行给定的程序框图，输入10n =，可得：第1次循环：1,2S i ==；第2次循环：11,33S i =-=；第3次循环：111,435S i =-+=； L L 第10次循环：11111,1135719S i =-+-+-=L ， 此时满足判定条件，输出结果111144(1)35719P S ==-+-+⋅⋅⋅-， 故选：B.【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中认真审题，逐次计算，得到程序框图的计算功能是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.16．执行如图所示的程序框图，若输出的结果为11，则图中的判断条件可以为（ ）A ．1?S >-B ．0?S <C ．–1?S <D ．0?S >【答案】B【解析】【分析】 根据程序框图知当11=i 时，循环终止，此时1lg110S =-<，即可得答案.【详解】1i =，1S =.运行第一次，11lg 1lg30,33S i =+=->=，不成立，运行第二次， 131lg lg 1lg50,535S i =++=->=，不成立，运行第三次， 1351lg lg lg 1lg70,7357S i =+++=->=，不成立，运行第四次， 13571lg lg lg lg 1lg90,93579S i =++++=->=，不成立，运行第五次， 135791lg lg lg lg lg 1lg110,11357911S i =+++++=-<=，成立， 输出i 的值为11，结束.故选：B.【点睛】本题考查补充程序框图判断框的条件，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意模拟程序一步一步执行的求解策略.17．（北京师范大学附中2018届高三下学期第二次模拟）习总书记在十九大报告中指出：坚定文化自信，推动社会主义文化繁荣兴盛．如图，“大衍数列”：0，2，4，8，12来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和．如图是求大衍数列前n 项和的程序框图．执行该程序框图，输入8m =，则输出的S =A ．44B ．68C ．100D ．140【答案】C【解析】第1次运行，211,0,0002n n a S -====+= ，不符合n m ≥ ，继续运行；第2次运行，22,2,0222n n a S ====+= ，不符合n m ≥ ，继续运行；第3次运行，213,4,4262n n a S -====+= ，不符合n m ≥ ，继续运行；第4次运行，24,8,86142n n a S ====+= ，不符合n m ≥ ，继续运行； 第5次运行，215,12,1412262n n a S -====+= ，不符合n m ≥ ，继续运行；第6次运行，26,18,2618442n n a S ====+= ，不符合n m ≥ ，继续运行；第7次运行，217,24,2444682n n a S -====+= ，不符合n m ≥ ，继续运行；第8次运行，28,32,68321002n n a S ====+= ，符合n m ≥ ，推出运行，输出100S = ；故选C18．执行如图所示的程序框图，令()y f x =，若()1f a >，则实数a 的取值范围是（ ）A ．(,2)(2,5]-∞⋃B ．(,1)(1,)-∞-+∞UC ．(,2)(2,)-∞⋃+∞D ．(,1)(1,5]-∞-⋃【答案】D【解析】 分析：先根据程序框图得()f x 解析式，再根据分段函数解三个不等式组，求并集得结果. 详解：因为2,2()=23,251,5x x f x x x x x ⎧⎪≤⎪-<≤⎨⎪⎪>⎩，所以由()1f a >得25225112311a a a a a a >⎧≤<≤⎧⎧⎪⎨⎨⎨>->>⎩⎩⎪⎩或或 所以11225115a a a a a <-<≤<≤∴<-<≤或或或，因此选D.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.19．鸡兔同笼，是中国古代著名的趣味题之一，《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >？B ．94m =？C ．35m =？D ．35m <？【答案】B【解析】【分析】设鸡的数量为i ，兔子数量为j ,则腿的数量共有24m i j =+，判断m 是否为94即可得解.【详解】i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意，35j i =-从0i =开始，依次检验，只需判断足24m i j =+是否为94即可，故框中应填入“94m =？”.故选：B【点睛】本题主要考查了程序框图，循环结构，条件分支结构，属于中档题.20．执行如图所示的程序框图，则输出的S =（ ）A ．5050B ．5151C ．2500D ．2601【答案】C【解析】【分析】 模拟程序的运行，依次写出每次循环得到的S ，i 的值，可得当101i =时，不满足条件100i ≤，退出循环，输出S 的值．【详解】解：模拟程序的运行，可得：1,0,100i S i ==≤，是，0+1=13,100S i i ==≤，，是，1+35,100S i i ==≤，，是，1+3+57,100S i i ==≤，，是，1+3+5+79,100S i i ==≤，，是，L由题可知：当99i =时，100i ≤，是，135799,101,100S i i =+++++=≤L ，否，输出135799S =+++++L ，即()50199505025002S +==⨯=. 故选：C.【点睛】 本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决．。

高考真题理科数学解析汇编：算法初步一、选择题错误!未指定书签。

．（高考（天津理））阅读右边的程序框图,运行相应的程序,当输入x 的值为25-时,输出x 的值为 （ ）A ．1-B ．1C ．3D ．9错误!未指定书签。

．（高考（新课标理））如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则 （ ）A ．AB +为12,,...,n a a a 的和 B ．2A B+为12,,...,n a a a 的算术平均数 C ．A 和B 分别是12,,...,n a a a 中最大的数和最小的数 D ．A 和B 分别是12,,...,n a a a 中最小的数和最大的数开 始 输入x|x|>11||-=x x x = 2x+1 输出x 结 束是否错误!未指定书签。

．（高考（陕西理））右图是用模拟方法估计圆周率π的程序框图,P 表示估计结果,则图中空白框内应填入（ ）A ． 1000NP =B ．41000NP =C ．1000MP =D ．41000MP =错误!未指定书签。

．（高考（山东理））执行下面的程序图,如果输入4a =,那么输出的n 的值为 （ ）A ．2B ．3C ．4D ．5错误!未指定书签。

．（2012年高考（辽宁理））执行如图所示的程序框图,则输出的S的值是（）A．-1 B．23C．32D．4错误!未指定书签。

．（高考（北京理））执行如图所示的程序框图,输出的S值为（）A．2 B．4 C．8 D．16错误!未指定书签。

．（高考（安徽理））如图所示,程序框图(算法流程图)的输出结果是（）A．3B．4C．5D．8k=0,S=1k<3开始结束是否k=k+1输出SS=S×2k（第4题图）二、填空题错误!未指定书签。

．（高考（浙江理））若程序框图如图所示,则该程序运行后输出的值是______________.错误!未指定书签。