八年级下册一次函数动点问题

八下数学能力提升（七）——一次函数动点与四边形综合题班级： 姓名： .学习目标：通过探讨一次函数与四边形综合类问题，引领学生体会分类讨论思想，方程思想，培养学生数学结合能力，图形处理能力，分析问题与解决问题能力。

例题精讲：1.如图，O 为坐标原点，四边形ABCD 是菱形，A （﹣8，8），B 点在第一象限，AB ＝10，AB 与y 轴交于点F ，对角线AC 交y 轴于点E（1）直接写出B 、C 点的坐标；（2）动点P 从C 点出发以每秒2个单位的速度沿折线段C ﹣D ﹣A 运动，设运动时间为t 秒，请用含t 的代数式表示△EDP 的面积；（3）在（2）的条件下，是否存在一点P ，使△APE 沿其一边翻折构成的四边形是菱形？若存在，请直接写出当t 为多少秒时存在符合条件的点P ；若不存在，请说明理由．2.如图，在平面直角坐标系中，直线l ：2343+=x y 与x 轴交于点A ，且经过点B （2，m ），已知点C （3，0）． （1）求直线BC 的函数解析式；（2）在线段BC 上找一点D ，使得△ABO 与△ABD 的面积相等，求出点D 的坐标；（3）y 轴上有一动点P ，直线BC 上有一动点M ，若△APM 是以线段AM 为斜边的等腰直角三角形，求出点M 的坐标；（4）如图2，E 为线段AC 上一点，连结BE ，一动点F 从点B 出发，沿线段BE 以每秒1个单位运动到点E 再沿线段EA 以每秒2个单位运动到A 后停止，设点F 在整个运动过程中所用时间为t ，求t 的最小值．练习：1.如图，直线l 1：y ＝﹣x +b 分别与x 轴、y 轴交于A 、B 两点，与直线l 2：y ＝kx ﹣6交于点C （4，2）（1）求直线l 1和直线l 2的解析式；（2）点E 是射线BC 上一动点，其横坐标为m ，过点E 作EF ∥y 轴，交直线l 2于点F ，若以O 、B 、E 、F 为顶点的四边形是平行四边形，求m 值；（3）若点P 为x 轴上一点，则在平面直角坐标系中是否存在一点Q ，使得以P 、Q 、A 、B 为顶点的四边形是菱形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．2.如图，直线y ＝﹣x +4与x 轴、y 轴分别交于A 、B 两点，直线BC 与x 轴、y 轴分别交于C 、B 两点，连接BC ，且OC ＝43OB ． （1）求点A 的坐标及直线BC 的函数关系式；（2）点M 在x 轴上，连接MB ，当∠MBA +∠CBO ＝45°时，求点M 的坐标；（3）若点P 在x 轴上，平面内是否存在点Q ，使点B 、C 、P 、Q 为顶点的四边形是菱形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．3.如图，已知函数b x y +-=21的图象与x 轴、y 轴分别交于点A 、B ，与函数y ＝x 的图象交于点M ，点M 的横坐标为2，在x 轴上有一点P （a ，0）（其中a ＞2），过点P 作x 轴的垂线，分别交函数b x y +-=21和y ＝x 的图象于点C 、D ．（1）求点A 的坐标；（2）若2OB ＝CD ，求a 的值．（3）填空：若点Q 为平面上任一点，若由A 、O 、D 、Q 组成的四边形是菱形，则Q 点的坐标为 .。

个性化辅导教案
学科数学学生黄芊蕙年级八授课时间2014 年12 月13 日授课教师汪
个性化辅导学案
学科数学学生黄芊蕙年级授课时间2014 年12 月13 日授课教师汪
6、（）如图1，在平面直角坐标系中，已知点(043)A ，
，点B 在x 正半轴上，且30ABO ∠．动点P 在线段AB 上从点A 向点B 以每秒3个单位的速度运动，设运动时间为t 秒．在x 轴上取两点M N ，作等边PMN △．
（1）求直线AB 的解析式；
（2）求等边PMN △的边长（用t 的代数式表示），并求出当等边PMN △的顶点M 运动到与原点O 重合时t 的值；
2. 如右图，在矩形ABCD中，AB=20cm，BC=4cm，点
P从A开始沿折线A—B—C—D以4cm/s的速度运动，点Q从C 开始沿CD边1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达点D时，另一点也随之停止运动，设运动时间为t(s)，t为何值时，四边形APQD也为矩形？
课后作业1.梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从点A开始，沿AD边，以1厘米/秒的速度向点D运动；动点Q从点C开始，沿CB边，以3厘米/秒的速度向B 点运动。

已知P、Q两点分别从A、C同时出发，，当其中一点到达端点时，另一点也随之停止运动。

假设运动时间为t秒，问：
（1）t为何值时，四边形PQCD是平行四边形？
（2）在某个时刻，四边形PQCD可能是菱形吗？为什么？
（3）t为何值时，四边形PQCD是直角梯形？A
D
P
（4）t为何值时，四边形PQCD是等腰梯形？
家长签名。

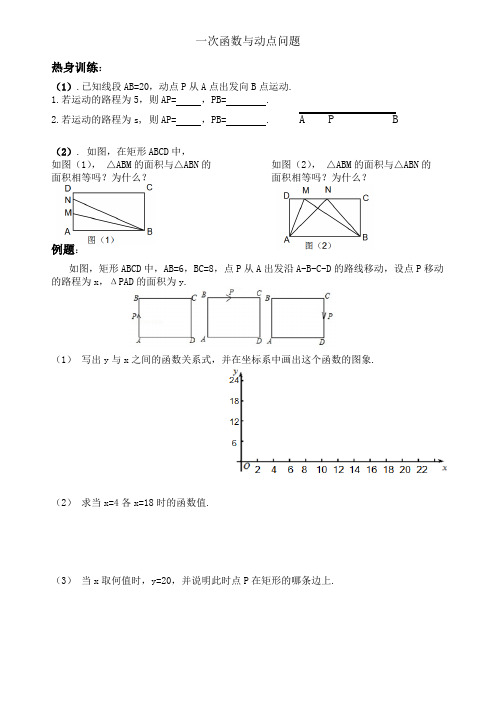
一次函数与动点问题热身训练：（1）.已知线段AB=20，动点P从A点出发向B点运动.1.若运动的路程为5，则AP= ，PB= .2.若运动的路程为s, 则AP= ，PB= . A P B（2）. 如图，在矩形ABCD中，如图（1），△ABM的面积与△ABN的如图（2），△ABM的面积与△ABN的面积相等吗？为什么？面积相等吗？为什么？例题：如图，矩形ABCD中，AB=6，BC=8，点P从A出发沿A-B-C-D的路线移动，设点P移动的路程为x，ΔPAD的面积为y.（1）写出y与x之间的函数关系式，并在坐标系中画出这个函数的图象.（2）求当x=4各x=18时的函数值.（3）当x取何值时，y=20，并说明此时点P在矩形的哪条边上.课堂练习：1.(2016·荆门）如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x(cm)，在下列图像中，能表示△ADP 的面积y(cm)关于x(cm)的函数关系的图像是（）2.如图1，在直角梯形ABCD中，BC为直角腰. 动点P从点B出发，沿BC、CD运动到点D 停止. 设点P运动的路程为x，△ ABP的面积为y. 如果y关于x的函数图象如图2所示，则△BCD的面积是( )A. 3B. 4C. 5D.6作业：正方形ABCD的边长为6cm，动点P从A点出发，在正方形的边上由A→B→C→D运动，设运动的时间为t (s) ，△APD的面积为s (cm2)，s与t的函数图象如图所示，请回答下列问题：(1)点P在AB上运动时间 s，在CD上运动的速度为cm/s, △APD的面积s的最大值为 cm2；(2)求出点P在CD上运动时s与t的函数解析式；(3)当t为 s时，△APD的面积为10cm2.。

八年级数学一次函数动点测试题八年级数学一次函数动点测试题一、选择题1. 下列各组量中，函数关系不是一次函数的是（）。

A．年龄和身高B．年份和总人口数C．面积和直径D．天数和温度2. 一位电工的工资，按照工作时间计算，每小时16元；按照工作量计算，每件30元。

设他这一周工作了h小时，做了j件工作，若他这一周共得到了440元，求出不等式的解集：16h+30j≥440。

（）A．h ≥ 50, j ≥ 1 B．h ≥ 25, j ≥ 10C．h ≥ 10, j ≥ 25 D．h ≥ 1, j ≥ 503. 已知函数y=-2x+5，它的图象和平面直角坐标系的x轴和y轴都有交点，那么下列命题中正确的是（）。

①常数项是5；②斜率是-2；③ x轴上的截距是2.5；④ y轴上的截距是-5。

A．③、④B．①、②C．①、④D．②、③4. 求函数：y=2x+1和y=-0.5x+3的交点坐标。

（）A．(-1, -1)B．(1, 3)C．(-2, -3)D．(2, 5)二、填空题1. 已知函数y=kx+5在点(4,13)处的函数值为29，求k的值为_________。

2. 若在一直线上，函数y=-x+3与函数y=kx+2的图象重合，则k=_________。

3. 已知直线y=kx+b在点(1,3)处的斜率为3，截距为-2，则b=___________。

4. 函数y=kx+b在点(2,5)处为-1，且在点(3,15)处为17，则k=___________。

三、计算题1. 已知函数y=-3x+5，当x=1时，求此函数的函数值，并将其表示出来。

2. 求函数y=4x-8和y=-2x+6的交点坐标，并画出函数的图象。

3. 若已知函数y=kx-2的图象过点(3,7)，求k的值，并求出此函数的解析式。

4. 求函数y=3x-2和y=4x+1的解析式，并求出两函数的交点坐标。

四、综合题1. 以玻璃杯为高度，容积为底积，探究一次函数的性质。

2. 某学生家长打电话给老师，反映他（她）的孩子数学考试考得不够理想，想询问老师孩子在数学中的薄弱知识点。

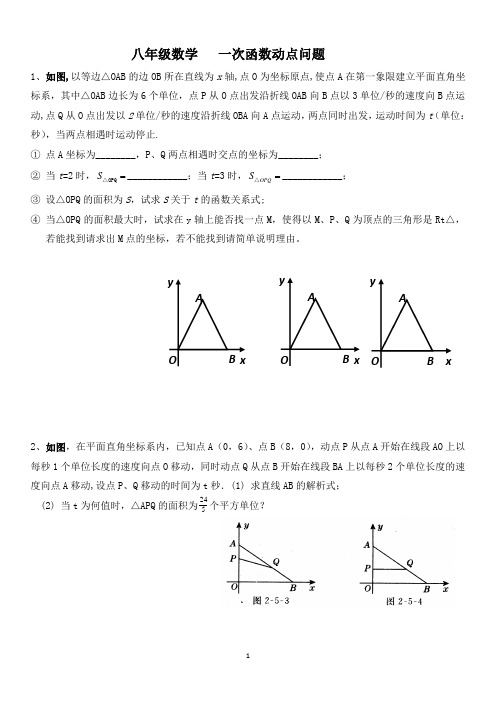
八年级数学 一次函数动点问题1、如图,以等边△OAB 的边OB 所在直线为x 轴,点O 为坐标原点,使点A 在第一象限建立平面直角坐标系，其中△OAB 边长为6个单位，点P 从O 点出发沿折线OAB 向B 点以3单位/秒的速度向B 点运动,点Q 从O 点出发以2单位/秒的速度沿折线OBA 向A 点运动，两点同时出发，运动时间为t （单位：秒），当两点相遇时运动停止.① 点A 坐标为________，P 、Q 两点相遇时交点的坐标为________； ② 当t =2时，S =△OPQ ____________；当t =3时，OPQ S =△____________； ③ 设△OPQ 的面积为S ，试求S 关于t 的函数关系式;④ 当△OPQ 的面积最大时，试求在y 轴上能否找一点M ，使得以M 、P 、Q 为顶点的三角形是Rt △，若能找到请求出M 点的坐标，若不能找到请简单说明理由。

2、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒．(1) 求直线AB 的解析式； (2) 当t 为何值时，△APQ的面积为524个平方单位？xyOAB x yOAB x yOABAFEoyx3、如图，在Rt △AOB 中，∠AOB=90°，OA=3cm ，OB=4cm ，以点O 为坐标原点建立坐标系，设P 、Q 分别为AB 、OB 边上的动点它们同时分别从点A 、O 向B 点匀速运动，速度均为1cm/秒，设P 、Q 移动时间为t （0≤t ≤4）。

（1）过点P 做PM ⊥OA 于M ，求证：AM ：AO=PM ：BO=AP ：AB ，并求出P 点的坐标（用t 表示） （2）求△OPQ 面积S （cm 2），与运动时间t （秒）之间的函数关系式，当t 为何值时，S 有最大值？最大是多少？（3）当t 为何值时，△OPQ 为直角三角形？（4）证明无论t 为何值时，△OPQ 都不可能为正三角形。

例题1：如图，直线1l 的解析表达式为 ，且1l 与x 轴交于点D ，直线2l 经过点A B ，，直线1l ，2l 交于点C ．（1）求点D 的坐标；（2）求直线2l 的解析表达式；（3）求ADC △的面积；（4）在直线2l 上存在异于点C 的另一点P ，使得ADP △与ADC △的面积相等，请直接．．写出点P 的坐标．例题2：如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒．(1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 的面积为个平方单位？当堂巩固：如图，直线 与x 轴、y 轴分别交于点E 、F ，点E 的坐标为（-8，0），点A 的坐标为（-6，0）。

（1）求k 的值；（2）若点P （x ，y ）是第二象限内的直线上的一个动点，在点P 的运动过程中，试写出△OPA 的面积S 与x 的函数关系式，并写出自变量x 的取值范围；（3）探究：当点P 运动到什么位置时，△OPA 的面积为278，并说明理由。

524例题3、如图1，等边△ABC中，BC=6cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度沿AB向终点B移动；点Q以1cm/s的速度沿BC向终点C移动，其中一点到终点，另一点也随之停止．连接PQ，设动点运动时间为x秒．（图2、图3备用）（1）填空：BQ= ，PB= （用含x的代数式表示）；（2）当x为何值时，PQ∥AC？（3）当x为何值时，△PBQ为直角三角形？一次函数压轴题1．如图1，已知直线y=2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第二象限作等腰Rt△ABC 。

（1）求点C的坐标，并求出直线AC的关系式．（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD=AC，求证：BE=DE．（3）如图3，在（1）的条件下，直线AC交x轴于M，P（，k）是线段BC上一点，在线段BM上是否存在一点N，使直线PN平分△BCM的面积？若存在，请求出点N的坐标；若不存在，请说明理由．2．如图直线ℓ：y=kx+6与x轴、y轴分别交于点B、C，点B的坐标是（﹣8，0），点A的坐标为（﹣6，0）（1）求k的值．（2）若P（x，y）是直线ℓ在第二象限内一个动点，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围．（3）当点P运动到什么位置时，△OPA的面积为9，并说明理由．3．如图①，过点（1，5）和（4，2）两点的直线分别与x轴、y轴交于A、B两点．（1）如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．图中阴影部分（不包括边界）所含格点的个数有10个（请直接写出结果）；（2）设点C（4，0），点C关于直线AB的对称点为D，请直接写出点D的坐标（6，2）；（3）如图②，请在直线AB和y轴上分别找一点M、N使△CMN的周长最短，在图②中作出图形，并求出点N的坐标．4．已知如图，直线y=﹣x+4与x轴相交于点A，与直线y=x相交于点P．（1）求点P的坐标；（2）求S△OPA的值；（3）动点E从原点O出发，沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，F的坐标为（a，0），矩形EBOF 与△OPA重叠部分的面积为S．求：S与a之间的函数关系式．5．如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且A点的坐标是（1，0）．（1）直线经过点C，且与x轴交于点E，求四边形AECD的面积；（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；（3）若直线l1经过点F（）且与直线y=3x平行．将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l1于点N，求△NMF的面积．1.考点：一次函数综合题。

一次函数的应用——动点问题题课．学会结合几何图形的性质，在平面直角坐标系中列函数关系式。

1 教学目标．通过对几何图形的探究活动和对例题的分析，感悟探究动点问题列2 函数关系式的方法，提高解决问题的能力。

理解在平面直角坐标系中，动点问题列函数关系式的方法。

重点、难点小结：建立函数模型求解，解要符,用函数知识求解动点问题，需要将问题给合几何图形的性质1 合题意，要注意数与形结合。

函数以及数形结合等思想来研究解决，转化、要充分运用方程、以一次函数为背景的问题，2. 注意自变量的取值范围x经过点，直线轴交于点与，且的解析表达式为如图，直线：1例题211llCB，A ．交于点，，直线21D的坐标；）求点1（ l 的解析表达式；）求直线2（2ADC△面积；的）求3（lC P，使得的另一点上存在异于点）在直线4（2ADC△ADP△P 的坐标．写出点的面积相等，请直接与．．开始A从点P，动点）0，8（B、点）6，0（A如图，在平面直角坐标系内，已知点：2例题上以BA开始在线段B从点Q同时动点移动，O个单位长度的速度向点1上以每秒AO在线段秒．t移动的时间为Q、P设点,移动A个单位长度的速度向点2每秒24 个平方单位？的面积为APQ为何值时，△t当(2) (1) 的解析式；AB求直线5 ]学。

科。

网:来源轴、x与如图，直线当堂巩固：，）0，-8的坐标为（E，点F、E轴分别交于点y 。

）0，-6的坐标为（A点k的值；）求1（y x的运动过程中，试写出P）是第二象限内的直线上的一个动点，在点，（P）若点2（的取值范围；x的函数关系式，并写出自变量x与S的面积OPA△27 ，并说明理由。

的面积为OPA运动到什么位置时，△P）探究：当点3（8 y F E oxA 课后检测：轴上，并x在M点，点B点、A轴分别交于点y轴、x的图象与y=-x+1、如果一次函数1有（M为顶点的三角形是等腰三角形，那么这样的点M、B、A且使以点）。

一次函数动点问题专题练习
1.如图，直线的解析表达式为，且与轴交于点，直线经过点1l 33y
x 1l x D 2l ，直线，交于点．
A B ，1l 2l C （1）求点的坐标；
D （2）求直线的解析表达式；
2l （3）求的面积；
ADC △（4）在直线上存在异于点的另一点，使得
2l C P 与的面积相等，请直接写出点的坐标．
ADP △ADC △P 2.如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点
A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点
B 开始在线段BA 上以每秒2个单位长度的速度向点
A 移动,设点P 、Q 移动的时间为t 秒．
(1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 的面积为
524个平方单
位？[来源:学。

科。

网]。

XX 市XXX 中学统一备课用纸科 目 数学 年级 八 班 级授课时间课 题专题 一次函数中的动点问题课 型新授课教学目标 1、学会结合几何图形的性质，在平面直角坐标系中列函数关系式；2、从变换的角度来研究动点问题中的函数图象，渗透空间观念，培优解决实际问题的能力；3、在解决问题的过程中体会数学思想：数形结合思想、分类讨论思想、方程思想、转化思想.教学重点综合运用一次函数图象中的信息和其它知识解决动点问题教学难点从变换的角度来研究函数图象教具准备多媒体及课件教学内容及过程教学方法和手段一、动点与图形的面积 (校本P106 例2)例1、如图，直线y ＝－x ＋10与x 轴、y 轴分别相交于点B ，C ，点A 的坐标为(8,0)，P(x ，y)是直线 y ＝－x ＋10在第一象限内的一个动点．(1)求△OPA 的面积S 与x 的函数关系式，并写出自变量x 的取值范围； (2)当△OPA 的面积为10时，求点P 的坐标；(3)过点P 作PE ⊥x 轴于点E ，作PF ⊥y 轴于点F ，是否存在一点P ，使得EF 的长最小？若存在，求出EF 的最小值；若不存在，请说明理由．练习：如图，点A 和点B 分别在x 轴和y 轴的正半轴上，OA ＝3，OB ＝2OA ，C 为直线y ＝2x 与直线AB 的交点，点D 的横坐标为1，且在线段OC 上. (1)求点C 的坐标；(2)若P 为线段AD 上一动点(不与点A ，D 重合)．P 的横坐标为x ，△POD 的面积为S ，请求出S 与x 的函数关系式；拓展提升：(3)若F 为直线AB 上一动点，E 为x 轴上一点，是否存在以O ，D ，E ，F 为顶点的四边形是平行四边形？若存在，写出点F 的坐标；若不存在，请说明理由．二、动点与存在性问题(校本P101 变形2)例2：如图，经过点A(6,0)的直线y＝kx－3与直线y＝－x交于点B，点P从点O出发以每秒1个单位长度的速度向点A匀速运动．(1)求点B的坐标；(2)当△OPB是直角三角形时，求运动的时间；(3)当BP平分△OAB的面积时，直线BP与y轴交于点D，求线段BD的长．三、动点与最值问题(校本P106 例1)例3：已知点C(1,0)，直线y＝－x＋7与两坐标轴分别交于A，B两点，D，E分别是线段AB，OA 上的动点(不包括端点)，则△CDE的周长的最小值是.四、课堂小结1、用函数知识求解动点问题，需要将问题结合几何图形的性质，建立函数模型求解，解必须符合题意，注意数与形结合；2、以一次函数为背景的问题，要充分运用方程、转化、函数以及数形结合等思想来研究解决，注意自变量的取值范围.作业布置板书设计教学反思。

一次函数动点问题【例题精讲一】1、如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x 轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；2．如图，直线y=﹣x+4与坐标轴分别交于点A、B，与直线y=x交于点C．在线段OA上，动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动，同时动点P从点A出发向点O做匀速运动，当点P、Q其中一点停止运动时，另一点也停止运动．分别过点P、Q作x轴的垂线，交直线AB、OC于点E、F，连接EF．若运动时间为t 秒，在运动过程中四边形PEFQ总为矩形（点P、Q重合除外）．（1）求点P运动的速度是多少？（2）当t为多少秒时，矩形PEFQ为正方形？3．如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．（1）求C点坐标；（2）求直线MN的解析式；（3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．4、如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标（3，3），将正方形ABCO绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．（1）求证：△AOG△△ADG；（2）求△PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；（3）当△1=△2时，求直线PE的解析式．【例题精讲2】1、如图，四边形OABC是菱形，点C在x轴上，AB交y轴于点H，AC交y轴于点M．已知点A（﹣3，4）．（1）求AO的长；（2）求直线AC的解析式和点M的坐标；（3）点P从点A出发，以每秒2个单位的速度沿折线A﹣B﹣C运动，到达点C终止．设点P的运动时间为t秒，△PMB的面积为S．△求S与t的函数关系式；△求S的最大值．2、如图，点A在y轴上，点B在x轴上，且OA=OB=1，经过原点O的直线l交线段AB于点C，过C作OC的垂线，与直线x=1相交于点P，现将直线L绕O点旋转，使交点C从A向B运动，但C点必须在第一象限内，并记AC的长为t，分析此图后，对下列问题作出探究：（1）当△AOC和△BCP全等时，求出t的值；（2）通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论；（3）△设点P的坐标为（1，b），试写出b关于t的函数关系式和变量t的取值范围．△求出当△PBC为等腰三角形时点P的坐标．3．如图1，在平面直角坐标系中，直线AB与x轴交于点A，与y轴交于点B，与直线OC交于点C．（1）若直线AB解析式为y=﹣2x+12，直线OC解析式为y=x，△求点C的坐标；△求△OAC的面积．（2）如图2，作△AOC的平分线ON，若AB△ON，垂足为E，△OAC的面积为6，且OA=4，P、Q分别为线段OA、OE上的动点，连接AQ与PQ，试探索AQ+PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．4、如图，在平面直角坐标系xOy中，已知直线PA是一次函数y=x+m（m＞0）的图象，直线PB是一次函数y=﹣3x+n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点．（1）用m、n分别表示点A、B、P的坐标及△PAB的度数；（2）若四边形PQOB的面积是，且CQ：AO=1：2，试求点P的坐标，并求出直线PA与PB的函数表达式；（3）在（2）的条件下，是否存在一点D，使以A、B、P、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由．1．阅读下面材料，并解决问题：（I ）如图4，等边△ABC 内有一点P 若点P 到顶点A ，B ，C 的距离分别为3，4，5．则△APB = ，由于P A ，PB 不在一个三角形中，为了解决本题我们可以将△ABP 绕顶点A 旋转到△ACP ′处，此时△ACP ′△ ．这样，就可以利用全等三角形知识，将三条线段的长度转化到一个三角形中从而求出△APB 的度数．（II ）（拓展运用）已知△ABC 三边长a ，b ，c 满足2|62|24144620a c c b -+-++-=．（1）试判断△ABC 的形状 ．（2）如图1，以点A 为原点，AB 所在直线为x 轴建立平面直角坐标系，直接出点B ，C 的坐标 ；（3）如图2，过点C 作△MCN =45°交AB 于点M ，N ．请证明AM 2+BN 2=MN 2；（4）在（3）的条件下，若点N 的坐标是（8，0），则点M 的坐标为 ；此时MN = ．并求直线CM 的解析式．（5）如图3，当点M ，N 分布在点B 异侧时．则（3）中的结论还成立吗？方形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．（1）求G点坐标；（2）求直线EF解析式；（3）点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．3．如图，在平面直角坐标系中，一次函数y=x+2与x轴、y轴交于A、B两点，动点P从A出发沿射线AO运动，动点Q同时从点B出发沿OB的延长线运动，点P、Q的运动速度均为每秒一个单位长．连接PQ交直线AB于D．（1）求A，B两点的坐标；（2）设点P的运动时间为t秒，试求△PBQ的面积S与t的关系式．（3）过P作PE△AB与E，DE的长度是固定值还是不确定的？直接写出你的判断结果不必说明理由．【例题精讲3】1、如图，一次函数的函数图象与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使△ABC=30°．（1）求△ABC的面积；（2）如果在第二象限内有一点P（m，），试用含m的代数式表示△APB的面积，并求当△APB与△ABC面积相等时m的值；（3）是否存在使△QAB是等腰三角形并且在坐标轴上的点Q？若存在，请写出点Q所有可能的坐标；若不存在，请说明理由．2．如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程x2﹣（+1）x+=0的两个根，点C在x轴负半轴上，且AB：AC=1：2（1）求A、C两点的坐标；（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以 A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．【课堂练习】1．如图：直线y=kx+3与x轴、y轴分别交于A、B两点，12OBOA，点C（x，y）是直线y=kx+3上与A、B不重合的动点．（1）求直线y=kx+3的解析式；（2）当点C运动到什么位置时△AOC的面积是6；（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由．2．已知直线y=﹣43x+4与x轴和y轴分别交与B、A两点，另一直线经过点B和点D（11，6）．（1）求AB、BD的长度，并证明△ABD是直角三角形；（2）在x轴上找点C，使△ACD是以AD为底边的等腰三角形，求出C点坐标；（3）一动点P速度为1个单位/秒，沿A﹣﹣B﹣﹣D运动到D点停止，另有一动点Q从D点出发，以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止，两点同时出发，PQ的长度为y（单位长），运动时间为t（秒），求y关于t的函数关系式．3．如图1，在平面直角坐标系中，已知△AOB 是等边三角形，点A 的坐标是（0，4），点B 在第一象限，点P 是x 轴上的一个动点，连接AP ，并把△AOP 绕着点A 按逆时针方向旋转，使边AO 与AB 重合，得到△ABD ．（1）求直线AB 的解析式；（2）当点P 运动到点（3，0）时，求此时DP 的长及点D 的坐标；1、如图，矩形ABCD 的两条边在坐标轴上，点D 与原点重合，对角线BD 所在直线的函数关系式为x y 43=，AD=8，矩形ABCD 沿DB 方向以每秒1个单位长度运动，同时点P 从点A 出发做匀速运动，沿矩形ABCD 的边经过点B 到达点C ，用了14秒。