下载文档原格式
天津大学《最优化方法》复习题(含答案)天津大学《最优化方法》复习题（含答案）第一章 概述(包括凸规划)一、 判断与填空题1 )].([arg )(arg m in m axx f x f nnRx Rx -=∈∈ √2 {}{}.:)(min :)(max nnR D x x f R D x x f ⊆∈-=⊆∈ ⨯3 设.:R R D f n →⊆ 若nR x∈*，对于一切nR x ∈恒有)()(x f x f ≤*，则称*x 为最优化问题)(minx f Dx ∈的全局最优解. ⨯4 设.:R RD f n→⊆ 若Dx∈*，存在*x 的某邻域)(*x N ε，使得对一切)(*∈x N x ε恒有)()(x f x f <*，则称*x 为最优化问题)(minx f Dx ∈的严格局部最优解. ⨯5 给定一个最优化问题，那么它的最优值是一个定值. √6 非空集合nR D ⊆为凸集当且仅当D 中任意两点连线段上任一点属于D . √7 非空集合nR D ⊆为凸集当且仅当D 中任意有限个点的凸组合仍属于D . √8 任意两个凸集的并集为凸集. ⨯ 9 函数RR D f n→⊆:为凸集D 上的凸函数当且仅当f -为D 上的凹函数. √10 设RRD f n→⊆:为凸集D 上的可微凸函数，Dx ∈*.则对D x ∈∀，有).()()()(***-∇≤-x x x f x f x f T⨯ 11 若)(x c 是凹函数，则}0)( {≥∈=x c R x D n是凸集。
√12 设{}kx 为由求解)(minx f Dx ∈的算法A 产生的迭代序列，假设算法A 为下降算法，则对{},2,1,0∈∀k ，恒有)()(1kk x f x f ≤+ .13 算法迭代时的终止准则（写出三种）：_____________________________________。
14 凸规划的全体极小点组成的集合是凸集。
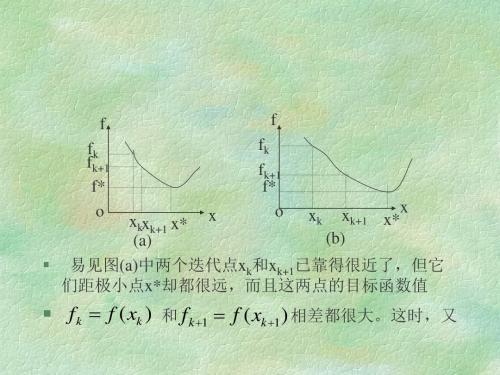
√15 函数RR D f n→⊆:在点kx 沿着迭代方向}0{\n kR d∈进行精确一维线搜索的步长kα，则其搜索公式为 .16 函数RRD f n →⊆:在点kx 沿着迭代方向}0{\n kR d∈进行精确一维线搜索的步长kα，则=+∇k T k k k d d x f )(α 0 .17 设}0{\n kR d∈为点nkR D x⊆∈处关于区域D 的一个下降方向，则对于0>∀α，),0(αα∈∃使得.D d x k k∈+α⨯二、 简述题1 写出Wolfe-Powell 非精确一维线性搜索的公式。
