第四章约束问题的最优化方法解析

[最优化]不等式约束的优化问题求解不等式约束的优化问题求解与前⽂讨论的只含等式约束的优化问题求解类似，含不等式约束的优化问题同样可以⽤拉格朗⽇乘⼦法进⾏求解对于⼀般形式的优化问题：其中，引⼊下⾯两个定义：定义1：对于⼀个不等式约束，如果在处，那么称该不等式约束是处的起作⽤约束；如果在处，那么称该约束是处的不起作⽤约束。

按照惯例，总是把等式约束当作起作⽤的约束定义2：设满⾜，设为起作⽤不等式约束的下标集：如果向量 是线性⽆关的，那么称是⼀个正则点下⾯介绍某个点是局部极⼩点所满⾜的⼀阶必要条件，即KKT 条件。

KKT 条件：设，设是问题的⼀个正则点和局部极⼩点，那么必然存在和，使得以下条件成⽴：那么在求解不等式约束的最优化问题的时候，可以搜索满⾜KKT 条件的点，并将这些点作为极⼩点的候选对象。

⼆阶充分必要条件除了⼀阶的KKT 条件之外，求解这类问题还有⼆阶的充分必要条件。

⼆阶必要条件：在上述的问题中若是极⼩点且。

假设是正则点，那么存在和使得1. 2. 对于所有，都有成⽴⼆阶充分条件：假定，是⼀个可⾏点，存在向量和使得1. 2. 对于所有，都有成⽴那么是优化问题的严格局部极⼩点f(x)subject toh(x)=0g(x)≤0minimize f(x)subject to h(x)=0g(x)≤0f:Rn →R,h:Rn →Rm,m≤n,g:Rn →Rp f :→R,h :→,m ≤n,g :→R n R n R m R n R pgj(x)≤0(x)≤0g j x ∗x ∗gj(x ∗)=0()=0g j x ∗x ∗x ∗x ∗x ∗gj(x ∗)<0()<0g j x ∗x ∗x ∗hi(x)(x)h i x ∗x ∗h(x ∗)=0,g(x ∗)≤0h()=0,g()≤0x ∗x ∗J(x ∗)J()x ∗J(x ∗)≜{j:gj(x ∗)=0}J()≜{j :()=0}x ∗g j x ∗∇hi(x ∗),∇gj(x ∗),1≤i≤m,j ∈J(x ∗)∇(),∇(),1≤i ≤m,j ∈J()h i x ∗g j x ∗x ∗x ∗x ∗f,h,g ∈C1f,h,g ∈C 1x ∗x ∗h(x)=0,g(x)≤0h(x)=0,g(x)≤0λ∗∈Rm ∈λ∗R m µ∗∈Rp ∈µ∗R p Df(x ∗)+λ∗TDh(x ∗)+µ∗TDg(x ∗)=0Tµ∗Tg(x ∗)=0h(x ∗)=0g(x ∗)≤0≥0µ∗Df()+Dh()+Dg()=x ∗λ∗T x ∗µ∗T x ∗0Tg()=0µ∗T x ∗h()=0x ∗g()≤0x ∗x ∗x ∗f,h,g ∈C2f,h,g ∈C 2x ∗x ∗λ∗∈Rm ∈λ∗R m µ∗∈Rp ∈µ∗R p µ∗≥0,Df(x ∗)+λ∗TDh(x ∗)+µ∗TDg(x ∗)=0T,µ∗Tg(x ∗)=0≥0,Df()+Dh()+Dg()=,g()=0µ∗x ∗λ∗T x ∗µ∗T x ∗0T µ∗T x ∗y ∈T(x ∗)y ∈T ()x ∗yTL(x ∗,λ∗,µ∗)y≥0L(,,)y ≥0y T x ∗λ∗µ∗f,h,g ∈C2f,h,g ∈C 2x ∗∈Rn ∈x ∗R n λ∗∈Rm ∈λ∗R m µ∗∈Rp ∈µ∗R p µ∗≥0,Df(x ∗)+λ∗TDh(x ∗)+µ∗TDg(x ∗)=0T,µ∗Tg(x ∗)=0≥0,Df()+Dh()+Dg()=,g()=0µ∗x ∗λ∗T x ∗µ∗T x ∗0T µ∗T x ∗y ∈T~(x ∗,µ∗),y≠0y ∈(,),y ≠0T˜x ∗µ∗yTL(x ∗,λ∗,µ∗)y>0L(,,)y >0y T x ∗λ∗µ∗x ∗x ∗h(x)=0,g(x)≤0h(x)=0,g(x)≤0。

第四章：多维有约束优化方法4.1概述一、多维有约束问题的数学模型机械优化设计问题绝大多数是属于多维有约束非线性规划，其数学模型可表示为式中a i、b i分别为x i的下界和上界。

在求解约束优化问题时，虽然可以利用第三章的无约束优化方法，再加上约束的逻辑判断，使搜索点保持在可行域内逐步逼近约束最优解，但这样处理太复杂，缺乏严格的科学性。

因此，出现了一些直接求解约束优化问题的方法，其基本思路也是数值迭代法。

目前，约束优化方法虽然不如无约束优化方法那样多而完善，但对求解工程优化问题已有很多较好的方法。

二、多维有约束优化方法的分类（1)直接法直接法包括：网格法、分层降维枚举法、复合形法、随机试验法、随机方向法、可变容差法和可行方向法。

(2)间接法间接法包括：罚函数法、内点罚函数法、外点罚函数法、混合罚函数法、精确罚函数法、广义乘子法、广义简约梯度法和约束变尺度法。

直接法不需要利用目标函数和约束函数的梯度，就可直接利用迭代点和目标函数值的信息来构造搜索方向。

间接法要利用目标、约束函数的梯度，其中也包括利用差分来近似梯度的应用。

很多约束优化方法是先转变成无约束优化方法来求解。

可见，无约束优化方法也是也是约束优化方法的基础。

4.2复合形法一、方法概述基本思路：在可行域中选取K个设计点（n+1≤K≤2n）作为初始复合形的顶点。

比较各顶点目标函数值的大小，去掉目标函数值最大的顶点(称最坏点)，以坏点以外其余各点的中心为映射中心，用坏点的映射点替换该点，构成新的复合形顶点。

反复迭代计算，使复合形不断向最优点移动和收缩，直至收缩到复合形的顶点与形心非常接近，且满足迭代精度要求为止。

初始复合形产生的全部K个顶点必须都在可行域内。

二、初始复合形的产生复合形法是一种在可行域内收索最优点大直接解法。

(1)确定可行点作为初始复合形的第一个顶点：式中：通过调整随机数，使第一个初始点控制在可行域范围内。

(2)产生其余（K－1）个随机点。

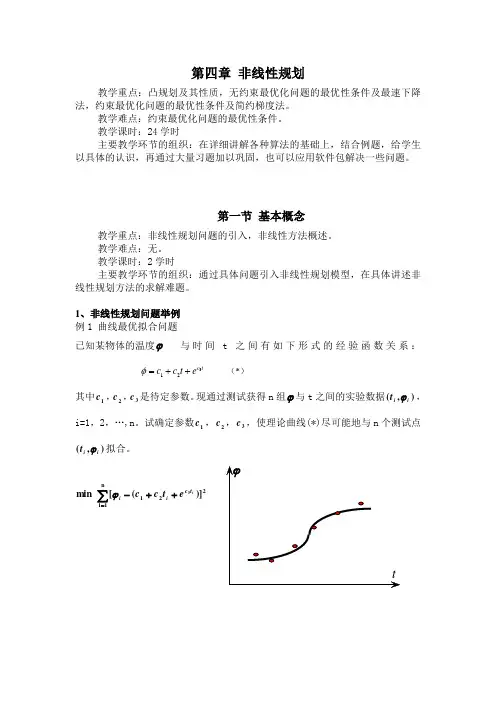
第四章 非线性规划教学重点：凸规划及其性质，无约束最优化问题的最优性条件及最速下降法，约束最优化问题的最优性条件及简约梯度法。

教学难点：约束最优化问题的最优性条件。

教学课时：24学时主要教学环节的组织：在详细讲解各种算法的基础上，结合例题，给学生以具体的认识，再通过大量习题加以巩固，也可以应用软件包解决一些问题。

第一节 基本概念教学重点：非线性规划问题的引入，非线性方法概述。

教学难点：无。

教学课时：2学时主要教学环节的组织：通过具体问题引入非线性规划模型，在具体讲述非线性规划方法的求解难题。

1、非线性规划问题举例例1 曲线最优拟合问题已知某物体的温度ϕ 与时间t 之间有如下形式的经验函数关系：312c t c c t e φ=++ （*）其中1c ，2c ，3c 是待定参数。

现通过测试获得n 组ϕ与t 之间的实验数据),(i i t ϕ，i=1，2，…,n 。

试确定参数1c ，2c ，3c ，使理论曲线(*)尽可能地与n 个测试点),(i i t ϕ拟合。

∑=++-n 1i 221)]([ min 3i t c i i e t c c ϕ例 2 构件容积问题通过分析我们可以得到如下的规划模型：⎪⎪⎩⎪⎪⎨⎧≥≥=++++=0,0 2 ..)3/1( max 212121222211221x x S x x x x a x x t s x x a V ππππ基本概念设n T n R x x x ∈=),...,(1，R R q j x h p i x g x f n j i :,...,1),(;,...,1),();(==,如下的数学模型称为数学规划(Mathematical Programming, MP)：⎪⎩⎪⎨⎧===≤q j x h p i x g t s x f j i ,...,1,0)( ,...,1,0)( ..)( min约束集或可行域X x ∈∀ MP 的可行解或可行点MP 中目标函数和约束函数中至少有一个不是x 的线性函数，称(MP)为非线性规划令 T p x g x g x g ))(),...,(()(1=T p x h x h x h ))(),...,(()(1=，其中，q n p n R R h R R g :,:，那么(MP )可简记为⎪⎩⎪⎨⎧≤≤ 0)( 0 ..)( min x h g(x)t s x f 或者 )(min x f X x ∈ 当p=0,q=0时，称为无约束非线性规划或者无约束最优化问题。

§2.7 约束问题的最优性条件所谓最优性条件就是最优化问题的目标函数与约束函数在最优点处满足的充要条件．这种条件对于最优化算法的终止判定和最优化理论推证都是至关重要的．最优性必要条件是指在最优点处满足哪些条件；充分条件是指满足哪些条件的点是最优点．本节仅讲述最基本的结论．一、约束最优解对约束优化问题的求解，其目的是在由约束条件所规定的可行域D 内，寻求一个目标函数值最小的点*X 及其函数值)(*X f ．这样的解))(,(**X f X 称为约束最优解．约束最优点除了可能落在可行域D 内的情况外，更常常是在约束边界上或等式约束曲面上，因此它的定义及它的一阶必要条件与无约束优化问题不同．（一）约束优化问题的类型约束优化问题根据约束条件类型的不同分为三种，其数学模型如下：（1）不等式约束优化问题（IP 型）min (),..()012i f X s t g X i l ≥=，，，，． （2.16）（2）等式约束优化问题（EP 型）min ()..()012j f X s t h X j m ==，，，，，．（3）一般约束优化问题（GP 型） min ()()012..()012i j f X g X i l s t h X j m ≥=⎧⎪⎨==⎪⎩，，，，，，，，，，．（二）约束优化问题的局部解与全局解按一般约束优化问题，其可行域为 }210)(210)(|{m j X h l i X g X D j i ，，，，；，，，， ===≥=．若对某可行点*X 存在0>ε，当*X 与它邻域的点X 之距离ε<-||||*X X 时，总有)()(*X f X f <则称*X 为该约束优化问题的一个局部最优解．下面以一个简单例子说明．设有⎩⎨⎧=---=≥+=+-=．，，09)2()(02)(..)1()(min 222122221x x X h x X g t s x x X f该问题的几何图形如图2.8所示．从图上的目标函数等值线和不等式约束与等式约束的函数曲线可写出它的两个局部最优解T T X X ]05[]01[*2*1，，，=-=．这是因为在*1X 点邻域的任一满足约束的点X ，都有)()(*1X f X f >；同理，*2X 亦然．１图2.8 对某些约束优化问题，局部解可能有多个．在所有的局部最优解中，目标函数值最小的那个解称为全局最优解．在上例中，由于16)(4)(*2*1==X f X f ，，所以全局最优解为))((*1*1X f X ，． 由此可知，约束优化问题全局解一定是局部解，而局部解不一定是全局解．这与无约束优化问题是相同的．二、约束优化问题局部解的一阶必要条件对于约束，现在进一步阐明起作用约束与不起作用约束的概念．一般的约束优化问题，其约束包含不等式约束l i X g i ，，，， 210)(=≥和等式约束m j X h j ，，，， 210)(==．在可行点k X 处，如果有0)(=k i X g ，则该约束)(X g i 称可行点k X 的起作用约束；而如果有0)(>k i X g ，则该约束)(X g i 称可行点k X 的不起作用约束．对于等式约束0)(=X h j ，显然在任意可行点处的等式约束都是起作用约束． 在某个可行点k X 处，起作用约束在k X 的邻域内起到限制可行域范围的作用，而不起作用约束在k X 处的邻域内就不产生影响．因此，应把注意力集中在起作用约束上．（一）IP 型约束问题的一阶必要条件图2.9所示为具有三个不等式约束的二维最优化问题．图2.9图2.9（a ）是最优点*X 在可行域内部的一种情况．在此种情形下，*X 点的全部约束函数值)(*X g i 均大于零)321(，，=i ，所以这组约束条件对其最优点*X 都不起作用．换句话说，如果除掉全部约束，其最优点也仍是同一个*X 点．因此这种约束优化问题与无约束优化问题是等价的．图2.9（b ）所示的约束最优点*X 在)(1X g 的边界曲线与目标函数等值线的切点处．此时，0)(0)(0)(*3*2*1>>=X g X g X g ，，，所以)(1X g 是起作用约束，而其余的两个是不起作用约束．既然约束最优点*X 是目标函数等值线与)(1X g 边界的切点，则在*X 点处目标函数的梯度)(*X f ∇与约束函数梯度矢量)(*1X g ∇必共线，而且方向一致．若取非负乘子0*1≥λ，则在*X 处存在如下关系0)()(*1*1*=∇-∇X g X f λ．另一种情况如图2.9（c ）所示．当前迭代点k X 在两约束交点上，该点目标函数的梯度矢量)(k X f ∇夹于两约束函数的梯度矢量)()(21k k X g X g ∇∇，之间．显然，在k X 点邻近的可行域内部不存在目标函数值比)(k X f 更小的可行点．因此，点k X 就是约束最优点，记作*X ．由图可知，此时k X 点目标函数的梯度)(k X f ∇可表达为约束函数梯度)(1k X g ∇和)(2k X g ∇的线性组合．若用*X 代替k X 即有)()()(*2*2*1*1*X g X g X f ∇+∇=∇λλ成立，且式中的乘子*1λ和*2λ必为非负．总结以上各种情况，最优解的一阶必要条件为⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≥=∇-∇∑=．，，，，210)(00)()(**21**1*i X g X g X f i i i i λλ 对于（2.16）IP 型约束问题的一阶必要条件讨论如下： 设最优点*X 位于j 个约束边界的汇交处，则这j 个约束条件组成一个起作用的约束集．按上面的分析，对于*X 点必有下式成立⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≥=∇-∇∑=．，，，，，，j i X g X g X f i i j i i i 210)(00)()(**1***λλ （2.17）但是在实际求解过程中，并不能预先知道最优点*X 位于哪一个或哪几个约束边界的汇交处．为此，把l 个约束全部考虑进去，并取不起作用约束的相应乘子为零，则最优解的一阶必要条件应把式（2.17）修改为⎪⎪⎪⎩⎪⎪⎪⎨⎧==≥≥=∇-∇∑=．，，，，，，，l i X g X g X g X f i i iil i i i 210)(0)(00)()(****1***λλλ （2.18）式（2.18）为IP 型问题约束最优解的一阶必要条件，它与式（2.17）等价．因为在*X 下，对于起作用约束，必有l i X g i ，，，， 210)(*==使式（2.18）中的第四式成立；对于不起作用约束，虽然0)(*>X g i 而必有0*=i λ，可见式（2.18）与式（2.17）等价．（二）EP 型约束问题的一阶必要条件图2.10所示为具有一个等式约束条件的二维化问题，其数学模型为．，0)(..)(min =X h t s X f在该问题中，等式约束曲线0)(=X h 是它的可行域，而且目标函数等值线C X f =)(与约束曲线0)(=X h 的切点*X 是该约束问题的最优解．图2.10在*X 点处，目标函数的梯度)(*X f ∇与约束函数的梯度)(*X h ∇共线．因此，在最优点*X 处一定存在一个乘子*u ，使得 0)()(***=∇-∇X h u X f成立．对于一般的n 维等式约束优化问题，其数学模型为min ()..()012j f X s t h X j m ==，，，，，．则*X 为其解的一阶必要条件为***1*()()0()012m j j j j f X u h X h X j m =⎧∇-∇=⎪⎨⎪==⎩∑，，，，，．（三）GP 型约束问题解的一阶必要条件由上述不等式约束优化与等式约束优化问题的一阶必要条件，可以推出一般约束优化问题的条件．设n 维一般约束优化问题的数学模型为⎩⎨⎧===≥，，，，，，，，，，，m j X h l i X g t s X f j i 210)(210)(..)(min （2.19）则*X 为其解的一阶必要条件应为⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧====≥≥=∇-∇-∇∑∑==．，，，，，，，，，，，，m j X h l i X g X g X h u X g X f j i i i i l i m j j j i i 210)(210)(0)(00)()()(*****11*****λλλ （2.20） 函数∑∑==--=l i m j j j i i X h u X g X f u X L 11)()()()(λλ，，称为关于问题（2.19）的广义拉格朗日函数，式中T l ][21λλλλ，，， =，T m u u u u ][21，，， =为拉格朗日乘子．由于引入拉格朗日函数，条件（2.20）中的第一式可写为0)(***=∇u X L X ，，λ．（四）Kuhn —T ｕcker 条件（简称K —T 条件）在优化实用计算中，常常需要判断某可行迭代点k X 是否可作为约束最优点*X 输出而结束迭代，或者对此输出的可行结果进行检查，观察它是否已满足约束最优解的必要条件，这种判断或检验通常借助于T K -条件进行的．对于IP 型问题，T K -条件可叙述如下：如果*X 是一个局部极小点 ，且各梯度矢量)(*X g i ∇组成线性无关的矢量系，那么必存在一组非负乘子*i λ，使得⎪⎩⎪⎨⎧===∇-∇∑=l i X g X g X f ii l i i i ，，，，，210)(0)()(**1***λλ 成立．必须指出，在一般情形下，T K -条件是判别约束极小点的一阶必要条件，但并非充分条件．只是对于凸规划问题，即对于目标函数)(X f 为凸函数，可行域为凸集的最优化问题，T K -条件才是约束最优化问题的充分条件．而且，在这种情况下的局部最优解也必为全局最优解．应用T K -条件检验某迭代点k X 是否为约束最优点的具体作法可按下述步骤进行：（1）检验k X 是否为可行点．为此需要计算k X 处的诸约束函数值)(k i X g ，若是可行点，则l i X g k i ，，，， 210)(=≥． （2）选出可行点k X 处的起作用约束．前面已求得l 个)(k i X g 值，其中等于零或相当接近零的约束就是起作用约束．把这些起作用约束重新编排成序列I i X g i ，，，， 21)(=．（3）计算k X 点目标函数的梯度)(k X f ∇和I 个起作用约束函数的梯度)(k i X g ∇．（4）按T K -条件，k X 点应满足∑==≥=∇-∇Ii i k i i k I i X g X f 1)21(00)()(，，，， λλ. (2.21）将式（2.21）中的各梯度矢量用其分量表示，则可得到i λ为变量的线性方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=∂∂-∂∂-∂∂-∂∂=∂∂-∂∂-∂∂-∂∂=∂∂-∂∂-∂∂-∂∂．，，0)()()()(0)()()()(0)()()()(22112222211211221111n k I I n k n k n k k I I k k k k I I k k k x X g x X g x X g x X f x X g x X g x X g x X f x X g x X g x X g x X f λλλλλλλλλ 由于矢量系I i X g k i ，，，， 21)(=∇是线性无关的，所以该方程组存在唯一解．通过解此线性方程组，求得一组乘子I λλλ，，，21，若所有乘子均为非负，即I i i ，，，， 210=≥λ，则k X 即为约束最优解．否则，k X 点就不是约束最优点．例2.9 设约束优化问题⎪⎩⎪⎨⎧≥=≥=≥--=+-=．，，，0)(0)(01)(..)2()(min 132222112221x X g x X g x x X g t s x x X f 它的当前迭代点为T k X ]01[，=，试用T K -条件判别它是否为约束最优点． 解：（1）计算k X 点的诸约束函数值，，，1)(0)(011)(2221===-=k k k X g X g X gk X 是可行点．（2）k X 点起作用约束是222211)(1)(x X g x x X g =--=，．（3）求k X 点梯度．，，⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=∇⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=∇⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=∇1010)(1212)(022)2(2)()0,1(2)0,1(11)0,1(21k k k X g x X g x x X f（4）求拉格朗日乘子 按T K -条件应有 ．，01012020)()()(212211=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡---⎥⎦⎤⎢⎣⎡-=∇-∇-∇λλλλk k k X g X g X f写成线性方程组 ⎩⎨⎧=-=+-．，0022211λλλ 解得010121>=>=λλ，．乘子均为非负，故T k X ]0,1[=满足约束最优解的一阶必要条件．如图2.11所示，k X 点确为该约束优化问题的局部最优解，由于可行域是凸集，所以点k X 也是该问题的全局最优解．图2.11GP 型的约束最优化问题的T K -条件类似于IP 型约束最优化问题的T K -条件： 如果*X 是一个局部极小点 ，且各梯度矢量)(*X g i ∇和)(*X h j ∇组成线性无关的矢量系，那么必存在两组乘子*i λ和*j u ，使得。