岩石强度理论

应用莫尔—库仑强度理论分析岩石强度摘要：本文介绍了应用莫尔—库仑强度理论来分析岩石强度，该方法具有表达简洁、通俗易懂、使用简单、物理意义清晰等优点，对于分析岩石强度问题具有非常重要的作用。

关键词：库仑强度公式；莫尔应力圆；岩石强度1前言由于岩石成因、矿物成分、成岩环境的多样性，受力状态的复杂多变，岩石的强度特性不容易分析清楚。

准确把握岩石的强度对于工程有着极其重要的作用。

莫尔—库仑强度理论是用来分析岩石抗剪切强度的一种表达简便、使用简单的方法。

2基本思想莫尔—库仑强度理论是在大量试验数据处理、统计分析的基础上得到的。

该理论的基本思想：岩石的剪切破坏并不会发生在只有正应力或者只有剪应力的相对简单的应力条件下，只有在正应力和剪应力同时存在的较复杂的应力条件下才会发生。

只有岩石试件某个截面上作用的剪应力满足岩石的抗剪切强度时，岩石才会沿着该截面发生剪切破坏。

并且莫尔—库仑强度理论假定：岩石的强度只与大、小主应力有关，与中间主应力无关。

岩石的断裂面基本上与中间主应力的作用方向平行。

3库仑强度公式岩石内部各点在荷载作用下将产生应力，为了表述简便清晰，可以将各点任一截面上的应力分解为垂直于截面的正应力和平行于截面的剪应力。

只有岩石试件中一点某截面上作用的剪应力超过岩石的抗剪切强度时，试件才会沿着该截面产生相对滑移，发生滑移破坏。

取成因、矿物成分和成岩环境相同，大小也相同的岩石来模拟岩石剪切破坏。

对岩石上下施加一定的竖直荷载P，然后在岩石左右缓慢施加剪切力，直至岩石上下平行错动，发生剪切破坏，此时剪切力记为S。

若岩石的剪切面面积为A，则剪切面上的正应力为σ=P/A，剪应力为τ=S/A。

分别对不同的岩石施加不同的竖直荷载P，可以得到岩石破坏时不同的剪切力S，进而可以得到σ与τ之间的关系，近似为一直线，用数学公式表示成：τ=σ?tanφ+c,为库仑抗剪强度公式，当中φ称为岩石的内摩擦角， c称为岩石的内聚力。

4平面应力状态下的莫尔应力圆在实际工程中，可以将复杂的空间应力状态简化为平面应力状态（单元体中存在正应力、剪应力均等于零的一对平面）。

第四章岩石的强度岩石强度是岩石的一种重要的力学特性。

是指岩石抵抗载荷（外力）而不受屈服或破裂的能力,是岩石承受外力的极限应力值。

岩石受力后会发生变形，一旦应力达到岩石的极限应力值，岩石就会发生破坏。

在岩石强度应力值之前，存在屈服点(应变明显增大，而应力不再需要明显增大时的应力)，超过屈服点和达到极限强度(岩石破裂要达到的最大应力值)前，一般仍有一些抵抗应变而恢复原形的能力，但达到极限强度后岩石破裂，就完全失去恢复能力。

通常所讲的岩石强度，一般是指岩石样件的测量强度，它仅代表岩体内岩块的强度，不能代表整个岩体的强度。

但在涉及岩石强度的工程问题中，一般是针对岩体的强度，而岩体往往包含一些软弱的结构面。

几组软弱结构面可以将岩体分割成各种形状和大小不同的岩块。

因此，岩体的强度取决于这些岩块强度和结构面的强度，岩块内微结构面的作用将直接反映到岩石的力学性质上。

岩石受力方式的不同，表现出的强度特性不尽相同。

如在张力、压力和剪切力的作用下，同种岩石会呈现出不同的强度特性。

因此岩石具有抗张、抗压和抗剪切强度等之分。

岩石受力条件的不同，可表现出变形、破裂、蠕变等现象，这些现象有着一定的规律性。

岩石的强度是衡量岩石基本力学性质的重要指标，是建立岩石破坏判据的重要指标，还可估计其他力学参数。

岩石的这些力学特性广泛用于建筑行业、水利水电工程、地质灾害研究与预防、断裂构造研究等方面。

4.1影响岩石强度的主要因素1)岩石成分和结构组成岩石的矿物种类及含量、矿物颗粒大小、固结程度、胶结物种类、矿物形态与分布等均影响到岩石的各种强度。

固结程度高、硅质胶结、细粒、交错结构的强度大。

2)岩石中不连续面和间断面岩石中微裂缝、微小断裂、节理层理等的发育程度和分布情况直接影响到岩石的强度，这些不连续或间断面会降低岩石在不同方向上的强度。

3)岩石孔隙度及流体性状岩石的孔隙度以及其中所含流体种类、饱和度、渗透率等因素以较复杂的关系影响着岩石强度。

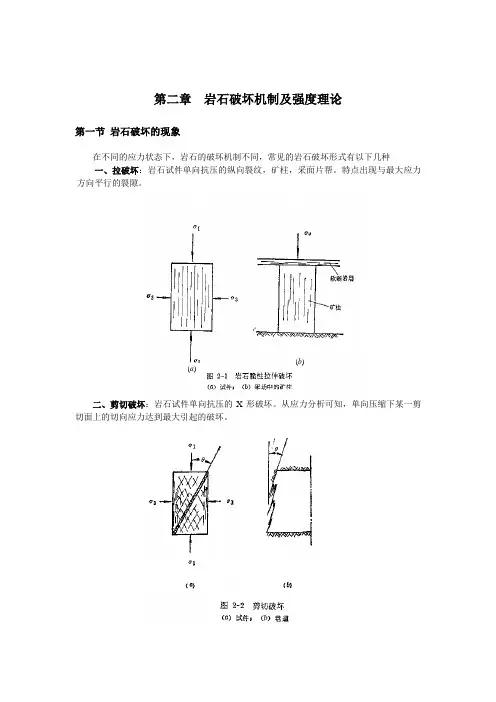
第二章 岩石破坏机制及强度理论第一节 岩石破坏的现象在不同的应力状态下，岩石的破坏机制不同，常见的岩石破坏形式有以下几种一、拉破坏：岩石试件单向抗压的纵向裂纹，矿柱，采面片帮。

特点出现与最大应力方向平行的裂隙。

二、剪切破坏：岩石试件单向抗压的X 形破坏。

从应力分析可知，单向压缩下某一剪切面上的切向应力达到最大引起的破坏。

(a ) (b )三、重剪破坏：即沿原有的结构面的滑动、重剪破坏主要的机制：岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用，侧向压力较小时可能是拉神破坏，实际工程中可能是不同机制的组合，但侧向应力较大时，可以认为剪切应力是岩石重剪破坏的主要破坏机制。

从岩石破坏的现象看，从小到几厘米的岩块到大的工程岩体，破坏形式雷同，并可归纳为两种，拉断与剪坏，因此有一定的规律可寻。

对岩石破坏的研究：在单向条件下可以从实验得到破坏的经验关系。

但是三向受力条件下，不同应力的组合有无穷多种，因此无法仅仅依靠实验得到破坏的经验关系，因此在一般应力状态，对岩石破坏的研究需要结合理论分析和试验研究两个方面。

现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系123(,)f σσσ=研究的方法有：理论分析；2、试验研究；3、理论研究结合试验研究。

第二节 岩石拉伸破坏的强度条件一、最大线应变理论该理论的主要观点是，岩石中某个面上的拉应变达到临界值时破坏，而与所处的应力状态无关。

强度条件为c εε≤ (2-1)c ε—拉应变的极限值，ε—拉应变。

若岩石在破坏之前可看作是弹性体，在受压条件下σ1>σ2>σ3下， 3ε是最小主应力。

按弹性力学有33E Eσμεσσ=-12（+），即33E εσμσσ=-12（+）。

若3ε<0则产生拉应变。

由于E >0，因此产生拉应变的条件是3σμσσ-12（+）<0，3μσσσ12（+）>若3ε=0ε<0则产生拉破坏，此时抗拉强度为0t Eσε＝⇒0t E σε＝。

（一）掌握岩石的物理力学指标及其试验方法；了解岩石的强度特性、变形特性、强度理论；掌握工程岩体分级标准。

1.物理力学指标（物理性质指标）
岩石的容重：单位体积内岩石(包括孔隙体积)的重量称为岩石的容重，单位（N/m³）。

干容重：就是指不含水分状态下的容重。

一般用于表示土的压实效果，干容重越大表示压实效果越好。

最大干容重：是在实验室中得到的最密实状态下的干容重。

密度：单位体积所具有的质量称为密度，公式ρ=m/V(kg/m3);单位体积所具有的重量称为容重，公式γ=G/V（N/m3)，容重等于密度和重力加速度的乘积，即γ=ρg，单位是牛/立方米（N/m³）。

岩石的比重：岩石的比重就是绝对干燥时岩石固体部分实体积(即不包含孔隙的体积)的重量与同体积水(4℃)的重量之比。

单轴压缩试验试件要求：
端部效应是指试样受压时，两端部受其与试验机承压极间摩擦力的束缚、不能自由侧向膨胀而产生的对强度试验值的影响。

渗透系数
2.物理力学指标（变形性质指标）
弹性模量
变形模量
泊松
弹性模量：单位应变的应力。

3.物理力学指标（强度性质指标）
强度指标：抗压强度、抗剪强度、抗剪断强度、抗切强度、抗拉强度
三轴压缩试验：
岩石的强度特性、变形特性、强度
岩石三轴试验要求尽可能地使岩石处于三轴受力情况下
、。

目录1岩石强度、变形及时间效应 (1)1.1 岩石强度和强度准则 (1)1.2 岩石的变形与流变特性 (1)1.2.1岩石的变形 (1)1.2.2岩石流(蠕)变模型 (2)1.2.3岩石的流(蠕)变试验 (3)2岩石断裂与损伤力学 (3)2.1 断裂与损伤机制 (3)2.2 裂纹扩展机制 (4)3岩石多场耦合与应用 (4)3.1 多场耦合关系类型 (5)3.2 多场耦合研究内容与方法 (5)3.3 多场耦合应用 (5)4岩石动力学与岩爆 (6)4.1 岩石动力特性 (6)4.2 岩石动力本构关系 (6)4.3 岩石声、电磁传播特性 (6)4.4 岩爆分析 (7)5岩体非线性理论与加固稳定分析 (8)5.1 岩体非线性理论 (8)5.2 软岩的力学特性与加固理论 (8)5.3 岩质边坡稳定分析 (9)6岩石力学试验技术 (10)6.1 岩石力学基本试验方法 (10)6.2 试验仪器设备 (10)6.3 岩体结构模型试验技术 (10)7岩石力学数值分析方法 (11)7.1 有限元法 (11)7.2 离散元法 (11)7.3 三维快速拉格朗日分析 (12)7.4 数字图像分析方法 (13)8展望岩石力学发展与挑战 (13)参考文献 (15)1岩石强度、变形及时间效应岩石作为自然界的一种天然材料，对其变形和破坏特性的研究是沿着材料力学、弹性力学、塑性力学、断裂力学和损伤力学等逐步发展的。

由于水库大坝、山岭隧道、跨江(海)桥隧等重大工程项目的兴建，以及地下采矿工程、人防工程及地下空间利用的快速发展，促进科技工作者对岩石力学性质与时间效应的持续研究，天然岩石材料的复杂性也越来越为人们所认识。

1.1 岩石强度和强度准则岩石强度理论或强度准则是岩体工程设计、结构安全性分析的基础知识，一直是工程力学界的一个热门课题。

1900年莫尔(O. Mohr)教授建立了著名的莫尔-库仑(Mohr-Coulomb)强度理论。

从那以后，岩石强度理论广泛吸引了工程师和物理学家(包括工程地质专家、力学家、地球物理学家、材料科学家和土木、机械工程师等)的注意。

岩石材料的强度理论总结屈服准则又称塑性条件，它是描述不同应力状态下物体某点进入塑性状态并使塑性变形继续进行所必须满足的条件。

一般来说，材料的屈服准则可分为三类：(1)应力表示的屈服准则；(2)应变表示的屈服准则；(3)能量表示的屈服准则。

在传统塑性理论中，最早应用的是1864年由屈瑞斯卡(Tresca)提出的屈瑞斯卡屈服准则，它适用于金属材料。

关于岩石的强度准则，最初是引用金属和土体的强度准则，后来发现岩石抗拉强度和抗压强度相差很大，静水压力的大小影响岩石材料脆塑性破坏等性质，这些金属和土体的准则不适合岩石材料。

几百年来各国学者提出了很多个岩石强度准则，但没有一个强度准则能够被所有人接受。

其中Mohr －Coulomb 强度准则，Drucker-Prager 强度准则，双剪统一强度理论和Hoek-Brown 强度准则在岩石力学中具有较大的影响。

1. Tresca 准则该准侧主要针对的是金属类材料和φ=0的纯黏土分析，又称最大剪应力屈服准则，即，当材料的最大剪应力达到某一极限值T k 时，材料产生屈服，其函数表示为：222222122331()4()4()40T T T f k k k σσσσσσ⎡⎤⎡⎤⎡⎤=--⋅--⋅--=⎣⎦⎣⎦⎣⎦(1) k T 为Tresca 准则材料常数，由实验测定。

当进行单向压缩实验时，σ2=σ3=0，σ1=σs ，得k T =12σs ⁄；当进行纯剪切实验时，σ2=0，σ3=−σ1=τs ，则k T =τs 。

在主应力空间中，Tresca 准则的屈服面是一个以静水压力线或空间对角线为轴的正六角柱体，在偏平面上是一个六边形，而在σ2=0的平面内则是一个具有两个直角的正六边形。

在p-q 平面为两条平行于p 轴的直线，说明Tresca 准则与静水压力无关。

2. Mises 准则Mises 准则是针对Tresca 准则没有考虑σ2对屈服的影响以及屈服面有棱角的缺陷，在对金属材料的实验分析基础上，同时考虑三个主应力影响的屈服准则，它考虑了材料的形状变化能，即当材料的形状变化比能达到一定程度时，材料开始屈服，故又称能量屈服准则。